经历实验探索过程,积累基本活动经验
——以《圆锥的体积》一课的教学为例
□张冬萍
从《义务教育数学课程标准(2011 年版)》到《义务教育数学课程标准(2022 年版)》,课程总目标都强调:“获得适应未来生活和进一步发展所必需的数学基础知识、基本技能、基本思想、基本活动经验。”其中“基本活动经验”的要求,进一步丰富了数学教育的内涵。所谓“基本活动经验”就是在数学目标的指引下,通过对具体的事物进行实际操作、考察和思考,从感性向理性飞跃时所形成的认识(张奠宙,2008)。基本活动经验的积累过程是学生主动探索的过程。学生有了这样的基本活动经验,可以加深对数学知识的理解,发展创新意识,提高综合运用能力。
在现行的小学数学教材中,有不少的教学内容需要学生经历这种实验探究过程,以实现积累“基本活动经验”的目标。如在《圆锥的体积》公式推导教学中,教师通常会带领学生简单开展操作、验证的活动,即用圆锥装沙三次,倒入与它等底等高的圆柱中,正好装满,所以圆锥体积等于与它等底等高圆柱体积的三分之一。这样的教学存在以下问题。
问题一:圆锥体积的大小究竟与哪些因素有关?学生并不清楚,只是简单套用公式。
问题二:为什么要“等底等高”,学生并不理解,只能硬记。
问题三:从实验研究角度看,没有体现“因变量”与“自变量”之间的关系,缺乏过程体验,缺乏用多种路径来推导体积计算方法,影响学生探究能力、应用能力的发展。
在小学数学实验教学中,如何让学生经历实验探究过程呢?下面以《圆锥的体积》公式推导为例,谈一谈实验教学的过程及其教学要点。
一、在猜想、观察、比较中,体会影响圆锥体积大小的因素
通过“观察—猜想—比较”的学习过程,将两组不同的对象进行比较,发现圆锥体积与高、底面积两个因素有关。
【教学片段】
师(出示各种大小不一的圆锥):圆锥的体积有大有小,请大家猜想一下,圆锥体积的大小与什么有关?(生答)
师:观察下列各组圆锥(分组出示),它们之间有什么联系?每组中的圆锥哪个体积大?哪个体积小?圆锥体积的大小与什么因素有关?(如图1、图2)
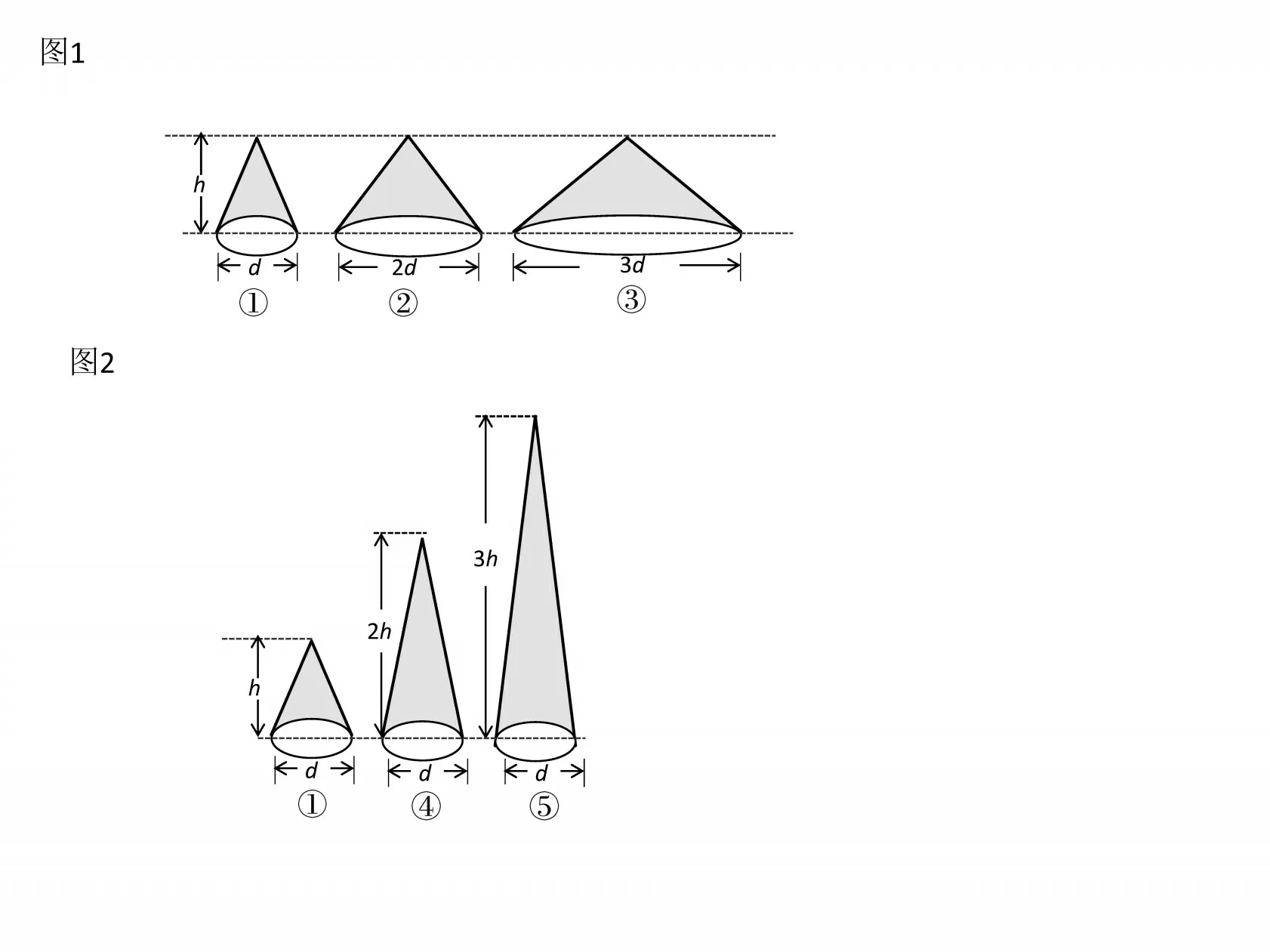
图1
学生通过观察、比较,发现第1组(如图1)中的三个圆锥,它们的高相等,底面积大小不同,底面积越大,体积也越大,从中体会圆锥体积的大小与底面积大小有关。通过观察、比较第2 组(如图2)中的三个圆锥,它们的底面积大小相同,高不同,高越长,圆锥的体积也越大,进一步体会到圆锥体积的大小与它的高有关。通过这样的观察、比较,学生自主发现影响圆锥体积大小的因素是底面积与高。
【教学思考】
通过“高相等底不等”“底相等高不等”两组圆锥实物的观察、比较,学生能自主发现影响圆锥体积大小的因素是圆锥的底与高,为后续研究“圆锥的体积与它的底、高有什么关系”“为什么要等底等高”打下基础。同时在这一过程中,通过控制两个变量,进一步掌握实验探究的基本方法,提高实验探究的技能。
二、在实验、交流、讨论中,理解体积计算方法
学生通过选择不同的实验,发现虽然过程各不相同,但得到的结论是一样的。在交流、讨论中感悟推导的道理。
【教学片段】
1.引导实验,运用实验结果推导计算方法
圆锥底面积大小、高的长短是决定体积大小的因素,那么它们之间有什么关系呢?或者说怎样通过底面积、高求出圆锥的体积呢?教师请每个小组选择5 个圆锥中的一个或几个,以及对应圆柱,通过实验的方法推导出圆锥体积计算的公式。
实验提示:(1)把你所选的圆锥底面半径看作r,圆锥高看作h,对应比较的圆柱,圆柱的底面半径用含有r 的式子表示,圆柱的高用含有h 的式子表示。
(2)这5个圆锥体积计算方法推导的难度是不同的。
☆:①号 ☆☆:③⑤号 ☆☆☆:②④号
(3)在所选的圆锥中装满沙子,再倒入圆柱体中,根据倒的次数,推导出圆锥体积计算公式。
学生实验推导过程与方法。
方法1:用①号圆锥装满沙子,倒入圆柱容器,正好三次注满。通过实验发现,所选圆锥体积是这个圆柱体积的三分之一,所选的圆锥与圆柱正好是等底等高(如图3)。
图2
方法2:用③号圆锥装满沙子,倒入圆柱容器,正好可以注满3 个圆柱容器。所选圆锥是这个圆柱体积的3倍(如图4)。
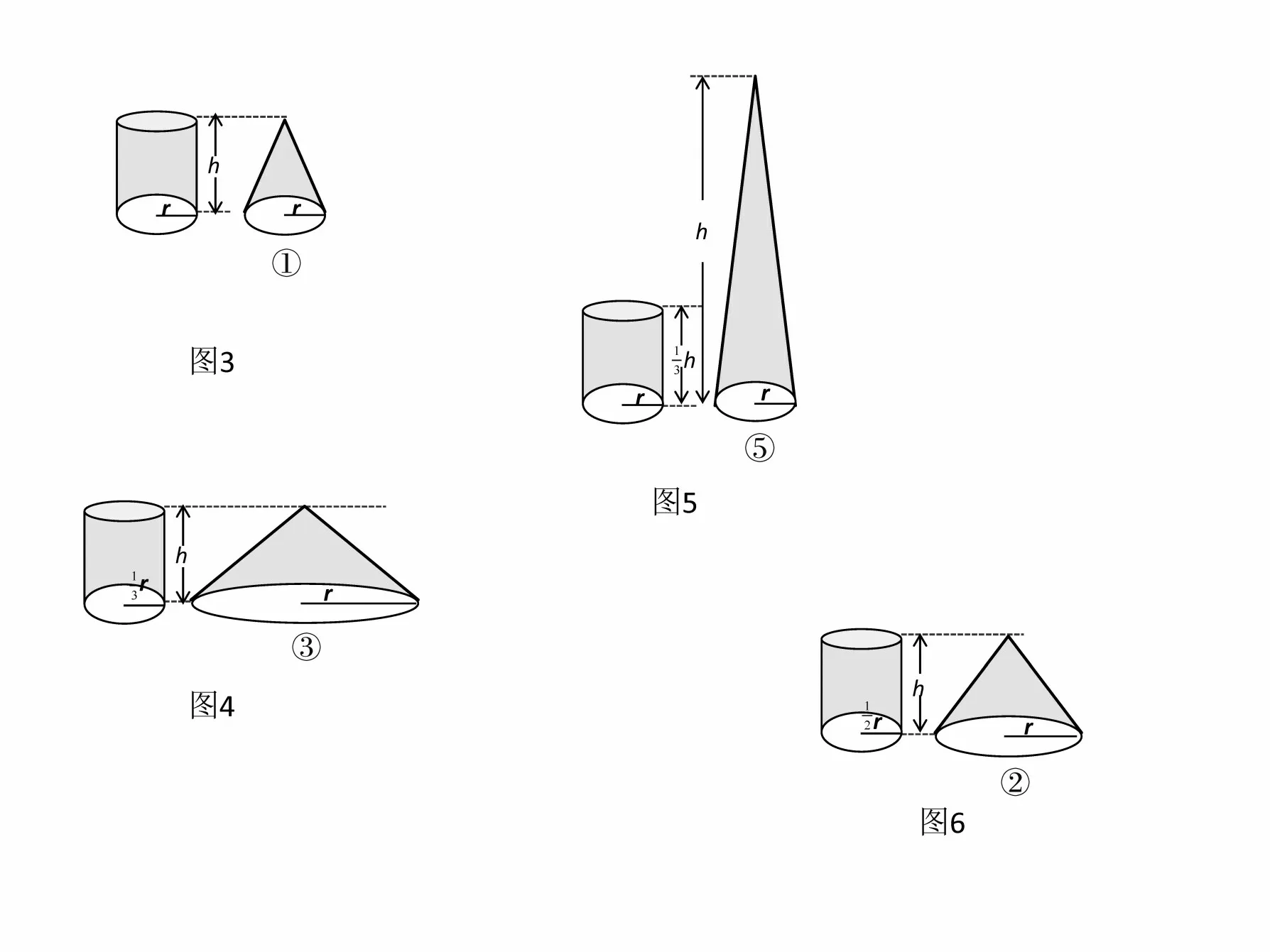
图3
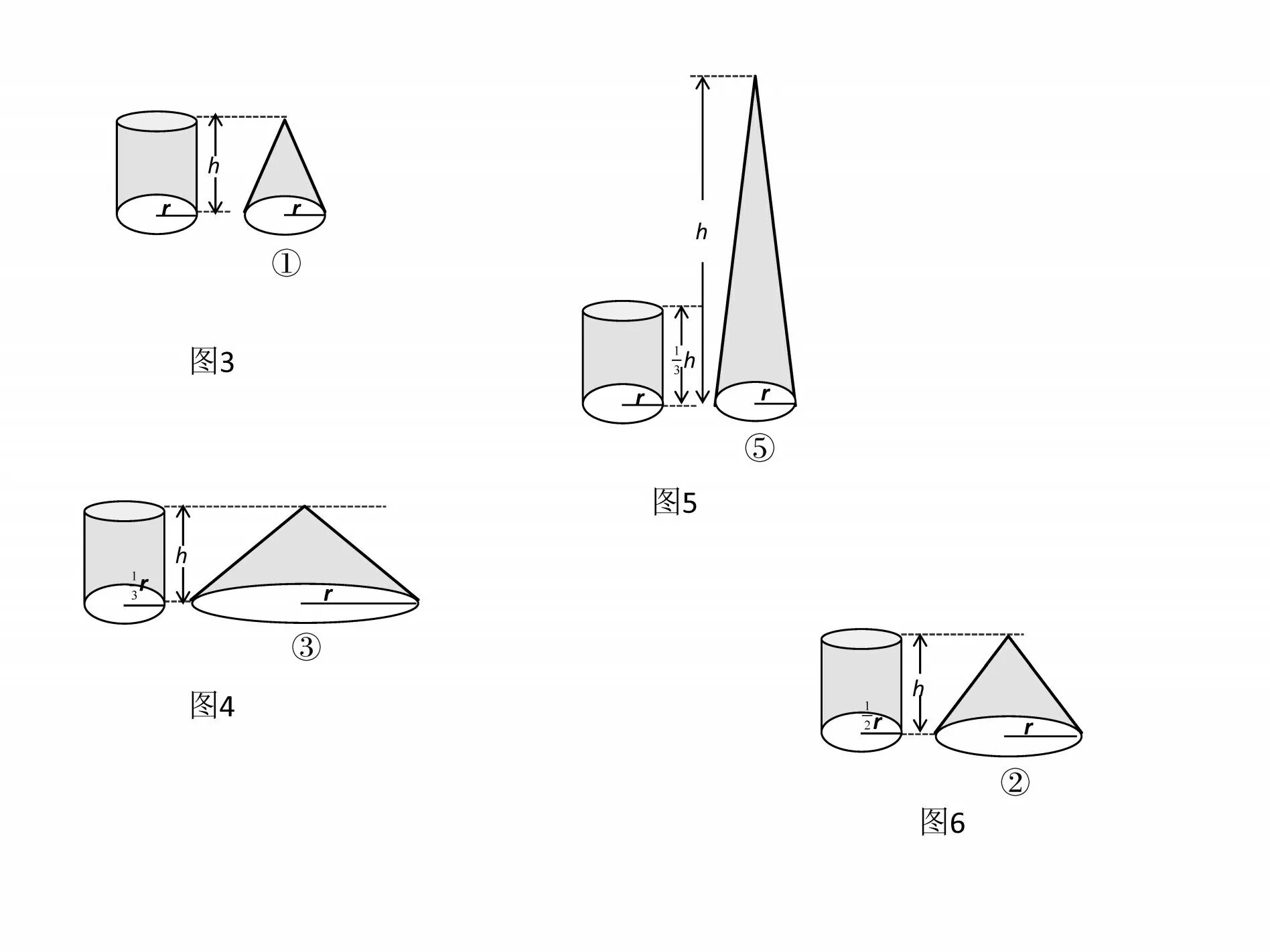
图4
方法3:用⑤号圆锥装满沙子,倒入圆柱容器,正好一次就将圆柱注满。所选圆锥的体积正好是这个圆柱的体积(如图5)。
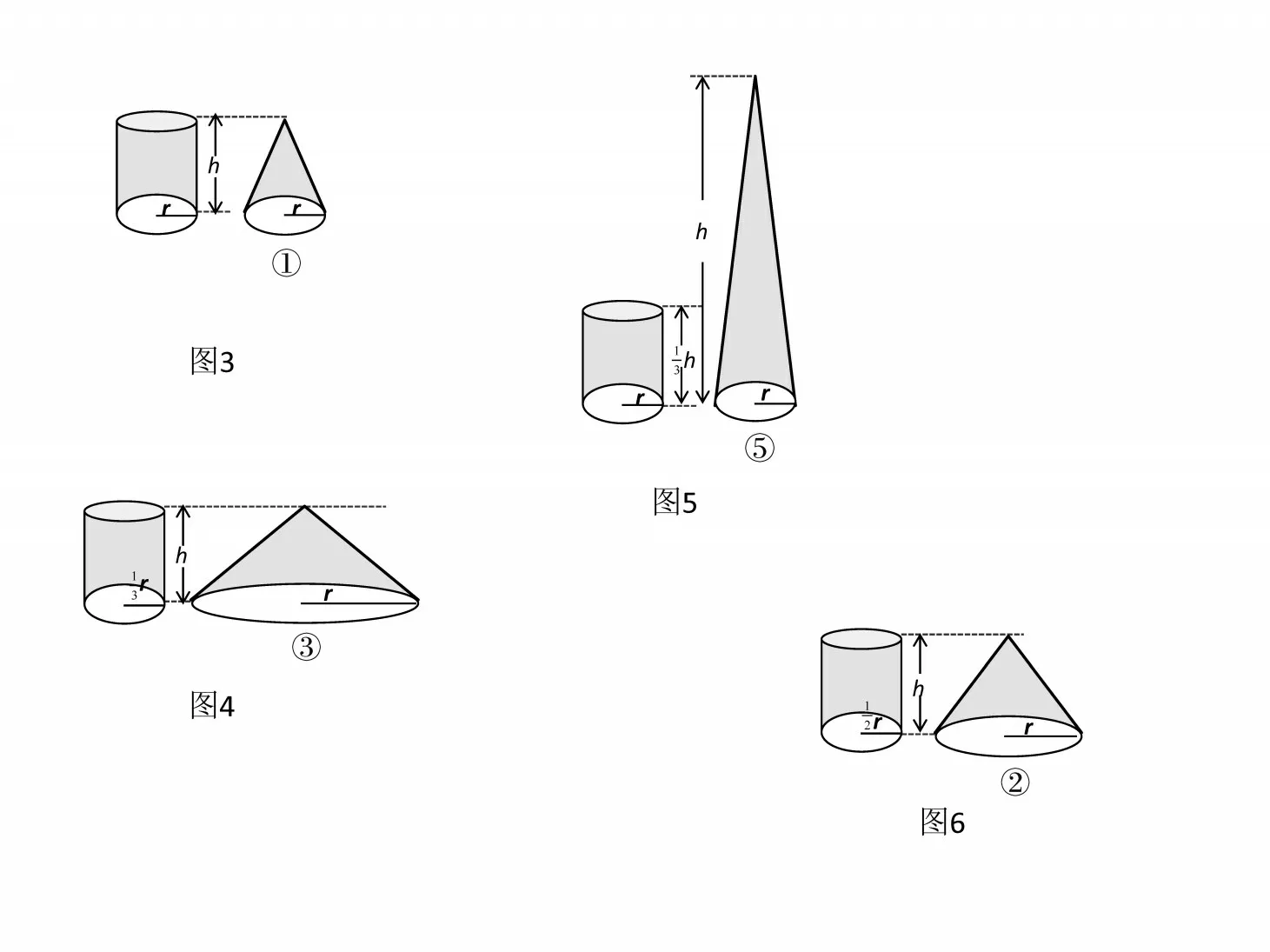
图5
方法5:用④号圆锥装满沙子,倒入圆柱容器,一次能注满圆柱容器的,或者3 次能注满2 个圆柱容器。所选圆锥的体积是这个圆柱体积的(如图7)。
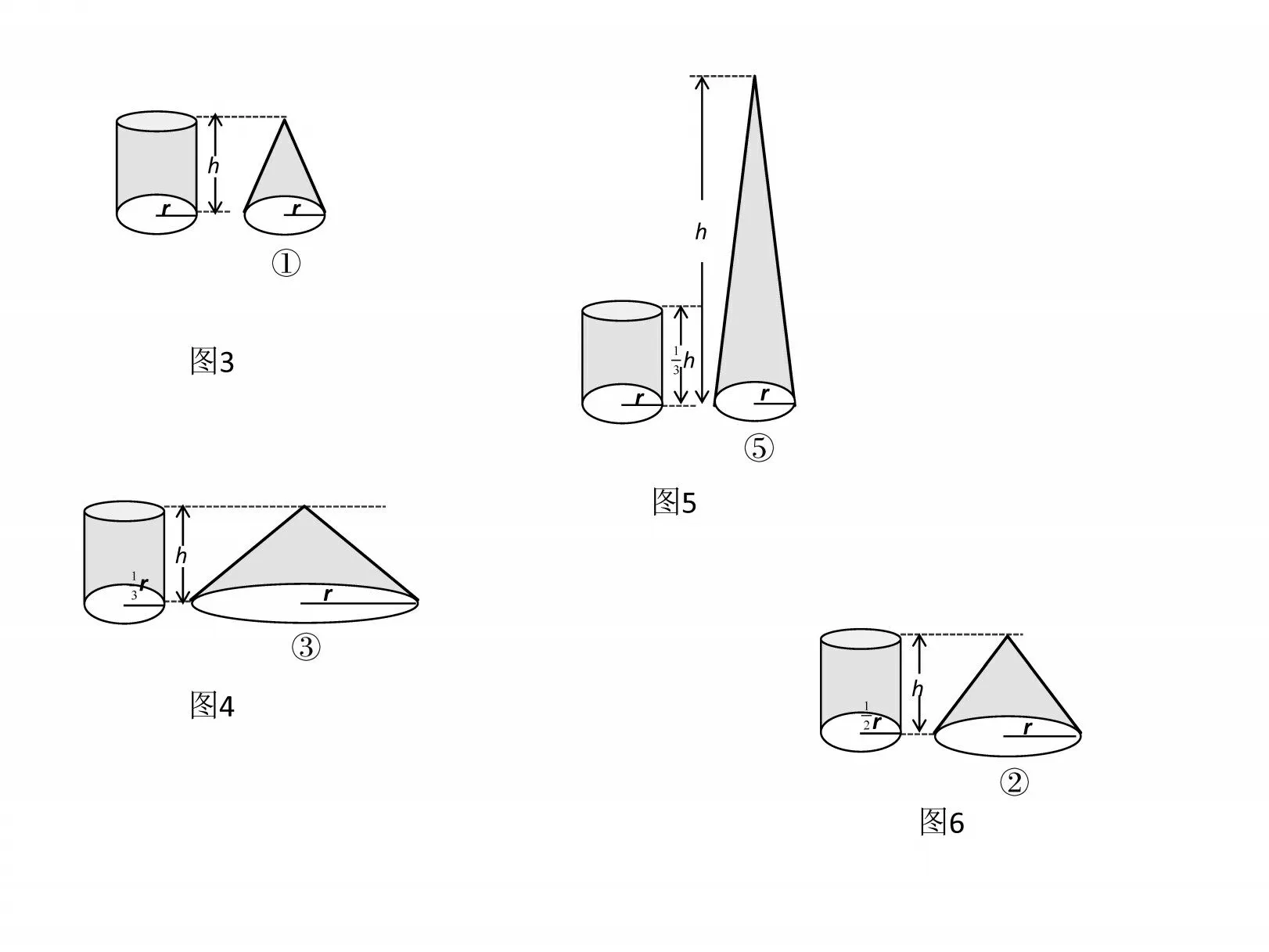
图6

图7
关系表示
2.反馈交流中讨论
在学生的反馈交流中,教师适时追问:“画框部分是依据什么得到的?”使得学生进一步明确依据实验结果进行推导的道理。
最后归纳得出:圆锥体积等于与它等底等高圆柱体积的三分之一。
【教学思考】
1.星级导学,激发学生的实验探究热情
用5 组不同的圆锥来推导体积计算方法,难度各不相同,其中用①号图推导最简单,也是最基本的,②④号最难。不同难度层次的实验探究材料,能满足不同认知水平学生的需求。笔者在一次教学实践中,将全班分成10 个四人小组,让学生自主选择实验探究材料,有5 组学生选用①号图,3 组学生选用③号图或⑤号图,有2 组学生运用②号图或④号图,每个组都推导出圆锥体积计算公式,其中有一个组在选用①号图完成任务后,又用④号图实验推导出计算公式。每个组都经历了实验、推导的过程,使不同的学生有不同的发展,并通过交流反馈,共享其他组的研究成果,开阔了学生探究视野。
2.架设脚手架,为学生顺利探究铺路
三条实验探究的提示语,尤其是第一条“把你选的圆锥底面半径看作r,圆锥高看作h,对应比较的圆柱,圆柱的底面半径用含有r的式子、表示圆柱的高用含有h的式子表示。”利用这样的提示,学生可以减少实验探究的盲目性,能成功地推导出体积计算公式,使得实验探究过程更有效。
3.实验过程交流,开拓学生探究视野
通过实验探究过程的反馈交流,学生不仅展示了自己的研究成果,获得了成功的喜悦,而且在聆听其他同学的研究成果中,感悟到解决同一问题可以用不同的方式,真是“条条大路通罗马”。无论用哪种方式,在推导计算方法时都要依据实验结果,并与底面积、高建立联系,进而推导出圆锥体积计算公式。
4.适时讨论,加深对圆锥与圆柱关系的理解
在学生反馈中,教师追问“画框部分是依据什么得到的”,使得学生进一步明确依据实验结果进行推导的道理,并依据实验结果,将体积与底面半径、高建立联系,进而得到圆锥体积的计算公式。
在对“这个公式中的πr2h 表示的是什么”并结合图式进行解释的过程中,学生认识到每一种推导方法中的“πr2h”都是对应的与所选的圆锥等底等高的圆柱体积,加深了对“等底等高”必要性的理解。
三、反思过程与方法,感悟数学思想,提高解决问题能力
实验探究活动结束后,教师应及时引导学生对探究过程、探究方法进行梳理。学生能在反思过程中,积累基本活动经验,感悟数学思想。
【教学片段】
师:想一想,刚才是如何运用实验探究推导出圆锥体积的计算公式的?
生:猜想圆锥体积大小与什么有关,观察实物,验证猜想。
生:通过倒沙子实验操作,看一看所选的圆锥要几次才能把圆柱容器注满。
生:用实验结果来推导出计算公式。
师:在推导圆锥体积计算公式时,要借助于什么物体来推导?
生:圆柱体。
师:推导圆锥体积公式我们都借助于圆柱,圆柱体积是我们已学的、已知的,把未知的圆锥转化为已知的圆柱来找到计算体积的方法,这是我们数学中常用的思维方式——化归思想,就是把新的内容转化为已经学过的内容。在以后的学习中如果遇到新的内容无法解决时,就可以试着转化为以前学过的内容,这样往往就可以找到解决问题的途径。
【教学思考】
在实验探究教学中,有不少教师认为,当要探究的问题得到解决后,探究过程也就结束了,紧接着的就是应用探究结果解决问题。殊不知,对探究过程、探究方法的反思是积累基本活动经验的重要途径。本课中,当学生得出结论后,教师引导学生反思“想一想,刚才是如何运用实验方法推导出圆锥体积的计算公式的”,通过梳理探究过程与方法,让学生进一步体会到探究中常常要对探究对象作出猜想,要通过实验、推理、验证等思维过程,判断猜想是否正确,要依据实验结果推导计算公式,运用化归思想将未知的转化为已知的,新内容转化为已学内容。对于学生而言,经历了这些过程,获得了一些实验的经验,通过反思,逐渐积淀了一些比知识更为重要的数学思想,对今后的学习、工作都能起到积极的作用。
经验来自于经历,在实验探究教学中,教师应多设计一些让学生亲身经历探究过程的环节,学生在猜想、验证、推理、交流中积累数学的基本活动经验,在教师追问中引发学生讨论,充分理解数学的知识与方法,在引导反思探究过程中掌握一些基本的数学思想,坚持这样做,“四基”的目标要求才能落到实处,才能真正发展学生解决问题的能力。


