融合项目质量与时间的矩阵分解协同过滤算法

邵 超，崔丽莎

（河南财经政法大学计算机与信息工程学院，河南郑州 450046）

0 引言

20 世纪90 年代以来，随着互联网和信息技术的快速发展，信息量呈现爆炸式增长，人们面对浩如烟海的信息无所适从。针对“信息超载”问题，个性化推荐系统能够“主动”推荐用户感兴趣的信息和资源，并已在电子商务［1］、视频音乐推荐［2］等领域广泛应用。现阶段，传统推荐算法主要包括基于关联规则的推荐（Association Rules Based）［3］、基于内容的推荐（Content Based）［4］、协同过滤推荐（Collaborate Filtering）［5］等。其中，协同过滤推荐算法是目前应用最广泛的推荐技术。

协同过滤推荐又分为基于内存（Memory-Based）、基于模型（Model-Based）和混合（Hybrid-CF）的协同过滤推荐。其中，基于内存的协同过滤推荐通过用户历史行为数据挖掘用户偏好，寻找存在共同经验的群体推荐用户感兴趣的项目，在此基础上又可细分为基于用户和基于项目两类。然而该方法存在数据稀疏、冷启动、用户兴趣迁移等问题。随后，提出了基于模型的协同过滤推荐，该算法在协同过滤推荐的基础上，利用机器学习思想建立各类模型进行推荐，例如聚类［6］、分类［7］、矩阵分解［8］、神经网络［9］等。相较于前者，该类方法推荐效果更佳，混合协同过滤推荐则主要通过融合以上两种方法进行推荐。

目前，改进协同过滤算法主要通过挖掘用户的潜在偏好，改进相似度计算，优化最近邻选择以提升推荐质量。何明等［10］结合用户评分和项目类型信息构建用户兴趣偏好矩阵，基于此对用户进行聚类。王卫红等［11］引入用户对项目类型的平均评分和用户属性构建用户偏好，将其填充后对用户进行聚类。李志军［12］引入评分比例因子和商品属性改进项目相似度计算，结合用户评分构建用户对商品的喜好矩阵。以上研究均根据用户评分和项目类型信息构建用户偏好，有助于缓解数据稀疏性，提高推荐效果。然而，此类研究并未在产生候选集时考虑用户对项目类型的偏好，忽略了用户评分越早对用户当前偏好的反映程度越低的兴趣迁移问题。文献［13-14］通过引入时间权重因子分别改进了用户评分相似度与物品相似度度量公式，却未在构建用户偏好时考虑时间因素的影响。陆航等［15］引入时间衰减函数到标签权重计算中，却忽视了用户评分对用户偏好的反映程度。文献［15-16］考虑了项目质量对用户评分存在的影响，分别将项目质量作为差异影响因子与惩罚因子，优化计算用户评分差异相似度与改进相似度计算公式。然而，该类研究仅将项目质量应用于改进相似度计算中，忽略了项目质量可通过影响用户评分而影响挖掘用户偏好。

此外，由于矩阵分解具有良好的可扩展性和评分预测准确性，有助于缓解数据稀疏，故而得到广泛关注并产生了多种变体。马莹雪等［17-18］通过神经网络学习目标用户和项目的特征向量，将其集成在矩阵分解模型上产生预测评分。王运等［19-20］利用用户属性信息和项目标签信息获取用户相似度和项目相似度，将其融入PMF 模型中实现推荐。Luo 等［21］探寻标签与项目的关联，并在矩阵分解中添加时间影响因子优化用户偏好，取得了良好效果。然而，这些算法仍存在以下不足：①神经网络模型复杂且对数据具有依赖性；②仅考虑用户和项目的属性信息，忽略了用户的兴趣迁移；③未考虑项目自身质量对评分的影响。

为解决上述问题，本文提出了一种融合时间因素、项目质量及项目类型信息的矩阵分解协同过滤算法，首先引入项目评分标准差作为衡量项目质量对用户评分影响程度的质量因子，消除由项目自身质量产生的评分误差，并引入时间权重因子反映用户兴趣的动态变化；然后，结合修正的用户评分和项目类型信息获取用户当前的项目类型偏好，以此产生推荐候选集；最后，基于修正后的用户——项目评分，采用矩阵分解预测用户对候选集中的项目进行评分，将评分最高的N个项目推荐给用户。

本文的主要贡献有以下3 个方面：①在用户项目类型偏好构建和评分预测中引入项目评分标准差，作为衡量影响程度的质量因子；②在用户——项目类型兴趣度计算中引入时间权重因子，以获取用户当前的项目类型偏好；③在候选集生成过程中考虑了用户当前项目类型偏好，以此优化候选集。

1 相关概念

1.1 相关定义

项目质量：项目自身的质量属性。以电影为例，当拍摄质量较高时，通常会导致观众无论是否喜欢该类型的电影，都会评于高分。

时间因素：用户的兴趣并非一成不变，而是随着时间呈动态变化。

用户对项目类型的偏好：以电影为例，电影具有多种类型。例如，喜剧、动作片等，而用户对各种类型的偏好不尽相同。

1.2 用户兴趣变化

传统协同过滤算法假定用户的兴趣是固定的，不会随着时间的推移而动态变化，因此将用户所有的历史行为看作同等影响力，以此计算用户偏好和寻找最近邻，推荐与目标用户偏好相似的项目。然而，这种假定在现实生活中并不成立，人们的兴趣往往不会一成不变，而是随着时间的推移不断发生变化。因此，必须在推荐过程中考虑用户的兴趣变化。

由于用户兴趣会随着时间变化，所以用户的评分行为越早，代表用户偏好与用户当前偏好的一致性就越弱，在当前的推荐过程中所占的权重也越小。因此，为不同时刻的评论分配不同的权重，能够准确反映用户兴趣的动态变化，提升推荐质量。目前有以下4 种产生时间权重的方法［22］：模拟遗忘曲线［23］、建立线性时间函数［24］、建立非线性时间函数［25］、时间窗技术［26］。

1.3 矩阵分解

矩阵分解可在一定程度上缓解传统基于近邻模型的数据稀疏性等问题，目前在推荐领域已有广泛应用。其基本思想［8］是将一个高维稀疏的原始用户——项目评分矩阵R∈Rn×m分解为两个低维潜在特征矩阵，即用户潜在特征矩 阵P∈Rn×f和项目潜在特征矩阵Q∈Rf×m，如 式（1）所示：

其中，用户u和项目i的特征向量分别由pu和qi表示，用户u对项目i的评分如式（2）所示：

实际上，矩阵分解是通过最小化预测评分与实际评分的差异以寻找最优pu和qi，目标函数如式（3）所示：

2 融合项目质量和时间的矩阵分解推荐算法

随着时间变化，用户对项目的兴趣会生变化，越早的评分行为对用户当前兴趣的反映程度越弱。同时，用户对项目的评分在一定程度上也会受到项目自身质量的影响，从而导致用户兴趣偏好的计算存在偏差，影响推荐效果。基于此，本文在构建用户——项目类型兴趣度矩阵和采用矩阵分解预测用户评分时，引入项目评分标准差作为衡量项目质量影响用户评分的质量因子，同时引入融合信息保持期的时间权重因子，修正用户评分，提高用户——项目类型兴趣度计算未评分项的评分预测准确度。然后，根据用户当前项目类型偏好优化推荐候选集。最后，基于修正后的用户——项目评分，采用矩阵分解预测用户对候选集中项目的评分，并将top-N 项目推荐给用户。本文算法主要由3部分组成：①构建用户——项目类型兴趣度矩阵；②产生推荐候选集；③预测评分并生成推荐。算法的整体框架如图1所示。

2.1 构建用户——项目类型兴趣度矩阵

准确获悉用户偏好是实现高质量推荐的必要条件，而用户偏好不仅与用户历史评分相关，与项目类型的联系更为密切。例如，用户1 更喜欢动作片、喜剧，用户2 更喜欢音乐剧、文艺片，因此在推荐过程中应针对不同用户的偏好，推荐符合的项目。考虑到项目的标签信息中包含项目的类型信息。因此，用户对项目的点击或评价行为可在一定程度上反映用户对该类项目的偏好态度。此外，用户对项目的实际评分可具体反映用户的偏好程度。基于此，本文根据用户——项目评分和项目类型信息计算用户对项目类型的兴趣度，构建用户——项目类型兴趣度矩阵（UTI），获得用户当前项目类型偏好，如式（4）所示：

其中，Inter(u)t表示用户u对项目类型t的兴趣度，Iu，t表示用户u评价过的且项目类型为t的项目集合，ru，i表示用户u对项目i的实际评分。如式（4）所示，兴趣度Inter(u)t的大小由两个因素决定：①项目类型出现的次数；②用户对该项目类型的偏好程度。如果一个项目类型在用户的历史评价行为中出现频率越高，越能说明用户对该类型感兴趣。同理，用户对一个项目类型的评分越高，说明对该类型的兴趣程度越高。

Fig.1 Algorithm framework图1 算法框架

然而，由于用户对项目类型的兴趣会随着时间推移而发生变化，故用户对项目的历史评分对用户当前兴趣的反映程度在逐渐下降。此外，项目自身质量也会对用户兴趣产生影响。例如，用户1 喜欢动作片，不喜欢文艺片，虽然影片1 为文艺片，但是由于该影片剧情扣人心弦、好评如潮，用户1 为其评分5 分，然而该评分无法证明用户1 对文艺片的兴趣度为5。因此，需要对用户评分进行修正，消除项目质量带来的评分误差。

2.1.1 修正用户——项目评分

步骤1：引入质量因子消除项目质量对用户评分产生的偏差。

文献［16］将项目评分标准差作为衡量项目质量影响用户评分的质量因子，如式（5）所示。

其中，WQ(i)表示项目i的质量因子权重，Ni表示项目i的评分总个数，ri，m表示项目i的第m个评分,表示项目i的平均分。项目i的离散性越大，对用户偏好的反映程度越高，质量权重也就越大。

项目的评分越集中，标准差越小，说明项目质量对用户评分的影响越大，就越难反映用户的兴趣偏好；反之，项目评分越分散，说明项目质量对用户评分的影响越小，对用户兴趣偏好的反映程度越高。

本文采用公式（6）消除项目质量带来的用户评分偏差。

其中，ru，i'表示修正后用户u对项目i的评分，ru，i表示用户u对项目i的原始评分，WQ(i)则是由公式（5）计算出的质量权重。

最后，利用如式（7）所示的最小——最大标准化公式将加权修正后的评分映射到评分区间［1，5］，标准化后记为

其中，表示标准化后的评分，R表示标准化前的评分，Rmax和Rmin分别表示标准化前评分的最大值和最小值。

步骤2：引入时间因子模拟用户兴趣的动态变化。

本文参考文献［27］建立融合信息保持期的时间衰减函数，获得不同时刻的时间权重，如式（8）所示。

其中，λ=表示衰减因子，T0表示信息半衰期，即信息经过T0的时间，影响力减少一半；T'表示信息保持期，即信息在T'时间内影响力保持不变；t=tnow-tu，i，tnow表示用户u最晚评分时间，tu，i表示用户u对项目i的评分时间。

步骤3：通过公式（9）对用户评分进行引入时间权重的加权处理。最后，将加权修正后的评分再次利用公式（7）进行最小——最大标准化，标准化后记为，即为既消除了项目质量的影响，又能够体现用户兴趣变化的用户评分。

2.1.2 构建用户——项目类型兴趣度矩阵

步骤1：根据基于项目质量和时间因素修正的用户评分建立用户——项目评分矩阵R，如式（10）所示。

假设现有一组用户u1、u2、u3、u4对项目i1、i2、i3的评分，引入质量因子和时间因子加权修正后的矩阵R如表1所示。

步骤2：根据项目所具有的类型信息构建项目类型矩阵T，当项目i具备类型t时，对应t项的值记为1，否则为0，如式（11）所示。

Table 1 User-item rating matrix（R）表1 用户——项目评分矩阵（R）

假设根据上述项目i1、i2、i3的类型信息构建的项目类型矩阵T如表2所示。

Table 2 Item type matrix（T）表2 项目类型矩阵（T）

步骤3：根据矩阵R和T构建用户——项目类型兴趣度矩阵UTI，具体步骤如下：

Step1：根据用户——项目评分矩阵R获取用户评价过的项目及评分。例如，u1评价过项目i1，i2和i3，评分分别为3、5、2。

Step2：根据项目类型矩阵T获取每个项目的类型信息。例如，项目i1拥有t1和t3两种类型。

Step3：根据公式（4）计算用户——项目类型兴趣度。例如，u1对t1的兴趣度为Inter1，1=1 × 3=3；u1对t2的兴趣度为Inter1，2=1 × 5+1 × 2=7；u1对t3的兴趣度为Inter1，3=1×3+1×5=8；u1对t4的兴趣度为Inter1，4=1 × 2=2。

Step4：将Step3 计算得到的用户——项目类型兴趣度，利用公式（7）进行标准化，映射到评分区间。以u1为例，对各类型的兴趣度标准化后分别为：

最后，得到的用户——项目类型兴趣度矩阵UTI如表3所示。

Table 3 User-item type interest matrix（UTI）表3 用户——项目类型兴趣度矩阵（UTI）

由表3 可见，用户u1对t2和t3的兴趣度很大，而对t1和t4的兴趣度较小，说明用户u1更加偏好具有t2和t3类型的项目。

2.2 引入项目类型偏好优化候选集

考虑到用户对不同项目类型具有不同的兴趣度，为其推荐感兴趣类型的项目可在一定程度上提高推荐的准确率，满足用户的个性化需求。因此，本文引入用户对项目的类型偏好改进项目候选集的选择。具体步骤如下：

步骤1：设置类型偏好阈值，获取用户当前项目类型偏好。将参数θ作为判断用户对项目类型偏好程度的阈值，当兴趣度≥θ时，说明用户当前对该项目类型感兴趣，反之则说明不感兴趣。以阈值作为划分条件，以便于根据UTI矩阵获取每个用户当前的项目类型偏好。

步骤2：生成符合用户偏好的候选集。根据步骤1 步得到的用户当前项目类型偏好，将具有该类属性的未评分项目组成推荐候选集。

2.3 矩阵分解预测评分

由于用户对项目的原始评分无法体现用户的兴趣变化，同时还受到项目质量的影响而产生评分偏差。因此，本文引入质量和时间因子修正后的用户评分进行矩阵分解，通过寻找用户、项目的潜在特征向量实现对候选集中项目的评分预测，并向用户推荐top-N 项目。

2.4 算法描述

融合时间因素、项目质量和项目类型信息的矩阵分解协同过滤算法的具体流程如算法1所示。

算法1：融合项目质量和时间因素的矩阵分解协同过滤算法。

输入：带有时间戳的用户评分信息（u.data），项目类型信息（u.item），目标用户u，半衰期T0，信息保持期T'，类型偏好阈值θ，矩阵分解潜在特征数k，推荐列表长度N。

输出：针对目标用户u生成的top-N 推荐列表。

步骤1：引入质量和时间因子修正用户评分。根据公式（9）计算基于质量和时间加权后的用户评分，并利用公式（7）标准化到评分区间，得到修正的用户——项目评分

步骤2：构建用户——项目类型兴趣度矩阵UTI。分别根据公式（10）、公式（11）构建用户——项目评分矩阵R和项目类型矩阵T，再根据公式（4）计算用户对项目类型的兴趣度，并标准化到评分区间，构建UTI矩阵。

步骤3：根据步骤2 得到的UTI矩阵，结合类型偏好阈值θ，获取用户u当前的项目类型偏好。

步骤4：根据步骤3 中获得的用户项目类型偏好，将具有该类型属性的未评分项作为推荐候选集。

步骤5：矩阵分解。将步骤2 中构建的矩阵R分解为代表用户潜在偏好特征的矩阵P和代表项目潜在偏好特征的矩阵Q。

步骤6：预测评分。根据公式（2），预测用户u对项目i的评分。

步骤7：产生top-N 推荐列表。对于推荐候选集中的所有项目，重复步骤6，计算用户u对所有候选集中项目的预测评分并排序，并将预测评分最高的top-N 作为推荐列表。

3 实验分析

3.1 实验设置

MovieLens 数据集是经典电影评分数据集，本文使用其中的MovieLens-100K 数据集和MovieLens-1M 数据集分。

由图2、图3 可见，QTW-MFCF 算法的准确率和召回率别进行实验，将其记为M1和M2，对数据集的详细描述如表4所示。

Table 4 Description of data sets表4 数据集描述

数据集一共包含19 种电影类型，本文实验中使用除unknown 类型外的18 种类型，并将用户近期20%的评分数据作为测试集，剩下的80%则作为训练集以挖掘用户偏好。

为了检验QTW-MFCF 算法的性能，本文将其与传统基于物品的协同过滤算法（IBCF）、结合评分比例因子和商品属性的协同过滤算法（RFIA-CF）［12］、基于用户评分偏好模型、融合时间因素和物品属性的协同过滤算法（PTPItem-CF）［14］、融合用户偏好和物品相似度的概率矩阵分解推荐算法（UPIS-PMF）［19］、融合时间的矩阵分解协同过滤算法（MFTWCF）［28］及融合项目质量的矩阵分解协同过滤算法（QW-MFCF）进行分析比较实验。

3.2 实验指标

目前有多个指标可用来评价推荐算法的性能，而对于top-N 推荐则一般采用准确率（precision）、召回率（recall）及F1值度量，计算公式如式（12）-式（14）所示。

其中，U表示所有用户集合，R(u)表示用户u推荐的top-N 项目列表，T(u)表示测试集中用户u的实际评价项目列表。

3.3 结果分析

QTW-MFCF 算法中一共涉及了4 个参数，即矩阵分解的潜在特征个数k，用户对项目类型偏好的阈值θ，信息半衰期T0及信息保持期T'，下面分别设置实验确定4 个参数，并在不同推荐列表长度下与IBCF 算法、RFIA-CF 算法、PTP-Item-CF 算法、UPIS-PMF 算法、MFTWCF 算法和QW-MFCF 算法进行性能比较。

3.3.1 潜在特征个数k对实验结果的影响

Fig.2 Influence of k on results in M1 dataset图2 M1数据集中潜在特征个数k对结果的影响

Fig.3 Influence of k on results in M2 dataset图3 M2数据集中潜在特征个数k对结果的影响

实验设置推荐列表长度N=10，类型偏好阈值θ=3，信息半衰期T0=30，信息保持期T'=3，通过比较不同k值的准确率和召回率确定最优潜在特征个数k。首先，实验以间隔为5 确定最优k值范围；然后，以间隔为1 确定最优k值。图2、图3 分别给出了潜在特征个数k在M1和M2数据集上的结果。随k的逐渐增大呈现先增大后减小的趋势。在M1数据集上，当k值的取值范围为［15，20］时，k=19 时效果最好，准确率和召回率分别比k=10 时提高了6.78%和7.62%；在M2数据集上，当k值的取值范围为［25，30］时，k=28 时效果最好，准确率和召回率分别比k=10 时提高了11.6% 和21.76%。实验结果证实，潜在特征个数k的选取对矩阵分解效果的优劣至关重要，还可看出M1数据集的最优k值相较M2数据集更接近其所包含的电影类型种类，这可能是由于M2数据集内包含的项目数量更多，且每个项目类型属性不唯一，使项目间存在更多的类型组合差别。

3.3.2 类型偏好阈值θ对实验结果的影响

本文设置推荐列表长度N=10，信息半衰期T0=30，信息保持期T'=3，M1和M2数据集的潜在特征数k分别为19和28，比较类型偏好阈值θ分别取1、2、3、4 时的准确率和召回率。

Fig.4 Influence of θ on results in M1 dataset图4 M1数据集中类型偏好阈值θ对结果的影响

由图4、图5 可见，在M1和M2数据集上都是θ=2 时效果最好。M1的准确率和召回率相较于θ=1 时分别提高了0.778%和0.428%，而M2的准确率和召回率则相较于θ=1时分别提高了1.338%和0.763%。该结果说明根据用户的项目类型偏好对候选集进行优化，可进一步提高推荐效果。此外，当阈值θ>2 后，M1和M2数据集的准确率和召回率都存在明显的下降趋势，这主要是因为随着阈值θ的不断增大，推荐列表中项目的多样性不断减小，以致于无法满足用户的个性化需求，造成推荐效果不佳。

Fig.5 Influence of θ on results in M2 dataset图5 M2数据集中类型偏好阈值θ对结果的影响

3.3.3 信息半衰期T0对实验结果的影响

本文设置推荐列表长度N=10，类型偏好阈值θ=3，信息保持期T'=1，M1和M2数据集的潜在特征数k分别为19和28，信息半衰期T0取值范围为10～60，间隔为5。

Fig.6 Influence of T0 on results in M1 dataset图6 M1数据集中信息半衰期T0对结果的影响

Fig.7 Influence of T0 on results in M2 dataset图7 M2数据集中信息半衰期T0对结果的影响

由图6、图7 可见，在M1数据集上T0=40 时，即时间经过40 天，用户评分的影响力衰减为原来的一半时，效果最好；而在M2数据集上，当T0=15 时推荐效果最好，说明M2中的用户兴趣迁移现象相较M1更频繁，而实际上M2所包含的项目数量大约为M1的2.5 倍，用户拥有的选择性更大，因此兴趣迁移更容易发生。

3.3.4 信息保持期T'对实验结果的影响

本文设置推荐列表长度N=10，类型偏好阈值θ=3，信息半衰期T0=30，M1和M2数据集的潜在特征数k分别为19和28，比较不同信息保持期T'下的准确率和召回率。由图8、图9 可见，尽管在M1和M2数据集上，算法的准确率和召回率随T'增大呈现出不同的变化趋势，但都当T'=3 时结果最优，说明用户兴趣在3 天内保持不变，与实际相符合，具有一定合理性。

Fig.8 Influence of T'on results in M1 dataset图8 M1数据集中信息保持期T'对结果的影响

Fig.9 Influence of T'on results in M2 dataset图9 M2数据集中信息保持期T'对结果的影响

（5）算法性能对比

实验通过设置不同推荐列表长度N来比较各算法的准确率和召回率，以此检测算法性能。N的取值范围为［5，30］，间隔为5。

由图10、图11 可见，随着N不断增大，在两个数据集上各算法的准确率均有不同程度的下降，而召回率则相反。其中，本文提出的QTW-MFCF 算法的准确率和召回率在不同推荐长度N都最高。表5 给出了在top-10 推荐下，不同数据集上各算法的准确率、召回率及QTW-MFCF算法相对各对比算法的提升率。

Fig.10 Performance contrast of each algorithm with different recom⁃mend lengths N on M1 dataset图10 M1数据集不同推荐列表长度N下各算法的性能比较

从图10、图11及表5可见，在M1和M2数据集上，QTW-MFCF 算法推荐效果最好。经过实验证明在推荐过程中利用类型偏好优化候选集可获得更好的推荐准确度。

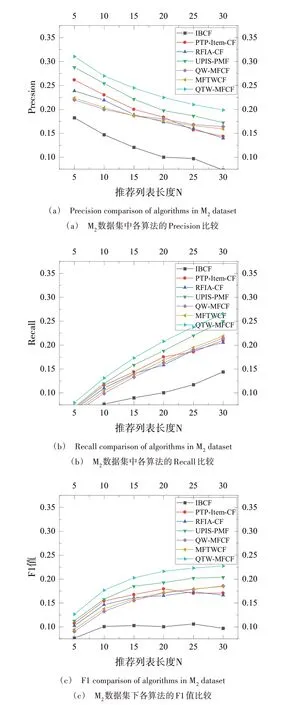
Fig.11 Performance contrast of each algorithm with different recom⁃mend lengths N on M2 dataset图11 M2数据集不同推荐列表长度N下各算法的性能比较

Table 5 Comparison of precision and recall of each algorithm on dif⁃ferent data sets表5 不同数据集上各算法的准确率和召回率比较

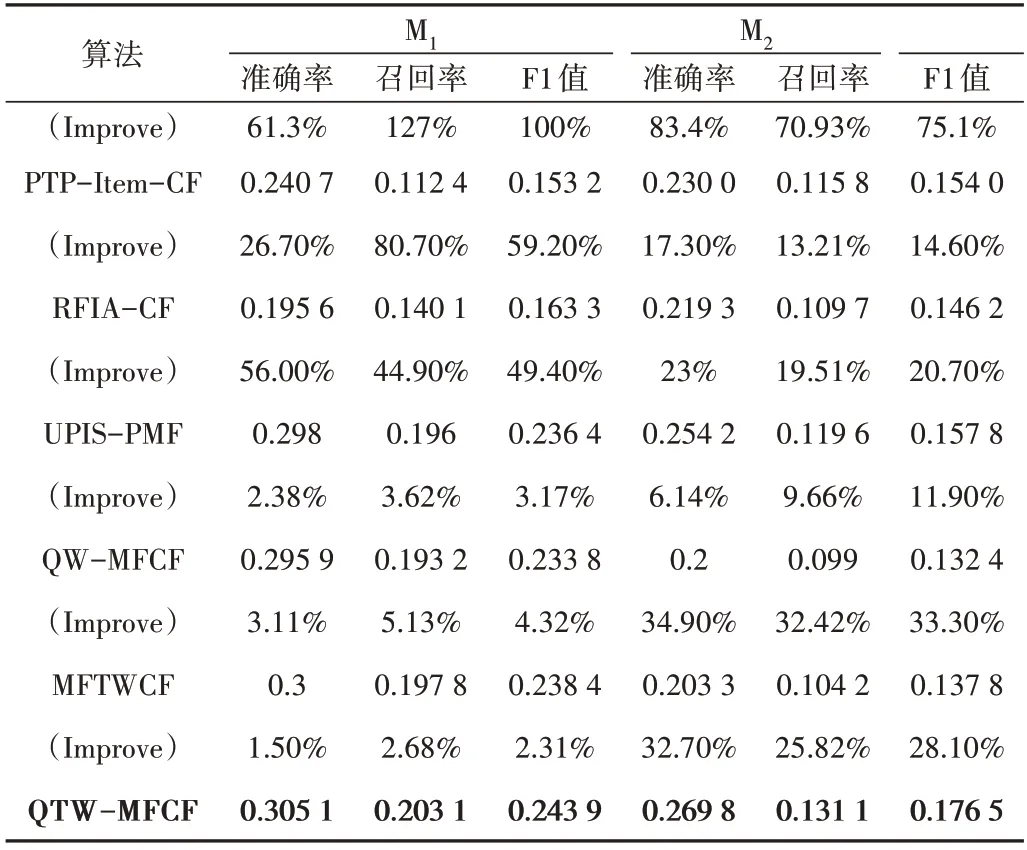
续表

4 结语

本文提出的QTW-MFCF 算法，通过消除项目质量影响和融合时间因素构建用户——项目类型偏好，基于此对推荐候选集进行优化。实验证明，该算法推荐的准确率和召回率均有所提高，证明了在挖掘用户偏好时应考虑用户兴趣变化和项目质量对用户行为的影响，但该算法在提高推荐准确率的同时，会损失部分推荐多样性。因此，下一步将考虑在保持现有推荐准确率的同时提高推荐多样性。例如，在考虑项目类型偏好的同时，增加人与人之间的信任关系［29］对用户行为的影响，并以此扩展推荐候选集，提高推荐质量。