以兴趣为导向的高等数学课堂教学改革与实践

魏 杰, 董 珺

(兰州工业学院 基础学科部, 甘肃 兰州 730050)

高等数学课程作为理工类及经管类学生一门重要的基础课程，是学生学习后续课程和解决科技问题的重要工具。例如，高等数学不仅是经济学中的一种重要的表述工具，同时也成为经济学中的一个重要的分析工具；土木工程专业的学生需要利用高数当中的导数以及偏导数当中的知识；通信工程专业的学生需要对重积分以及无穷级数知识进行应用；材料学科中，在溶体中存在异质相粒子，会在热作用下自发生长，这种长大过程就需要用到高等数学中微分方程来解决，等等。而要会用数学知识解决专业问题，首先要理解数学理论，打好数学基础，然后才能与实际相结合，而不能拔苗助长，数学没学好就想如何去应用。文中的相关概念和例子见文献[1-2]。

1 学生在学习高等数学中存在的问题

由于一般本科院校学生的数学基础较弱，对数学的认知不够明确，导致对数学的学习热情不高，主要存在以下问题：① 高等数学中的概念过于理论化；② 高等数学中的性质、法则过于抽象；③ 高等数学中定理的适用范围不够清晰；④ 高等数学中的某些题型的解题方法过于繁琐。

2 良好的教学方法是启发学生学习兴趣的源泉

2.1 通过通俗的语言及简单易懂的例子解释理论概念

高等数学中的许多概念过于抽象，且晦涩难懂。这也是部分学生认为其是“高高的挂在树上”，从一开始就不愿意主动学习的原因。例如，极限是高等数学的重要工具，极限概念是学习高等数学的理论基础，但由于太过抽象，学生很难理解，从而影响了后续的学习热情。在讲数列极限定义时，首先作如下解析：

②ε是用来衡量xn与a的接近程度，既有任意性,又有确定性。

③N不唯一,极限的定义并不要求取到最小的或最佳的正整数,我们只关心N的存在性。

④ 一个数列收敛与否,收敛于哪个数,与这一数列的前面有限项无关.换句话说,你可以随意修改数列的有限项,而不至于影响其收敛性。

然后给出下面例子，帮助学生理解。

例1 数列{xn}收敛于实数a等价于( )

(A)∀ε>0,在(a-ε,a+ε)内有数列{xn}的所有项

(B)∀ε>0,在(a-ε,a+ε)内有数列{xn}的有限项

(C)∀ε>0,在(a-ε,a+ε)外有数列{xn}的无穷项

(D)∀ε>0,在(a-ε,a+ε)外有数列{xn}的有限项

2.2 通过拓展及总结运算法则，达到正确使用的目的

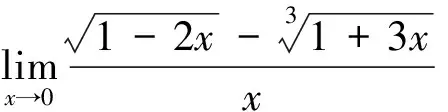
对于上面的∞-∞，很多同学马上写成0，也有同学写成不存在。

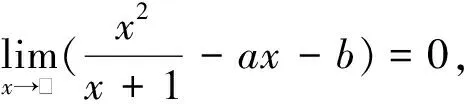
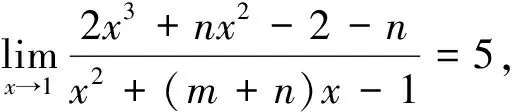
针对诸如上述问题，在讲解极限的四则运算法则时，笔者一般进行如下拓展与总结：

① 只有当f(x)与g(x)的极限都存在时,才能使用四则运算法则.否则,很容易产生谬误。

② 以下两个结论,经常出现在已知极限求参数类型的题目中。

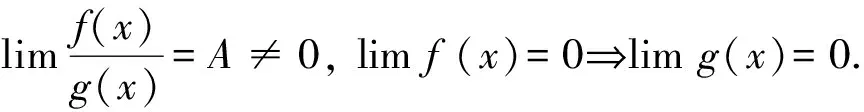
③ 一般,当a0≠0,b0≠0,m,n为非负整数时有

这种方法称为“保留最大项法”或“抓大项法”。

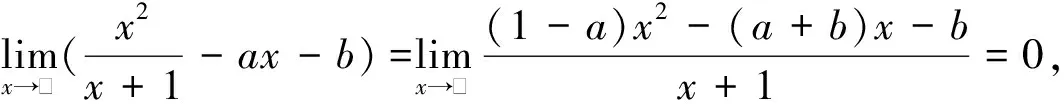
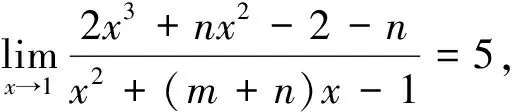
最终解出m=-2,n=2.

2.3 通过错例分析使用条件，避免错误使用定理

高等数学中的定理是计算和证明问题的理论依据，尤其是一元函数部分，但如果按照一般教科书上所写，学生很难正确使用。笔者在讲授时，通常会通过错例及反例分析，避免错误使用定理，如学生学习了牛顿-莱布尼茨定理之后，会错误地认为存在原函数和存在定积分是一致的；又如，等价无穷小替换定理是计算极限的重要方法，但很多学生在使用时经常出现错误。

为此，对等价无穷小替换定理作如下解释：等价无穷小替换对分子或分母中的因式可以进行代换，若极限中分子或分母中的无穷小是以和或差的形式出现,则尽量不要代换,否则将可能导致错误的结果。

2.4 简化计算方法，提高解题效率，增强学习兴趣

“兴趣是最好的老师。”许多学生不喜欢学高等数学的原因在于很多题目的解决方法过于麻烦，计算量过大，往往需要花费很长时间才能解决一道题目(有时候还空欢喜一场)，缺乏获得感和成就感。笔者在授课时，会经常提出新的方法和解题技巧，将很繁琐的解题过程进行简化，有时候甚至会一步成型，让学生与教科书上的解法对比，可能教科书上需要十几步才能解决的问题，我们需要三五步就能快速解决,以此来提高学生的学习兴趣。

例如，对于“1∞”型的极限，教科书上告诉我们需要凑成第二类重要极限的形式：

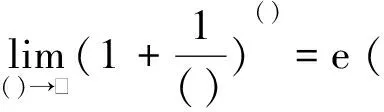
再使用结论。

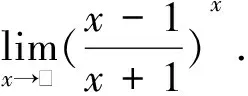
上面两种方法是这种基本问题的一般解决方案，不仅过程麻烦，会导致部分学生难以解决，经常出错，降低了获得感和成就感，而且对复杂如

这类问题，基本无法下手。这样让喜欢做课外拓展的学生感觉教师上课所讲方法是否合理高效，甚至怀疑老师的授课水平，久而久之对课堂失去兴趣，更谈不上主动学习了。

笔者在处理这一问题时，会首先证明一个结论：

设limu(x)=1, limv(x)=∞,则有limu(x)v(x)=elimv(x)[u(x)-1].

又如，二重积分的计算是很多学生提起来就头痛的事情，如何选坐标系，系选好后如何定限，限定好后又如何计算等问题一步接一步。笔者在讲解时结合对称性和形心公式，对部分复杂问题进行简化，做到真正的化繁为简，更有获得感和成就感。

解析首先画出积分区域D如图1所示,是正方形减去半圆,记正方形所围区域为D1,半圆所围区域为D2,则

图1 积分区域D

2.5 通过一题多解提升解决问题的能力

解题时多个方法多条路，多储“备胎”，应由“一题一法”向“一题多法”转变，才能不会“书到用时方恨少”。这样学生在练习时才能“条条道路通罗马，此中必有我一条”。

3 结语

从概念的深度理解、法则拓展及解题方法总结等方面，提升学生学习高等数学的获得感和成就感，以此增强学生的学习兴趣和主观能动性，使得学生学会学习，爱上学习。