多跨无支座整体式刚构桥地震反应分析
师新虎 蓝先林 范安军
(1.四川公路工程咨询监理有限公司 成都 610041;2.贵州省交通规划勘察设计研究院股份有限公司 贵阳 550081)
随着我国“四纵四横”高铁网络的形成,越来越多的桥型在实际中得到了应用,其中多跨简支梁、连续梁桥、连续刚构桥[1-3]仍作为主要跨线桥梁占主导作用。无支座连续刚构桥[4-6]作为一种新桥型,全桥不设支座,边墩与中墩均与主梁固结形成刚架结构,其最大特点在于取消了支座,抗震性能好,结构轻盈美观,节约圬工量,彻底避免了常规桥梁运营后期大量支座检测及维养工作,节约支座安装与桥梁养护费用,桥梁整体维养周期延长,同时,避免了因为更换支座导致桥梁区域性停运而带来的社会影响。该新型体系桥梁目前在国内高速铁路桥梁上应用极为罕见。
我国作为地震频发国家[7],随着高速铁路网的不断发展,高速铁路不可避免地穿越地震高烈度区[8-11],如何对无支座连续刚构桥的地震受力特性、变形特征、墩柱的纵、横向刚度限值及主梁的竖向刚度取值进行合理分析与设计是该新型体系桥梁研究过程中的必要环节。
基于上述研究,本文以多跨无支座整体式刚构桥为研究背景,基于OpenSees软件平台建立三维非线性有限元模型进行非线性时程分析,探究其在多遇地震、设计地震、罕遇地震下墩柱的受力特点与变形特征,同时对单薄臂的合理臂厚取值进行参数分析,最后对墩柱的塑性铰区域进行研究。
1 工程背景
3跨(3×72 m)无支座预应力混凝土整体式刚构桥,一联全长216 m,主梁和桥墩均采用C50混凝土,全桥不设支座(边墩及中墩均与主梁固结形成刚架结构),刚构主梁采用变截面单箱单室混凝土箱梁,桥墩处梁高6.6 m,跨中梁高4.1 m,梁高按圆曲线变化。边墩采用单薄臂矩形截面,中墩采用双薄臂矩形截面。限于篇幅文中仅给出所研究关键截面的具体构造与尺寸,详见图1、图2。桥位地震烈度为VII度,II类场地,地震动峰值加速度为0.2g。

图1 单薄臂边墩关键截面(单位:cm)

图2 双薄臂矩形中墩关键截面(单位:cm)
2 抗震设防目标
根据桥梁实际所处的工程场地特性及地震安评报告,另外参考GB 50111-2006 《铁路工程抗震设计规范》、CJJ 166-2011 《城市桥梁抗震设计规范》相关条款及类似桥梁的研究成果,桥梁相应的性能目标确定和具体抗震设防标准参见表1。

表1 桥梁抗震性能目标
3 地震动合成
将地震危险性分析得出的具有概率含义的基岩地震动峰值和反应谱作为目标谱,采用三角级数迭加法合成基岩地震动,作为场地地震动力反应分析的输入地震动时程,该时程含有概率含义,并与特定地震环境相关。
反应谱与功率谱之间存在如下近似转换关系。
(1)
式中:ε为阻尼比;S(ω)为功率谱;Sa(ω)为目标反应谱;T为持续时间;r为超过目标反应谱值的概率。通过三角级数迭加法,生成零均值的平稳高斯过程。
(2)
(3)
式中:φk为[0,2π]区间内均匀分布的随机相位角;Ck与ωk分别为第k个频率分量的幅值和频率;f(t)为强度包线函数;α(t)为一平稳的高斯过程。
将平稳时程乘以非平稳强度包线,得到非平稳的加速度时程,非平稳包线函数为如下形式。
(4)
式中:(0,t1)为振幅增大段;(t1,t2)为振幅平稳段,(t2,T)为振幅减少段;c为峰值衰减系数。
对幅值谱进行多次迭代修正,即可使反应谱向目标谱逼近。采用上述理论方法共拟合出3条人工地震动时程,地震持时为40 s,时间步长为0.02 s,合成的人工地震动须采用频域方法进行迭代修正以提高精度。
人工地震动时程反应谱Sa(ω,ζ)可按式(5)计算。

(5)
式中:Sa(ω,ζ)为人工地震波反应谱;ω和τ分别为结构的固有频率与阻尼比;h(·)为单位脉冲响应函数。对合成的人工地震波进行幅值修正,并将调整后的地震动转化为反应谱,再与目标谱作比值进行精度值检验,直到精度满足要求。
(6)
按下式进行幅值调整:
(7)

人工合成地震动的反应谱与规范谱对比见图3。

图3 拟合反应谱和规范谱对比
4 有限元模型及动力特性
为综合体现相邻联梁体、桥跨之间的相互影响规律,并增强模拟结果的可靠性,本文基于OpenSEES软件平台建立相邻两联(总计6跨)桥梁非线性分析模型,模型示意本构关系见图4。
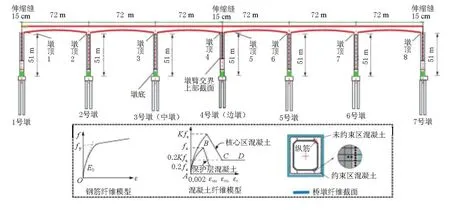
图4 三维有限元模型
其中主梁采用基于位移的梁柱单元(displacement-based beam-column element,DBE)进行模拟,并通过对节点两端赋予不同截面属性的方式实现主梁的变截面;采用柔度法的非线性梁柱单元结合纤维截面来模拟强震作用下桥墩的弹塑性变形,该单元以单元内力差值函数为基础,单元的平衡条件和变形协调条件在单元状态确定阶段中总是严格满足的。纤维模型中单元的非线性主要体现在纤维材料的非线性应力-应变关系,核心区和保护层混凝土材料采用Concrete02来定义,其非线性是基于Kent-Scott-Park本构模型;钢筋采用Steel02进行定义,其本构模型采用Giuffré-Menegotto-Pinto模型。桩土相互作用通过采用“6弹簧法”在承台底部施加6自由度等效刚度来实现,其基础的等效弹簧刚度取值见表2、表3。

表2 边墩基础弹簧刚度矩阵

表3 中墩基础弹簧刚度矩阵
5 地震反应分析
本文暂不考虑动水作用、行波效应,以及多点激励的影响,基于理论方法合成的3条非平稳地震动分别对桥梁进行多遇地震、设计地震和罕遇地震下的地震响应分析,每种工况取3条地震激励下的最大响应作为最终结果。多遇地震、设计地震和罕遇地震的地震动峰值加速度分别取0.08g、0.215g和0.38g。
5.1 多遇地震响应分析(50年超越概率63%)
多遇地震作用下,各桥墩墩顶纵向位移响应分析图见图5。由图5可知,4号墩顶位移达到峰值约为13.8 cm,而梁端碰撞间隙仅为15 cm,由此说明该结构体系较柔,尤其对于单肢薄壁边墩其墩顶位移相对较大,相邻2联共墩处梁端可能会引发碰撞的风险。

图5 多遇地震下墩顶纵向位移响应

表4 桥墩各控制截面抗震验算结果 N·m
5.2 设计地震响应分析(50年超越概率10%)
设计地震作用下各桥墩墩顶纵向位移响应及典型截面的塑性耗能滞回曲线分析图见图6。

图6 设计地震下墩顶纵向位移响应
从图6可知,设计地震作用下,边墩单肢的墩顶位移达到峰值约为26.8 cm,而梁端碰撞间隙仅为15 cm,相邻两联共墩处梁端可能会发生大概率的碰撞效应,因此在设计地震作用下通过在共墩处梁端设置限位器或减隔震装置来阻止或缓解梁端碰撞局部损伤是非常有必要的。表5给出了桥墩各控制截面抗震验算结果。
由表5可知,设计地震作用下,边墩墩顶截面已接近进入塑性的临界状态,且边墩较中墩截面钢筋更早屈服,说明边墩比中墩更控制设计。
设计地震荷载工况下单肢薄臂边墩弯矩内力随不同臂厚取值的参数分析结果,见图7。
由图7可知,设计地震作用下,墩底弯矩随着臂厚增大而增大,尤其对于边墩(4号墩)及与之相邻的3号墩、5号墩的影响更为明显,其中当臂厚取1.5 m时,墩底弯矩内力均处于最小状态;而臂厚增大导致的墩顶弯矩内力随峰值地面加速度的变化规律与墩底弯矩变化规律略有不同,臂厚改变对4号墩、5墩的墩顶弯矩影响更为显著,其中臂厚增至1.8 m时,墩顶弯矩略有降低。
因此,针对铁路高墩无支座整体式刚构桥,设计地震下,不同的臂厚取值会对桥梁墩顶与墩底内力响应产生极大的影响,当臂厚取1.6 m时,边墩墩顶的损伤程度最大,当臂厚大于1.6 m时,增加臂厚会增大墩底的弯矩响应,但有助于减小中墩墩顶的弯矩内力,进而会减小中墩墩顶的损伤程度。综合考虑,边墩设计截面臂厚取值1.5 m较为合理。
5.3 罕遇地震响应分析(50年超越概率2%)
边墩墩顶的滞回曲线图见图8,滞回曲线呈梭形,形态较饱满,说明桥墩在罕遇地震下拥有较大的延性变形能力来耗能,结构延性设计合理。罕遇地震作用下各桥墩墩顶纵向位移响应图见图9a),由图9a)可知,罕遇地震作用下各桥墩墩顶纵向位移均超出了49 cm,墩顶位置均发生了较大的塑性变形,对于边墩而言可能会发生更大的延性变形来适应强震需求。

图8 边墩墩顶滞回曲线
罕遇地震作用下墩顶与墩底的弯矩、剪力变化规律图分别见图9b)与9c)。
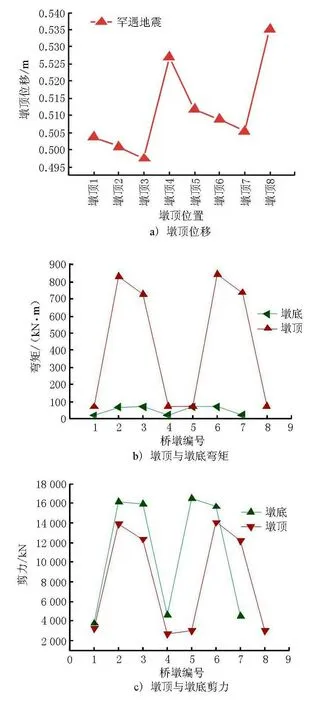
图9 墩顶、墩底地震需求
由图9可见,墩顶的弯矩内力明显要大于墩底的弯矩内力,墩顶与墩底的弯矩内力最大相差约10倍,其中中墩的墩顶截面较墩底截面更容易进入损伤状态。2号墩与6号墩墩底的弯矩内力最大,边墩墩底的弯矩内力最小;2号墩与5号墩墩底的剪力最大,两侧边墩墩底剪力最小,4号墩墩顶剪力处于最小状态。
罕遇地震作用下3号墩(中墩)与4号墩(边墩)沿墩高变化的弯矩包络图与剪力包络图见图10。图中墩高0 m指墩顶截面处,墩高50 m指墩底截面处。
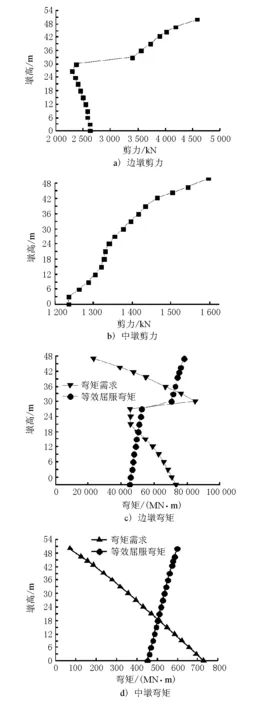
图10 墩身内力包络图
由图10可见,边墩(4号墩)的剪力出现了先减后增的情况,这是因为相邻两联的单肢薄臂墩在墩高35 m处共用一个桥墩,截面臂厚突然增大,截面的剪力也相应变大。而中墩截面,随着墩高变高其剪力则表现出较强的非线性增大,中墩在墩底截面其剪力达到峰值最大。
针对弯矩地震需求,边墩则在墩顶至墩底21 m范围、墩臂交界处5 m范围内截面易进入塑性状态进行延性耗能减震;而中墩则在墩顶至墩底18 m范围内截面易进入塑性状态形成塑性铰,其余中墩截面并未进入延性。罕遇地震作用下中墩墩顶截面、边墩的墩顶与墩臂交界处截面更容易进入塑性状态,形成塑性铰机制,因此,对于该体系桥梁而言,在主梁抗弯刚度相对提高的同时也应注意边墩墩顶截面、墩臂交界处截面抗弯刚度的合理取值,尽量使各桥墩刚度充分发挥达到多途径、协同均衡受力状态以降低桥墩易损位置的损伤,在高烈度地震区域可考虑采取必要的减震装置来减轻边墩墩顶处的纵向变形。
6 结论
1) 高墩大跨无支座整体式刚构桥作为高速铁路上运用的新桥型,其全桥不设支座,彻底避免了常规桥梁运营后期大量支座检测及维养工作,其次结构轻盈美观,上、下部结构均衡协调,主梁抗弯刚度整体提升,跨越能力较强,结构耐久性得到了整体提升,对于跨河、深V形峡谷的桥梁而言,拥有较强的适应性。
2) 设计地震作用下,边墩墩顶截面成为桥墩的最易损截面,其已接近进入塑性的临界状态,且边墩较中墩截面钢筋更早屈服,说明边墩较中墩更控制设计。罕遇地震作用下边墩的墩顶20 m范围、墩臂交界处5 m范围及中墩墩底18 m范围易形成塑性铰区域,因此类似桥梁在设计过程中应加强该区域桥墩截面的抗弯能力设计。
3) 边墩墩顶对其臂厚改变所致的弯矩变化更为敏感,适当增加臂厚会增大墩底的地震反应,但有助于降低墩顶的弯矩需求,进而降低墩顶的损伤程度。因此针对薄臂单肢边墩,其臂厚的合理择取对其地震需求影响至关重要。研究成果可为该类型桥梁的损伤位置风险识别、边、中墩合理刚度取值及墩梁减震措施的优先级决策提供参考依据。

