基于应变式压力传感器的称重定量装置零点校准方法

张国鸣，李生茂，赛喜雅拉图

（国家能源集团神华北电胜利能源有限公司储运中心，锡林浩特 026000）

0 引言

在电子技术、计算机技术等多个学科的相互推动下，高端制造业中的称量研究，也从初始的静态、间断型称重模式，逐渐升级为动态、连续型的称重方式。随着我国制造业转型的深入落实，散状物料贸易计量、包装运输等项目的发展，称重定量装置横空出世，在相关制作业领域行业得到广泛应用[1]。对于此类装置而言，其称重准确度，对于一些高精密的制造零件至关重要。近年来，我国相关行业决议通过的定量高精密零件计量监督管理办法中，制定的误差标准愈加严格。因此，对校准技术的精准度提出了较大挑战，研究出具有实践价值与可行意义的零点校准方法势在必行。

压力传感器作为传感器技术的新兴产物，是应用最普及最成熟的类型之一[2]。为此，基于上述背景分析，本文面向以应变式压力传感器为主要设备，提出一种称重定量装置零点校准方法，其构建的辅助校准设备有助于提升计量精准性，能在一定程度上促进制造业中的计量装置与控制系统的发展，有利于加强我国制造业中，称重定量装置的市场竞争力。

1 应变式压力传感器采集称重定量装置应力

常用的应变式压力传感器一般包含平膜片、膜片顶杆等强度较低的弹性敏感元件，对测量、安装应力不具备良好的敏感性。为提升称重定量装置的零点校准精度，将传感器外壳视作压力敏感元件，根据压力、半径等参数解得应力，为更好地校准装置提供参考依据。

在零点校准称重定量装置的过程中，应变式压力传感器可被用来采集称重定量装置多种弹性变形应力。为此，本章节针对称重定量装置内外压作用下弹性变形应力、外压作用下的塑性区域应力和弹性区域应力、余应力展开传感器采集方法分析。

1.1 称重定量装置内、外压作用下的弹性变形应力

传感器采集相关应力参数：在称重定量装置内压pi与外压pe共同作用下产生弹性变形时，假设称重定量装置外壳内、外半径分别是ri、re，待求解的应力点径向坐标是r，采用下列拉美公式组，求解出径向应力σr、切向应力σθ、轴向应力σz：

下列等式即为应力对应的米塞斯屈服条件：

已知称重定量装置外壳内壁，发生屈服初始阶段的外压pEL，则结合米塞斯屈服条件式，即可推演出该弹性极限压力的传感器计算公式，如式(3)所示：

1.2 称重定量装置外压作用下的塑性区域应力

若传感器采集的弹性极限压力pEL不小于外压pe，称重定量装置外壳处于弹性变形状态。外压pe越大，塑性区域由内而外的变形程度越大。若变形呈轴对称形式，则塑性区形式相同。假定弹性区域与塑性区域的分界面半径是ρ，弹塑性界面中两区域具有相同的径向应力，则下列不等式方程组即两区域的判定条件：

若称重定量装置外壳材质的弹塑性较为理想，且塑性变形满足轴向应力公式，则无需考虑误差，基于米塞斯屈服条件式(2)，使外壳呈轴对称发生变形时的应力，符合下列平衡微分表达式：

式(5)中，d表示无穷小的增量，r表示积分处理应力点径向坐标。然后结合边界条件解得传感器采集的径向应力σr，过程如下所示：

将其与米塞斯屈服条件式合并后，得出下列称重定量装置塑性区域应力的计算公式：

此时，ri≤≤r≤≤ρ。弹塑性分界面的法向压力pρ由下式解得：

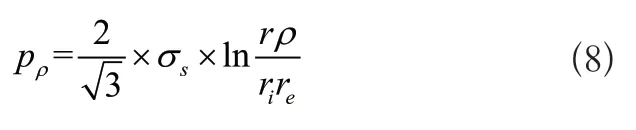
1.3 称重定量装置外压作用下的弹性区域应力

令外壳内半径ri与两区域分界面半径ρ相等，传感器采集的称重定量装置外壳内压pi与分界面法向压力pρ相等，结合拉美式组(1)，通过下列方程组解得传感器采集的称重定量装置弹性区域的径向应力、切向应力及轴向应力：

因分界面上的弹性变形区域正好满足屈服条件，则外壳弹性区域的外压pA与外压pe相等。

1.4 称重定量装置两区域的余应力

令称重定量装置外压pA逐渐趋近于零，根据内部应力的弹性规律演变方式，利用下列方程组所示的径向应力、切向应力及轴向应力增量，描述传感器采集卸载后的应力变化：

加载结束时应力与三种应力增量的和，即卸载后内部的余应力，假设各余应力各是σ`r、σ`0、σ`z，则塑性区域与弹性区域的余应力计算公式分别为：

为避免卸载后传感器出现反向屈服[3]，必须满足外压pA不超过弹性极限压力pEL二倍的不等式条件。

2 应变式压力传感器下的称重定量装置零点校准

采用改进的应变式压力传感器，构建出图1所示的称重定量装置零点校准设备。

图1 称重定量装置零点校准设备架构图

在称重定量装置零点校准设备架构中，主要组成部分为精密重力发生模块、高度调整模块、机架及软硬件部分。其中，硬件部分包含微处理器、显示器、电源、串口和A/D转换器等；软件部分则包含上位机控制、压力显示程序等。

除应变式压力传感器元件的检测元件外，该设备的控制元件也对其达成预期设计目标有直接影响。故通过对比三种常用的直线步进电机（如表1所示），基于校准设备的精密需求，选用电动型直线步进电机作为该校准设备的控制元件较为合理。

表1 常用直线步进电机选型方案

称重定量装置计量准度的影响因素众多，且各因素间相互作用、相互制约，只有深入分析几种计量误差来源，方能优化校准设备的精准度与准确度。各类误差具体分析如下：

1）应力误差

若称重传感器的作用力是P，称重装置自重是P0，结合称重权函数w(x)与重力加速度g，得出下列物料重力作用力的计算公式：

式(12)中，x表示积分公式的函数；q(x)指代质量分布函数。

因实际的定量称重过程中存在一定应力T（上一章节计算可求出），故当物料以倾角α进行输送时，改写物料重力作用力求解式为：

式(13)中，n、l表示托辊个数、长度；表示平均载荷；E表示称重装置的弹性模量[4]；I表示称重装置的面积惯性矩；T0、D0表示应力与非准直度初始值；ΔT、ΔD表示增量。由此推导出称重误差δcz的近似表达式，如下所示：

2）信号测速误差

称重装置在检测、采集、处理定量物料的模拟信号时，会产生非线性、滞后、重复性误差。假定某采样周期内的测速误差为Δv，该误差即物料重量变化率γ1与测速分辨率γ2的乘积，数学表达形式为：

式(15)中，变化率γ1是物料重量增量模拟信号与总重量模拟信号的比值。

对于因A/D转换器位数而产生的误差，可通过浮点运算结构最大程度消除。

3）环境误差

电磁、温湿度、风、粉尘等外界因素均会影响称重装置与校准设备的正常工作。综合考虑各种因素，用下式描述环境因素总误差：

式(16)中，udc、N表示电磁干扰因素及电动势；M表示振动发生次数；W表示温度测量次数；Q表示测量次数；uFL、vFL、K指代风力、风速与测量次数；uwl、J指代粉尘等附着物的重量与密度。

根据计量误差因素在压力传感器上表现出的输入输出非线性变化特征曲线，设计一种误差补偿算法，提升设备对称重定量装置零点校准的精准度与准确度。该算法分为分段线性化处理与抛物线拟合两步骤。首先，划分该特征曲线为j个区间，利用线性插值法[5]解得输入值(ψt，ψt+1)范围的输出值：

式(17)中，λ指代第t区间的直线斜率。

当特征曲线斜率存在较大变化幅度时，利用二次曲线插值法生成抛物线，取代特征曲线。假设抛物线上三个点坐标分别为(ψ1，y1)、(ψ2，y2)、(ψ3，y3)，点对所成直线的斜率各是λ1、λ2、λ3，则抛物线方程式为：

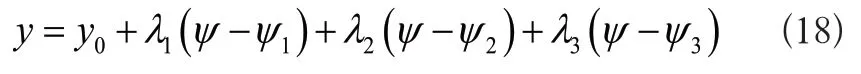
3 仿真试验研究

为验证上述设计的基于应变式压力传感器的称重定量装置零点校准方法的实际应用性能，设计如下测试过程。

3.1 试验准备阶段

不论是校准设备还是称重装置，均对环境条件有较高要求，故在拥有静态标准条件的超净恒温实验室中展开仿真试验。将多个应变式压力传感器均匀安装在某称重定量装置上，该称重装置的六分量平均载荷与输出应变如表2所示。

表2 称重定量装置六分量载荷与输出应变

试验场景如图2所示。

图2 试验现场图

试验中使用的是全自动多头组合称定量秤，其使用参数如下：称重范围：25～125（kg/bag）；定量误差：±0.1%；定量速度：150～300（bag/hr）；电源：220V/380V，50Hz（可调）；功率：3.0kW；温度：-20℃～40℃。

3.2 称重定量装置零点校准结果分析

为有效验证校准方法的可行性，分别从称重定量装置的线性度、灵敏度准确度等多方面开展试验。

在经过本文方法校准后的称重装置六分量正方向上，用砝码进行加卸载，先从空载状态加载至各分量的满量程后，再卸载至空载状态，所得不同分量的输出结果如图3所示。

图3 称重装置六分量加卸载输出示意图

然后将各分量的加卸载输出结果代入线性度、灵敏度等评估指标的计算公式中，取得指标值。以下指标中，拟合优度R2越趋近于1，线性度越优秀；迟滞度CZ与正反差度ZFC均通过式(20)解得，不同的是迟滞度求解前提为同一载荷量，而正反差度计算条件是正向拉伸受力与反向压缩受力的载荷相同，两指标越小，校准效果越好；称重装置的灵敏度随着指标LMD值的增加而上升。

上列各式内，SST、SSR各表示总平方和、回归平方和；εmax表示输出结果最大差值；maxY指代满量程时输出结果；U指代传感器的激励电压。

不同指标的测试结果如表3所示。

表3 称重定量装置六分量载荷与输出应变

表3结果说明，载荷与传感器输出结果之间的线性关系较为理想，加载环节与卸载环节的波动趋势较为拟合，不同方向的加载整合数据也具有较好的线性度。

产生上述结果的原因在于本文方法改进了应变式压力传感器，选用电动型直线步进电机作为校准设备的控制元件，通过深入分析计量误差来源，根据其在压力传感器上表现出的输入输出非线性变化特征曲线，设计出误差补偿算法，有效提升了零点校准的精准度与准确度，故线性度、灵敏度、迟滞度及正反差度均有良好表现，指标值始终位于理想水平。

由于称重定量装置的各分量相互间存在一定干扰，故针对该方向展开此干扰因素对本文方法的零点校准影响。图4所示为加载不同分量时，其余分量在干扰下的最大输出结果。

图4 称重定量装置加载不同分量的输出示意图

分析图4可知，在称重定量装置加载不同分量后，其输出的最大波长基本都集中在1350nm左右，证明其输出较为稳定，也从侧面证明了应用本文方法可以抵御称重定量装置各分量间的干扰，从而提高校准效果。

综上所述，该方法将传感器外壳视作压力敏感元件，减少了影响因素数量，更好地提升了称重定量装置的零点校准精度，根据变形量解得外壳应力，为更精准地校准装置提供了参考依据，故具有较好的干扰抑制效果，能满足称重定量装置的零点校准需求。

4 结语

精密测量技术在医学、制造、军事等重要领域中占据着至关重要的地位，精度要求的数量级也逐渐从微米等级发展为亚纳米等级。当前，我国正以稳健的步伐从农业大国转型为工业大国，生产、加工阶段的物料定量是决定产品质量的关键因素之一，为此，称重定量装置得以广泛应用。随着普及范围与日俱增，该装置精准度受到了越来越多的关注，对相关校准技术也提出了更高的要求。为确保装置的称重精度，本研究提出基于应变式压力传感器的零点校准方法，所取得的研究成果不仅为进一步拓宽称重定量装置的市场应用前景提供了强而有效的助力，而且有望在创新技术的发掘与优化下，发挥出更可靠、更优秀的性能作用。