基于深度学习的混合推荐方法研究①
董露露, 马 宁
(安徽开放大学,安徽 合肥 230022)
0 引 言
互联网技术的迅速发展为用户上网查阅各类信息提供了便利,同时也带来不少问题,如 “信息过载”、“信息爆炸”等。若用户自行在 “信息堆”中筛选出所需的信息,无疑是大海捞针,需要耗费大量的时间和精力,不利于信息的快速查阅使用,至此,推荐系统应运而生[1-2]。推荐系统虽然能够解决信息过载问题,但同时也面临 “冷启动”、“稀疏性”问题,导致推荐效果不佳。近30年来,深度学习不但在图像处理、语音识别等领域上有了新的突破,在推荐系统中也取得了一定成效。如王俊淑等人(2018)在深度学习的基础上,对推荐算法及其趋势进行了探讨,并构建一种更能满足用户偏好的模型[3],以此提高推荐系统性能。冯楚滢等人(2019)针对推荐系统存在的数据稀疏问题,提出了协同深度学习推荐算法,并通过实验对比证明了协同深度学习推荐算法不仅能够有效缓解数据稀疏问题,还可以提高推荐系统的推荐精度[4]。基于上述分析,本文将在深度学习的基础上,探寻出更为适用推荐系统的推荐方法,从整体上提高推荐效果。
1 相关原理概述
1.1 协同过滤推荐方法中的概率矩阵分解原理
虽然通过矩阵分解的方式可以解决新用户存在评分记录缺失的问题,但是面对评价较少的用户其效用则不容乐观。因此,借助贝叶斯法则,在矩阵分解的基础上提出了概率矩阵分解方法,该方法在面对数据集失衡和稀疏问题时,依然能够给出行之有效的推荐。其原理是基于数据分布相关内容对模型参数θ进行修改,相应的叶贝斯公式如式(1)所示。
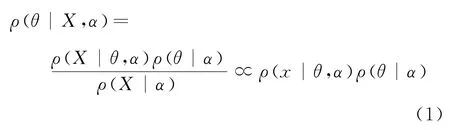
式(1)中,实验用数据集由X 表示,超参数由α表示。
1.2 降噪自编码器原理
在深度学习方法中,自编码器虽然能够对输入数据进行复制,但是其特征却无法得到有效保障[5]。若仅在输入与输出间的误差做文章,以完成对模型的训练工作,那么会出现自编码器的过拟合问题。为了避免这一问题的发生,可在输入层中添加噪声,即通过 “损坏”一部分输入数据方式,生成降噪自编码器。降噪自编码器与自编码器相同,均由一个输入层、一个隐层以及一个输出层组成,二者唯一的区别在于数据使用层面。对自编码而言,其使用的是原始数据,而对于降噪自编码器而言,使用的是 “损坏”数据。输入数据被 “损坏”后,进行编码解码,获取完好的原始数据,如此可增强编码器的鲁棒性。
1.3 降噪自编码器训练过程
与自编码器相比,降噪自编码器训练过程中还引入了一个 “损坏”过程( ) ,其含义为数据样本x生成 “损坏”样本x~ 的概率,结束该环节处理后,便能进行编码解码工作,以获取输出结果。其训练过程如图1所示。
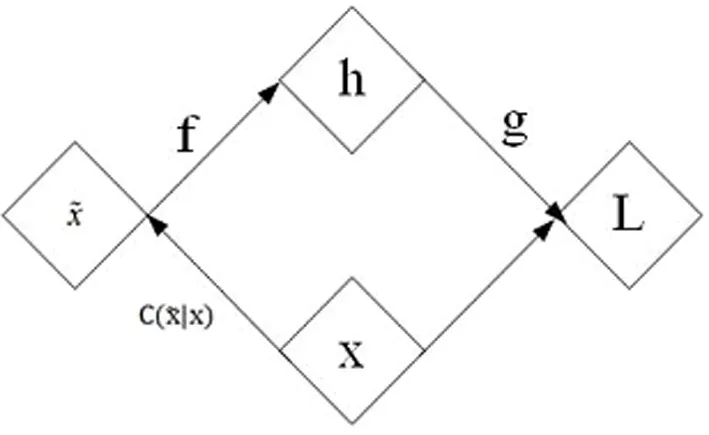
图1 降噪自编码器训练过程

其重构误差函数可由式(3)进行表达。
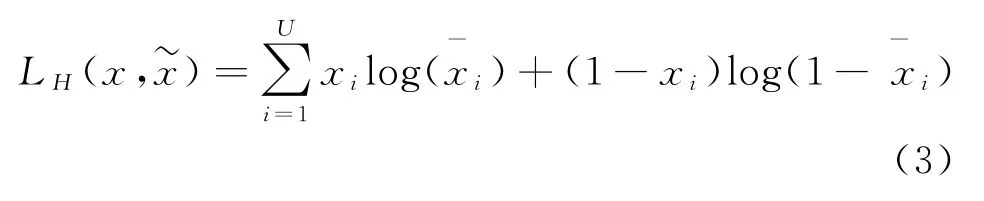
1.4 堆叠降噪自编码器原理
堆叠降噪自编码器主要由三个部分组成:第一,一个编码器;第二,一个解码器;第三,多个降噪自编码器。其原理如图2所示。
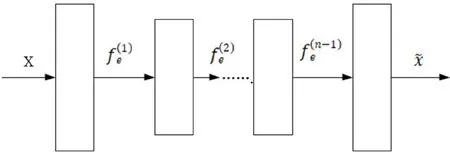
图2 堆叠降噪自编码器原理
堆叠降噪自编码器利用多个降噪编码器对数据进行叠加训练,并依照层级顺序进行非监督学习,充分展现了降噪自编码器的优势,降低了原始数据与输出数据间的损失,增强了算法的推荐效果,使数据能够进行抽象化表达,给出用户偏好预测结果。
2 混合推荐方法
混合推荐方法之所以能够对物品矩阵和用户矩阵进行有效处理,是因其融合了堆叠降噪自编码器和概率矩阵分解,能够通过深度学习法实现物品特征的深层次挖掘,同时能够彰显出其原有的优势,如评分预测等,极大程度提高了推荐算法的鲁棒性。
2.1 混合推荐方法结构设计
混合推荐方法主要由堆叠降噪自编码器和概率矩阵分解这两部分组成,具体如图3所示。
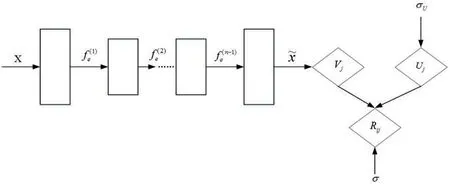
图3 堆叠降噪自编码器结构
堆叠降噪自编码器是由多个降噪自编码器堆叠而成,其可在任意层中进行非监督学习,实现对数据的抽象表达,并在此基础上对用户喜爱物品程度进行预测。同时,还可将其应用于其它场景,如评分预测、文本推荐等。堆叠降噪自编码器首先会将数据传输到其中的降噪自编码器中,其次会利用编码器将其转运至隐层,最后在隐层中实现编码。在概率矩阵分解中,令Rm×n代表用户-物品的评价矩阵,其中,用户个数由n表示,物品个数由m表示。U和V分别代表用户矩阵和物品矩阵,σ2代表方差,那么其表达式如式(4)所示。
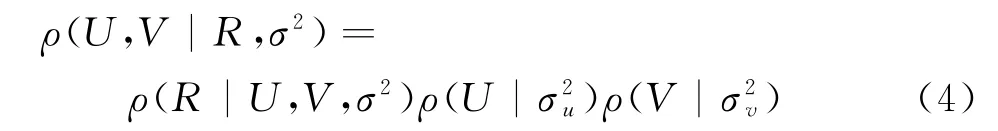
此时,令N μ,σ( ) 代表高斯分布的概率密度函数,Iij代表指示函数,μ代表均值,假如物品j受到了用户i的评价,则用数字1表示其函数值,若未进行评价,那么其函数值则为0。若用户矩阵U与物品矩阵V之间不存在任何关联性,那么R,U,V的概率分布情况如式子5所示。
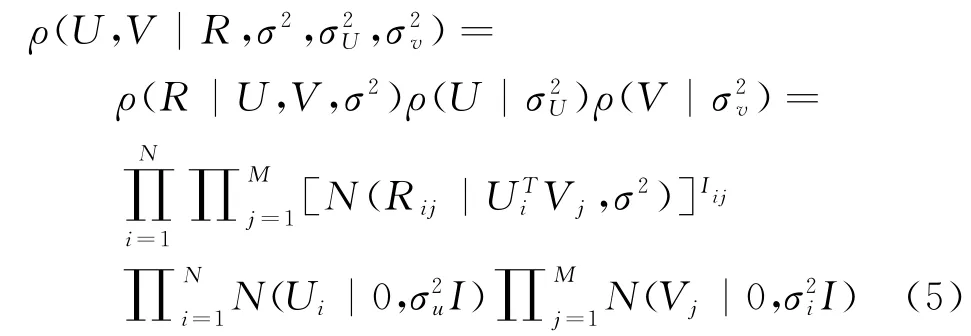
通过以上计算公式可获得最终的预测评分。
2.2 混合推荐方法执行流程
由前文分析可知,混合推荐方法主要由概率矩阵分解法和堆叠降噪自编码器组成。这两种方法相辅相成,既能发挥出原有的优势,如能挖掘出物品深层次特征、给出准确的预测结果等,亦能解决冷启动和数据稀疏这一不足。混合推荐方法训练流程如图4所示。
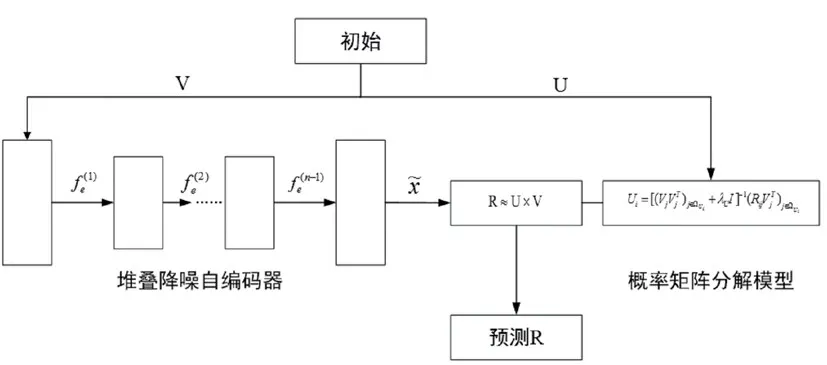
图4 混合推荐方法训练流程
由图4可以看出,混合推荐方法的执行过程主要由概率矩阵分解模型和堆叠降噪自编码器共同完成。其执行流程如下:首先,借助概率矩阵分解方法对评分矩阵R进行转换,使之变成物品特征矩阵V和用户特征矩阵U;其次,将预处理结束后的数据传输至堆叠降噪自编码器中,进行编码和训练,而后解码获取物品特征矩阵V;最后,对矩阵V与矩阵U做乘法运算,运算得到的结果即为用户-物品评分矩阵R。此外,为了提高推荐精度,还可使用乘法将解码得到的隐式特征矩阵V与用户特征矩阵U做运算,以获取最终的预测结果。
2.3 混合推荐方法实现流程
在堆叠降噪自编码器中,通过多个堆叠自编码器的共同作用,第n层的输出转变为第n+1层输出,而后按照顺序训练网络的每一层。初始输入的重构数据源自于最后一层的输出x~ ,该层输出亦可视为概率矩阵分解中的物品矩阵V,使之在矩阵中继续进行推荐。在概率矩阵分解中,通过对用户数据的提炼可得到用户特征矩阵,通过堆叠降噪自编码器可获取物品特征矩阵,而后对这两个矩阵做乘法运算,实现对用户兴趣偏好的预测,并给出最终的推荐结果。混合推荐算法的推荐流程如图5所示。

图5 混合推荐算法推荐流程
由图5可以看出:首先,自编码器会对加噪数据进行训练,经过训练后的数据传输至堆叠自编码器中进行处理,使之解码得到矩阵x~ 。其次,对用户矩阵与物品矩阵进行内积处理,使之成为用户-物品评分矩阵。接着,对该矩阵进行处理,使之成为物品隐式特征矩阵。最后,在概率矩阵中对用户特征矩阵与物品隐式特征矩阵进行内积处理,获取评分矩阵,实现最终的评分预测。
3 实验分析
3.1 实验数据与评价标准
使用的实验数据源自亚马逊Aurora数据库。在该数据集中,边缘视为购买的产品,节点视为产品。通常,推荐系统主要存在两种评判方式:第一种是对用户实际评分与方法预测分数相差的大小进行评判;第二种是对评价预测的精准程度进行预测。经考量,最终选择第一种评判方式作为此次研究的评价标准,即选择均方根误差(RMSE)作为此次试验的评价标准,对预测分数与真实分数间的差值进行评估。
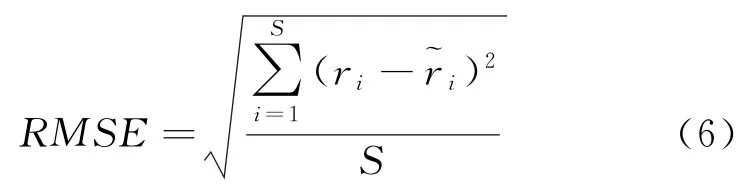
式(6)中,数据集的评分数目由S表示,真实评分与预测评分分别由ri与r~i表示。令用户特征矩阵中均值μ=0,相关超参数隐因子维度k=300。
3.2 实验结果
为了检验混合推荐方法的可行性,利用Aurora数据库收集了两个大小不等的数据集,其相关信息如表1所示。
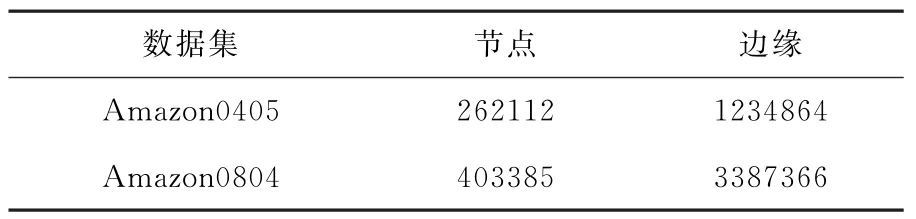
表1 大小不等的数据集信息
为了更好体现混合推荐方法的可行性,与概率矩阵分解、降噪自编码器+概率矩阵分解这两种方法进行了比较分析,不同推荐算法的实验结果如图6所示。
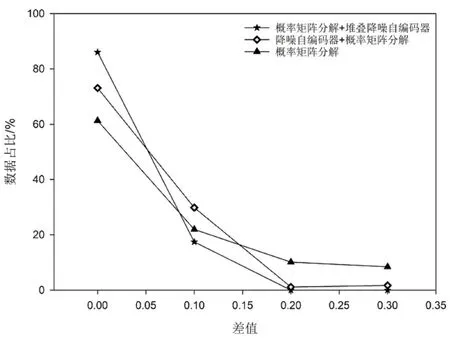
图6 不同推荐算法推荐结果
图6中,横坐标的数据为原始数据与预测数据间差值的绝对值,纵坐标所给出的数据意义为差值在所有数据中的占比。从数据占比来看,提出的混合推荐算法效果明显优于其他两种推荐算法。从差值情况来看,提出的混合推荐算法占比最小。三种推荐算法之中,概率矩阵分解法不论是数据占比还是差值均处于末位。综上可知,提出的混合推荐算法是可行的,拥有较高的预测精度。
4 结 语
综上,首先对推荐方法的原理进行了简要概述,为后文的写作奠定了理论基础。其次,将堆叠降噪自编码器与概率矩阵分解法相结合,提出一种混合推荐方法,并给出混合推荐算法的执行过程和实现流程。最后,通过实验对比发现,所提的混合推荐算法在数据占比和差值比较方面均优于其他两种传统推荐算法,能够提高推荐精度,证明了该算法的可行性和有效性。

