水下航行器流场特性与辐射噪声数值研究
张卿冕,肖正明
(昆明理工大学 机电工程学院,昆明 650500)
某水下航行器主要用于攻击敌方的水面和水下目标,也用于封锁航道和港口。因此研究水下航行器周围复杂流场有着重要的意义[1-2]。当水下航行器在水下航行时,特别是在搜索和跟踪目标的过程中,为了避免被敌人过早发现,必须保持自身的安静性和隐蔽性[3-4]。
翟朔等[5]采用数值计算方法,对比了在艇体边界层条件影响下两种不同的舵翼组合方式的水动力性能和尾流特征。Mogan等[6]针对两艘潜艇获得了阻力,推力和功率的初步计算。张大朋等[7]运用Gertler和Hargen运动方程来描述拖曳体的水动力状态,探索了不同参数对水下拖体的影响。漆小舟等[8]对万米水下机器人,在不同漂角和攻角工况下进行了数值模拟,计算得到了部分水动力系数。PAN等[9]利用数值方法评估潜艇的机动特性,使用RANS求解器计算流体动力和力矩。
航行器的噪声辐射是航行器自噪声的主要组成部分,它所形成的声纳背景噪声将掩盖来自远距离目标声信号的接受。因此,研究航行器所辐射的噪声具有十分重要的意义。文献[10-11]利用边界元法(BEM)预测潜艇的噪声,通过边界积分方程的解将压力分散在壳体表面上,而在流体域中辐射的噪声由相应的边界积分表示。Özden等[12]主要通过数值计算螺旋桨辐射噪声,使用CFD软件解决了螺旋桨周围的流动问题。李清等[13]聚焦1~100 Hz低频段下的舰船水下机械辐射噪数值计算,探讨了流固耦合与声固耦合动力学方程的等效性条件及两者差异。徐园园等[14]基于声散射模型分析了高频段,高航速条件下鱼雷辐射的噪声级。王凯等[15]基于CFD计算了离心泵内部瞬态流场,提取其全级数壁面偶极子声源,并采用直接边界元法计算泵内流体诱导噪声。
综上所述,以上参考文献没有研究不同工况下航行器鼻端压力的变化规律,没有对航行器在各工况下声功率级的变化以及声场中各点在轴向上的声压变化进行规律的探讨,并且没有研究声场中轴向各点在不同频率下声压值与距离的关系。
本文以流体仿真软件分析模拟了航行器的流场特性,得到了不同工况下航行器鼻端压力随时间的变化;以壳体的压力脉动作为偶极子声源,采用直接边界元法计算噪声辐射,提取了航行器在不同来流速度和不同水压下场点的声功率级曲线;通过设置探测器,观测探测器的声压大小及变化规律。在声场设置12个特征点,观察声场中轴向各点在不同频率下声压值随距离的变化规律。
1 计算方法
1.1 控制方程
在湍流得非直接数值模拟中,Reynolds Navier-Stokes方程应用最广泛。用张量的指标形式表示的时均连续方程、Reynolds方程如下[16]:
(1)
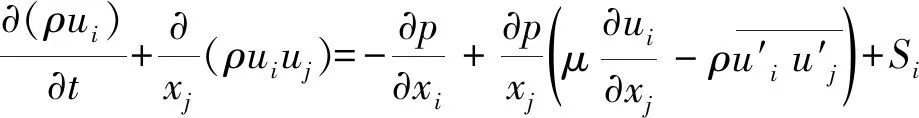
(2)
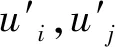
1.2 湍流模型
在计算过程中,湍流模型采用SSTk-ω两方程模型,相应的k方程和ω方程分别为:
(3)
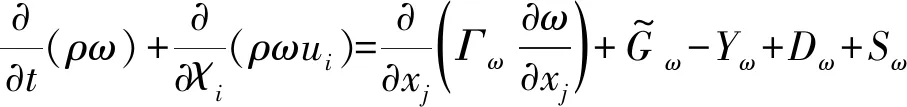
(4)
式中:k表示湍动能;ω表示特别耗散率,可以认为是湍动能扩散率ω和湍动能k的比值;Γk和Γω分别代表k和ω的有效扩散;Yk和Yω分别代表k和ω的耗散;Gk代表k的产生项;Gω代表ω的产生项;Dω是交叉扩散项;Sk和Sω是自定义源项。
1.3 声学边界元方程
对于航行器直接辐射噪声,由于在低马赫数下,四极子声源的影响很小,此时偶极子声源是最主要的[17]。因此,仅考虑偶极子声源作为边界条件,将壁面压力脉动转移到声学网格上进行求解。结构外部单频声场的Helmholtz积分方程为
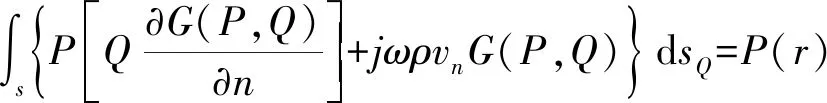
(5)

Bp=Cvn
(6)
式中:B和C为边界元法的系数矩阵;p为节点声压向量;vn为节点法向速度向量。
2 流场特性分析
2.1 计算模型
本文采用的模型是由一个壁厚30 mm轴对称体、4个尾翼和共轴对转螺旋桨组合而成,共轴对转螺旋桨是由前桨和后桨组成,航行器的总长L为4 m,口径为0.5 m,4个尾翼为对称翼型,翼后缘位于3.2 m处,螺旋桨是由4个桨叶和中央桨毂组成,桨毂直径为0.18 m,数值计算模型如图1所示。

图1 数值计算模型
2.2 边界条件与网格划分
因采用的水下航行器模型为圆形截面的回转体,创建R=5 m的外流域,其长度为航行器总长的5倍,流域轴线与航行器纵向一致。
建立直角坐标系,原点位于航行器首部最前缘,x轴正方向指向航行器尾部,z轴正方向指向围壳,y轴正方向按右手法则进行定义。计算域边界的设置如下:
1) 速度入口(Inlet)。它为距航行器首部最前缘2L处的圆端面,u=U,v=w=0,其中U为来流速度。
2) 压力出口(Outlet)。它为距航行器尾部2L处的圆端面,选用压力出口边界类型,设定相对于参考点的流体静压值。
3) 远场边界 (Free slip wall)。它为距航行器对称轴与航行器等长的圆柱面,其类型为移动壁面,设置壁面移动速度与入口来流速度的大小和方向相同。
4) 物面边界 (No slip wall)。它为航行器的表面,选用无滑移壁面边界类型,即u=v=w=0。
外流域与边界设置如图2所示。
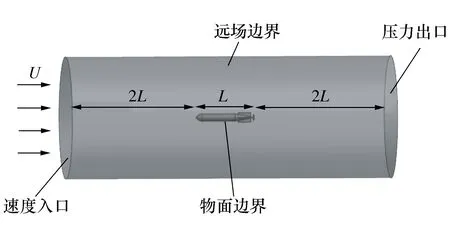
图2 外流域与边界设置
采用以多面体为核心的切割体网格和棱柱层网格对计算域进行离散。通过插入块功能模块对相应的区域进行局部加密,以便更好地捕捉流动细节。划分网格时在水下航行器的周围设置了5层棱柱层,且棱柱层的总厚度不能小于15 cm,有利于捕捉流体边界附近的流动特性,获得更加精确的流场信息,最终生成网格数约190万。设置一个对称面,更好的显示加密区和棱柱层,网格具体划分情况如图3所示。

图3 对称面上的网格分布
2.3 航行器的流场仿真计算
网格划分后,设置物理模型,依次选择隐式不定常、液体、分离流、恒密度、湍流模型,在水深为40 m,来流速度分别为30 kn,40 kn和50 kn,计算得出航行器在不同来流速度工况下阻力系数变化曲线,如图4所示。
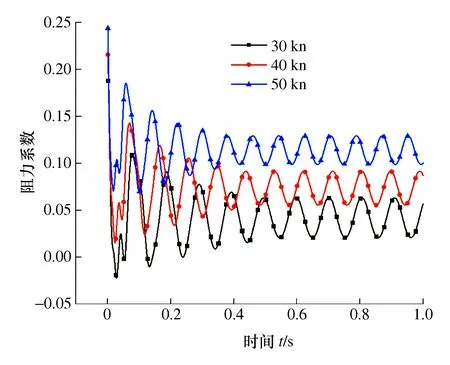
图4 阻力系数
由图4可以看出:不同来流速度下阻力系数的变化趋势一致,都是呈现减小趋势,且慢慢趋于稳定波动,收敛效果较好。来流速度在50 kn所受阻力最大,30 kn最小;整体来看,来流速度越大,航行器受到的阻力越大。
为了更好的观察航行器表面压力的分布,分别提取了3个来流速度工况下航行器表面压力云图,如图5所示,不同来流速度下最大压力出现的位置相同,且都出现在航行器鼻端处、4个尾翼前端和螺旋桨的浆叶上,随着来流速度的增大,航行器受到最大压力增大,最小压力都出现在螺旋桨桨叶背面。
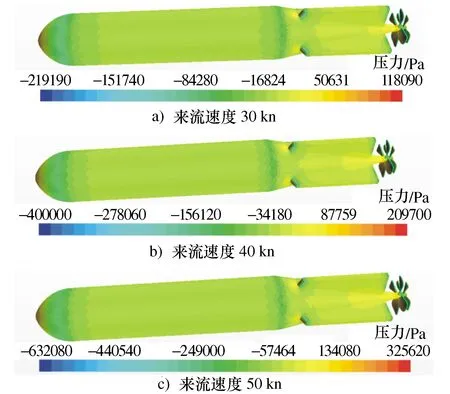
图5 不同来流速度下航行器表面压力云图
在航行器的鼻端处设置一个数据点,点零部件在区域中的一组坐标下对其输入零部件进行采样,使用包含区域和边界的父零部件创建点零部件,通过输入点坐标(0,0,0),可以指定点位置,数据点的设置如图6所示。

图6 数据点的设置
图7为3个来流速度下数据点的压力变化,可以看出,3个来流速度下,数据点都是在起始时受到的压力略大,呈现减小趋势,最终趋于稳定波动,收敛效果较好,在来流速度为50 kn时,数据点所受的压力峰值最大,30 kn最小,随着来流速度的增大,航行器的鼻端受到的压力增大。

图7 不同来流速度下数据点的压力变化
满足航行器的结构刚度,刚性等要求,在同一来流速度下,适当改变航行器的航行深度,来观察不同水深对数据点所受压力的影响,图8为不同水深下数据点压力的变化,在起始时,数据点的压力值较大,变化趋势大致相同,呈逐渐减小趋势,最后趋于稳定波动。从图8中可以看出在水深50 m峰值最大,水深30 m最小。航行深度越深,数据点所受到的压力越大,从而航行器鼻端所受到的压力越大,最后压力波动情况趋于稳定。
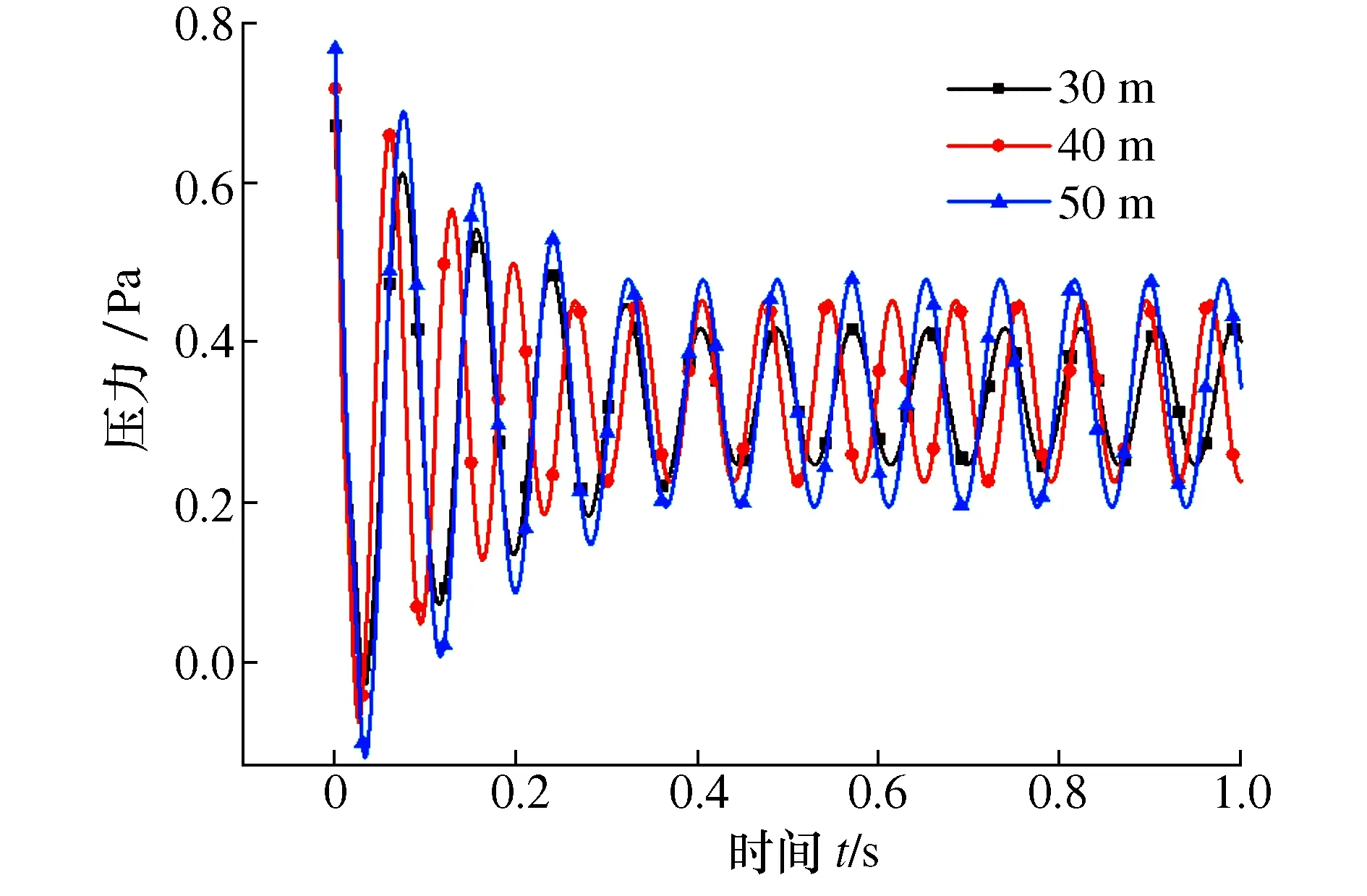
图8 不同水深下数据点的压力变化
图9给出了来流速度为40 kn时航行器的速度变化云图,由于设置了固壁边界条件,壁面的速度均为零,航行器鼻端、尾翼前端和螺旋桨尾流部分的速度小于其它区域。还可观察到螺旋桨存在对于流场的影响,产生的尾流延伸到了尾部较远的地方,这也表明本文的计算较好地捕捉到了流场流动的细节。

图9 40 kn时航行器的速度云图
3 航行器辐射噪声计算与分析
3.1 航行器辐射噪声仿真环境
导出在流体软件中计算的壳体压力脉动,它包含壳体的网格数据、物理变量以及存储结构,通过相关接口导入到声学计算软件中,设置声学边界元环境,在结构网格上插入声学网格,声学网格必须保证一个波长之内有6个节点,这样才能保证计算精度,同时又减小计算量。压力数据通过FFT将时域转化为频域,将偶极子声压等效为声压边界条件,作为辐射噪声源。建立9 m×4 m声学采集面(面场点),便于观察水平方向上的声压变化。其外声场边界元模型如图10所示。以来流速度40 kn下的压力脉动为激励,取流体为海水,水深40 m,海水密度ρ=1 025 kg/m3,声音传播速度c=1 500 m/s,航行器材料为钢(弹性模量E=2.1×1011Pa,泊松比μ=0.3,密度ρ=7 850 kg/m3),计算起始频率为1 Hz,终止频率为4 000 Hz,进行航行器辐射噪声的计算。

图10 外声场边界元模型
3.2 航行器辐射噪声数值计算结果
求解非定常流动中的航行器辐射噪声,计算精度取决于面场点的流场和声学边界处理,通过无能量损失映射算法将壁面脉动压力转移到声学网格上,仿真计算得到各频段声压云图如图11所示。
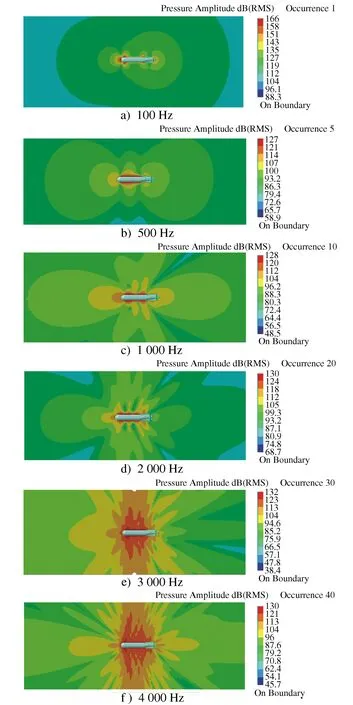
图11 声压云图
从各频率下声压云图可以看出,由于考察对象的对称性,声压云图也呈上下对称显示,频率越高,声压在场点上的分布越不规则,其场点的声压值集中在35~170 dB之间,100 Hz频率下的声压值较其它频率下的声压值大,航行器侧部辐射噪声声压值要高于航行器头部和尾部辐射噪声声压值。
图12给出了3种来流速度工况下航行器结构水下辐射场点声功率级对比曲线。从图12中可看出,3种工况下的声功率级在低频段呈上升趋势,宽频段和高频段下的声功率级在稳定范围内上下波动,来流速度为50 kn的声功率级最大,来流速度为30 kn的声功率级最小,可得出结论,来流速度增大,航行器结构的辐射声功率级越大。
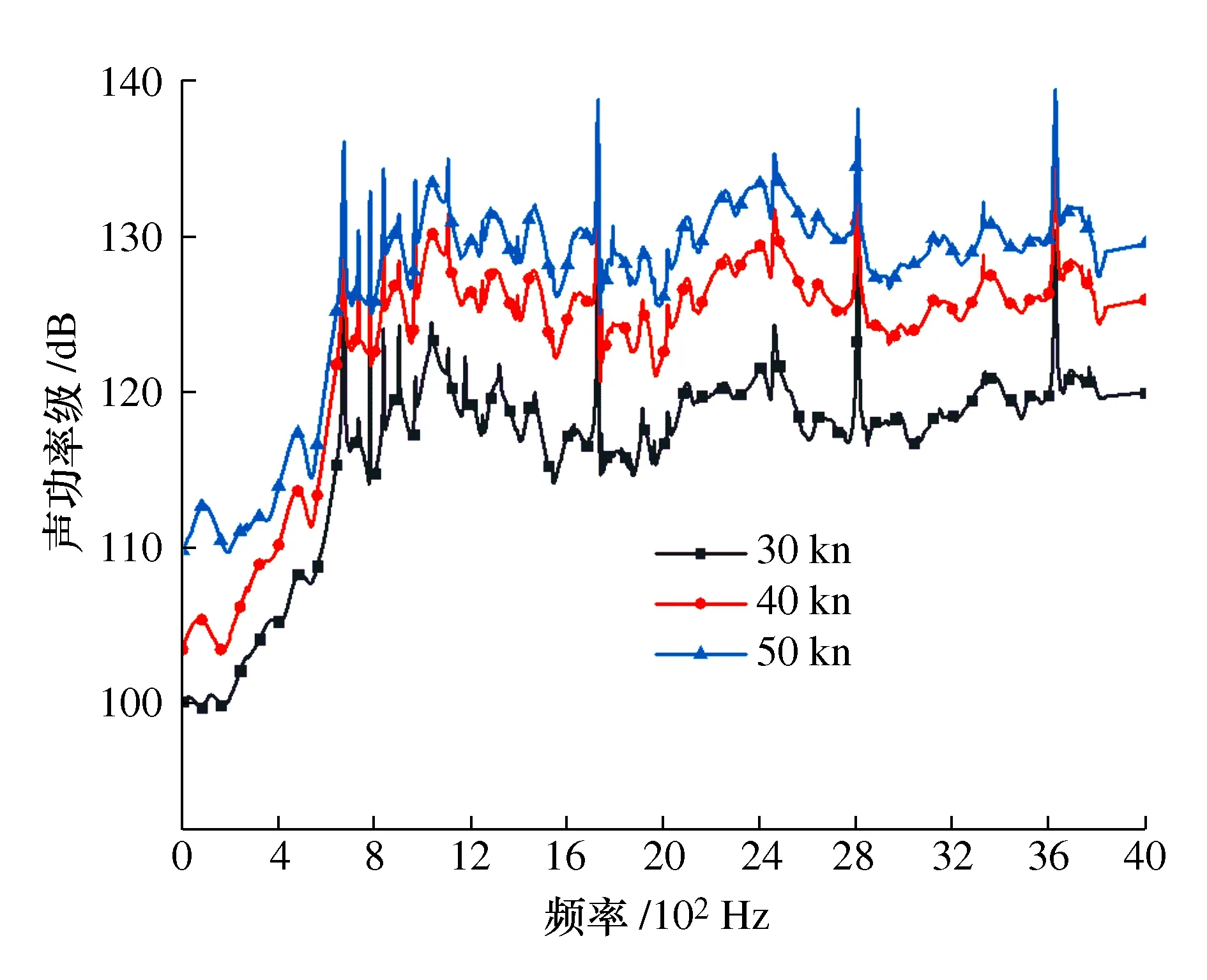
图12 不同来流速度下场点声功率级频谱
图13所示为不同水深下航行器结构辐射场点声功率级曲线,在水深50 m声功率级最大,水深30 m时声功率级最小,所以水压越大,则辐射声功率级越大。
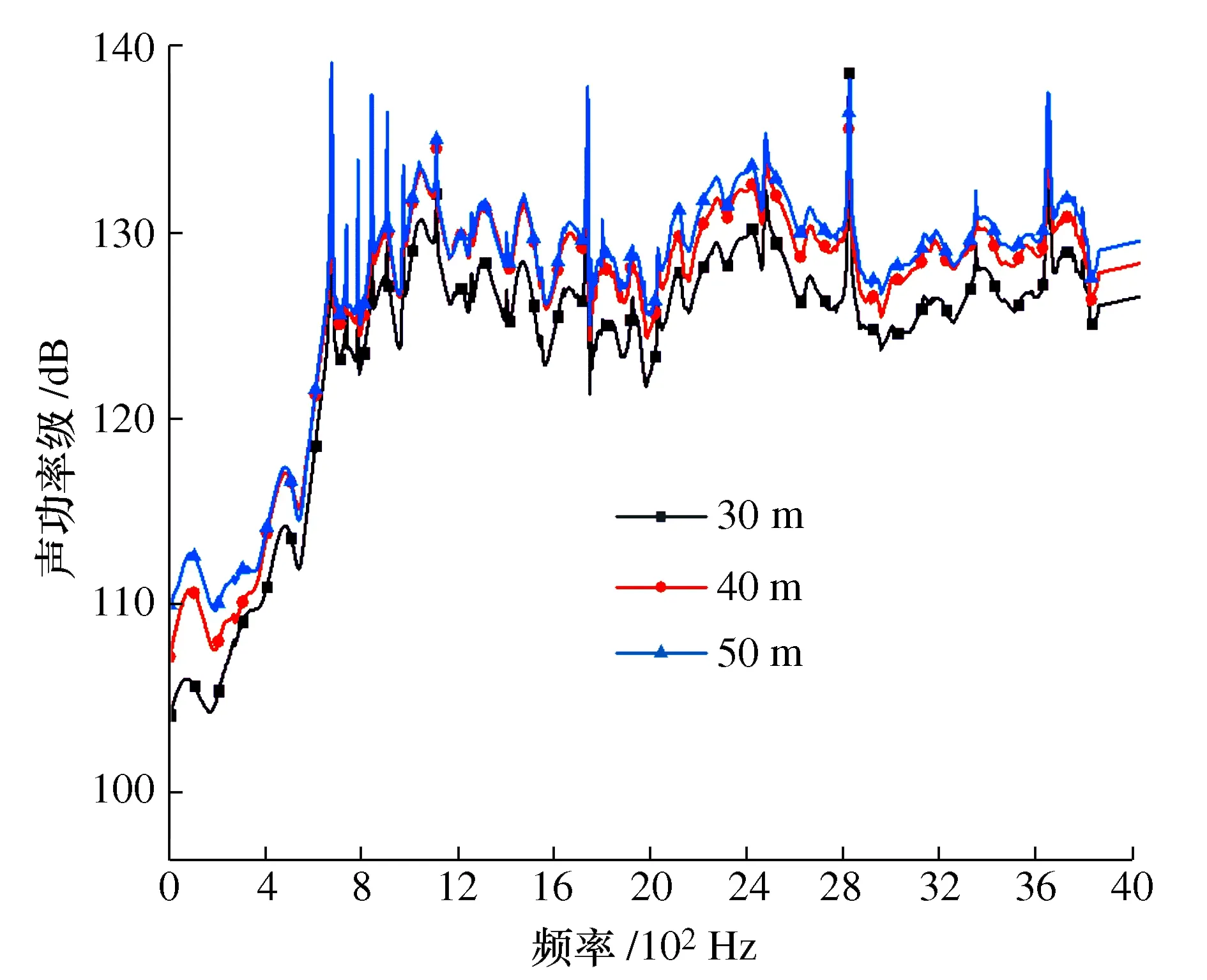
图13 不同水深下面场点声功率级频谱
在场点上设置探测器,如图14所示,可清晰的探测出声场中轴向各点的声压大小及变化规律。讨论航行器在40 kn来流速度下,壳体辐射噪声沿x轴变化规律,获得各探测器的声压频谱特性,如图15所示。
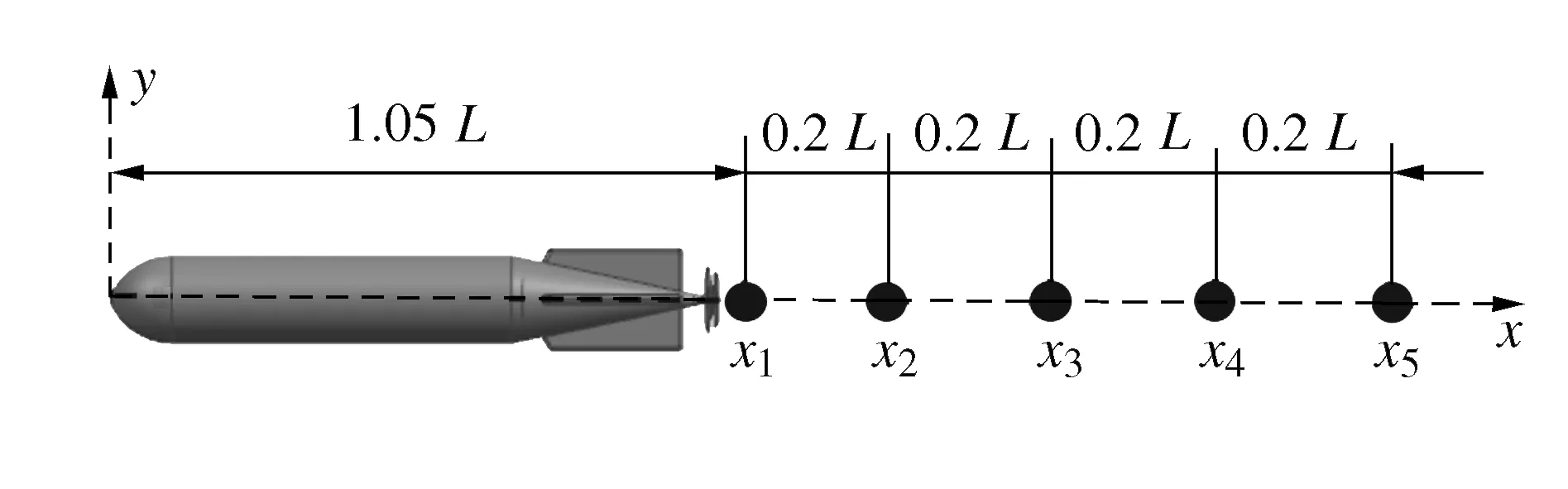
图14 探测器安装位置示意图
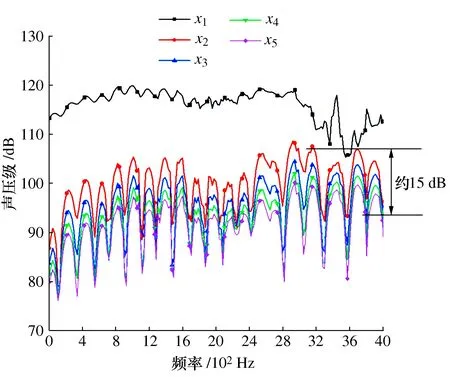
图15探测器声压级频谱曲线
图15给出了5个探测器声压级频谱图,从图中可看出,由于探测器x1距离航行器最近,此处噪声辐射的声压级最大,这也间接的说明航行器附近流场导致的噪声最大,随着探测器与航行器之间的距离的增大,声压级越小,探测器x5距离航行器最远,此处噪声最小。探测器x2~x5相比探测器x1声压级波动较大,且极大值比极小值高约15 dB,当来流速度较高时,水流激烈冲击航行器舷外附体,导致附体后方产生大量涡旋,涡旋每次从附体脱落,都会产生环量,导致作用于附体的横向力不平衡,迫使附体振动,产生能量很强噪声,探测器的声压级在频段中就会出现波动较大的极值。
坐标系的建立如图14所示,在螺旋桨正后方(x轴)取12个特征点,观察各特征点在不同频率下声压值随距离的变化,第1个特征点的横坐标x=1.05L(L为航行器长度),纵坐标y=0,随后每个特征点之间的距离为0.2L,第12个特征点的坐标为x=12.8 m,y=0,其频率在100 Hz、500 Hz和1 000 Hz下各特征点声压值与距离的关系曲线如图16所示。

图16 特征点处的声压值
从图16中可以看出,3个频率下特征点的声压值在近场区域下降的较快,距离越大,曲线下降的斜率迅速减小,说明航行器的辐射噪声在近场区域衰减的速度较快,3个工况下,频率为100 Hz时,特征点的声压值最大,1 000 Hz时,特征点的声压值最小。
4 结论
本文基于流体分析软件对航行器在不同工况下的流场进行了数值模拟,得到壁面压力脉动作为声学激励源,采用直接边界元法(BEM),仿真计算了辐射噪声,得出了以下结论:
1) 通过对航行器流场数值分析,得出航行器的阻力系数随来流速度的变化规律。通过分析数据点所受压力随不同航速和不同水深的变化,从而得出航行器鼻端压力的变化规律。比较了不同来流速度下航行器压力云图,来流速度越大,压力越大。
2) 由声压云图可看出,在100 Hz频率下的噪声较其他频率下的噪声大。分析了不同来流速度下面场点声功率级的变化,得出随着来流速度的增大,航行器结构的辐射声功率级增大。改变航行器的航行深度,来观察在不同水压下对辐射噪声的影响,水压越大,则辐射声功率级越大。通过设置探测器来观测场点中各点的声压级变化,距离航行器最近的点,其噪声辐射的声压级最大,辐射噪声值在近场区域衰减的速度较快。

