控制图经济设计的随机梯度优化方法

张公伯 彭一杰 杨书淮

摘 要：控制图作为一种实施统计过程控制的工具，在现代制造业的质量管理中具有广泛应用。控制图的经济设计可以提高过程控制效率，降低过程控制成本。本文提出一种基于随机梯度估计的控制图经济设计优化方法，首先应用广义似然比法估计平均运行成本的梯度，并分别结合逐步增加仿真样本量和随机化仿真样本量的随机近似方法得到控制图的最优控制上界。最后，重点展开介绍了本文提出的控制图经济设计方法在休哈特控制图和指数加权移动平均控制图中的应用。

关键词：控制图;随机梯度估计;广义似然比法;随机近似

中图分类号：F273.2文献标识码：A文章编号：2097-0145（2022）03-0045-08doi：10.11847/fj.41.3.45

Stochastic Gradient Method for Economic Design of Control Charts

ZHANG Gong-bo1， PENG Yi-jie1， YANG Shu-huai2

（1.Guanghua School of Management， Peking University， Beijing 100871， China; 2.College of Engineering， Peking University， Beijing 100871， China）

Abstract：As a tool for statistical process control， control chart has been widely used in quality management in modern manufacturing. The economic design of a control chart can improve the efficiency and lower the cost of process control. This paper proposes a gradient-based simulation optimization method for economic design of control charts. In the first part， the generalized likelihood ratio method is used to obtain the gradient estimate of the average running cost. Then two stochastic approximation methods with increasing sample size in iterations and randomized sample size are utilized respectively to obtain the optimal upper control limit. In the end， the paper applies the proposed method to Shewhart and exponentially weighted moving average control charts.

Key words：control chart; stochastic gradient estimation; generalized likelihood ratio method; stochastic approximation

1 引言

當今世界正高速迈入以数字化、智能化为特点的新阶段，人们对产品和服务质量的重视程度不断提高。统计过程控制作为一种应用统计方法对生产和服务过程进行评估和监控，从而保证产品和服务符合规定要求的质量管理技术，已广泛应用于制造业和服务业。控制图是一种实施统计过程控制的工具，它是基于系统运行中测定的关键特性值，通过绘制相应的系统特性值统计图，并根据假设检验原理判断系统是否处于控制状态的统计图形方法。控制图的概念最早由休哈特[1]提出，在统计过程控制领域中备受学界和业界关注。近年来，控制图广泛应用于集成电路制造[2]、医学与流行病学[3]、畜牧业养殖管理[4]、铁路接触网检测[5]和临床化学质量控制[6]等领域。

系统平均运行长度（Average Run Length， ARL）是普遍使用的控制图统计性评价指标，它是系统偏移或宣告失控前所需要的平均观测周期数。蒙特卡洛仿真、积分方程和马尔可夫链方法可以估计控制图的平均运行长度[7]。对控制图进行优化设计和敏感性分析是统计质量控制中具有挑战性的问题。受生产人员、机械设备、生产环境和原材料等因素的影响，生产过程会突发故障处于失控状态，将影响制造产品的质量，导致产品异常损耗及故障维修成本。控制图的参数设计往往会影响样本的抽样和检测、生产过程异常排查及维修等控制措施的成本。在控制图统计性质的基础上，需要考虑控制图的经济设计，在提高控制图监控效率的同时，降低监控过程产生的成本，维持生产过程处于受控状态，减少制造阶段因产品异常带来的损失，提升控制图的经济效益。Lorenzen和Vance[8]提出了一种静态控制图经济设计的成本函数模型。有关可变抽样区间和可变样本容量的动态控制图经济设计的研究，可参考文献[9～11]。这些研究往往通过马尔科夫链方法估计控制图的平均运行长度，采用遗传算法等启发式算法优化成本目标函数求解最优设计参数。

控制图的优化问题属于复杂随机系统优化问题，其目标函数的解析表达通常未知且含有大量系统设计变量。蒙特卡洛仿真得到的系统样本表现可以估计目标函数。梯度包含了目标函数随参数变化的信息，在迭代搜索优化算法和敏感性分析中有着重要的应用。通过蒙特卡洛仿真估计的随机系统中目标函数关于参数的梯度称为随机梯度估计。常用的无偏随机梯度估计方法有无穷小扰动分析法[12]，似然比法[13]和弱导数法[14]。无穷小扰动分析法无法解决样本表现不连续的问题，而似然比法和弱导数法无法解决样本表现带有结构参数（出现在样本路径与系统表现度量的函数关系中的参数）的问题。控制图的控制边界属于结构参数，且蒙特卡洛仿真得到的系统样本表现关于控制边界不连续，无法保障常用的随机梯度估计方法的无偏性。Peng等[15，16]提出的广义似然比法为无偏随机梯度估计，该方法既适用于带有结构参数和不连续的样本表现的问题，同时具有无偏性和单样本轨道性。A67D4071-5767-49FE-868D-67CB7CFF2701

采用随机梯度估计方法优化设计控制图的现有研究具有局限性。Lele[17]采用有限差分法分别估计指数加权移动平均和贝叶斯控制图的梯度，但有限差分法得到的梯度是有偏的，且需要选取摄动值的大小，在处理高维参数向量时需要很大的计算量。Fu等[18，19]采用平滑扰动分析法得到指数加权移动平均控制图的无偏梯度估计和控制图经济设计的最优控制边界，但平滑扰动分析法需要解析地计算一个条件期望，在实际应用中需要视控制图的设定而选取适当的条件。Peng等[15，16]采用广义似然比法得到指数加权移动平均控制图的无偏梯度估计，但没有考虑控制图的经济设计问题。本文提出一种考虑过程平均运行长度和控制成本的控制图经济性评价指标，并提出一种基于随机梯度估计的控制图经济设计方法。本文首先采用广义似然比法估计控制图平均运行成本的梯度，解决了常用的随机梯度估计方法不适用及需要取条件期望的问题，提供了成本目标函数随控制图设计参数变化的梯度信息，丰富了对控制图进行经济优化设计的方法。进而考虑服从正态分布和均匀分布的质量特性值，通过逐步增加仿真样本量和随机化仿真样本量的随机近似方法得到控制图经济设计的最优控制边界，同时讨论了两种随机近似方法的理论性质。并以休哈特（Shewart）和指数加权移动平均（Exponential Weighted Moving Average， EWMA）控制图的应用为例，说明提出方法的有效性。

2 问题构建

考虑包含单个可测的系统过程变量的控制图，其中系统过程变量具有稳定的受控状态和不稳定的失控状态。系统失控时间τ不可观测，其累积分布函数为F0。控制图的采样间隔时间为Δ。在每个采样点，可以观测到系统的检验统计量：Y1=X1;Yi=（Xi，Yi-1;θ），i>1，其中θ∈Θ为控制图设计参数，Xi为第i个仿真输出的质量特性值，是与系统参数无关的马尔可夫链的转移函数。系统处于稳定的受控状态时，Xi的累积分布函数为F1;系统处于不稳定的失控状态时，Xi的累积分布函数为F2。

例1 休哈特控制图：Yi=Xi，i1。

例2 指数加权移动平均控制图：Y1=X1;Yi=αXi+（1-α）Yi-1，i2，0<α1。

令θ1，i和θ2，i分别为第i个检验统计量的控制下界和控制上界。控制图的设计参数为控制界限：θ=θ1，i或θ=θ2，i。当检验统计量Yi偏移至控制界限之外时，判定系统处于不稳定的失控状态。判定系统處于失控状态的时间为：

N=min{i：Yi[θ1，i，θ2，i]}，即检验统计量Yi不在控制界限内的停时，是一个离散型随机变量。控制图的平均运行长度是判定系统处于失控状态的时间的期望，即

ARL（θ）=E[N]

=∑∞n=1nPr（N=n）=∑∞n=1nE[1（N=n）]（1）

其中1（·）为示性函数，Pr（·）为括号中事件发生的概率。ARL（θ）作为控制图的一种统计性评价指标，没有考虑成本等经济因素。如下提出一种考虑系统在失控状态下的产品损耗及判定系统处于失控状态时的维修成本的控制图经济性评价指标。假设系统处于不稳定的失控状态时，由于制造流程出现异常，生产产品的质量无法得到保障，每单位时间支付损耗成本c;当判定系统处于失控状态时，需一次性支付系统维修成本C。当系统完成维修时，系统会恢复正常运行状态，因此，该过程可以视为一个再生过程。每进行一次循环，该过程的成本期望值为：cE[（N-「τ/Δ）+]+C，其中「x为向上取整函数;若x0，（x）+=x，反之，（x）+=0。单位时间内的平均运行成本可以表示为

C（θ）=cE[（N-「τ/Δ）+]+CE[N]

C（θ）是一种控制图的经济性评价指标。可以观察到，增大控制图的控制上界与控制下界之间的距离会导致判定系统处于失控状态的频率降低，从而减少一次性维修成本;但同时会增加系统处于不稳定的失控状态的时间，导致更大的单位时间产品异常成本。因此，优化设计最优的控制界限可以实现产品损耗成本与系统维修成本的平衡。在给定产品损耗成本c、系统维修成本C的条件下，通过优化设计控制图的控制界限θ，达到极小化单位时间的平均运行成本C（θ）的目标，即θ*=arg minθC（θ）。随机近似方法是一种基于梯度的参数优化方法，适用于优化求解高维参数。本文采用随机近似方法搜寻控制图的最优控制界限θ*。参数的第k次迭代可以表示为：

θ（k+1）=θ（k）+αkC^k（θ（k）），其中αk为第k次迭代的步长，C^k（θ（k））为C（θ）/θ|θ=θ（k）的估计量

C（θ）θ=cE[（N-「τ/Δ）+]θE[N]-（cE[（N-「τ/Δ）+]+C）E[N]θ（E[N]）2

注意到C（θ）/θ的计算中包含E[N]/θ和E[（N-「τ/Δ）+]/θ。记E[N]/θ=E[G1（θ）]，E[（N-「τ/Δ）+]/θ=E[G2（θ）]。由于通过仿真得到的N关于控制图的控制界限θ不连续，无穷小扰动分析法、似然比法和弱导数法均不适用。本文采用的广义似然比估计法可以在仿真N的同时，分别得到随机梯度的单样本无偏估计量G1（θ）和G2（θ）。将仿真得到的估计量代入C（θ）/θ中，得到梯度估计C^k（·）

C^k（θ）=c∑ki=1G2，i∑ki=1ni-（c∑ki=1（ni-「τ/Δ）++kC）∑ki=1G1，i（∑ki=1ni）2

C^k（·）是由若干估计量构成的非线性函数，通常不是C（θ）/θ的无偏梯度估计量。梯度估计

C^k（·）与真实梯度C（θ）/θ之间的偏差可以通过增加仿真样本数量的方法进行消除，即满足渐近无偏性：limk→∞ E[C^k（θ）]=C（θ）/θ。

3 基于广义似然比法的无偏梯度估计

本节给出当仿真输出的质量特性值Xi分别服从正态分布和均匀分布时，采用广义似然比法得到的E[N]/θ和E[（N-「τ/Δ）+]/θ的单样本无偏梯度估计量。A67D4071-5767-49FE-868D-67CB7CFF2701

3.1 质量特性值服从正态分布的广义似然比估计量

假设质量特性值Xi处于稳定的受控状态时，服从均值μ1，方差σ21的正态分布;质量特性值Xi处于不稳定的失控状态时，服从均值μ2，方差σ22的正态分布。（1）式中的N可以改写为

N=min{i：Yi[θ1，θ2]}

=min{i：gi（X1，…，Xi;θ）[0，1]}

其中gi（X1，…，Xi;θ）=（Yi-θ1）/（θ2-θ1），i1。则1（N=n）=（∏n-1i=11（0gi（X1，…，Xi;θ）1））×（1-1（0gn（X1，…，Xn;θ）1）），∏0i=11。取条件于τ/Δ=z，Xi的条件概率密度为：

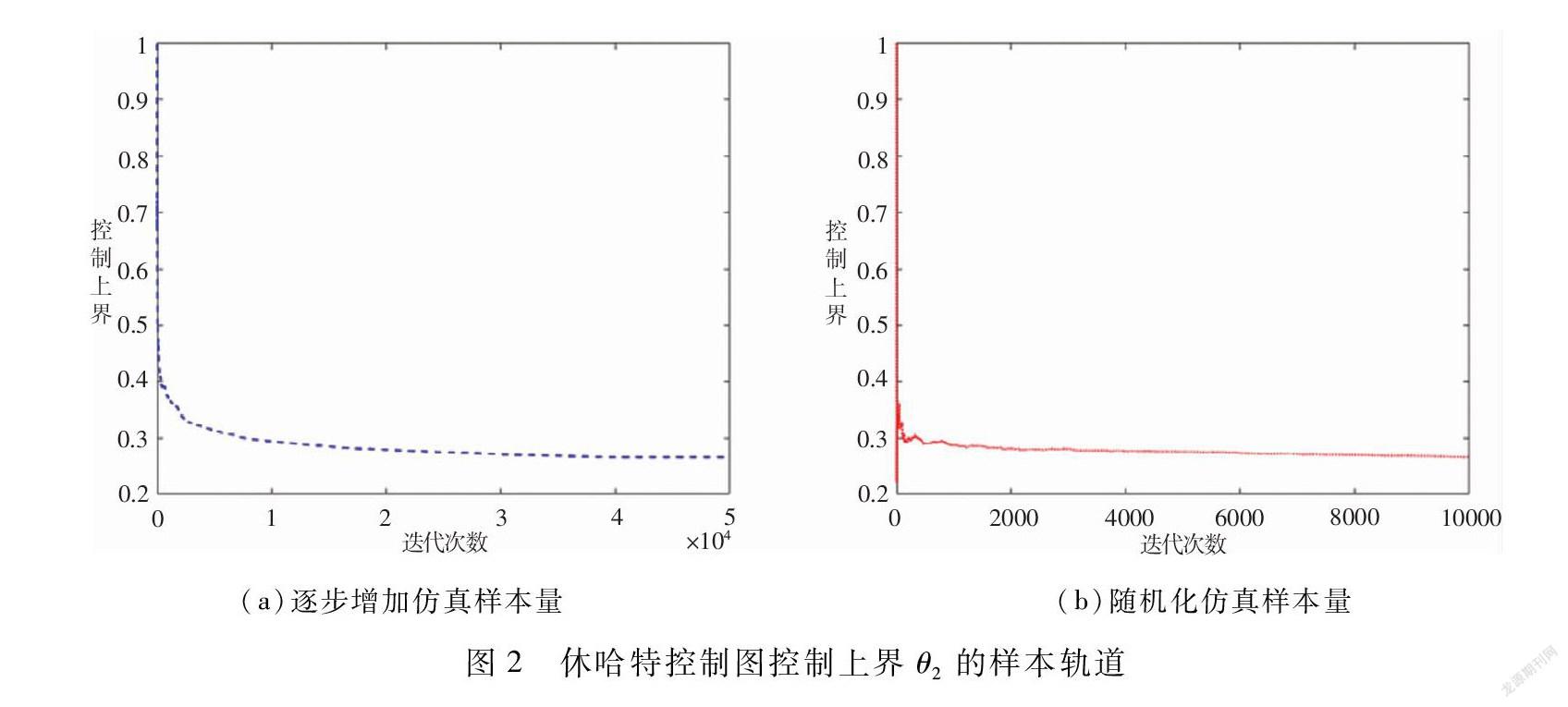
fi（xi|z）=1（i

记Jg（x（n）;θ）g（x（n）;θ）为g（g1（x1;θ），g2（x1，x2;θ），…，gn（x1，x2，…，xn;θ））′的雅克比矩阵。如果Jg（x（n）;θ）是可逆矩阵且g（x（n）;θ）二阶连续可微，采用广义似然比法得到

E[N]θ=∑∞n=1nE[1（N=n）]θ=∑∞n=1nE[1（N=n）w（X（n）;θ）]

其中w（X（n）;θ）=lnf（x（n）;θ）/θ+d（x（n）;θ）。d（x（n）;θ）=∑ni=1（J-1g（x（n）;θ）xiJg（x（n）;θ）J-1g（x（n）;θ）ei）′θg（x（n）;θ）-tr（J-1g（x（n）;θ）θJg（x（n）;θ））-（θg（x（n）;θ））′J-1g（x（n）;θ）x（n）ln f（x（n）;θ）。

qJg表示对Jg矩阵中与q有关的元素求导数，ei为第i个元素为1的单位向量，tr表示矩阵的迹。

x（n）ln f（x（n）;θ）=（ln f（x（n）;θ）/x1，…，ln f（x（n）;θ）/xn）′

=-（xi-μ1σ211（i

采用广义似然比法分别得到E[N]/θ和E[（N-「τ/Δ）+]/θ的单样本无偏梯度估计量为：Gnormal1（θ）=N×w（X（n）;θ），Gnormal2（θ）=（N-「τ/Δ）+×w（X（n）;θ）。

例3 考虑常数的控制图界限，即：θ1，i=θ1，θ2，i=θ2。在给定控制图的控制下界θ1的条件下，优化设计控制图的控制上界θ=θ2。当仿真输出的质量特性值Xi服从正态分布时，对于指数加权移动平均控制图，

w（X（n）;θ）=Nθ2-θ1-（θg（x（n）;θ））′J-1g（x（n）;θ）x（n）ln f（n）（x（n）;z）|n=N，x（n）=X（n），其中θg（x（n）;θ）=-1θ2-θ1（g1（x1;θ），g2（x1，x2;θ），…，gn（x1，x2，…，xn;θ））′，

Jg=1θ2-θ1×11-α… （1-α）n-2（1-α）n-1

0α…α（1-α）n-3α（1-α）n-2

00… αα（1-α）

00… 0αn×n

当α=1时，Jg为单位矩阵，可以相应地得到休哈特控制图的单样本无偏梯度估计量。

3.2 质量特性值由均匀分布驱动的广义似然比估计量

均匀分布随机数可以产生服从任意分布的随机数，考虑由均匀分布驱动的质量特性值具有更广泛的应用场景。假设质量特性值Xi处于稳定的受控状态时的累积分布函数为F1（·）;质量特性值Xi处于不稳定的失控状态时的累积分布函数为F2（·）。仿真输出的质量特性值由独立同分布的服从均匀分布U（0，1）的随机变量构成的向量U（n）=（U1，U2，…，Un）驱动。（1）式中的N可以改写为：N=min{i：Yi[θ1，θ2]}=min{i：Zi[0，1]}，其中Zi=（Yi-θ1）/（θ2-θ1），i1。{Yi，i1}是一条马尔科夫链，则{Zi，i1}也是一条马尔可夫链：Z1=h1（U1;θ），Zi=（Zi-1，hi（Ui;θ））。（1）式中：1（N=n）=（∏n-1i=11（0Zi1））×（1-1（0Zn1）），∏0i=11。記Jh=Th为h（h1（u;θ），…，hn（u;θ））′的雅克比矩阵。如果Jh是可逆矩阵且h二阶连续可微，采用广义似然比法得到

E[N]θ=∑∞n=1nE[1（N=n）]θ

=∑∞n=1n∑ni=1E[（∏n-1j=11（0Z+ij1））×（1-1（0Z+in1））×ri（1-;θ）]-

∑∞n=1n∑ni=1E[（∏n-1j=11（0Z-ij1））×（1-1（0Z-in1））×ri（0+;θ）]+

∑∞n=1nE[（∏n-1i=11（0Zi1））×

（1-1（0Zn1））×dn（U（n）;θ）]

其中{Z+ij，j1}和{Z-ij，j1}是分别由U（n）i（U1，…，

1-第i个元素，

…，Un）和U（n）i（U1，…，0-第i个元素，…，Un）通过{Zi，i1}相应生成的马尔可夫链。ri（u;θ）=（J-1h（u;θ）θh（u;θ））′ei，i=1，…，n。dn（u;θ）=∑ni=1ei′J-1h（u;θ）（uiJh（u;θ））J-1h（u;θ）θh（u;θ）-tr（J-1h（u;θ）θJh（u;θ））。qJh表示对矩阵Jh中与q有关的相应元素求导数，x-和x+分别为x的左极限和右极限。A67D4071-5767-49FE-868D-67CB7CFF2701

对任意函数h～（·），记h～（x-）limx→x-h～（x），h～（x+）limx→x+h～（x）。

结合文献[20]的随机化方法，令N′1为概率质量函数f～的离散随机变量，得到

E[N]/θ的单样本无偏梯度估计量为

Guniform1（θ）=N′×（SN′（U（N′））+DN′（U（N′）））/f～（N′）

E[（N-「τ/Δ）+]/θ的单样本无偏梯度估计量为

Guniform2（θ）=（N′-「τ/Δ）+×（SN′（U（N′））+

DN′（U（N′）））/f～（N′）

其中Dn（U（n））=（∏n-1i=11（0Zi1））×

（1-1（0Zn1））×dn（U（n）;θ）

Sn（U（n））=∑ni=1（∏n-1j=11（0Z+ij1））×

（1-1（0Z+in1））×ri（1-;θ）-

∑ni=1（∏n-1j=11（0Z-ij1））×

（1-1（0Z-in1））×ri（0+;θ）

例4 考虑例3中的控制图优化设计问题。当仿真输出的质量特性值Xi的分布由均匀分布驱动时，对于指数加权移动平均控制图，马尔可夫链{Zi，i1}可以表示为：Z0=0，Zi=（1-α）Zi-1+hi（Ui;θ），i1。其中hi（Ui;θ）=αθ2-θ1[1（i<τ/Δ）F-11（Ui）+1（iτ/Δ）×F-12（Ui）-θ1]。进而得到

ri（u;θ）=-1θ2-θ1[1（i<τ/Δ）F-11（ui）f1（F-11（ui））+1（iτ/Δ）F-12（ui）f2（F-12（ui））-θ1]

dn（u;θ）=1θ2-θ1∑ni=1[1（i<τ/Δ）F-11（ui）f1（F-11（ui））+

1（iτ/Δ）F-12（ui）f2（F-12（ui））+1]

当α=1时，Zi=hi（Ui;θ），i1，可以相应地得到休哈特控制图的梯度估计量。

4 基于随机近似方法的最优控制上界求解

本节通过随机近似方法求解控制图经济设计的最优控制上界，在消除梯度估计量与真实梯度之间的偏差的同时，达到极小化控制图的单位时间内的平均运行成本的目标。考虑逐步增加仿真样本量和随机化仿真样本量的两种随机近似方法，并讨论相应的理论性质。

4.1 逐步增加仿真样本数量

该方法在参数优化迭代时，使用逐步增加仿真样本数量的方法计算C^k（θ）。为了证明逐步增加仿真样本数量的随机近似方法的全局最优性，提出如下假设：①C（θ）是θ∈R的严格凹函数;②C^k（θ）的二阶矩一致有界，即：supk∈NE[supθ∈RC^2k（θ）]<∞;且C^k（θ）是渐近无偏的，即：limk→∞E[C^k（θ）]=C（θ）/θ+limk→∞ Γk（θ）=C（θ）/θ，其中Γk（θ）为残差项;③步长序列与偏差序列满足：∑∞k=1αk=∞，∑∞k=1α2k<∞，∑∞k=1αkβk<∞和βk=supθ∈R|Γk（θ）|。

定理1 如果条件①～③成立，则limk→∞θ（k）=θ*，a.s.，其中a.s.表示几乎处处。

证明 令Πk（θ（k）-θ*）2，则E[Πk+1|θ（k），…，θ（1）]=Πk+2αkζk+α2kE[C^2（θ（k））]=Πk+2αk（ζ+k+ζ-k）+α2kE[C^2（θ（k））|θ（k））]，其中ζk（C（θ）/（θ|θ=θ（k）+Γk（θ（k）））（θ（k）-θ*），ζ+k12（ζk+|ζk|），ζ-k12（ζk-|ζk|）。令{kt}是滿足ζ+kt≠0的子序列，则

|C（θ）θ|θ=θ（kt）<|Γkt（θ（kt））|

由条件①和③

limt→∞（θ（kt）-θ*）=0， limk→∞∑∞t=kαtζ+t=0

令ΠkΠk+2∑∞t=kαtζ+t+∑∞t=kα2tE[C^2（θ（t））|θ（k），…，θ（1）]0，{Πk}是正的上鞅，因为E[Πk+1|θ（k），…，θ（1）]=Πk+2αkζ-kΠk。由条件②和③

limk→∞∑∞t=kα2tE[C^2（θ（t））|θ（k），…，θ（1）]=0

根据鞅收敛定理[21]，存在随机变量Π，使得

limk→∞Πk=limk→∞Πk=Π， a.s.

注意到

E[Πk]=E[Π1]+2E[∑kt=1αtζt]+∑kt=1α2tE[C^2（θ（t））]

由条件①，对任意δ>0，存在ε>0，使得

sup|θ-θ*|>δ|C（θ）/θ|>ε

若Pr（Π=0）≠1，则

∑∞k=1αkζk=∑∞k=1αt（C（θ）/θ|θ=θ（k）+Γk（θ（k）））（θ（k）-θ*）=-∞以正的概率成立，这与E[Πk]0和∑∞k=1α2kE[C^2（θ（k））]<∞的结论矛盾。因此，Pr（Π=0）=1。综上所述，定理的结论成立。证毕。

4.2 随机化仿真样本数量

该方法在参数优化迭代时，使用随机化仿真样本数量的方法计算C^k（θ）。具体地，令C^k（θ）∑kt=1Δt（θ），其中Δt（θ）C^t（θ）-C^t-1（θ），C^00。定义C（θ）∑t=1Δt（θ）/Pr（t），其中是与{C^k（θ）}独立的离散随机变量。根据文献[20]的定理1，C（θ）是C（θ）/θ的无偏梯度估计量，该证明可由limk→∞ E[C^k（θ）]=C（θ）/θ，∑∞t=1E[|Δt（θ）|]<∞，和下述结论得到：如果∑∞t=1E[|C^t-1（θ）-C（θ）/θ|2]/Pr（t）<∞，则C（θ）∈L2，E[C（θ）]=C（θ）/θ，其中L2为平方可积的随机变量的希尔伯特空间。随机化仿真样本数量的方法可能会导致较大的方差[22]，因此需要推导样本数量的最优随机分布。C（θ）的方差可以表示为A67D4071-5767-49FE-868D-67CB7CFF2701

E[C2（θ）]=∑∞t=1vt（θ）/Pr（t）

其中vt（θ）E[|C^t-1（θ）-C（θ）/θ|2]-E[|C^t（θ）-C（θ）/θ|2]。令P（N）为支撑集N的分布族，考虑如下有约束的优化问题

infPr∈P（N）：E[]=T{∑∞t=1vt（θ）/Pr（t）}

（2）

优化问题（2）本质上是一个最优控制问题，该问题的最优解即为最优随机分布。

定理2 如果vt（θ）0，vt（θ）vt+1（θ），优化问题（2）的解为

Pr*（t）=1，1t

（T+1-t*）vt/2/∑∞t=t*vt，tt*

其中t*min{t∈N：T+1-t∑∞l=tvl/vt}。

证明 考虑如下离散时间的最优控制问题

inf{μ（t）∈（0，1）：t∈N}{∑∞t=1vt/μ（t）}

s.t. （t+1）-（t）=μ（t）， t∈N

（1）=0， limt→∞（t）=T（3）

建立汉密尔顿函数：H（（t），μ（t），y（t+1），t）vt/μ（t）+y（t+1）μ（t），其中（t）为状态变量，μ（t）为控制变量。对于t∈N，最优控制μ*（n）满足极大值原理，其中最优条件：μ*（t）=infμ∈[0，1）H（（t），μ（t），y（t+1），t），伴随方程：y（t+1）-y（t）=-Hz（（t），μ（t），y（t+1），t）=0。

根据伴随方程，存在v∈R，y*（t）=v，t∈N。对于t0，虽然控制变量μ*（t）=1满足最优条件，但不满足最优控制问题（3）中的约束。因此，v∈R+，且μ*（t）=1，0t

若v1v，则t*=1，limt→∞ *（t）=∑∞t=1vt/v=T，即v=（∑∞t=1vt）2/T2，μ*（t）=Tvt/∑∞l=0vl。

若v1>v，则t*>1，limt→∞ *（t）=t*-1+∑∞t=t*vt/v=T，即v=（∑∞t=t*vt/（T+1-t*））2。因此，t*=min{t∈N：T+1-t∑∞l=tvl/vt}。相似地，可以证明t*>1当且仅当v1>（∑∞l=1vl）2/T2。如果vt非负且非增，则最优控制μ*（t）非增，且limt→∞ μ*（t）=0。因此，Pr*（t）=μ*（t）。证毕。

5 数值实验

本节通过数值实验介绍本文提出的控制图经济设计方法在休哈特和指数加权移动平均控制图中的应用。为了方便进行数值实验，考虑常数的控制图界限，即：θ1，i=θ1，θ2，i=θ2。在给定控制图的控制下界θ1的条件下，优化设计控制图的控制上界θ=θ2。数值实验在搭载英特尔酷睿i5-11300H处理器的Windows系统计算机上通过Matlab R2021a软件进行测算。

5.1 质量特性值服从正态分布

假设质量特性值Xi处于稳定的受控状态时，服从均值为1，方差为1的正态分布;质量特性值Xi处于不稳定的失控状态时，服从均值为2，方差为4的正态分布。设定系统失控时间τ服从均值为20的指数分布，采样间隔时间Δ=1，控制图的控制下界θ1=-1。令损耗成本c=1，系统维修成本C=3。控制图的初始控制上界θ2=1。设定随机近似方法迭代步长αk=1/k。设定逐步增加仿真样本量的随机近似方法中，第k次迭代使用1000+k个仿真样本;随机化仿真样本量的随机近似方法中，第k次迭代使用的仿真样本数量服从成功概率为10-4的几何分布。对于休哈特控制图，两种随机近似方法分别迭代K=104和K=5×103次。对于不同参数设定的指数加权移动平均控制图：α=0.2，0.4，0.6，0.8，两种随机近似方法分别迭代K=2×103和K=103次。表1展示了两种随机近似方法迭代估計的最优参数值θ（K）和分别通过108次独立仿真实验估计的初始平均运行成本C（θ（0））和最优平均运行成本C（θ（K））。图1展示了对于α=0.2的指数加权移动平均控制图，两种随机近似方法迭代得到的样本轨道。

从表1中可以观察到，两种随机近似方法得到相近的最优控制上界的估计值。通过对控制图的控制上界进行优化设计，过程的平均运行成本有显著的下降。虽然逐步增加仿真样本量的随机近似方法消耗了更多的迭代次数，但随机化仿真样本量的随机近似方法在每步迭代时随机消耗均值为104个仿真样本，导致运算时间更长。例如，在不同参数设定的指数加权移动平均控制图中，虽然逐步增加仿真样本量的随机近似方法的迭代次数是随机化仿真样本量的随机近似方法的迭代次数的2倍，但后者的平均运算时间约为前者的3.5倍（前者：约638.47秒;后者：约2220.00秒）。

（a）逐步增加仿真样本量（b）随机化仿真样本量图1 α=0.2的指数加权移动平均控制图控制上界θ2的样本轨道

5.2 质量特性值由均匀分布驱动

假设质量特性值Xi处于稳定的受控状态时，服从[-1，1]区间上的均匀分布，即Xi=2Ui-1;质量特性值Xi处于不稳定的失控状态时，服从[1，2]区间上的均匀分布，即Xi=Ui+1。此时，F-11（Ui）=2Ui-1，F-12（Ui）=Ui+1。相应地，

ri（u;θ）=-1θ2-θ1[1（i<τ/Δ）（ui-12）+

1（iτ/Δ）（ui+1）-θ1]

dn（u;θ）=1θ2-θ1∑ni=1[1（i<τ/Δ）（4ui-2）+1（iτ/Δ）（ui+1）+1]

设定系统失控时间τ服从均值为5的指数分布，其余系统参数设置与5.1节的实验相同。随机化方法中的离散随机变量N′服从成功概率为0.1的几何分布。设定随机近似方法迭代步长αk=1/k。设定逐步增加仿真样本量的随机近似方法中，第k次迭代使用1000+k个仿真样本;随机化仿真样本量的随机近似方法中，第k次迭代使用的仿真样本数量服从成功概率为10-5的几何分布。对于休哈特控制图和不同参数设定的指数加权移动平均控制图：α=0.1，0.3，0.5，0.7，两种随机近似方法分别迭代K=5×104次和K=104次。表2展示了两种随机近似方法迭代估计的最优参数值和分别通过108次独立仿真实验估计的初始平均运行成本C（θ（0））和最优平均运行成本C（θ（K））。图2展示了对于休哈特控制图，两种随机近似方法迭代得到的样本轨道。A67D4071-5767-49FE-868D-67CB7CFF2701

從表2中可以观察到与表1相同的结论，即：两种随机近似方法得到相近的最优控制上界的估计值、过程的平均运行成本有显著的下降。随机化仿真样本量的随机近似方法在每步迭代时随机消耗均值为105个仿真样本，导致运算时间更长。在不同参数设定的指数加权移动平均控制图中，虽然逐步增加仿真样本量的随机近似方法的迭代次数是随机化仿真样本量的随机近似方法的迭代次数的5倍，但后者的平均运算时间约为前者的1.2倍（前者：约2.09×104秒;后者：约2.59×104秒）。

6 结论与启示

本文基于随机梯度估计方法提出一种控制图的经济设计方法。管理者期望在制造生产流程运作的同时实现控制图界限优化的经济设计目标。控制图的经济性评价指标同时考虑系统失控后的损耗成本和系统判定失控后的维修成本。由于控制图边界属于结构参数且关于控制图的系统表现不连续，本文采用随机梯度估计方法中的广义似然比法估计控制图的经济性评价指标关于控制图界限的梯度。结合逐步增加仿真样本量和随机化仿真样本量的随机近似方法优化控制图界限，并讨论了随机近似方法的理论性质。特别地，本文考虑对控制图控制上界的优化，给出了当质量特性值服从正态分布和其分布由均匀分布驱动时的梯度估计量。在数值实验中，介绍了本文提出的控制图经济设计方法在休哈特控制图和指数加权移动平均控制图中的应用，表明了方法的有效性。研究成果为控制图的经济优化设计提供了一种新的求解思路。未来的研究可以考虑更多影响系统运行成本的因素。采用强化学习方法对控制图进行经济优化设计也是可以进一步研究的方向。

参 考 文 献：

[1]Shewhart W A. Economic control of quality of manufactured product[M]. Macmillan And Co Ltd， London， 1931.

[2]Hsieh K L， Tong L I， Wang M C. The application of control chart for defects and defect clustering in IC manufacturing based on fuzzy theory[J]. Expert Systems with Applications， 2007， 32（3）： 765-776.

[3]Sego L H. Applications of control charts in medicine and epidemiology[M]. Virginia： Virginia Polytechnic Institute and State University， 2006.

[4]Stewart B， James R， Knowlton K， et al.. An example of application of process control charts to feed management on dairy farms[J]. The Professional Animal Scientist， 2011， 27（6）： 571-573.

[5]程宏波，王佳鑫，刘杰，等.基于改进多元统计控制图的接触网状态综合评价方法[J].铁道科学与工程学报，2021，18（11）：3048-3056.

[6]Westgard J O， Barry P L， Hunt M R， et al.. A multi-rule shewhart chart for quality control in clinical chemistry[J]. Clin Chem， 1981， 27（3）： 493-501.

[7]Huang W， Shu L， Jiang W. A gradient approach to efficient design and analysis of multivariate EWMA control charts[J]. Journal of Statistical Computation and Simulation， 2018， 88（14）： 2707-2725.

[8]Lorenzen T J， Vance L C. The economic design of control charts： a unified approach[J]. Technometrics， 1986， 28（1）： 3-10.

[9]Bai D S， Lee K T. An economic design of variable sampling interval X control charts[J]. International Journal of Production Economics， 1998， 54（1）： 57-64.

[10]Chen Y K. Economic design of X control charts for non-normal data using variable sampling policy[J]. International Journal of Production Economics， 2004， 92（1）： 61-74.

[11]Naderkhani F， Makis V. Economic design of multivariate Bayesian control chart with two sampling intervals[J]. International Journal of Production Economics， 2016， 174： 29-42.

[12]Ho Y C， Cao X R. Perturbation analysis of discrete-event dynamic systems[M]. Boston： Kluwer Academic Publisher， 1991.A67D4071-5767-49FE-868D-67CB7CFF2701

[13]Rubinstein R Y. The score function approach for sensitivity analysis of computer simulation models[J]. Mathematics and Computers in Simulation， 1986， 28（5）： 351-379.

[14]Pflug G C. Sampling derivatives of probabilities[J]. Computing， 1989， 42（4）： 315-328.

[15]Peng Y J， Fu M C， Hu J Q， et al.. A new unbiased stochastic derivative estimator for discontinuous sample performances with structural parameters[J]. Operations Research， 2018， 66（2）： 487-499.

[16]Peng Y J， Fu M C， Hu J Q， et al.. Generalized likelihood ratio method for stochastic models with uniform random numbers as inputs[J/OL]. Submitted to Operations Research. Preprint in https：//hal.inria.fr/hal02652068/document， 2020.

[17]Lele S. Steady state analysis of three process monitoring procedures in quality control[D]. Michigan： University of Michigan， 1996.

[18]Fu M C， Hu J Q. Efficient design and sensitivity analysis of control charts using monte carlo simulation[J]. Management Science， 1999， 45（3）： 395-413.

[19]Fu M C， Lele S， Vossen T W. Conditional monte carlo gradient estimation in economic design of control limits[J]. Production and Operations Management， 2009， 18（1）： 60-77.

[20]Rhee C H， Glynn P W. Unbiased estimation with square root convergence for SDE models[J]. Operations Research， 2015， 63（5）： 1026-1043.

[21]Karatzas I， Shreve S. Brownian motion and stochastic calculus[M]. Germaoy： Springer Science & Business Media， 2012.

[22]Cui Z， Fu M C， Peng Y， et al.. Optimal unbiased estimation for expected cumulative discounted cost[J]. European Journal of Operational Research， 2020， 286（2）： 604-618.A67D4071-5767-49FE-868D-67CB7CFF2701