堆载作用下高铁桥梁轨道形位变化的可靠度研究

宋旭明，王天良，唐冕，许珈豪

(中南大学土木工程学院，湖南长沙，410075)

既有高铁桥梁附近的大范围堆载会对桥梁的主体结构产生扰动。在我国长江三角洲、珠江三角洲、渤海湾等地区，软土欠固结、含水量高、强度低、压缩性大、沉降量大，堆载对既有桥梁结构会带来更大的安全隐患，甚至会改变桩体的设计控制状态。因此，合理地考虑软土区的土壤工程特性，综合桥梁下部结构等各方面的影响，讨论该地区桥梁在堆载条件下的安全可靠度，对于工程具有重大的参考意义。

目前，大量学者就堆载对临近结构物桩基的影响进行了研究。李志伟[1]通过实测发现单侧堆载作用下桩基将产生侧向偏移及附加弯矩，反弯点出现在2 种不同土层的交界处。竺明星等[2]根据Boussinesq 改进公式推导堆载产生的水平附加压力，采用Laplace 正逆变换求解桩身微分方程，应用矩阵传递法求得完整桩身响应量。黄挺等[3]通过边载及围载作用下的单桩室内模型试验研究了土表堆载分布形式对桩基负摩阻力作用的影响，发现土表堆载分布形式对桩基附加沉降具有明显影响。丁任盛[4]开展了堆载对临近桩基内力与变形影响的原位现场试验，探讨了深厚软土地区堆载高度、堆载与桩基距离等因素对桩身内力、位移、桩基和堆载间土体深层位移的影响规律。韩东亚等[5]用拉格朗日差分法分析了堆载和桩顶荷载组合作用下桩侧摩阻力分布、中性点位置变化规律，提出了快速估算中性点位置的方程式。聂如松等[6]基于实测数据，根据路基填筑前后桩基的应力变化求得了相应桩基弯矩，发现了对桩顶弯矩影响较大的因素为桩顶的约束情况。马学宁等[7]对群桩进行了围载和单侧边载作用下的模型试验，发现边载比围载同一位置桩身轴力、负摩阻力均较小，中性点位置较高。赵伟封等[8]采用极限平衡法，得到保证地基稳定的最大堆载高度以及带状堆载主要影响区的计算公式，判断带状堆载邻近桩基础是否受堆载影响，并得到带状堆载作用下地基土体侧移变形的计算深度及对邻近桩基础的推力计算公式。杨涛等[9]采用两阶段分析法分析了基坑开挖卸荷与堆载作用下邻近桩基的受力变形规律，发现了堆载对桩体水平位移的影响略大于堆载区域尺寸对桩体水平位移的影响。贺志勇等[10]用ABAQUS 软件建立了桥梁-地基土-堆载土模型，发现降低堆土高度和增大堆载间距均能有效控制地基土变形，降低桥梁结构的位移，堆土宽度对地基土侧向位移影响显著，对沉降影响较小。

目前的研究和试验为桥梁结构在堆载作用下的结构响应预测提供了理论基础和经验数据，但大多数研究未将桥梁的上部结构和轨道考虑在内。此外，土层力学参数离散性较大，计算结果的可靠性往往难以评估。为进一步研究堆载作用下高铁桥梁轨道的附加变形，本文作者采用单因素敏感性计算方法分析单侧堆载对于高铁轨道形位的各因素影响情况，确定参数的敏感性；通过Box-Behnken设计法进行试验设计，用二次回归正交设计得到与有限元模型相吻合的响应面模型；通过对响应面模型特征进行分析，确定各参变量对轨道形位的交互影响规律；使用Bootstrap 法对样本进行扩大并统计出拟建堆土区域的土层信息分布规律，对显著影响轨道形位的参数进行大量随机抽样，利用蒙特卡罗方法得到既有高铁轨道形位变化的可靠度，可为工程建设提供指导性建议，并为类似工程的轨道形位快速预测提供参考。

1 轨道形位变化的可靠度计算方法

1.1 参数敏感性分析

敏感性分析将各个要素对系统的影响程度进行分析，得出主要影响因素和次要影响因素，从而忽略次要影响因素[11]，在对计算精度和可靠度影响不大的情况下，可去除大量数据，降低计算的复杂程度。

采用扰动分析法计算参数敏感性。具体做法为选取1组待分析的要素，采用控制变量法，每次只变动1个要素值，然后将各参数代入有限元中进行分析，记录系统的扰动。具体步骤为：

1)选择与系统相关的影响参数，并确定参数的初值和扰动范围；

2)选定系统控制目标，分析各要素的变化对于系统影响程度；

3)对各要素进行量纲一化处理，定量分析各要素敏感度，并进行排序。

敏感度函数Si(xi)为系统控制目标扰动程度与要素变化程度的比值：

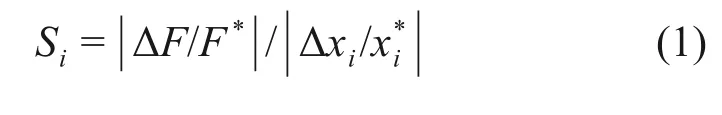
式中，Δxi为设计变量的摄动量；ΔF为系统特征值的变化量；xi*为设计变量的基准值；F*为系统特征值的基准值。

Si越大，基准状态下系统特征值F对xi越敏感。通过对比Si即可得出各要素的敏感度[12]。

1.2 响应面函数

响应面法是一种基于统计学与实验技术用来解决复杂系统输入与输出之间关系的数学方法。与有限元模型拟合较好的响应面模型可以在输入相同参数的情况下得到与有限元相同的计算结果，而计算效率更高，也被称为“有限元模型的模型”。在分析工程结构、系统内部受到大量非线性变量的影响时，可以利用多元回归来直观地表示多个变量与系统响应值之间的关系。

响应面法步骤为：首先对设计参数进行样本选取，然后进行统计回归分析，得到拟合的响应面并进行模型统计特征分析，计算拟合精度。常用的实验设计方法有全因子实验设计法、中心复合设计法(CCD)、Box-Behnken 设计法(BBD)等。BBD 设计法可以评价各因素与响应值之间的非线性关系，无需进行连续的多次实验，在因素数相同的情况下，试验组合较少，较为经济。

常用的响应面回归设计方法为二次回归正交设计，其优势在于所得的回归系数的估计之间相互独立，当后期出现一些问题需要删除某些因子时，不会影响其他回归系数的估计，从而易得出所有显著系数的回归方程[13]。三次方程和四次方程高度依赖试验样本的数量，当样本数量不足时，响应面极易出现扭曲，因此，仅在二次方程拟合结果不显著时使用。

通过参数敏感性分析得到敏感参数后，根据三水平值的BBD 设计法进行试验，采用二次回归正交设计法拟合得到二次多项式响应面模型。模型表达式如下：

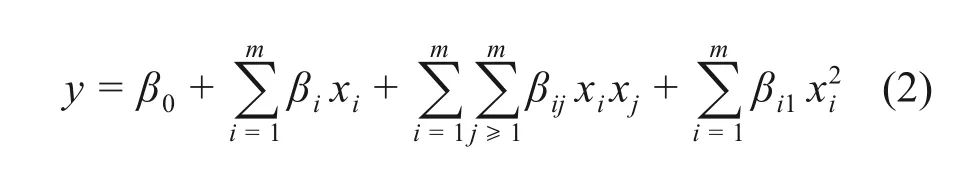
式中，β为待定系数，xi为影响参数。

1.3 可靠度计算理论

目前，工程结构中进行可靠度分析的方法主要有一次二阶矩法、二次二阶矩法、响应面法、蒙特卡罗抽样方法等。

蒙特卡罗法是随着计算机发展而逐步得到广泛使用的数值方法，其原理基于概率论大数定理中的Bernoulli 定理[14]。设结构的功能函数为Z=gX(X)，随机变量X的联合概率密度函数为fX(x)。按联合概率密度函数对随机变量进行抽样，用抽样所得样本代入结构功能函数中，若使Z＜0 成立，则记结构失效1次。当进行N次模拟时，假设Z＜0 出现了nf次。根据Bernoulli 定理，当N充分大时，随机事件Z＜0 在N次独立重复实验中的频率nf/N收敛于该事件的概率pf，因此，可得结构失效概率pf的估计值为nf/N。则结构的失效概率pf为

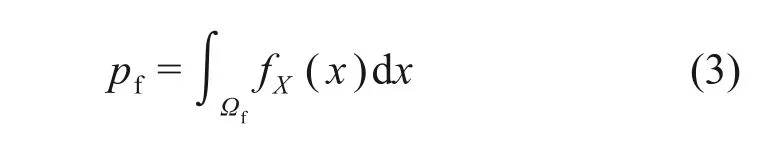
式中，Ωf为失效域。

对于大样本，根据中心极限定理，样本的均值Xˉ将渐进服从正态分布。为减小蒙特卡罗模拟的误差，常常增加模拟的次数即样本容量N；也可以采用方差缩减技术。当给定显著性水平α，进而已知标准正态分布的上分位值μα/2时(如α=5%，μ0.025=1.960 0)，可用代替pf，以此来估计给定模拟次数的误差，或根据误差来估计需要的模拟次数。对于实际工程结构，当误差精度在10-3～10-5数量级时，若相对误差小于20%的置信度为95%，则通常需要的模拟次数为105～107次。

本文采用高精度的蒙特卡罗方法对轨道形位可靠度进行分析，借助Matlab 平台完成参变量的随机抽样和形位幅值失效概率计算。具体分析步骤如下：

1)建立结构功能函数，可定义为Z=g(mi)，其中，mi是已知概率分布的随机变量。

2)对参变量进行随机抽样，产生1组随机变量mi，将其代入结构功能函数，求得此时的结构功能函数值。

3)重复N次步骤2)，统计N个功能函数值中超过可靠指标的个数。

4)根据大数定理，得到失效概率。

为满足蒙特卡罗的大样本要求，采用Bootstrap 法解决土层力学参数的小样本问题。Bootstrap 法也叫自助法，通过对小样本有放回地随机抽样，从而扩大了小样本数量，而且该方法在使用前无需知道原样本的分布规律，假设条件少，因此被广泛使用。其核心思路是运用再抽样技术代替理论分析，以足够多的实验观测数据统计特征代替真实母体的统计特征。具体方法是：首先从来自母体Pn的样本Xn中抽取M个容量为n的子样本其中依次计算M个子样本的方差，将这M个方差作为母体方差的观测值，从而得到新的自助分布，同时以该自助分布的方差作为母体方差的估计值，得到母体的离散情况。具体计算步骤为：

1)从原始样本中有放回地进行抽样，得到新的自助抽样样本，从而得到原始样本的经验分布。

2)计算待求参数的估计值，根据实际情况，待求参数可以是均值、方差、中位数等。

3) 重复步骤1)和2)M次，M通常为1 000 次以上。

只要M足够大，由M个估计值计算得出的分布特征参数即为母体对应参数的合理估计。

计算流程如图1所示。

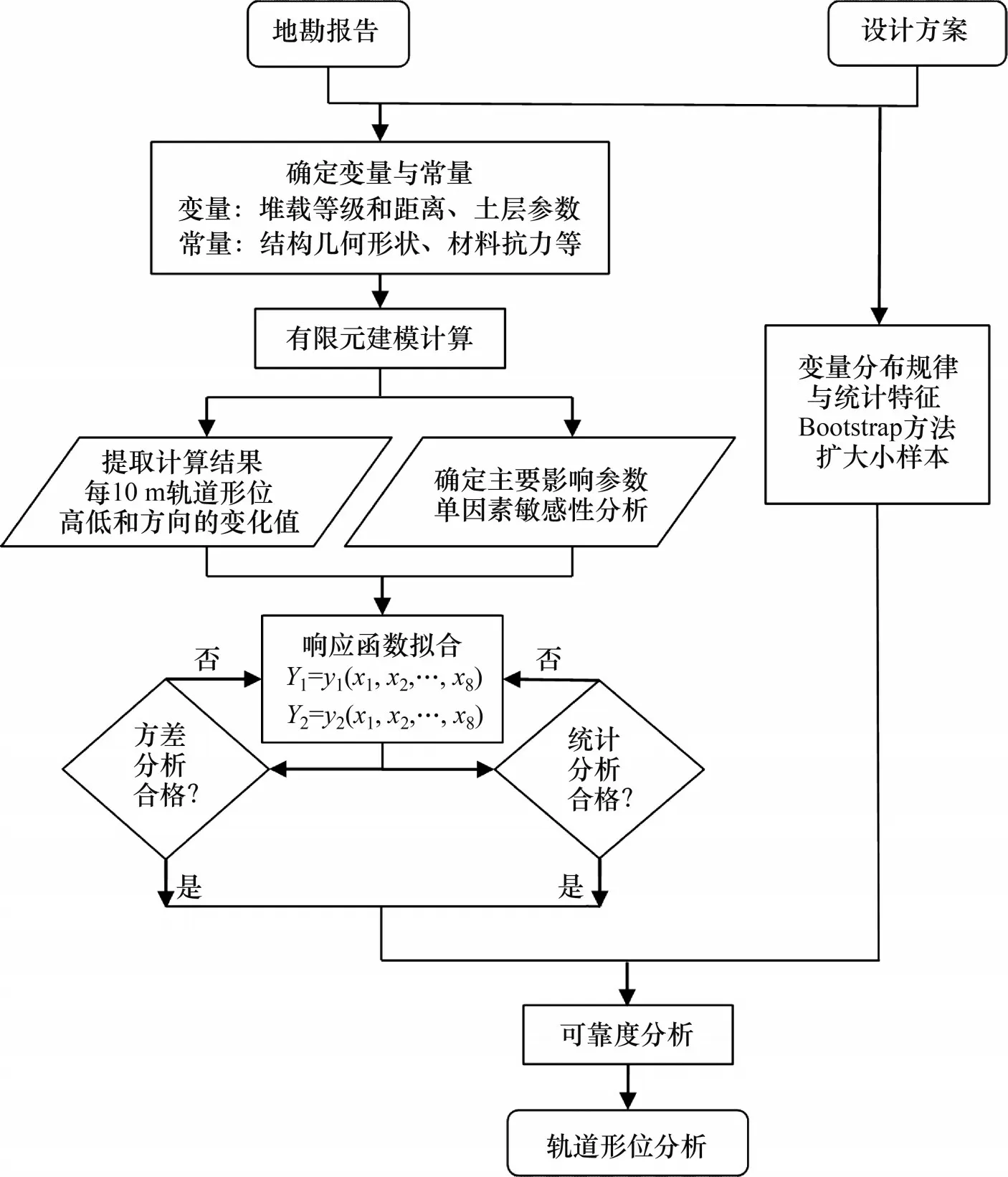
图1 可靠度计算流程图Fig.1 Flow chart of reliability calculation

2 轨道形位变化的敏感性分析

2.1 工程背景

福州地区沿合福(合肥—福州)高速铁路某工点附近规划有堆土造景工程，该工点处于华南地层区，地层分区性明显，上覆大面积第四系冲海积淤泥软土。高铁桥梁形式为跨度32 m 无砟轨道标准简支梁，设计时速300 km/h，圆端型桥墩，钻孔灌注桩，如图2 所示。在距离铁路15 m 的位置规划修建1 条长75 m，宽40 m 的景观带，堆载等级80 kPa。堆载区域与合福高铁相对位置关系如图3所示。

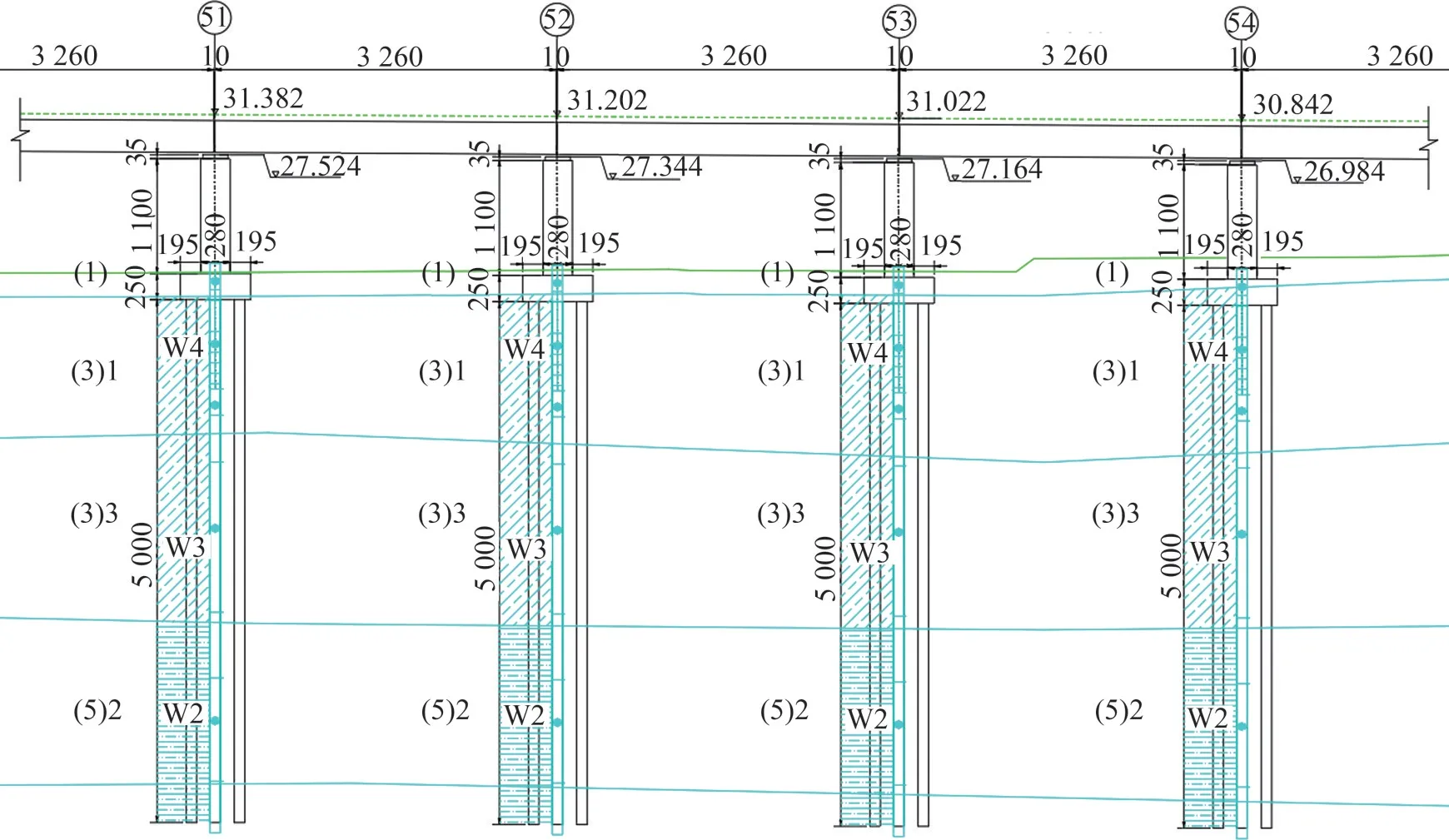
图2 铁路桥梁布置Fig.2 Railway bridge layout

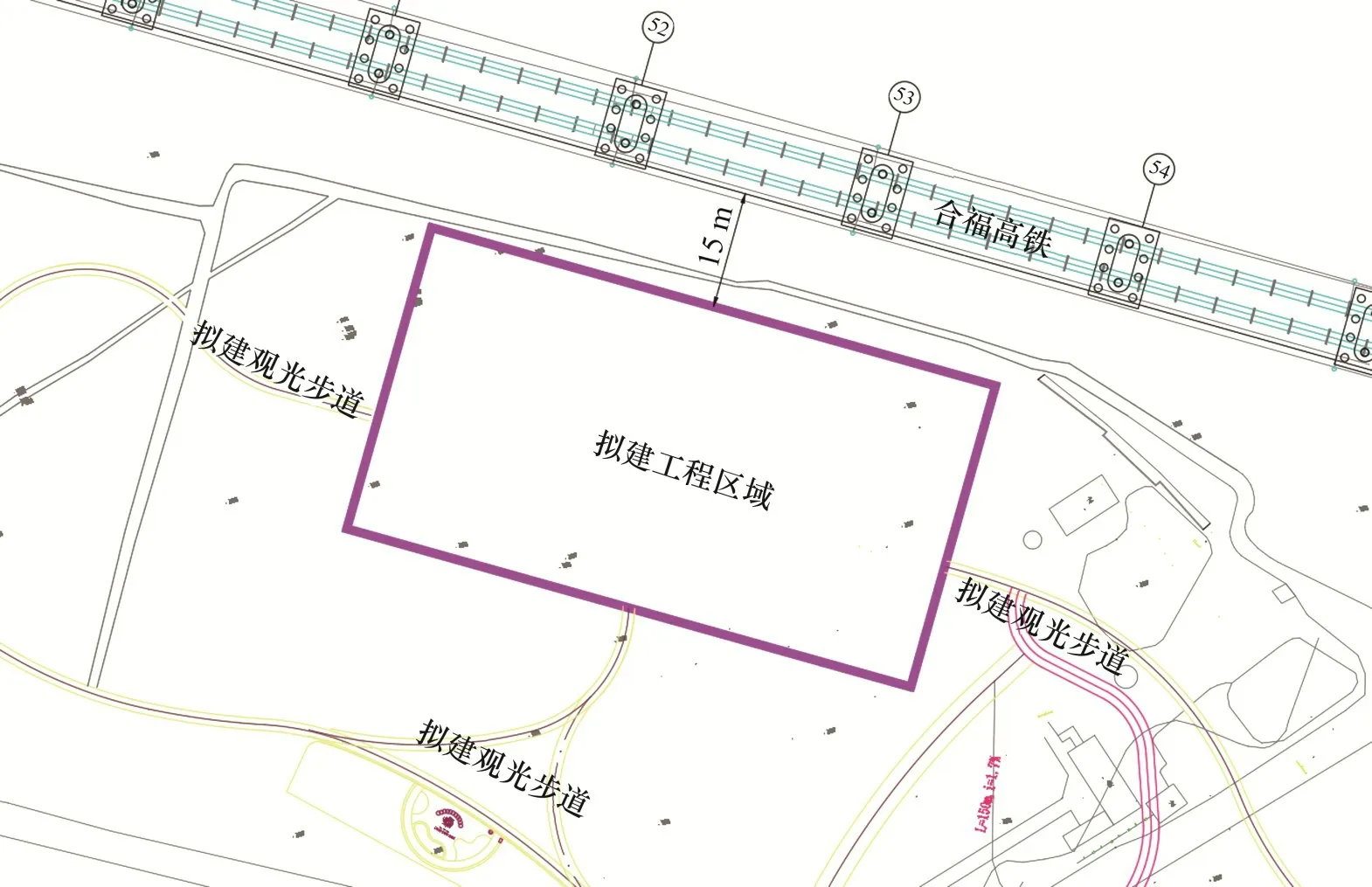
图3 工点平面Fig.3 Construction site plane

考虑到既有高铁列车运行安全性，需合理评估堆载方案对轨道形位变化的影响。根据方案建议，堆土距离可调整的范围为5～25 m，堆土荷载等级的调整范围为40～120 kPa。

在工点区域内，土层自上而下依次为：1)杂填土，厚度为2.20 m；2)淤泥质土，厚度为14.15 m；3)残积砂质黏性土，厚度为15.65 m；4)强风化花岗岩，厚度为17.00 m；5)中风化花岗岩，层顶埋深约为49.00 m。

2.2 计算模型及参数

采用ABAQUS 建立铁路简支梁桥的三维有限元模型，土体沿X和Y方向均为200 m，厚度为120 m，采用摩尔-库仑本构模型。墩高为11 m，桩基梅花形布置，桩径为1 m，桩长为50 m。承台和桩基采用C30混凝土，墩身采用C40混凝土，箱梁为C50 混凝土，轨道为60 型标准钢轨。线路一侧长为75 m、宽为40 m 的区域用来模拟景观堆土荷载。土体及下部结构采用C3D8I 非协调单元，梁体和轨道采用B32 单元[15]。模型共112 712 个单元，146 587 个节点。模型的边界条件为顶面为自由面，两侧水平约束，底面取竖向和水平向约束。桥墩和梁体的之间采用耦合接触，梁与钢轨之间采用弹簧接触。采用非线性弹簧单元模拟扣件阻力，扣件竖向刚度取60 MN/m[16]，扣件横向阻力取135 MN/m[17]，扣件纵向阻力取值参考规范[18]。桩土之间，法向使用“硬接触”，切向采用“罚摩擦”，摩擦因数为0.38。建立的有限元模型如图4所示。

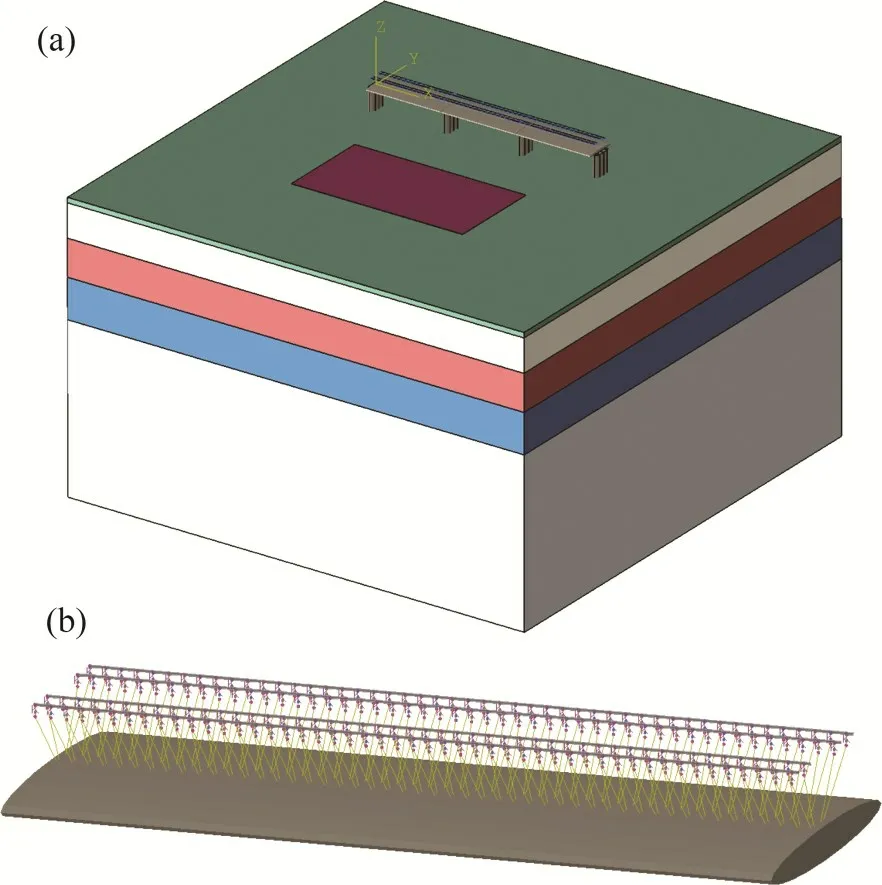
图4 有限元计算模型Fig.4 Finite element calculation model

2.3 轨道形位不平顺的参数敏感性分析

选取堆载等级、堆载距离以及淤泥层土、残积砂质黏性土、花岗岩的弹性模量、黏聚力、内摩擦角为变化参数，采用控制变量法，在保持其他参数不变的情况下，依次将各参数摄动1%，记录各参数摄动后轨道形位高低不平顺和方向不平顺幅值的变化，并据此计算每个参数的扰动幅度，从而分析既有高速铁路轨道形位的高低不平顺和方向不平顺幅值在各参数单独影响下的变化规律，得出各参数的影响程度。根据高铁地质勘察报告，认为土层参数服从正态分布，基准值取区间均值。各参变量取值区间及基准值如表1所示。

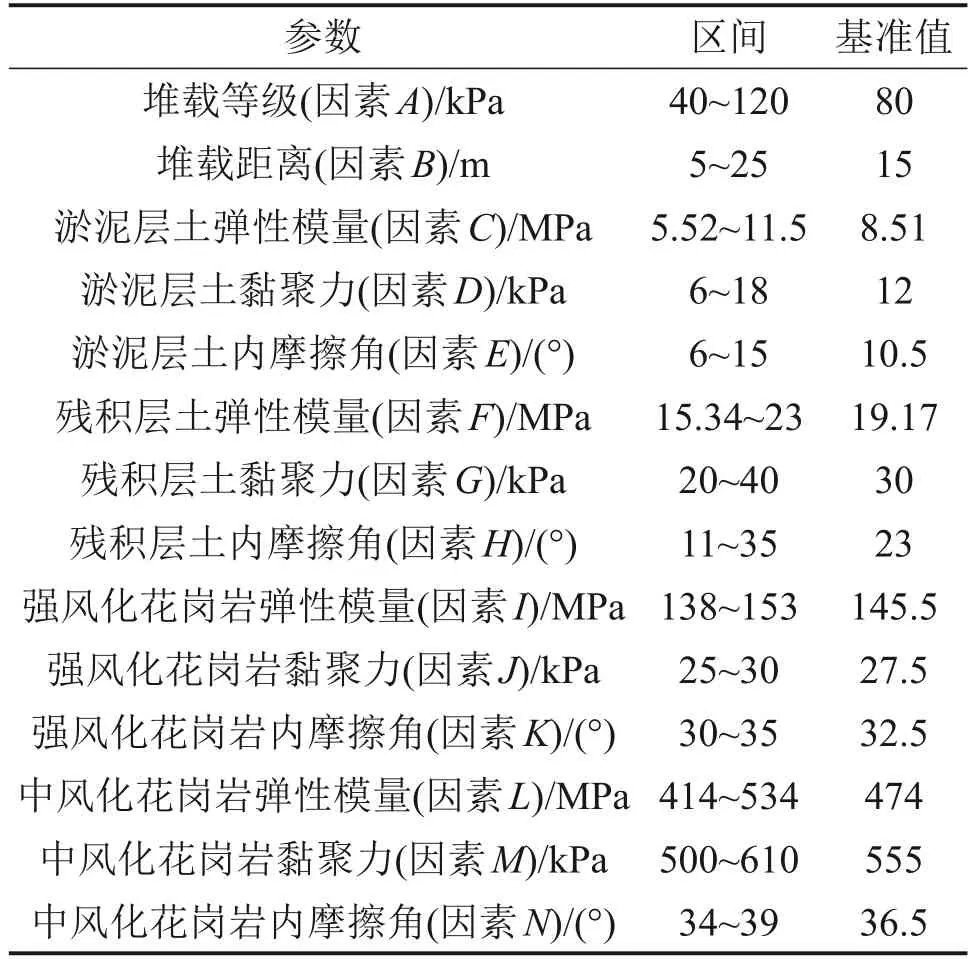
表1 模型参数集Table 1 Model parameter set

当各参数取基准值时，有限元计算得到的轨道形位中高低不平顺最大值为-0.921 3 mm，方向不平顺最大值为3.253 8 mm(弦长取10 m)。以此为基准，依次将各参数折减1%，提取轨道形位高低不平顺及方向不平顺计算结果，得到各参数的敏感系数如表2所示。

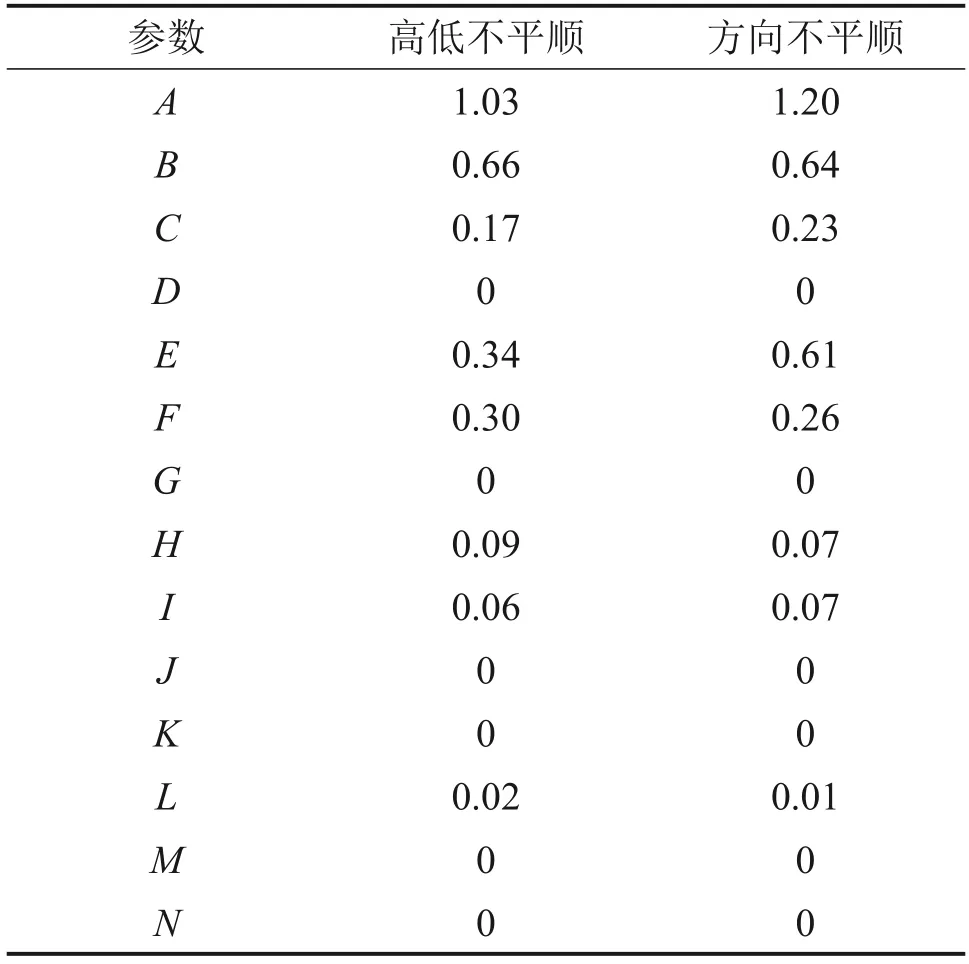
表2 轨道形位的参数敏感系数Table 2 Parameter sensitivity coefficient of track geometry

由表2 可得，堆载等级(因素A)对于形位的影响显著强于其他因素对形位的影响，堆载距离(因素B)次之，淤泥层土的内摩擦角(因素E)、残积层土弹性模量(因素F)、淤泥层土的弹性模量(因素C)在所有土体参数中影响最显著。而花岗岩的参数对轨道形位的影响基本可忽略不计。这说明对于堆载情况，下部持力层由于工程特性较好，其参数变化对上部建筑的影响不大，上部软弱土层的参数变化对结构的影响较为显著，应予以高度重视。因此，不考虑花岗岩土层的参数(因素I～N)离散性，将其作为常量拟合响应面。淤泥层土黏聚力(因素D)和残积土黏聚力(因素G)影响程度较同一土层的其他工程力学参数而言不显著，但考虑到在摄动较大的情况下，黏聚力会对响应面的拟合精度产生一定的非线性影响，为保证计算精度以及同一土层参数的完整，在响应面计算中将其作为参变量保留。

3 响应面函数拟合

将单因素敏感性分析结果中影响显著的主要影响因素作为变量，通过在整个参数的设计空间内构造合理的响应曲面，以显式的响应面模型逐步逼近设计参数与轨道形位变化幅值之间隐式的函数关系，得到简化的响应面模型来代替原有的有限元模型，可大大提高可靠度分析的计算效率。

3.1 函数模型拟合

因数A～H的三水平(0，-1，+1 分别代表该因素的平均水平、最低水平和最高水平)取值如表3所示。

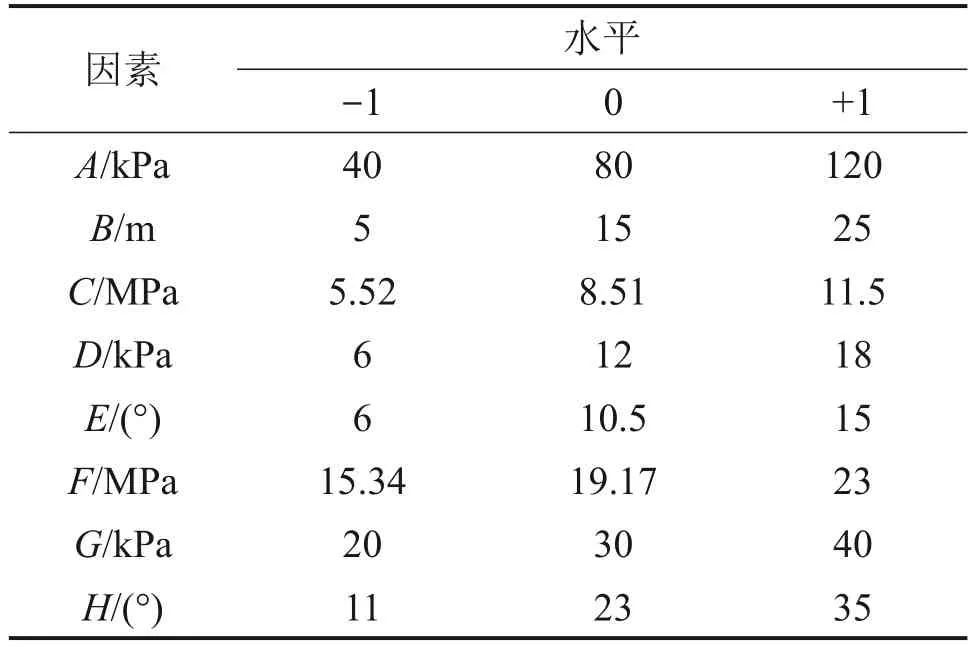
表3 响应面拟合Box-Behnken试验因素与水平Table 3 Response surface fitting Box-Behnken test factors and levels

根据每个因素的3个水平值，利用正交表构造实验方案，将8 个因素放入同一区组中，共进行113 组实验，其中包含1 个中心点(0，0，…，0)，112个因子点。

利用统计分析软件Design-Expert 10.0.4对有限元计算所得的113 组实验数据进行二次回归拟合，通过1个八元二次多项式确定轨道形位高低不平顺响应值(Y1)和轨道方向不平顺响应值(Y2)与参数A～H的相关性。模型系数由有限元计算结果的非线性回归获得，略去方程不显著项，得到的轨道形位变化的回归方程如下：

式中：各参变量前系数的绝对值表示该项因素对轨道形位变化的影响程度，正负表示影响方向。

可以看出，不论高低不平顺还是方向不平顺，各因素单独作用的影响程度均显著大于因素间的交互作用，说明堆载等级、堆载距离以及土体参数之间相关性弱，与真实情况相符，响应面模型的可靠程度较高。

3.2 模型统计特征分析

113组参数下响应面模型与有限元模型计算结果的相互关系如图5所示。

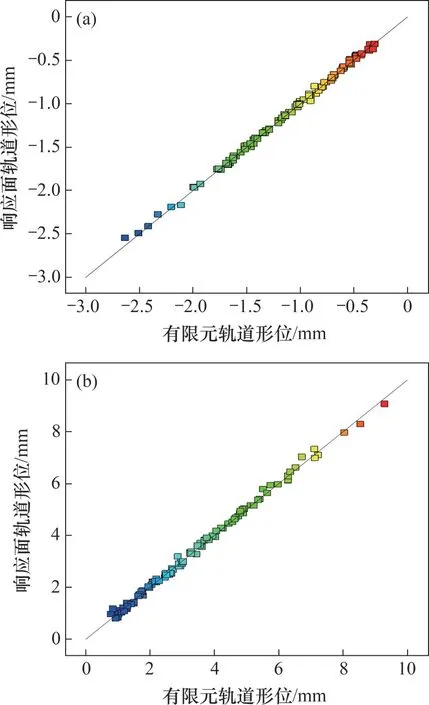
图5 响应面模型与有限元模型轨道形位计算值对应关系Fig.5 Corresponding relationship between of track geometry calculation values by response surface model and finite element model

由图5可知，全部因子点都接近斜率为1的直线，说明响应面模型与有限元模型之间吻合程度很高。高低不平顺模型的复合相关系数R2=0.998 0，校正复合相关系数方向不平顺模型的R2=0.995 8，均接近于1，说明各因素与响应面之间关联性好，该响应面的计算结果可以用来表征有限元计算结果。

3.3 响应面分析

三维响应面图可表示响应面中两因素交互作用的影响程度以及各因素的影响规律。图6所示为其他因素保持0水平值时，堆载等级与堆载距离交互作用影响轨道形位高低不平顺和方向不平顺的三维响应面图。

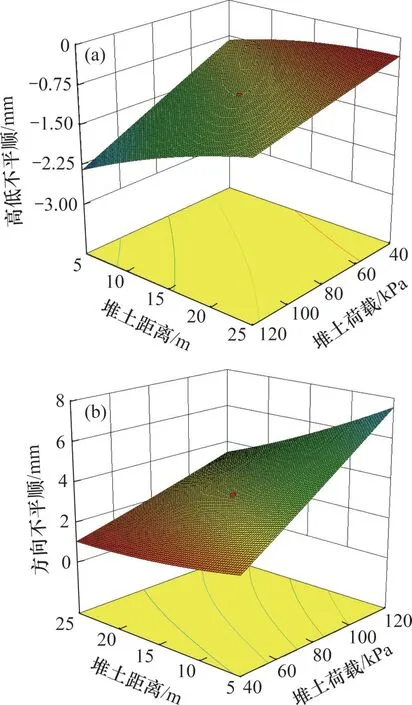
图6 堆载等级与距离交互作用对形位的影响Fig.6 Influence of interaction between surcharge grade and distance on shape and position

由图6可知，三维响应面在水平面投影出现了若干等高线，且等高线走向不平行于任意坐标轴，说明堆载等级和堆载距离对于轨道形位高低不平顺响应值均有很大的影响。等高线沿堆载等级坐标轴的斜率大于沿堆载距离的斜率，表示堆载等级对高低不平顺的影响要略大于堆载距离的影响，与轨道高低不平顺参数的敏感性分析结果一致。三维响应面图像整体从左下角至右上角呈上升趋势，高低不平顺响应值最小为-2.30 mm，最大为-0.34 mm。说明当堆载等级越小、堆载距离越远时，形位的高低不平顺幅值越小，与实际情况相符。方向不平顺的规律与高低不平顺的规律基本相似。

响应面中红色区域均代表形位变化小，也就是理想区域。由于2 种响应值的符号相反，因此，响应面中理想域的位置相反，且高低不平顺响应面图像上凸，而方向不平顺响应面图像下凹。

3.4 响应面预测精度验证

为进一步验证响应面的计算精度，根据表1中的参数变化范围由系统随机生成因素A～H的6组数据，响应面模型与有限元模型计算结果的比较如图7所示。

图7 响应面模型与有限元模型轨道形位计算值对比Fig.7 Comparison between response surface and finite element calculation of track geometry

由图7 可知，对于高低不平顺和方向不平顺，响应面与有限元的最大绝对误差分别为0.001 7 mm和-0.059 4 mm，最大相对误差分别为5.33%和7.53%。在实际工程中，当高速铁路轨道每10米弦长的形位幅度小于0.1 mm 时，对于列车运行的舒适性与安全性不会产生不利影响。因此，认为建立的响应面模型能较准确地反映有限元计算结果，可代替有限元模型对形位变化的可靠度进行分析。

4 轨道形位变化的可靠概率计算

4.1 基于Matlab的可靠度分析

将地勘报告中土层信息数据作为当地土层信息数据的随机样本，在Matlab中进行4 000次容量为300 的子样本抽样，并根据4 000 组样本的均值和标准差来计算母体的估计值。根据Bootstrap法，认为土层参数服从正态分布，其均值、标准差、变异系数见表4。

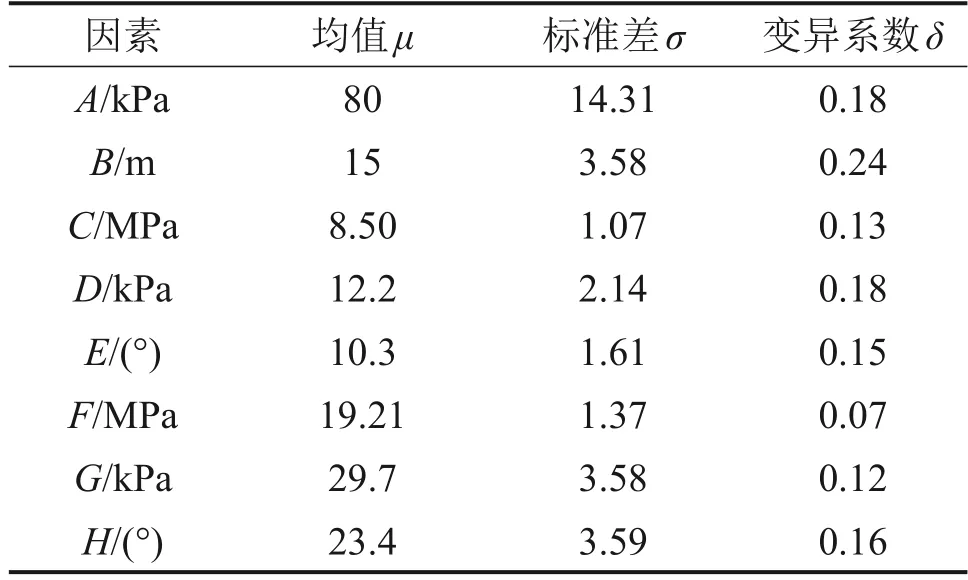
表4 随机变量分布参数Table 4 Random variable distribution parameters

高大钊等[19-20]的统计分析结果表明土体的主要力学参数服从正态分布或对数正态分布，与Bootstrap法模拟所得结果相吻合。

通过Bootstrap 法对样本扩容之后，采用蒙特卡罗法对高铁轨道形位的可靠度进行分析。以轨道形位的高低不平顺幅值和方向不平顺幅值为根据，建立轨道形位的计算功能函数。由于参数服从正态分布，可利用正态分布随机数发生器生成随机数。

在Matlab 中实现蒙特卡罗模拟的流程如图8所示。

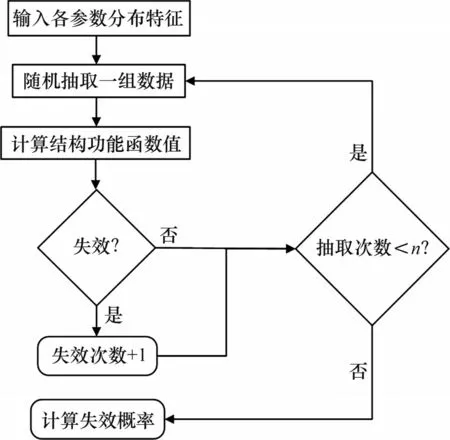
图8 蒙特卡罗模拟流程图Fig.8 Monte Carlo simulation flow chart

4.2 轨道形位概率计算

根据TB 10182—2017“公路与市政工程下穿高速铁路技术规程”[21]，目前高速铁路无砟轨道的高低不平顺和方向不平顺验收标准均是每10 米弦长的形位幅值小于2 mm。使用蒙特卡罗法计算轨道形位幅值小于1，2和3 mm且置信度为95%时的可靠概率，如表5所示。

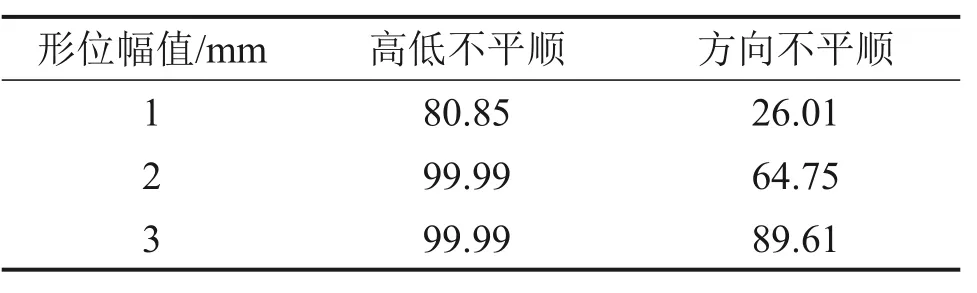
表5 各水平的可靠概率Table 5 Reliability probability of each level %

由表5可知，在置信度为95%时，高铁桥梁轨道形位高低不平顺幅值小于1 mm 的概率为80.85%，小于2 mm 和3 mm 的概率均为99.99%；轨道形位方向不平顺幅值小于1 mm 的概率为26.01%，小于2 mm 的概率为64.75%，小于3 mm的概率为89.61%。相比于高低不平顺，依托工程的方向不平顺可靠度偏低。

为了确保铁路安全运营，可减小堆土的荷载等级、增加堆载距离来提高铁路形位变化的可靠度。计算结果表明，当堆载减小到64 kPa，距离增加到18 m时，轨道形位高低不平顺小于2 mm的概率为99.99%，方向不平顺小于2 mm 的概率为95.60%，可以认为修改后方案的轨道形位变化不会对既有高铁的运营带来安全隐患。

5 结论

1)对于轨道形位高低不平顺，堆载等级和堆载距离敏感性系数分别为1.03和0.66，而对于轨道形位方向不平顺，两者分别为1.20和0.64，显著高于土层其他力学参数的敏感性系数。土层力学参数则呈现“短板效应”，即埋深越浅，工程特性越差的土层对轨道形位不平顺变化的影响越显著。

2)经过113次有限元计算得出了轨道形位高低不平顺和方向不平顺与堆载等级和堆载距离等8个主要影响参数的显式函数关系。响应面模型与有限元模型吻合程度很高，可以代替有限元模型进行可靠度分析。

3)使用Bootstrap 法在地质勘察资料有限的情况下统计出土层信息的分布特征，利用Matlab 平台，采用蒙特卡罗法将响应面函数作为结构功能函数进行可靠度分析，通过107次随机抽样计算，得出了依托工程方案在不同轨道形位变化幅值下的可靠概率，并给出满足可靠度要求的建议方案。

4)铁路轨道几何形位对列车运行的安全性、平稳性和舒适性意义重大，而高速铁路对轨道形位变化更为敏感，采用本文提出的方法可以方便地获得不同高铁轨道形位限值下计算结果的概率，也可为类似工程轨道形位变化的快速估算提供一条新途径，从而为高速铁路的安全评估提供参考。