典型压水堆小破口LOCA参数重要度排序表开发

熊青文，黄 涛，苟军利，杜 鹏，邓 坚，袁 鹏，周佳樾，胡文桢

(1.中国核动力研究设计院 核反应堆系统设计技术重点实验室，四川 成都 610213；2.西安交通大学 核科学与技术学院，陕西 西安 710049)

最佳估算加不确定性(BEPU)分析方法是国际原子能机构(IAEA)推荐用于核电厂安全分析和执照申请的先进方法[1]，该类方法的一般步骤为：首先基于确定的目标输出(FOM)建立现象识别排序表(PIRT)识别重要现象、模型或参数，并以带有真实不确定性分布的输入表示这些不确定性源；而后使用最佳估算程序建立电厂的模型，并执行多次程序计算将输入参数的不确定性传播至FOM；最后基于程序计算结果量化FOM的不确定性，并执行相应的不确定性分析和敏感性分析。由于核电厂的结构十分复杂，因此在模拟电厂时会涉及数量庞大的输入参数，如初始/边界条件、材料物性、状态参数、本构模型等[2]。在BEPU分析中考虑所有参数的不确定性是不现实的，因此需要基于一定的方法筛选和识别在分析工况中比较重要的参数以简化分析。其中，PIRT是最常使用的一种方法。通常而言，PIRT的建立需要使用一定的方法，如AHP[3]或MCDA[4]等，并在专家经验的指导下使用定性的方法表征现象或参数的重要度，如使用H、M和L分别表征高、中、低重要度[5]。PIRT能初步识别事故分析过程中的重要现象、模型或参数，但是在实际应用中会存在一些问题。首先，PIRT建立的成本很大。由于不同反应堆在不同工况下的事故序列和热工水力现象存在区别，因此理论上针对不同的反应堆堆型和不同的事故工况均要建立对应的PIRT，导致很多特定的反应堆不存在完善的PIRT，难以开展BEPU分析而使用保守参数进行保守分析。此外，PIRT的建立高度依赖于专家经验，在专家经验不足的情况下往往采取的措施是参考类似反应堆的已有PIRT，这种方式存在可能将不重要的参数考虑在内，而将重要参数遗漏的问题。

核电厂安全分析中失水事故是最为关注的工况之一，相比于大破口失水事故而言，小破口失水事故(SBLOCA)的BEPU分析研究较少，相关的PIRT也存在不多。为了能在缺乏PIRT的情况下执行准确的参数重要度排序计算，本文以典型三回路压水堆(PWR)不同破口尺寸下的SBLOCA为对象开展相关工作，选定的FOM为堆芯活性区最低坍塌液位(MCL)。首先，分别在冷管段横截面积的0.2%、0.4%、0.6%、0.8%和1.0%的5个破口尺寸下开展SBLOCA的瞬态基准计算，确定工况中的阶段划分，并确定堆芯MCL会出现于喷放和环路水封存在及清除阶段两个阶段。随后，使用优化矩独立全局敏感性分析方法对5个破口工况中两个阶段分别执行定量敏感性分析，并将参数的重要度排序转换为Savage分数，按照Savage分数将所有输入参数进行重要度分组，从而得到PWR SBLOCA的参数重要度排序表。

1 优化矩独立方法介绍

本文使用的敏感性分析方法为矩独立全局敏感性分析方法[6]，其旨在评估输入参数对目标输出概率密度函数(PDF)的影响，通过固定输入参数的取值并计算目标输出的无条件和条件PDF间的偏移量来定量评估参数的敏感性度量。假设某个模型Y=g(X)存在k个输入参数，第i个输入参数的矩独立敏感性度量δi可表示为：

(1)

(2)

式中：fXi(xi)为第i个输入参数的概率分布，xi为第i个输入参数Xi在计算中的取值；s(Xi)为固定第i个输入参数情况下输出PDF的偏移量；fY(y)、fY|Xi(y)分别为Y的无条件和条件PDF，y为输出参数Y在计算中的取值。

由于计算参数的矩独立敏感性定量涉及到两个嵌套积分计算，因此总体的计算量十分巨大。考虑到核电厂SBLOCA工况的模拟特别耗时，一次计算需耗费数小时，因此难以采用常规抽样方法直接计算各输入参数的矩独立敏感性度量。为了能使计算成本特别小且又可相对精确地计算输入参数的敏感性度量，本文使用一种优化的矩独立全局敏感性分析方法。首先，为了降低积分计算的计算量，使用五点高斯求积方案替代积分计算[7]。基于高斯求积方案，可将矩独立敏感性度量表示为：

(3)

式中：ωij为第i个输入参数按照其分布类型确定的5个高斯权重值中的第j个值；Xij为第i个输入参数的第j个高斯点取值。因此求解度量δi的关键在于求解s(Xij)，即输出的无条件PDF与将第i个输入参数固定于其第j个高斯点时输出条件PDF间的偏移量。

Liu等[8]提出了一种基于输出Y的条件和无条件累计分布函数(CDF)计算s(Xij)的方法，计算得到输出的CDF即可快速计算s(Xij)。根据CDF的定义可表示为：

FY(y)=P{Y≤y}=P{g(X)≤y}=

P{g(X)-y≤0}=P{z(X,y)≤0}=

Pf{z(X,y)}

(4)

式中：z(X,y)=g(X)-y为定义的新函数；Pf为失效概率。因此，可将求解模型Y=g(X)的CDF转换为求解模型z(X，y)的失效概率。优化方法中，使用四阶矩估计方法[9]和Pearson系统[10]来求解模型的失效概率。

由于采用五点高斯求积方案简化计算，因此每个参数仅需计算5个高斯点处对应的函数输出值，同时执行1次所有参数的名义值计算，因此该方法需要调用的模型计算次数最多为5k+1次。传统计算矩独立敏感性度量所需的计算次数常为输入参数数量的数万至数百万倍，相比于传统基于随机抽样的矩独立敏感性度量计算方法而言，本文提出的方法能够以极小的计算量达到类似的计算精度。使用失水事故试验(LOFT)中的LP-02-6工况对提出的方法进行验证[11]，验证计算中使用了15个重要输入参数，分别使用提出方法和传统抽样方法计算输入对包壳峰值温度的影响，其中抽样方法抽样计算次数为1.001×106，而优化方法总计算次数仅为81。两种方法的计算结果如图1所示，结果表明，在计算量缩小近1万倍的情况下，对于大部分输入参数该提出方法与传统方法计算结果的相对偏差在0.8%～5.2%内。

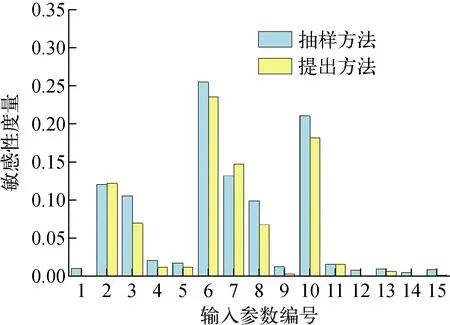
图1 LOFT LP-02-6工况敏感性分析结果

2 SBLOCA瞬态分析

本文考虑的工况为典型PWR 5个不同破口尺寸下的SBLOCA，首先执行所有参数取名义值的基准工况计算，并基于计算结果分析SBLOCA瞬态。计算结果表明，SBLOCA的事故进程可根据现象分为4个阶段，这4个阶段及其主要现象介绍如下。

1)喷放阶段

小破口出现后，冷却剂快速从破口处流失，导致一回路压力快速下降。但由于反应堆此时还未触发停堆状态，主泵还在持续运转，一回路的冷却剂处于受迫循环状态。当反应堆停堆后，保守假设主泵立即停止运行，主泵在惰转一段时间后停止，此时一回路内冷却剂进入自然循环阶段。

2)自然循环阶段

主泵停止转动后，一回路冷却剂处于自然循环阶段。此时堆内冷却剂依靠密度差进行流动，自然循环阶段持续时间往往较短。

3)环路水封存在及清除阶段

当一回路压力降至饱和压力时，一回路内冷却剂开始沸腾，产生大量蒸汽。由于破口尺寸较小，蒸汽不能及时从破口排出，导致积聚在上腔室和蒸汽发生器(SG)U型管内，蒸汽的积聚又阻碍了冷却剂的流动，进一步导致换热恶化，这个现象被称为环路水封。环路水封的出现会导致堆芯液位快速下降。随着一回路冷却剂从破口的不断流出，环路水封被逐渐清除，一回路压力恢复下降，且堆芯液位开始被安注系统恢复。

4)长期冷却阶段

环路水封清除后，堆芯液位开始恢复，直至完全淹没，过冷冷却剂能持续稳定地带走堆内的衰变热。

对于破口尺寸较小的SBLOCA工况(如0.2%破口工况)而言，其堆芯活性区MCL出现在喷放阶段，主要原因是闪蒸现象导致的堆芯局部沸腾及破口的冷却剂流出。而对于破口尺寸较大的SBLOCA工况而言，其堆芯活性区MCL出现在环路水封存在及清除阶段，主要原因是堆内传热恶化导致的堆芯强烈沸腾及破口的冷却剂流出。由于两种情况下堆芯活性区MCL出现的原理不同，后续敏感性分析应分为两个阶段独立开展，以评估各输入参数在喷放阶段和环路水封存在及清除阶段对堆芯活性区MCL的影响。

3 敏感性分析

由于缺乏PWR SBLOCA相关PIRT，因此拟参考类似研究中建立的PIRT或使用的重要参数，并结合目标电厂补充相关参数。诸多针对SBLOCA的PIRT中，西屋公司针对AP600开发的PIRT包含了典型能动式压水堆和非能动式压水堆中的主要现象，具有较高的可信度，因此本文主要参考的PIRT为AP600核电厂的SBLOCA PIRT[12]，但不包含非能动设备相关的现象或参数。此外，还参考了文献[13-15]中对SBLOCA工况开展BEPU分析时使用的重要参数。基于参考类似PIRT共识别了34个输入参数，此外，通过分析基准工况计算中出现的重要现象，补充了可能存在重要影响的模型或参数共20个输入，因此在敏感性分析计算中共考虑了54个输入参数。根据提出的优化矩独立全局敏感性分析方法，54个输入参数执行全局敏感性分析需进行217次程序计算。因此，使用所有54个不确定性输入参数执行全局敏感性分析，于5个破口尺寸工况各执行217次程序计算，并进一步计算54个输入参数在喷放阶段和环路水封存在及清除阶段对堆芯活性区MCL的矩独立敏感性度量。计算结果如图2所示，由于0.2%破口尺寸下没有环路水封存在及清除阶段，因此没有相应的敏感性分析结果。

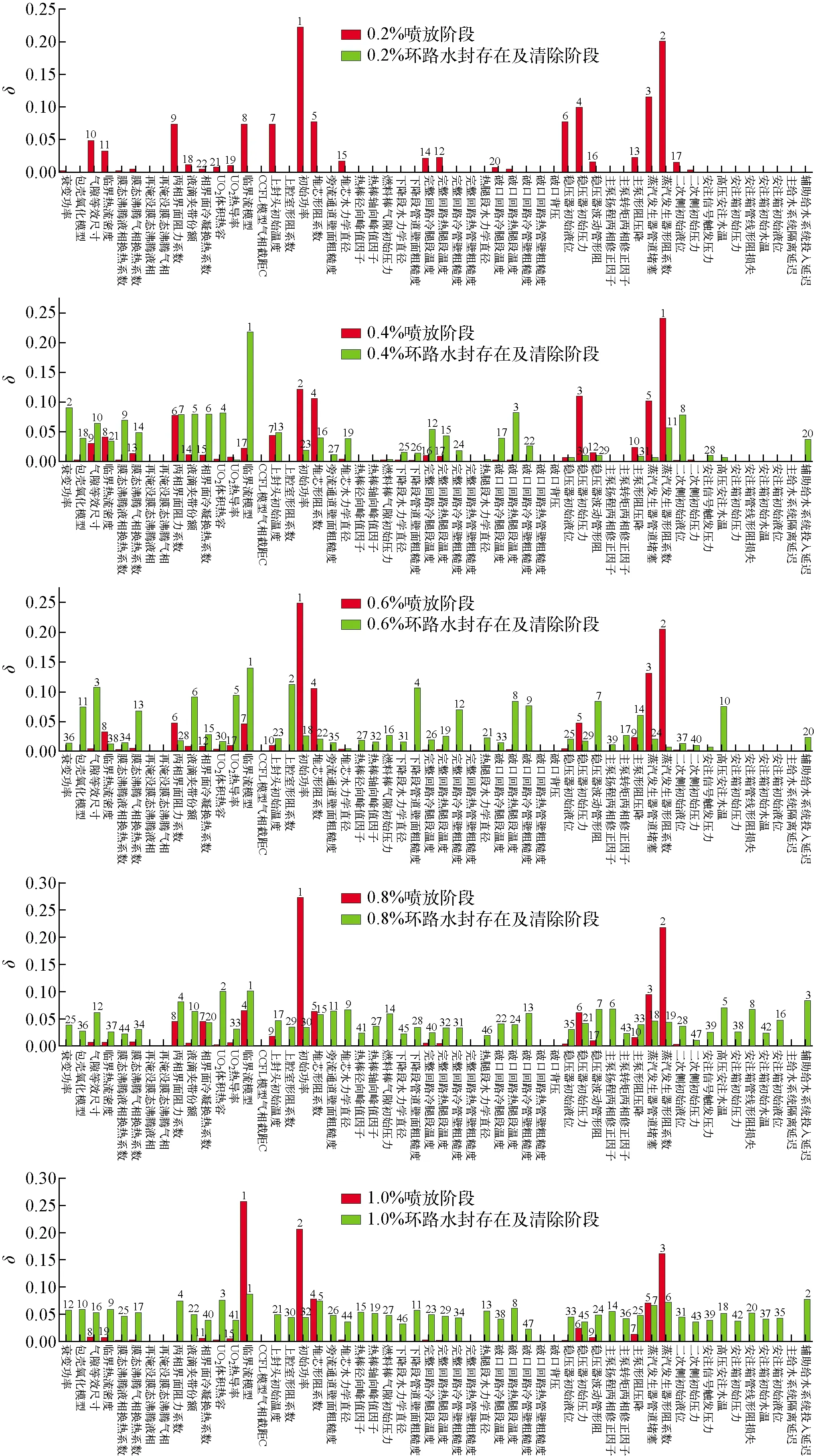
图2 0.2%、0.4%、0.6%、0.8%、1.0%破口尺寸工况敏感性分析结果

根据Pareto法则[16]，复杂模型可被小部分重要的参数和大部分影响较小的参数表征。图2示出了不同破口尺寸和不同事故阶段中各输入参数对堆芯活性区MCL的影响，表明大部分影响集中于少数重要输入参数，该结果符合Pareto法则。考虑到缺乏SBLOCA的PIRT，因此可基于敏感性分析结果建立参数重要度排序分组表，可为PWR SBLOCA工况BEPU分析提供参考和指导。需要说明的是，由于大部分影响集中于少数重要输入参数，若按照敏感性度量进行参数排序和重要度分组，会出现重要度排序为高的参数数量较少的情况。而且不同破口尺寸工况计算得到的各参数的敏感性度量无法直接比较，因此可将参数的重要度排序转换为Savage分数，然后将所有参数进行重要度定性均匀分组，分别为高(H)、中(M)、低(L)和无影响(N)。Savage分数的定义为：

(5)

式中：N为所有输入参数的数目；Ri为第i个输入参数的秩排序。

根据计算结果，喷放阶段有16个参数没有影响，其重要度排序为54，分组为N。剩余38个参数进行均匀分组，即排序1～13的参数分组为H，排序14～26的参数分组为M，排序27～38的参数分组为L。同理，在环路水封存在及清除阶段有7个参数对MCL没有影响，其分组为N，并对剩余47个参数进行均匀分组。根据最终对结果的处理，可得到PWR在SBLOCA工况下的参数重要度排序表(表1)。由表1可知，喷放阶段对MCL影响较大的参数主要为初始功率、初始一回路压力、临界流模型以及一回路中的流动阻力。而在环路水封存在及清除阶段，除破口冷却剂损失外，堆芯液位下降还与堆内沸腾有关，因此界面阻力模型、各种换热模型以及辅助给水系统延迟也对MCL有较大的影响。对比发现，提出方法计算得到的敏感性分析结果与参考PIRT较为相似，此外亦与现象机理具有高度一致性，因此可说明该敏感性分析结果的可信度。需要补充说明的是，该计算得到的PIRT能适用于典型能动式PWR SBLOCA工况的现象识别，亦可用作非能动式PWR SBLOCA工况的现象识别参考。

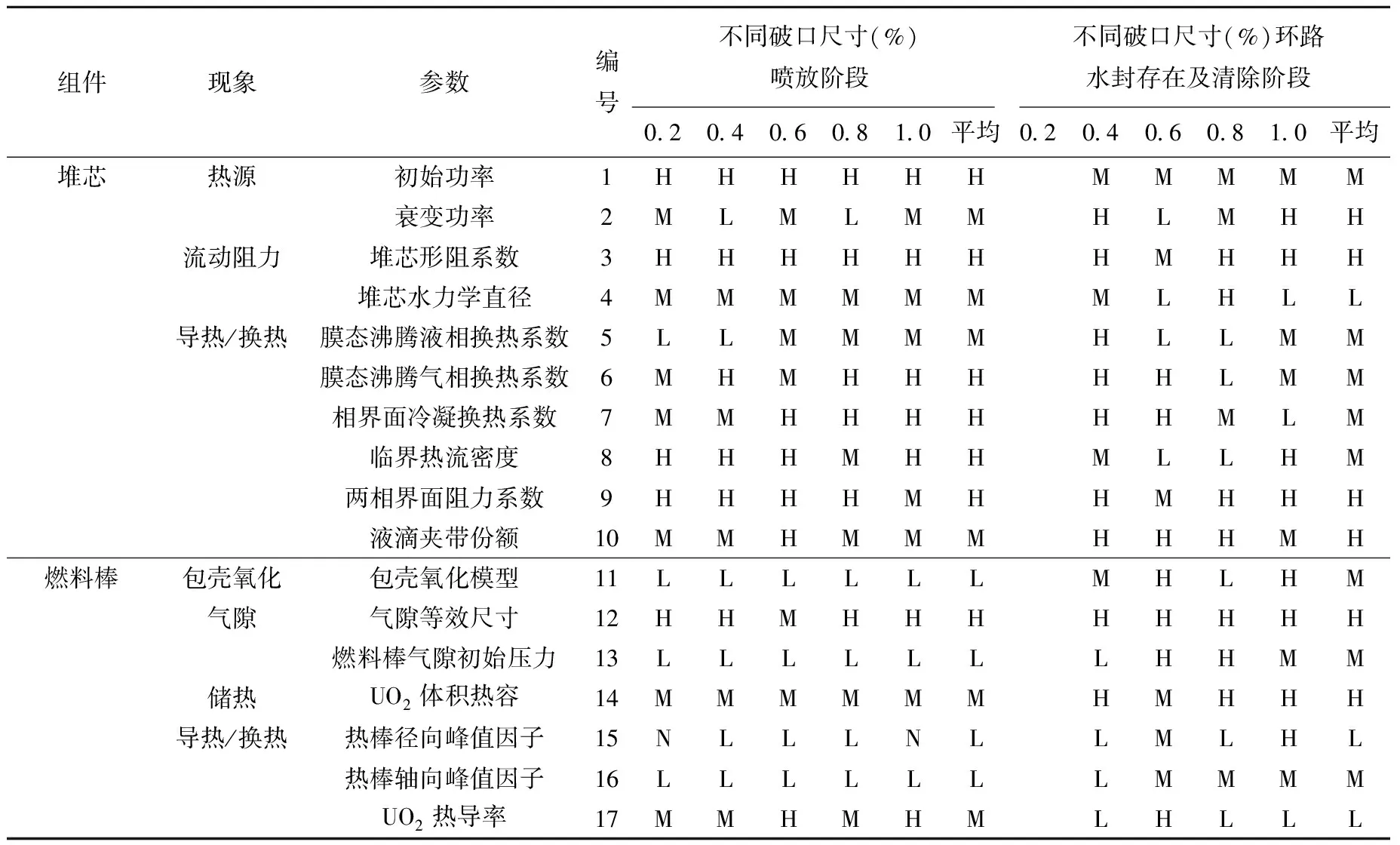
表1 PWR SBLOCA工况参数重要度排序分组表

4 结论

本文研究了在缺乏相应PIRT的情况下确定各输入参数的重要度，选取的研究工况是典型三回路PWR在冷管段发生破口尺寸分别为0.2%、0.4%、0.6%、0.8%和1.0%下的SBLOCA。首先基于基准计算结果，结合已有的SBLOCA PIRT，筛选了可能对FOM，即堆芯活性区MCL，具有影响的54个不确定性输入参数。然后，使用一种优化矩独立全局敏感性分析方法，计算得到了不同破口尺寸下各输入参数对FOM的敏感性度量和重要度排序。将参数的重要度排序转换为Savage分数，按照Savage分数定性地将所有输入参数进行重要度分组，从而得到了PWR SBLOCA的参数重要度排序表。本文提供了一种在缺乏PIRT时识别重要参数的方法。计算结果表明，该文使用的优化矩独立方法能以较小的计算成本完成全局敏感性分析，并能准确地识别对FOM没有影响的输入参数。基于矩独立敏感性分析的计算结果，建立了PWR在SBLOCA下的参数重要度排序表，该表能够在SBLOCA相关分析缺乏PIRT的情况下提供一定的指导和参考价值。敏感性分析结果表明，喷放阶段对MCL影响较大的参数主要为初始功率、初始一回路压力、临界流模型以及一回路中的流动阻力。而在环路水封存在及清除阶段，除破口冷却剂损失外，堆芯液位下降还与堆内沸腾有关，因此界面阻力模型、各种换热模型以及辅助给水系统延迟也对MCL有较大的影响。