高地震烈度、重载大跨桥梁设计关键技术研究

马海忠，熊仕吉，罗 刚，王传波，王照英，江政德，陈建安

（1.华能澜沧江水电股份有限公司如美水电工程建设管理局，云南昆明 650000；2.中国电建集团贵阳勘测设计研究院有限公司，贵州 贵阳 550000）

0 前 言

大跨桥梁具有跨越能力强、施工成本低、结构稳定性好等特点。在其建设中，需从多方面做好配套设计管理等工作。结合如美大桥设计建设情况，重点就其重荷载效应、轴重重载、重载与地震烈度关系等几方面进行研究分析。

1 工程概况

如美大桥是某水电站场内交通桥梁，桥址位置处河流流向N45°E，枯期河水位高程约2612.41m，河面宽66m。大桥所在区域河谷呈“V”型，桥梁分别跨越澜沧江与318国道。该桥主要是为解决某水电站交通运输，最后该桥确定为汽车荷载-80级，验算荷载特-220级，结合现场该桥确定为55m＋90m＋55m连续刚构桥，桥面全宽11.5m，1号墩高31.5m，2号墩高28m，桥梁全长212.8m，该桥址地震基本烈度为Ⅷ度，地震动峰值为0.20g，反应谱特征周期为0.45。

2 场内重载与公路I级荷载对比分析

2.1 场内重载与公路Ⅰ级车辆荷载

JTGD60—2015《公路桥涵设计通用规范》及GBJ22-87《厂矿道路设计规范》代表性的车辆荷载轴重见下文。

2.1.1 公路Ⅰ级车辆荷载

公路Ⅰ级标准车辆荷载轴重、轴距情况见图1。

图1 公路Ⅰ级标准车辆荷载（单位：长度，m；力，kN）

2.1.2 汽车80级车辆荷载

汽车80级荷载标准车辆荷载的轴重、轴距、纵向布置距离等情况如图2所示。

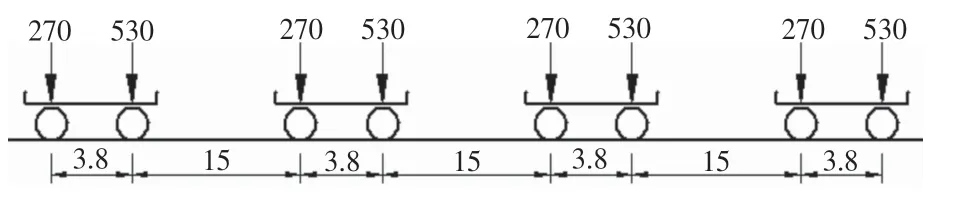
图2 汽车80级荷载标准车辆荷载（单位：长度，m；重量，kN）

从图1～2可知场内重载汽车80级车辆荷载的最大轴重为公路I级车辆荷载的3.79倍，远远大于公路车辆荷载的轴重。

2.2 场内重载与公路I级荷载作用效应

采用MidasCivil（2019）建立桥梁模型，全桥共建立140个单元，145个节点，分别在该模型上进行公路I级与汽车80级荷载的加载计算，确定两者分别产生的荷载效应。

2.2.1 公路I级荷载产生的效应

双车道公路Ⅰ级荷载在跨中产生的最大弯矩为17497.4kN／m，在支点产生最大弯矩34100.9kN／m，最大剪力出现在1 号墩墩顶截面，其值为3156.8kN。

2.2.2 汽车荷载80级产生的效应

汽车荷载80级在跨中产生的最大弯矩为35314.1kN／m，在支点产生最大弯矩81687.5kN／m。最大剪力出现在1 号墩墩顶截面，其值为6448.4kN。

在进行汽车荷载80级与公路I级荷载研究同时，还进行研究了30T梁、40T梁分别在公路I级、汽车-60、汽车-80荷载作用下产生效应，结果如表1～2所示。

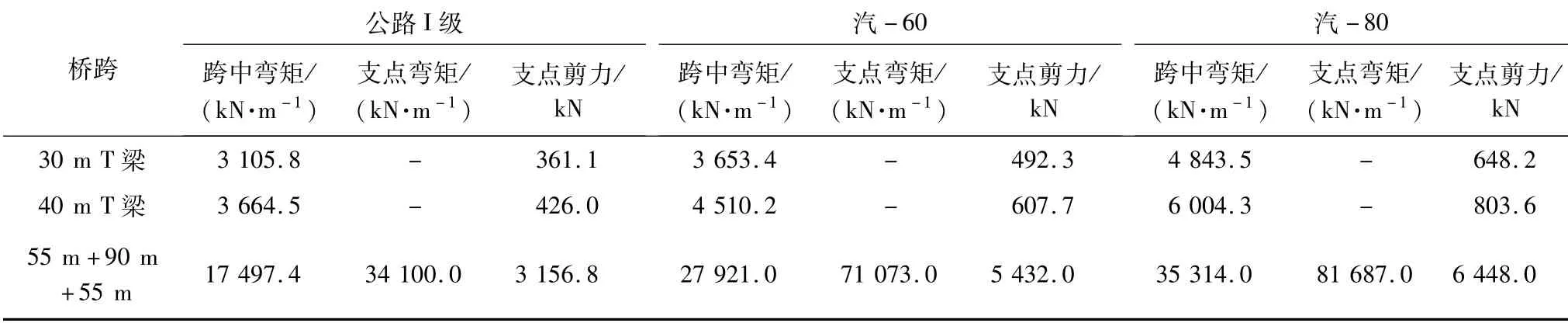
表1 汽车活荷载效应

表2 汽车活荷载效应比值

综合上表分析，重载汽-60在30mT梁跨中产生的弯矩是公路I级产生的1.176倍，在支点产生的剪力是公路I级的1.363倍，在40mT梁跨中产生的弯矩是公路I级产生的1.213倍，在支点产生的剪力是公路I级的1.427倍，在55m＋90m＋55m连续刚构跨中产生的弯矩是公路I级产生的1.595倍，在支点产生的弯矩是公路I级产生的2.084倍，在支点产生的剪力是公路I级的1.721倍。

重载汽-80在30mT梁跨中产生的弯矩是公路I级产生的1.56倍，在支点产生的剪力是公路I级的1.795倍，在40mT梁跨中产生的弯矩是公路I级产生的1.639倍，在支点产生的剪力是公路I级的1.886倍，在55m＋90m＋55m连续刚构跨中产生的弯矩是公路I级产生的2.018倍、在支点产生的弯矩是公路I级产生的2.395倍，在支点产生的剪力是公路I级的2.043倍。

3 场内重载作用下结构设计研究

3.1 结构概况

本桥主梁采用单箱单室直腹板箱形截面，箱梁顶宽11.5m，底宽6.5m，顶板悬臂长度2.5m，根部梁高6.3m，跨中梁高3.8m，顶板厚度0.3m，跨中底板厚0.32m，箱梁根部底板厚0.8m，箱梁高度以及箱梁底板厚度均按2次抛物线变化。箱梁腹板厚度1～5号梁段采用0.7m，6号梁段由0.7m直线渐变到0.5m，渐变段长度4m，7～11号梁段采用0.5m，0号节段顶板厚0.5m，底板厚1.1m，腹板厚0.7m，主墩墩顶设置两道厚1.8m的横隔板。箱梁浇筑分段长度依次为13.0m 长0号段＋5×3.5m＋5×4m，边跨中跨合拢段长均采用2.0m，边跨现浇段长8.885m。箱梁采用三向预应力体系。

主墩采用钢筋混凝土双肢薄壁墩，基础采用钻（挖）孔灌注群桩基础。双肢薄壁墩断面为7.7m×1.8m。承台厚度为4.5m，平面尺寸为12.8m×10.1m。单个墩设6根直径2.2m钻（挖）孔灌注桩。

3.2 梁部关键尺寸的研究

关键尺寸包括了梁高尺寸与桥面板厚度的确定。

3.2.1 支点梁高与跨中梁高的确定

由计算分析表明，本桥在重载汽80作用下跨中产生的弯矩是公路I级产生的2.018倍、在支点产生的弯矩是公路I级产生的2.395倍，常规刚构桥根部高跨比一般在1／16～1／20之间、跨中高跨比比一般在1／50～1／60之间，经计算常规桥梁的梁高不能满足规范要求。经过反复调整梁高的计算，得出符合规范要求合理的梁高为跨中3.8m，根部6.3m，该根部高跨比为1／14.28，跨中高跨比为1／23.68。

在满足汽车荷载80级情况下，该梁根部高比常规梁高最少高出12%，跨中梁高比常规梁高最少高出110%。

3.2.2 梁部环框横向分析研究

重载汽车80级车辆荷载的最大轴重为公路I级车辆荷载的3.79倍，远远大于公路车辆荷载的轴重，需要对常规桥梁结构的桥面板进行承载力分析。

本桥采用MidasCivil（2019）建立桥梁部环框横向模型（见图3），分别在该模型上进行公路I级与汽车80级车辆的加载，确定两者分别产生的荷载效应，从而确定桥面板厚度及配筋。

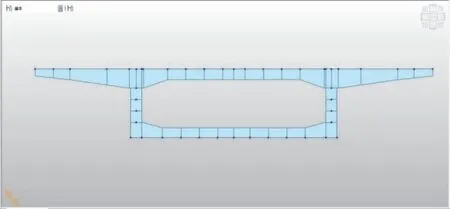
图3 横向计算模型（单位：cm）

（1）公路I级车辆荷载产生的效应

如图3所示，公路I级车辆荷载在桥面跨中产生的最大弯矩为55.7kN／m，在桥面支点产生的最大弯矩为188.9kN／m。

（2）汽车荷载80级产生的效应

如图3所示，汽车80级车辆荷载在桥面跨中产生的最大弯矩为158.9kN／m，在支点产生的最大弯矩为596.0kN／m。

汽车80级车辆荷载在桥面支点的弯矩是公路I级车辆荷载的3.155倍，在桥面跨中的弯矩是公路I级车辆的2.85倍。

桥面板采用横向预应力结构，根据横向计算分析结果，顶板厚度采用30cm，并对横向预应力钢束的配置进行了加强，确保了结构安全。

4 高地震烈度作用下结构设计研究

4.1 模态分析

桥梁结构自振特性参数振型、频率是进行其他动力分析的基础参数，是对结构进行深入动力分析的必备数据。在进行动力分析前，先要进行模态分析，以获取结构动力学基本特征。

本桥采用MidasCivil（2019）软件建立空间动力分析模型，全桥共140个单元，145个节点，将自重及二期恒载转换为质量，同时考虑桩土作用及边墩的作用，采用子空间迭代法，对结构的自振特性进行了计算分析。对于大型的桥梁结构，通常是前几阶自振频率和相应振型起控制作用，因此本文列举了结构前4阶振型、频率及周期。计算结果如图4和表3所示。

由图4及表3计算得到的全桥结构动力特性结果可知：

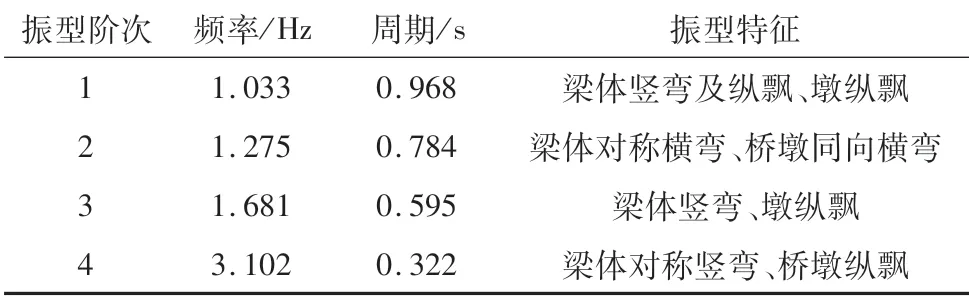
表3 自振特性计算结果

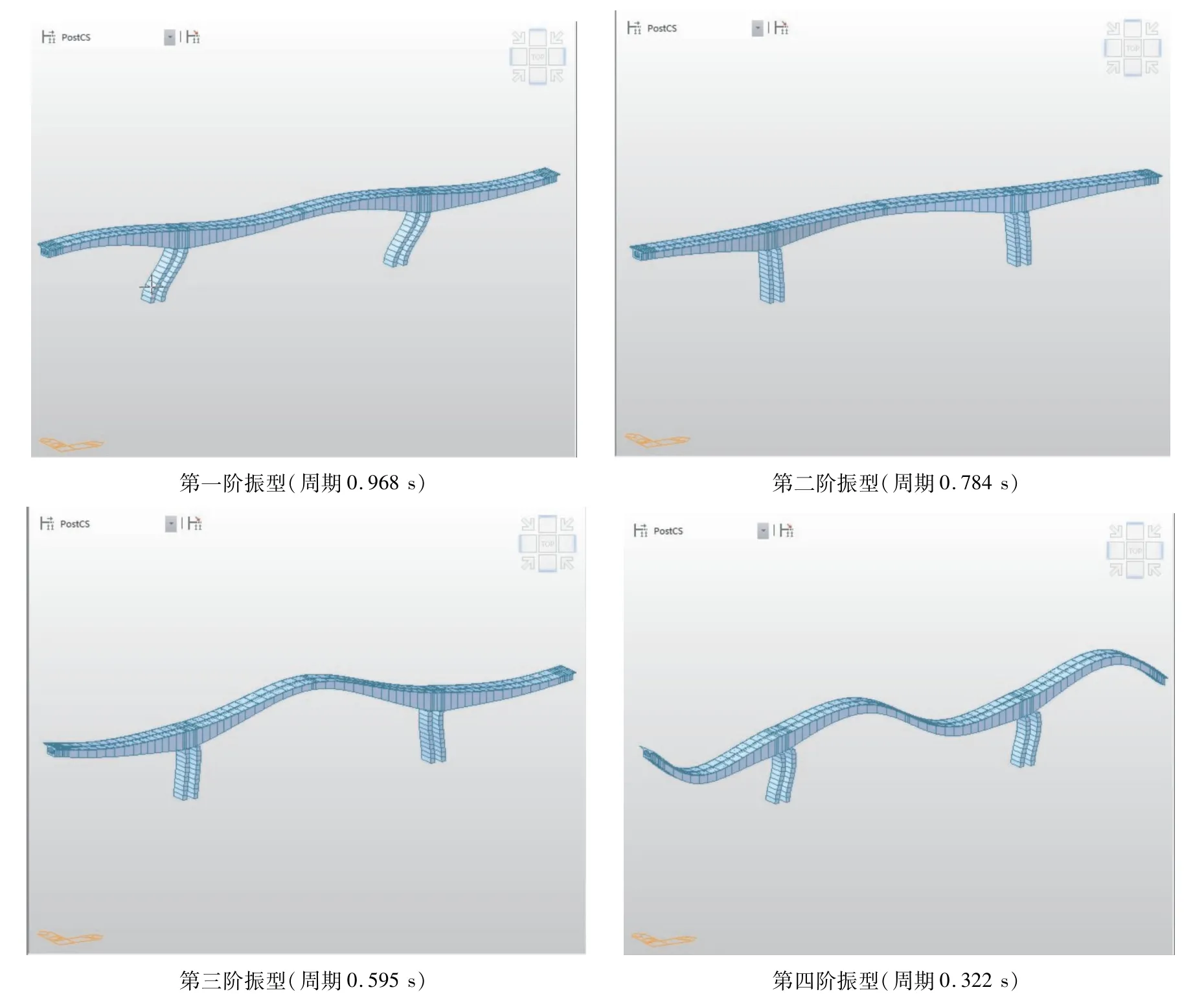
图4 前四阶振型

（1）桥梁结构第1阶振型出现了主梁纵飘，主墩纵桥向弯曲，结构纵向振动先于横向振动出现，表明结构纵桥向刚度较弱。

（2）桥梁结构在第2阶出现了主梁横桥向弯曲与主墩横桥向侧弯。

4.2 地震作用反应谱

地震作用反应谱分析本质上是一种拟动力分析，首先使用动力方法计算质点地震响应，并使用统计的方法形成反应谱曲线，然后再使用静力方法进行结构分析。本桥依据JTG／T2231-01—2020《公路桥涵抗震设计规范》。

抗震计算模型采用MidasCivil（2019）建立，墩梁固结处按刚性连接模拟，支座按实际位置建立节点加弹性连接模拟。

地震动参数输入，根据GB18306—2015《中国地震动参数区划图》及《如美大桥勘察报告》，桥址区地震动峰值加速度为0.2g（对应的地震基本烈度为Ⅷ度），地震动反应谱特征周期为0.45s，得到反应谱曲线如图5所示。

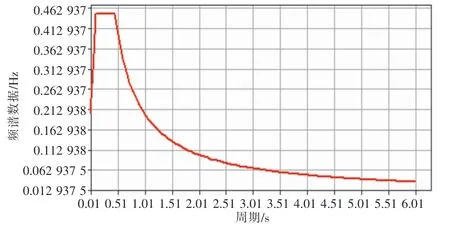
图5 反应谱曲线

4.3 位移响应分析

在水平地震作用下结构关键位置位移影响结果见表4。

由表4可知，结构在水平地震作用下，最大横向和竖向位移均出现在主跨跨中，横向为62.326mm、竖向为11.478mm，最大纵向位移出现在边跨跨中其值为50.154mm。

4.4 内力响应分析

最不利截面出现在墩底，内力响应结果见表5。

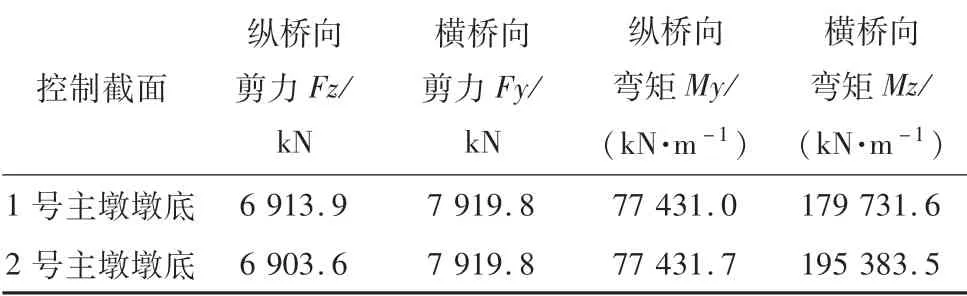
表5 内力响应结果

重载作用下大跨结构的上部结构尺寸较常规桥梁有较大幅度的增加，这导致高烈度地震的作用下桥墩地震内力响应随之增大，因此，在高烈度地震作用下，对重载桥梁的下部结构进行加强，墩身尺寸为2m×1.8m×7.7m，受力主筋采用HRB500高强钢筋，并采用减隔震支座，以此满足抗震要求。

5 结 语

（1）重载荷载效应随桥梁跨度增大而增大，在常规中小跨度时可考虑采用加强配筋解决结构承载力问题，当采用大跨结构时需要提高梁部截面尺寸满足承载力要求。

（2）重载汽车车辆荷载的轴重远远大于公路车辆荷载的轴重，需要对常规桥梁结构的桥面板进行承载力分析，对桥面板进行加强设计。

（3）重载作用下大跨结构的上部结构尺寸较常规桥梁有较大幅度的增加，导致高烈度地震的作用下桥墩地震内力响应随之增大，因此，在高烈度地震作用下，对重载桥梁的下部结构钢筋进行加强，以满足抗震要求。

（4）如美大桥桥区地震烈度为Ⅷ度，荷载等级为汽车-80级，为典型集重载和高地震烈度为一体的大跨度桥梁，可为后期类似重载大跨桥梁借鉴。