秸秆还田机螺旋横刀优化设计与试验

祝英豪，桂真亮，夏俊芳，王万章，朱晨辉

(1.河南农业大学机电工程学院，河南 郑州450002；2.华中农业大学工学院，湖北 武汉 430070)

土壤耕整的目的是为后续作物提供优质种床，在农业工序中是一项工艺复杂、耗时耗能的重要环节[1-4]。触土部件是耕整机的核心，常以切削、翻转、挤压和抛洒等形式作用于土壤，其结构参数和工作参数与土壤形变及位移密切相关，是影响耕整质量及动力需求的关键因素[5-6]。因此，通过参数优化实现增效降阻是触土部件研究的主要内容[7-10]。旋耕作业利用旋转刀辊进行土壤耕整，应用广泛，不仅能破茬还田和平整细碎表土[11-12]，通过对关键刀具改造或位置配置设计，还能用于开沟[13-14]、筑埂[15]和清茬[16]等。常见的旋耕刀具以直角刀、弯型刀和凿型刀为主，但是在使用时均不能有效阻隔作物秸秆与刀轴的接触，尤其对于水稻和小麦等柔性茎秆，存在刀轴被秸秆缠绕导致刀辊堵塞的风险[17]。目前，最常用的刀轴防缠方法包括使用秸秆粉碎装置[18-20]、刀座处加装防缠板(起浆板)[21]以及直接使用大直径刀轴使秸秆长度不足以缠绕刀轴一圈[22]等。然而，当秸秆粉碎质量不达标或留茬过高时，上述防缠方法均有可能失效。于是，将秸秆收集后集中入沟的思路逐渐用于应对播种前的秸秆难题。该类机具通常结构复杂，播种质量受前端秸秆收集装置及后端排秸装置的影响，且功耗较大[23-25]。秸秆还田机的旋埋作业方式另辟蹊径，所使用的组合刀辊是在常规旋耕刀辊内加装螺旋横刀，利用螺旋横刀的旋埋还田效应充分将刀轴与秸秆隔离，既能防缠，又能将秸秆掩埋于土壤之中[26]。因为在此过程中螺旋横刀刃口被秸秆包裹，且刀体轴向径向跨度大，对土壤切削持续时间长，导致切削阻力比常规刀具大很多，所以在不降低螺旋横刀作业效果的前提下降低切削阻力节省功耗是该机具在应用中需要解决的重要问题。本研究在张居敏[27]和张秀梅[28]对高茬秸秆还田机研究的基础上，进一步将螺旋横刀参数化并对土壤秸秆切削过程建模，根据静态及动态参数的分析结果，提取相关变量，开展优化试验研究，揭示各因素与指标之间的一般变化规律，并寻求最优参数，以期解决螺旋横刀现存问题，为高茬柔性秸秆地的耕整提供优质装备。

1 秸秆还田机的结构与工作原理

秸秆还田机适用于高留茬柔性秸秆地的耕整，其结构如图1所示。整机除刀辊外与普通侧边传动旋耕机相同，其刀辊主要由螺旋横刀、弯刀和旋耕刀组成。在刀辊中，弯刀焊接于螺旋横刀两侧，用于螺旋横刀的安装固定。相互匹配的旋耕刀与螺旋横刀旋向相反，且旋耕刀旋转半径较大，用于螺旋横刀的预破茬松土。螺旋横刀是秸秆旋埋还田机的核心作业刀具，承担秸秆掩埋的重要任务。由于螺旋横刀耕幅较宽，刀刃滑切角较小且两端装有弯刀限位装置，秸秆与刀刃接触后不易滑离。耕整时随着刀辊转动，秸秆逐渐包裹螺旋刀刃口，一部分在土壤的支撑下切断，其余秸秆被螺旋横刀压入土壤，在与土壤的相互揉搓中撕裂破碎，螺旋横刀出土拨动并抛起未被土壤覆盖表层完全掩埋的秸秆，完成秸秆还田作业。在此过程中，由于首尾相连的螺旋横刀构成横向封闭结构，秸秆随螺旋横刀在刀辊外围运动，保障了刀轴不被秸秆缠绕。

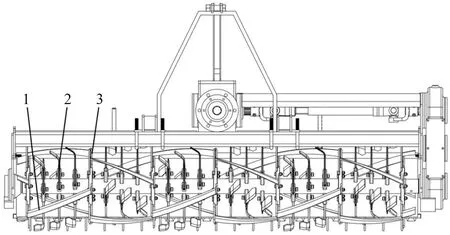
注：1.螺旋横刀;2.旋耕刀;3.弯刀。Note:1.Helical blade;2.Rotary blade;3.Bent blade.图1 秸秆还田机的结构Fig.1 Structural drawing of straw returning machine

2 秸秆还田机螺旋横刀的建模与优化分析

2.1 螺旋横刀几何模型

螺旋横刀为大螺距圆柱螺旋体，各棱边均为圆柱螺旋线，如图2所示。对螺旋横刀进行坐标系建模，其中，螺旋横刀左端面ABCDE所在平面为坐标系Oxy平面，螺旋轴线OO'与z轴重合。螺旋横刀两端面的间距L为刀具长度，其值由机具的整体幅宽决定；AE边与BC边夹角为刃磨角β，两边所形成的楔形结构有利于土壤的切削剥离；AE边长度为刀具宽度W，AE边与x轴的夹角为前角θ，这两者共同决定刀具转动时对土壤的扰动能力；当W越大或θ越小时，因螺旋横刀旋切作用而被挤压带动直至抛起的土壤越多，该指标由相对抛土宽度Wp表示，计算公式见公式(1)。前角θ决定了螺旋横刀切土时的姿态，其值越大，表明刀具越趋近于竖直状态切削土壤。刃口A最先接触土壤直至整条刀刃入土，此时螺旋横刀转动的角度为刀具的跨度角αL，而刀具螺旋升角δ为刀刃螺旋线的切线与垂直螺旋线轴线平面的夹角，可由跨度角αL、刀具长度L和刃口A的旋转半径R表示，如公式(2)所示。

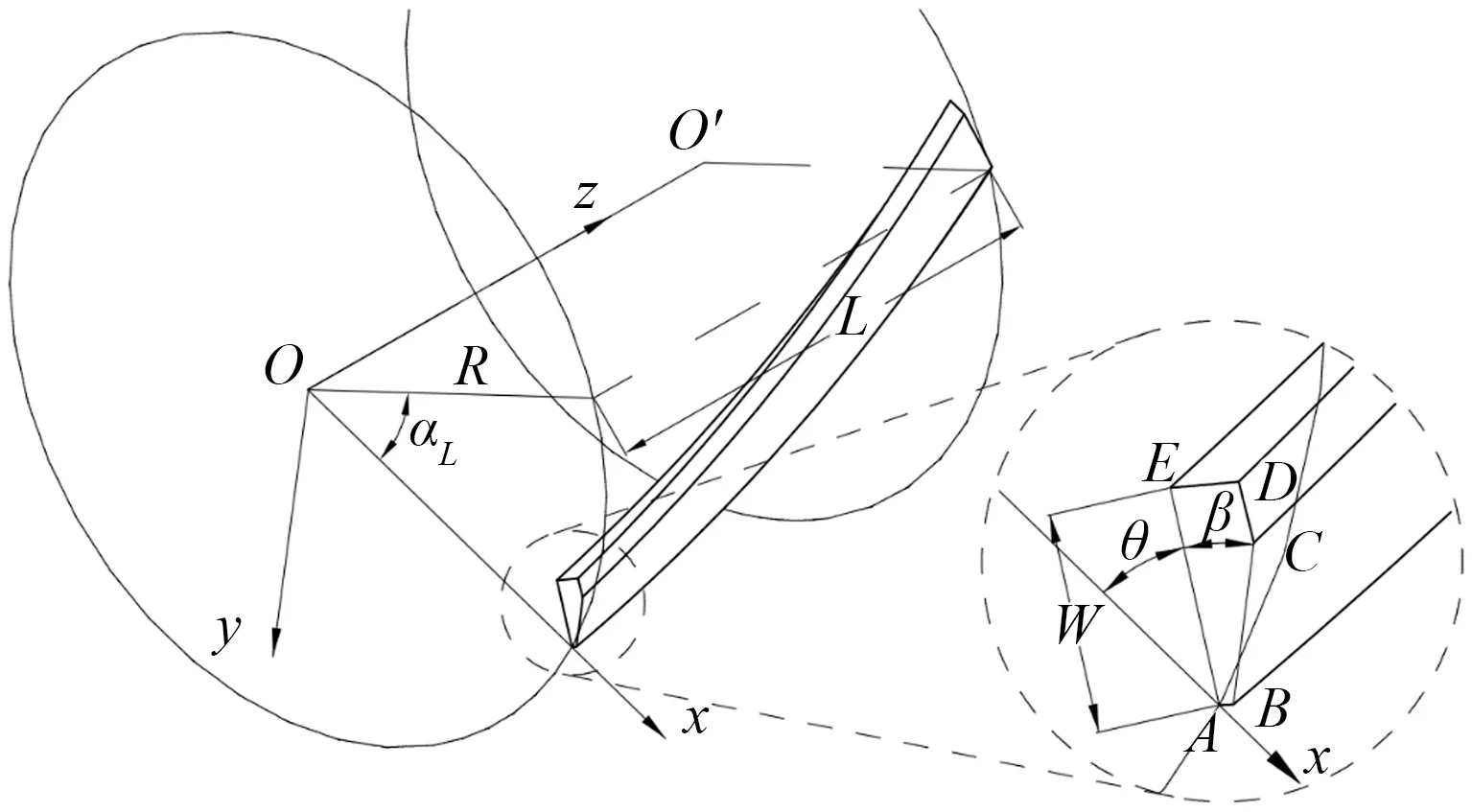
图2 螺旋横刀的坐标系建模Fig.2 Coordinate model drawing of helical blade

Wp=Wcosθ

(1)

(2)

2.2 螺旋横刀旋切土壤过程分析

螺旋横刀的作业是由绕刀轴的圆周速度vω(vω=ωR，ω为角速度，r·s-1)与沿作业方向的前进速度vm组成的复合运动，则刀刃动态旋切轨迹方程公式如下所示。

(3)

式中：α为螺旋横刀任一截面所对应的位置角。

刃口A所在端面的位置角α为0°，则刃口A的动态旋切轨迹方程公式如下所示。

(4)

根据公式(4)绘制刃口A的旋切轨迹，如图3所示。Q点所在的位置转角φ为0°，随着螺旋横刀转动，刃口A依次经过Q1、Q2、Q3和Q4直至完成一圈并进入下一个周期。为保证螺旋横刀入土切削时刀背不推压未耕土壤，出土时不向前抛土，要求刃口在旋切过程中切削速度始终无水平向前的分量，因此判断Q1和Q3分别为入土临界点和出土临界点，Q2为耕整时最低点，与Q1和Q3在竖直方向上的距离H为螺旋横刀理论上的最大耕深。直线LO为旋转中心O的运动轨迹，LP为切削速度v瞬心P的运动轨迹。由于切削轨迹上任意位置点Q与其旋转中心O和切削速度瞬心P形成的位置三角形与该位置处的速度矢量三角形相似，因此，H计算公式如下所示。

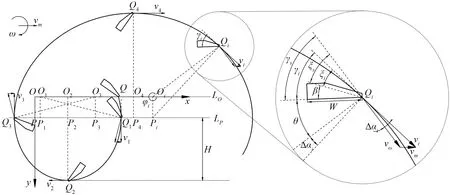
图3 螺旋横刀刃口A旋切轨迹Fig.3 Trajectory diagram of point A of helical blade

(5)

式中：λ为旋耕速比，即圆周速度vω与前进速度vm的比值。

根据参考文献[29]可知，静态切土角γs为AE边与圆周速度vω的夹角，其值与前角θ互余；动态切土角γ为AE边与切削速度v的夹角。因此，静态隙角ξs与动态隙角ξ如下所示。

ξs=γs-β

(6)

ξ=γ-β

(7)

在位置三角形中根据正弦定理，转角φ与速度夹角Δα的关系如下所示。

(8)

所以动态切土角如下所示。

(9)

根据公式(9)，将φ与λ视为函数γ(φ,λ)的自变量，分别对φ与λ求导。

(10)

从公式(10)中可以获取γ随φ与λ的变化趋势，如图4所示。

图4 螺旋横刀动态切土角的变化曲线Fig.4 Variation curve of dynamic cutting angle of helical blade

假定耕深h=H，入土点Q1的切土角最小，γ1=γs-φ1，其中φ1=arcsin(1/λ)；出土点Q3的动态切土角最大，γ3=γs-φ3+180°，其中φ3=180°-arcsin(1/λ)。螺旋横刀由入土至出土，切土角持续递增，当速比较小时，会增加动态切土角在其静态值的上下波动范围，极易出现负隙角现象，同时切土节距增加，会导致入土阻力过大。切土角与切土阻力并非呈单调关系。当切土角过小时，导致隙角不足，引起刀背推压摩擦土壤，切土阻力急剧增加；当切土角较大时，则前角过小，螺旋横刀内切面以趋于平压的方式作用于土壤，刀刃失去作用，同样造成切土阻力增加。因此，静态切土角的设置受隙角和前角影响。

从Q1运动至Q3，螺旋横刀先向下切出土垡，然后刀身上提，直至土面抛撒土壤，此过程动态切土角逐渐增大，内切面逐渐趋于切削速度的垂直方向，内切面在土壤中的姿态由利于切土向利于抛土转变，因此将耕整过程分为切土行程与抛土行程。如图5所示，切垡末点的转角为φN，此时刃口位置QN即可视为切土行程与抛土行程的分界点。

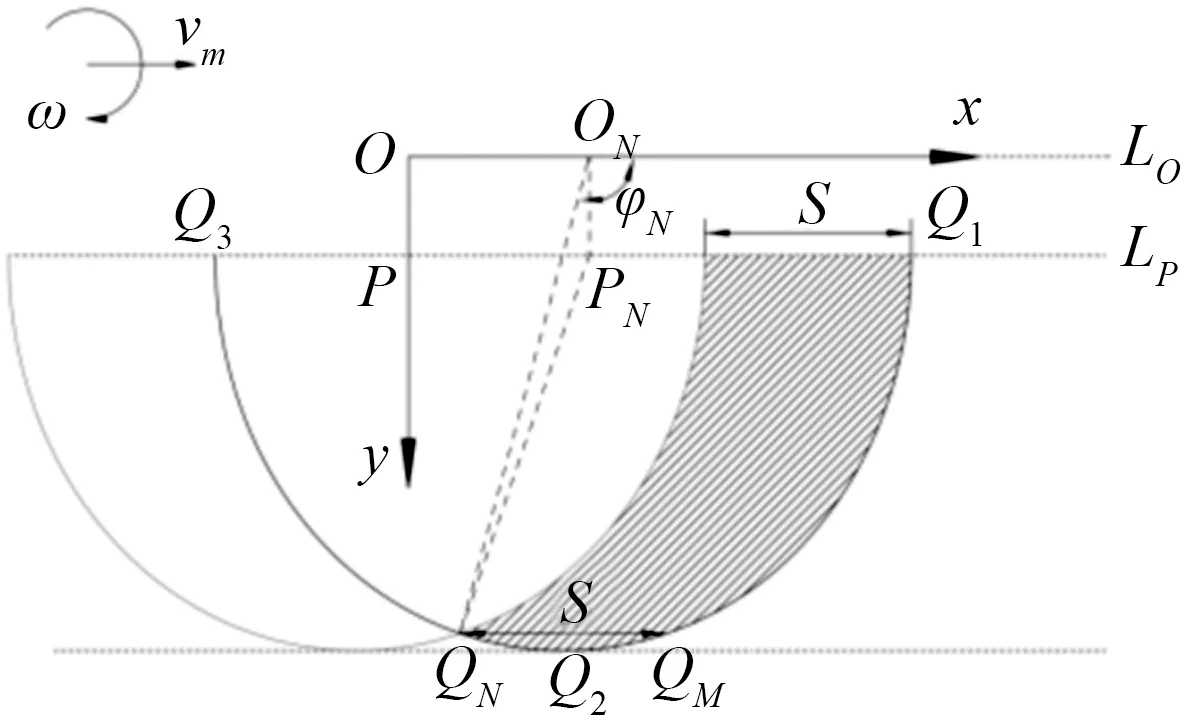
图5 螺旋横刀切土行程与抛土行程示意图Fig.5 Diagram of cutting and throwing soil process of helical blade

根据QN与QM的横坐标之差为节距S，切垡末点的转角φN如下所示。

(11)

式中：z为刀辊一周安装螺旋横刀的数量。

切土行程作业对象为未耕实土，在选用较小动态切土角时，需首先满足入土隙角ξ1>0°的要求；抛土行程作业对象为已耕松土，能允许较大的动态切土角，但应保证刃口率先出土。

2.3 螺旋横刀优化参数确定

根据上述参数表达式及分析，螺旋横刀的结构参数主要由刃磨角β、前角θ以及刀具宽度W组成。在螺旋横刀的第一次参数优化中将刃磨角、前角、刀具宽度数值从35°、17°、25 mm设置为18°、35°、35 mm，减小刃磨角，增大前角大幅降低了耕整阻力，增大刀具宽度弥补了前角增大引起的抛土宽度不足。鉴于18°的刃磨角已经接近设计参考的最小值，且前角与刀具宽度对螺旋横刀的切土与抛土性能影响明显。因此，选择前角与刀具宽度进行参数优化，在不降低工作性能的前提下降低切削阻力节省功耗。

目前，螺旋横刀锻造模具螺旋槽的最大宽度为36 mm，则刀具宽度的设计值应小于36 mm。旋耕作业常用的速比λ=4～10[30]，根据公式(8)和公式(9)计算，动态切土角相对于静态值的最大波动范围为±14.48°。由公式(12)可知，静态切土角的范围为75.52°>γs>32.48°，则57.52°>θ>14.48°。

(12)

3 秸秆还田机螺旋横刀参数优化研究

3.1 螺旋横刀结构参数优化试验

3.1.1 试验条件 试验在华中农业大学油菜全程机械化科研基地进行，试验所用土槽长×宽×深为1 200 mm×1 000 mm×500 mm，有效行程1 000 mm，土壤按照m(沙土)∶m(黏土)=1∶1混合，含水率为25.41%，土壤容重为1.53 g·cm-3。试验设备如图6所示。旋耕组件、升降组件和行走组件各由1台电机独立提供动力，试验刀辊为图1机具组合刀辊中的1段，幅宽为370 mm。试验前进速度为0.6 m·s-1，旋耕转速为240 r·min-1，作业耕深为150 mm。

注：1.控制柜；2.机架；3.动态扭矩传感器；4.轨道；5.旋耕组件；6.行走组件；7.升降组件。Note:1.Control cabinet;2.Frame;3.Dynamic torque sensor;4.Track;5.Rotary tillage component;6.Walking component;7.Jacking component.图6 土槽试验旋耕台车Fig.6 Rotary tillage trolley for soil-bin test

3.1.2 试验指标和方法 本研究选取刀辊作业扭矩和秸秆埋覆率作为试验指标。扭矩值是衡量刀辊耕整阻力的参数，由于本次试验运动参数始终不变，因此扭矩值也可衡量各组试验的功耗及能耗。利用动态扭矩传感器(北京中航科仪测控技术有限公司，转速测量范围0～4 000 r·min-1，扭矩测量范围0～500 N·m)测量刀辊扭矩，经采集卡采集后，通过wifi模块传递数据并储存在笔记本电脑中。秸秆埋覆率通过计算得到。在每次耕整行程中相隔1 m以上选取3处250 mm×250 mm的区域，每处平铺长20 cm的秸秆150 g，耕整后测量所有土面遗留的秸秆质量，秸秆埋覆率的计算公式如下所示。

(13)

式中：M为秸秆埋覆率；mq为耕前平铺秸秆总质量；mh为耕后土面遗留的秸秆质量。

为了防止土壤中的秸秆干扰后续试验测量结果，尽量将土中秸秆剔出，并使用喷漆对不同组间使用的秸秆进行颜色标记。

3.1.3 试验方案与结果分析 依据上述对螺旋横刀结构参数的分析，确定选取前角和刀具宽度作为试验因素，前角选取4个水平分别为55°、45°、35°和25°，刀具宽度选取3个水平分别为25、30和35 mm，试验现场由图7所示，试验结果见表1。

图7 土槽试验现场Fig.7 Soil-bin test site

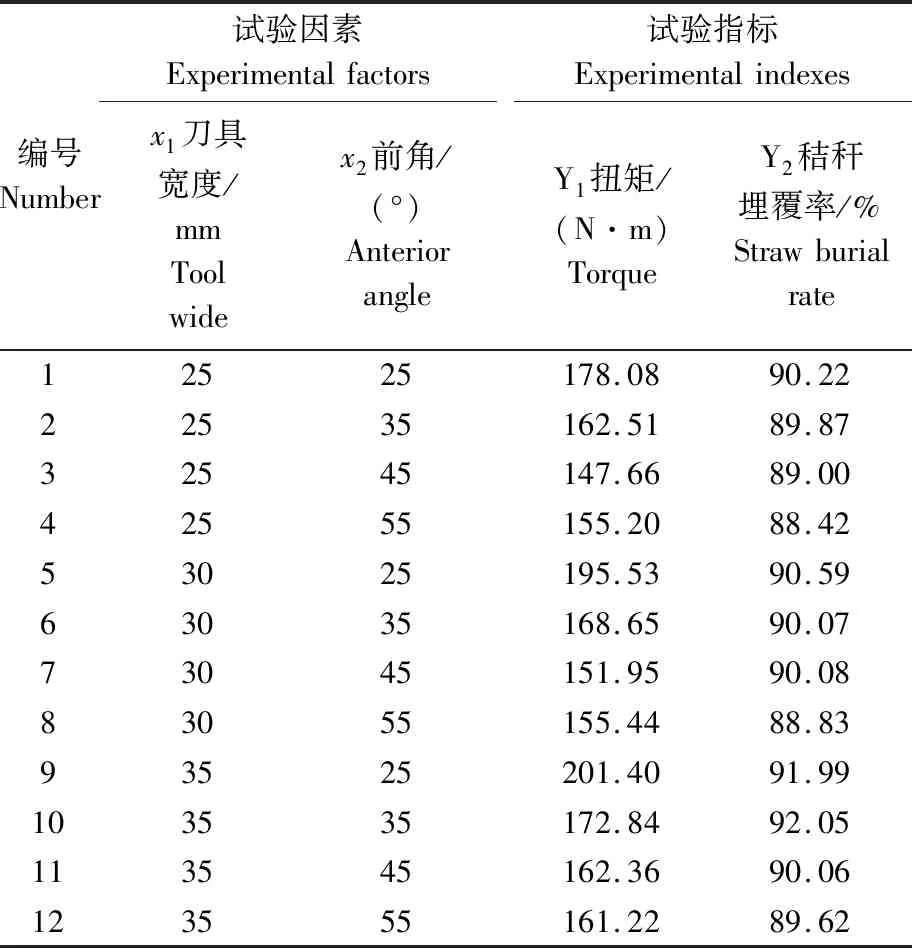
表1 螺旋横刀结构参数优化试验方案与结果Table 1 Structural parameter optimization experiment scheme and result of helical blade

利用Matlab软件对试验结果进行曲面拟合，得到扭矩Y1和秸秆埋覆率Y2共2个试验指标的拟合方程(14)及(15)，确定系数R2分别为0.98和0.92，说明拟合方程对试验值的拟合程度较好。

Y1=210.422 5+5.078 0x1-5.909 4x2-0.032 22x1+
0.073 52x2-0.046 2x1x2

(14)

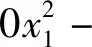
(15)

对于扭矩Y1，刀具宽度与前角的拟合曲面如图8-a所示。当刀具宽度一定时，扭矩Y1随前角的增大呈现先减后增的趋势，原因是前角较小时，静态切土角较大，造成切土阻力增加，随着前角继续减少，这种情况逐渐改善；当前角减小到入土时动态隙角不足时，切土阻力开始增加。当前角一定时，扭矩Y1随刀具宽度增加而增大，螺旋横刀与土壤的作用面积随刀具宽度增加而增大，尤其在抛土行程更加明显。从变化速率上看，扭矩Y1对前角更加敏感，侧面反映抛土宽度对扭矩Y1的影响不大，切土阻力远大于抛土阻力。

对于秸秆埋覆率Y2，刀具宽度与前角的拟合曲面如图8-b所示。随着刀具宽度的增加和前角的减小，秸秆埋覆率Y2均为递增状态，原因是刀具宽度与前角的上述变化会加长出土时的动态抛土宽度，抛土量的增大使更多未完全压覆的秸秆被土壤覆盖。

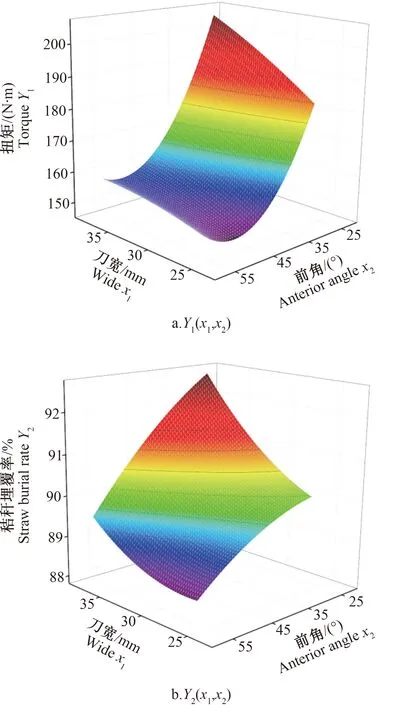
图8 螺旋横刀结构优化试验拟合曲面Fig.8 Fitting surface of structure optimization test of helical blade

3.1.4 试验结果 在土槽试验中对螺旋横刀开展结构参数优化的目的是为了获取最优的参数组合，在保证一定秸秆埋覆率的情况下最大限度降低螺旋横刀的切土阻力，根据实际的工作条件与农艺要求，选定试验因素的约束条件如下所示。

(16)

利用Matlab软件对拟合方程进行求解，得到螺旋横刀最佳结构参数。参数优化结果为x1=36.73 mm，x2=51.76°，即螺旋横刀刀具宽度为36.73 mm，前角为51.76°，此时的扭矩为156.69 N·m，秸秆埋覆率为90%。将优化结果圆整后刀具宽度为35 mm，前角为50°。加工该参数的磨具及直刀毛坯，制造螺旋横刀，安装于土槽试验旋耕台车，进行验证试验，得到扭矩为149.24 N·m，秸秆埋覆率为90.53%。扭矩试验值与理论值的误差为4.75%，秸秆埋覆率试验值与理论值的误差为0.59%，误差较小，验证了螺旋横刀结构参数优化的可靠性。

3.2 螺旋横刀工作参数优化试验

3.2.1 试验因素和指标 旋耕的工作参数由前进速度、旋耕转速和作业耕深组成。工作参数决定了刃口运动轨迹、动态参数变动范围、切土节距和出入土时切土角的大小，以上参数与作业质量性能密切相关。因此，将前进速度、旋耕转速和作业耕深作为试验因素。试验选用的刀辊装配优化后的螺旋横刀，土槽中土壤含水率为土壤27.43%，土壤容重为1.62 g·cm-3。试验指标除扭矩和秸秆埋覆率外，额外添加功耗作为描述刀辊动力需求的试验指标，计算公式如下所示。

(17)

式中：Pn为功耗；T为扭矩；n为旋耕转速。

3.2.2 试验方案和结果 根据课题组前期刀辊的试验示范情况，确定运动参数的范围为前进速度0.40～1.00 m·s-1，旋耕转速240～320 r·min-1，作业耕深120～200 mm，开展组合式旋埋刀辊三元二次回归正交旋转组合设计多因素寻优试验，因素水平编码表见表2。

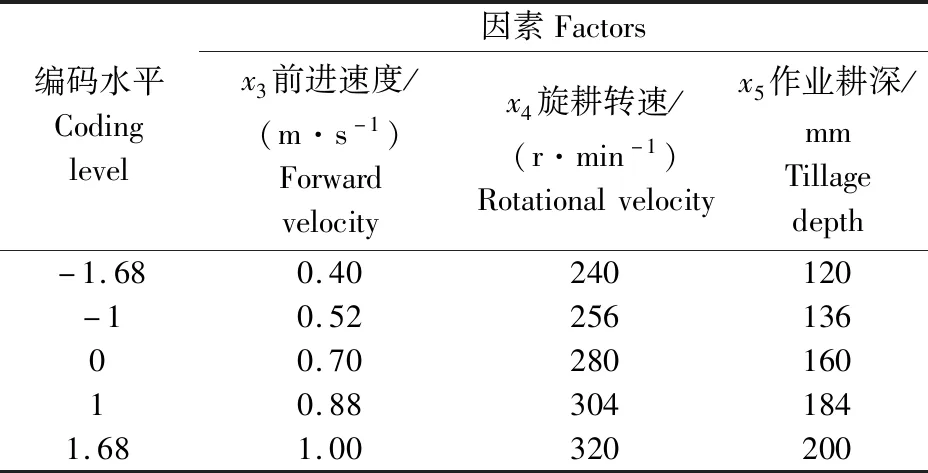
表2 螺旋横刀工作参数优化试验因素水平编码表Table 2 Coding table of optimization test factor and level of working parameter of helical blade

根据试验的设计理论，共进行20组试验，每组重复3次，取平均值作为最终结果，由表3所示。利用Design-Expert软件对结果进行二次回归分析，并进行多元回归拟合，建立扭矩Y1、秸秆掩埋率Y2和功耗Y3分别与前进速度、旋耕转速和作业深度的二次回归模型，并进行方差分析，见表4。

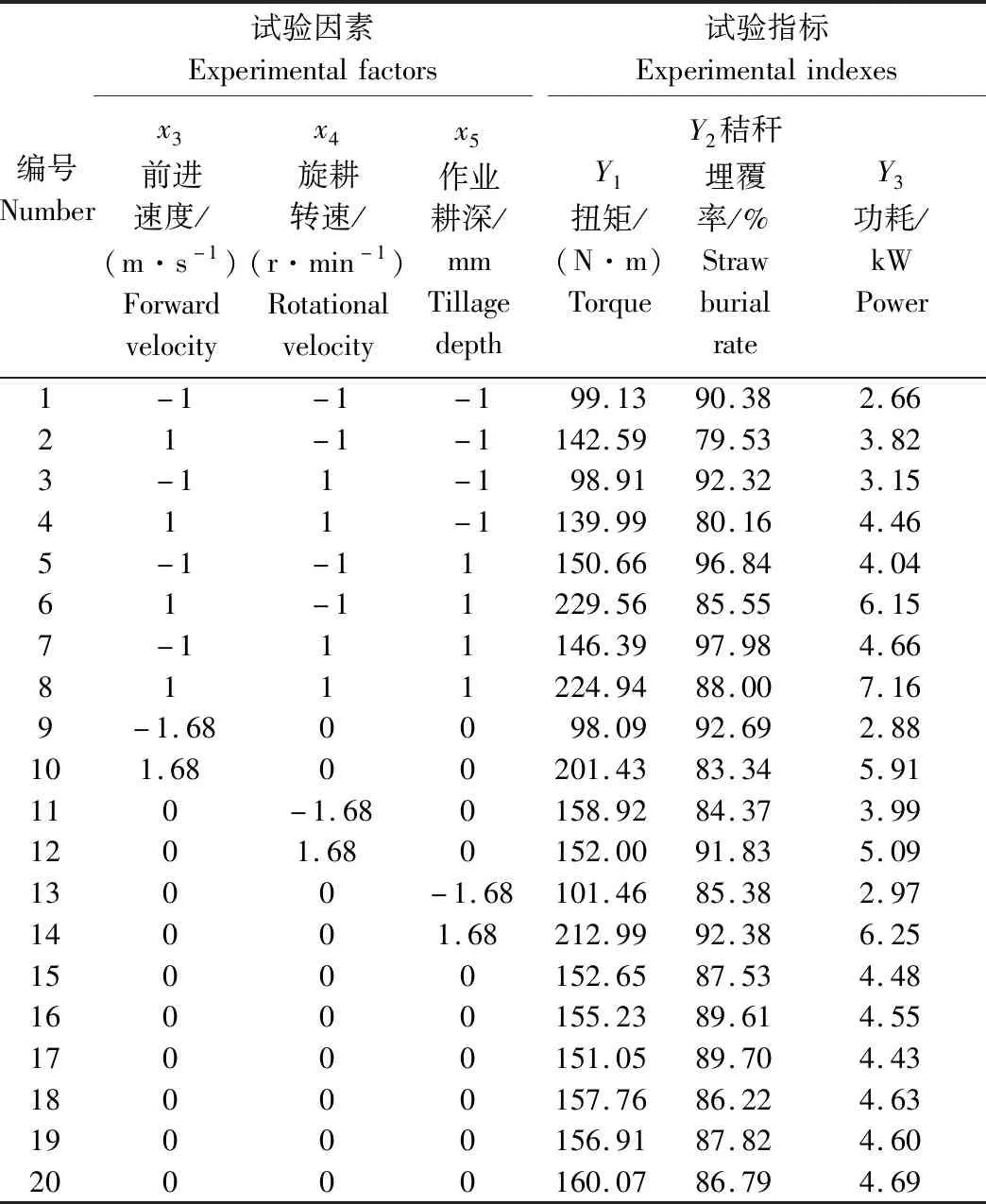
表3 螺旋横刀工作参数正交旋转组合试验设计及结果Table 3 Design and result of experiment of quadratic rotation-orthogonal combination of working parameter of helical blade

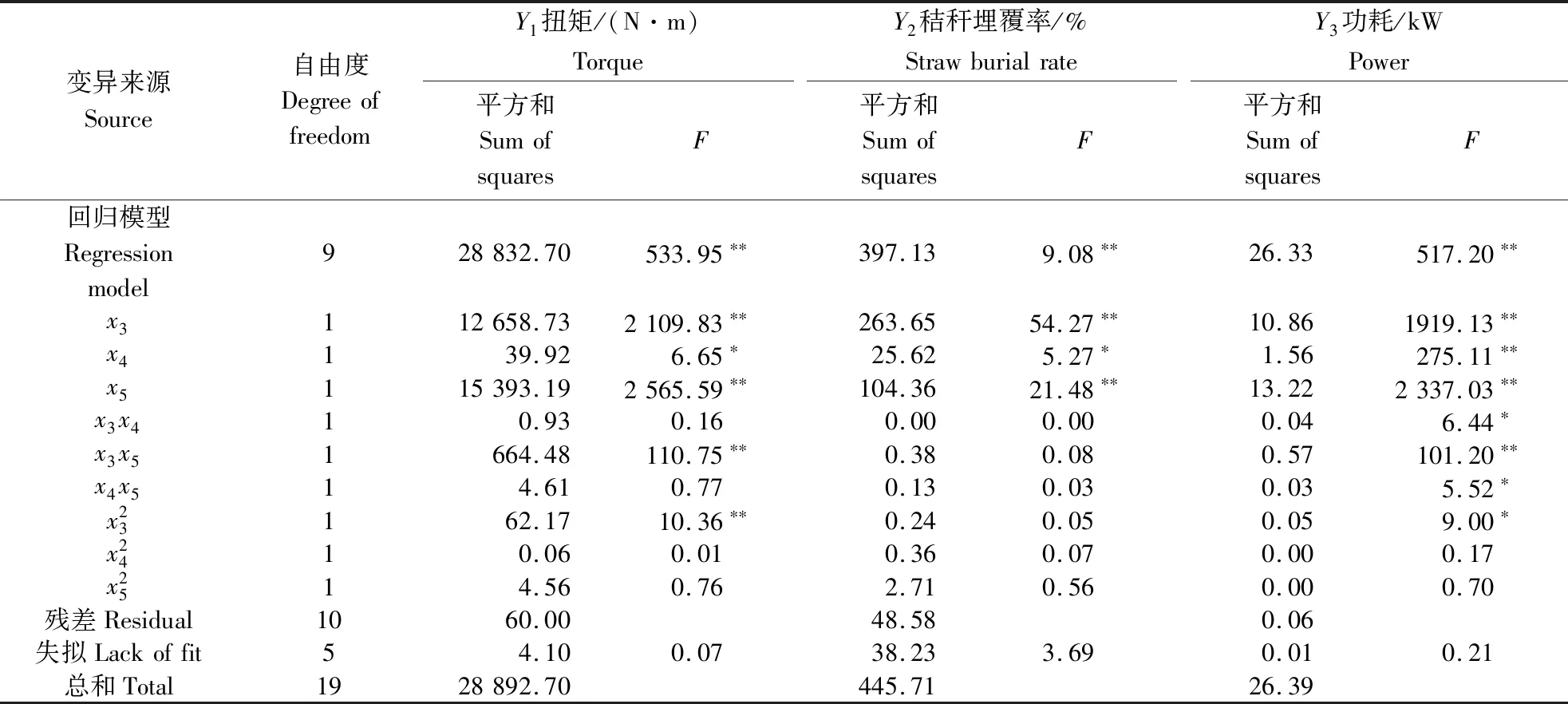
表4 螺旋横刀工作参数正交旋转组合试验方差分析Table 4 Variance analysis of quadratic rotation-orthogonal combination experiment of working parameter of helical blade

由上述方差分析表，扭矩、秸秆埋覆率和功耗回归模型检验均极显著(P<0.01),回归方程失拟不显著。对于各试验指标将显著项主次排列，扭矩为x5、x3、x3x5、x32和x4，秸秆埋覆率为x3、x5和x4，功耗为x5、x3、x4、x3x5、x32、x3x4和x4x5。筛选出显著影响因素，将不显著的交互作用项的回归平方和及自由度并入残差项后，再次进行方差分析，且失拟项均不显著，说明不存在影响试验指标的主要因素，最终得到旋耕性能指标与因素编码值间的回归方程。

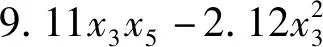
(18)

Y2=88.42-4.39x3+1.37x4+2.76x5

(19)

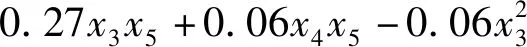
(20)

根据回归方程，当x3、x4和x5在区间[-1.682,1.682]内，通过求导，分析各试验指标与其显著因素之间的增减规律，由表5所示。随着前进速度的减少，各试验指标均向有利的方向变化，但前进速度较小会严重影响旋耕作业效率，根据生产率≥0.6 hm2·h-1的要求[31]，且机具幅宽为2.3 m，经计算前进速度≥0.72 m·s-1。

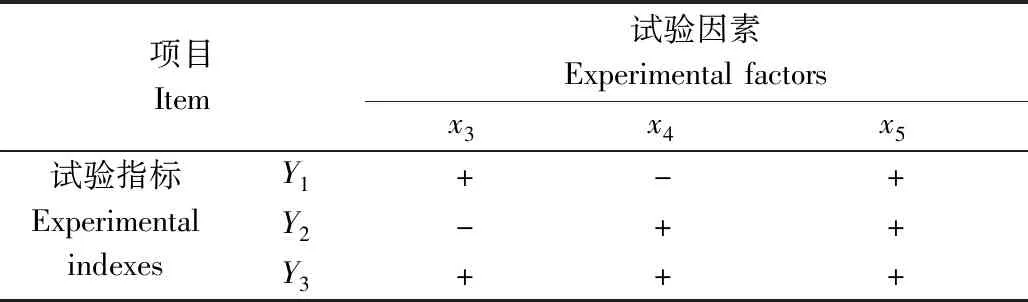
表5 螺旋横刀工作参数试验因素与指标的增减关系Table 5 The increasing and decreasing relationship between experimental factors and indexes of working parameter of helical blade

利用Design-Expert软件中的优化模块对回归模型求解，根据实际工作条件及相关模型的分析结果，选定试验因素的约束条件如下所示。

(21)

对其参数进行求解，当前进速度为0.72 m·s-1，旋耕转速为320 r·min-1，作业耕深为174 mm，刀辊耕整性能达到最优的状态，其扭矩为176.41 N·m，秸秆埋覆率为91.81%，功耗为5.89 kW。

4 田间对比试验

4.1 试验条件

为了检验螺旋横刀优化后的作业性能，开展田间对比试验。试验田为黏性土壤，20 cm处坚实度为937 kPa，含水率为33.65%，密度为1.75 g·cm-3；田间为绿肥，高度为84.5 cm，茎秆量为1 286 g·m-2，含水率为60.15%。作业机具由东方红LX954轮式拖拉机驱动，根据土槽试验的运动参数优化结果，使用低速2档，前进速度为0.65～0.75 m·s-1，输出转速设置为720 r·min-1，经机具减速箱后旋耕转速为324 r·min-1，每次试验重复3次，每次作业行程>20 m，整个试验保持18 cm的耕深不变。试验指标为秸秆埋覆率和功耗，测试方法参考文献[26]。

4.2 试验结果与分析

螺旋横刀优化前(刀具宽度35 mm，前角35°)秸秆埋覆率为83.27%，功耗为41.8 kW；优化后(刀具宽度35 mm，前角50°)秸秆埋覆率为83.67%，功耗为37.6 kW。从秸秆埋覆率来看，抛土宽度发生变化但埋覆率并没有明显区别，这与土槽试验结果不一致。一方面，茎秆过长，还田难度加大，导致秸秆埋覆率整体不高；另一方面土槽土壤混有沙土，含水率低且反复耕整，导致土壤较松散。改变抛土宽度有利于控制抛土量，但田间土壤含水率高，黏塑性强，抛起后不易散开。土槽试验整个过程秸秆埋覆率上下浮动小于5%，因此与抛土相比，秸秆埋覆主要靠螺旋横刀的压埋作用。从功耗来看，优化后切土角减小，切土阻力降低，功耗降低10.05%。综上所述，螺旋横刀的优化达到了保持原有作业效果的前提下降低功耗的目的。

5 结论与讨论

本研究通过建立螺旋横刀的参数化模型，分析刃口运动轨迹，得出螺旋横刀动态参数的方程表达式以及随转角的变化曲线。结果表明，螺旋横刀由切土转向抛土的过程中，动态切土角不断增大，有利于旋耕增效减阻，且动态参数是以静态值为基准上下变动，其范围大小由速比决定。基于螺旋横刀旋切土壤过程分析，借助土槽试验平台，开展螺旋横刀结构参数(刀具宽度、前角)优化和作业参数(前进速度、旋耕转速、作业耕深)匹配。通过全面试验建立刀具宽度与前角分别对扭矩与秸秆埋覆率的拟合方程，并绘制拟合曲面，分析各因素对指标的影响规律。结果显示，扭矩随刀具宽度增加而增大，随前角增大而先减后增；秸秆埋覆率随刀具宽度增加和前角减小而呈递增趋势。进一步结合约束条件，最终确定螺旋横刀的最优结构参数组合为刀具宽度35 mm，前角50°。通过开展三元二次回归正交组合试验对螺旋横刀的作业参数进行匹配，基于对回归方程的求导分析，得到各工作参数与试验指标的增减变化关系，借助Design-Expert软件中的优化模块对回归模型求解，得到最优工作参数为前进速度0.72 m·s-1，旋耕转速320 r·min-1，作业耕深174 mm，此时刀辊扭矩为176.41 N·m，秸秆埋覆率为91.81%，功耗为5.89 kW。在最优作业参数下，进行田间对比螺旋横刀结构参数的优化效果，结果显示，优化前后秸秆埋覆率相差不大，结合土槽试验抛土宽度变化对秸秆埋覆率的影响小于5%的分析结果，表明秸秆埋覆功能主要靠螺旋横刀转动时的压埋作用，抛土埋覆作用较弱。优化后刀辊功耗降低10.05%，因此螺旋横刀的优化达到了保持原有秸秆埋覆效果的前提下降低功耗的目的。

秸秆旋耕埋覆主要依靠刀具的压埋作用和抛土作用。本研究发现，改变影响螺旋横刀抛土量的刀具宽度参数后，其对应的秸秆埋覆率指标变化并不明显，说明螺旋横刀主要靠压埋作用进行田间高茬秸秆处理，这与张居敏等[29]通过螺旋横刀滑切角分析秸秆埋覆机制的研究结果一致。为进一步增加埋覆效果，张居敏等[29]主张维持较大的切土角，即较小前角以增加抛土宽度，来强化螺旋横刀出土时的上扬抛土性能，而本研究发现前角对旋耕阻力的影响十分显著。通过抛土略微增加秸秆覆盖效果会导致阻力大幅增加，对螺旋横刀的应用十分不利，这也是优化前该刀具只能应用于水田的主要原因。