基于SolidWorks的渐开线齿轮参数化精确建模*

崔玉芝，王仲勋，蒲洁涛，杜宗霖，娄红杰

(1.烟台职业学院 机械工程系，山东 烟台 264670；2.山东景芝建设股份有限公司，山东 潍坊 262100；3.山东乐普韦尔自动化技术有限公司，山东 济南 250002)

0 引言

齿轮机构可以用来传递空间任意两轴之间的运动和动力，其圆周速度可达到300 m/s，是现代机械中应用最广泛的一种传动方式[1],可以实现同向和逆向传动、平行轴传动、相交轴传动或交错轴传动,具有传动功率范围大、效率高、传动比准确、使用寿命长、工作平稳和工作安全可靠等特点。齿轮的种类较多，按齿廓曲线的形状齿轮划分为渐开线、摆线和圆弧齿轮三种，其中渐开线齿轮制造比较容易且传动更平稳，应用最广泛[2]。但是，在实际设计中渐开线齿轮的精准造型是一大难点，主要在于齿廓渐开线草图的绘制。

传统的齿轮设计过程繁琐，齿形精度低，设计用时长。随着计算机辅助设计和制造技术的发展，利用一些三维设计软件进行齿轮设计可节约设计时间，同时能保证齿形的精度，预测齿轮装配时的干涉现象。现阶段基于SolidWorks软件的造型方法主要有使用SolidWorks Toolbox插件等设计库调用齿轮，通过修改部分已设定的参数获得需要的齿轮，这种方法适用于对渐开线精度要求不高、简单的齿轮传动运动分析或简单的机构绘制等[3]。也可以使用CAXA电子图板、GearTrax、Pro/E和迈迪工具集生成齿轮[4,5]。利用圆弧或直线拟合渐开线或齿根过渡曲线，生成的轮齿表面轮廓均为近似渐开线，齿廓精度较低，不利于后续的齿轮动态仿真及有限元分析。

本文基于三维设计软件SolidWorks和齿轮参数公式、渐开线公式，结合软件方程式功能，实现了渐开线齿轮参数化精确建模。参数化设计主要利用草图设计、尺寸驱动等功能通过改变图形的几何参数修改图形的形状，精确定位图形的大小，从而可以获得复杂的、精度高且满足不同设计要求的齿轮，对机械设计制造实践过程中高精度齿轮加工、轮系运动学和动力学分析及有限元分析都有着极其重要的意义。

1 基于SolidWorks的渐开线齿轮参数化建模流程

SolidWorks软件是美国SolidWorks公司开发的一款集二维设计、三维设计、有限元分析于一体的软件，是实行数字化设计的造型软件，在国际上得到了广泛的应用。SolidWorks软件具有开放的系统，添加各种插件后可实现产品的三维建模、装配校验、运动仿真、有限元分析、加工仿真、数控加工及加工工艺的制定，可保证产品在设计、工程分析、工艺分析、加工模拟、产品制造过程中数据的一致性，从而真正实现产品的数字化设计和制造，并大幅度提高产品的设计效率和质量[6]。本文借助SolidWorks的方程式功能模块探讨渐开线齿轮参数化精确建模设计，以提高齿轮建模效率，满足齿轮个性化设计需求。

借助SolidWorks软件实现渐开线齿轮参数化设计，就是设计者根据客户需求，结合实际设计提出的具体问题，在SolidWorks软件中预先设定齿轮参数约束，实现自动化设计齿轮的过程。渐开线齿轮参数化设计流程如图1所示。首先，对待解决的齿轮问题进行详细分析，并根据实际问题确定关键约束，即齿轮几何参数变量，且通过参数变量可以确定唯一模型；其次，借助SolidWorks的方程式功能模块构建变量方程式，构建渐开线阶段选定方程式中对应变量，完成渐开线设计；最后，观察绘制的齿轮模型是否符合要求，如果符合要求就保存输出设计模型，否则返回最初设计分析，重新分析设计需求以完成齿轮模型设计。

图1 渐开线齿轮参数化建模流程

2 渐开线齿轮精确建模

2.1 齿廓渐开线分析

齿轮精确建模的关键是构造轮齿渐开线，渐开线的极坐标方程为：

(1)

其中：rk为分度圆半径；rb为基圆半径；αk为渐开线压力角；θk为渐开线函数。

渐开线的形状取决于基圆的大小，基圆半径的方程为：

(2)

其中：m为齿轮模数；z为齿轮齿数；α为齿轮压力角，一般取20°。

基圆越大得到的渐开线越平直，当基圆半径无穷大时，渐开线成为一条直线[7]。

2.2 构造渐开线

本文以模数m为3 mm、齿数z为14的标准渐开线齿轮为例构造渐开线。

(1) 进入草图绘制界面，按公式(3)得到的尺寸绘制出分度圆、基圆、齿顶圆和齿根圆，如图2所示。

图2 分度圆、基圆、齿根圆、齿顶圆草图 图3 齿轮渐开线草图

(3)

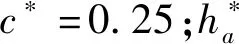
(2) 在“方程式驱动的曲线”中，选择“参数性”方程式，按照公式(4)分别输入Xt和Yt，用参变数t来形成曲线长度，可得到如图3所示的齿轮渐开线草图。

(4)

2.3 齿形构造与建模

绘制一条用于镜像渐开线的中心线，对图3中的齿轮渐开线使用“镜像”命令，使两条渐开线构成一个轮齿的两条边线，将分度圆上的齿厚S按式(5)定义，齿厚线与两侧渐开线定义重合约束，再修剪齿根圆与分度圆，绘制齿根圆角，并使所绘制的齿根圆角与基圆和齿根圆相切，齿根圆角的半径r见式(6)，至此完成了一个轮齿的绘制。之后对草图进行拉伸、阵列及键槽等命令操作，最终可以得到如图4所示的齿轮三维造型。

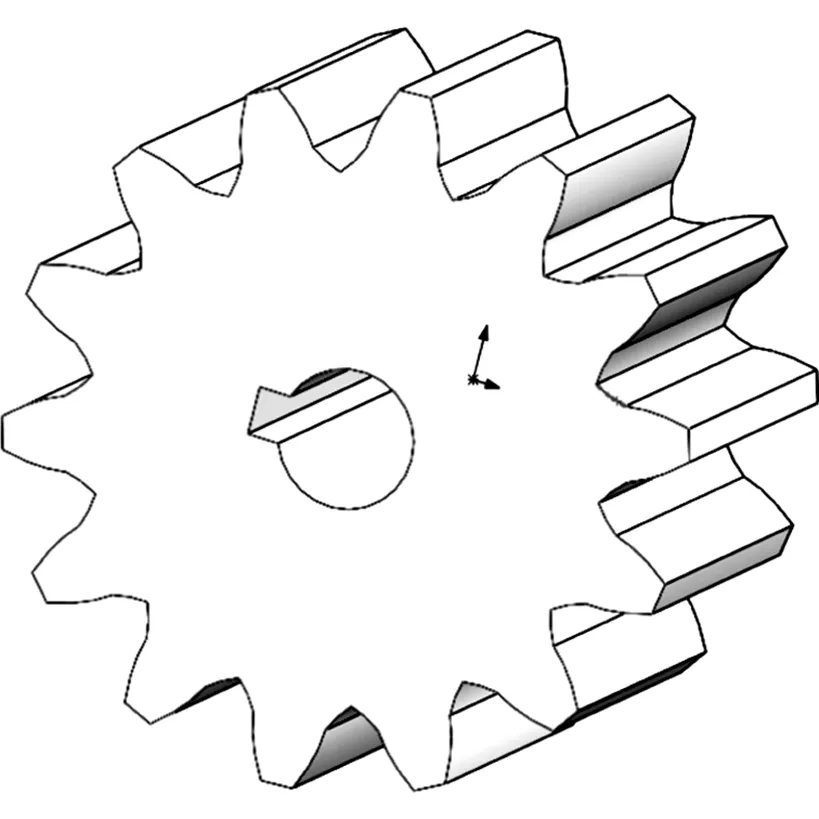
图4 齿轮三维造型

(5)

r=0.38m.

(6)

3 渐开线齿轮参数化建模实现

3.1 创建全局变量方程式

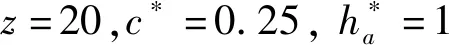
图5 ∑方程式界面

3.2 渐开线的构造

(1) 绘制齿根圆、基圆与分度圆。在草图中绘制齿根圆，尺寸标注输入选择全局变量，选择Df；绘制分度圆，尺寸标注输入选择全局变量，选择D；绘制基圆，尺寸标注输入选择全局变量，选择Db，为基圆半径尺寸添加方程式“D”*cos(20)/2。

(2) 绘制辅助中心线。以圆心O为起点绘制三条中心线，第一条竖直，与第二条中心线夹角添加方程式360/(“z”×4) 定义，第三条与第二条反方向定义20°。第二条中心线与分度圆交点为A，第三条中心线与基圆交点为B，以中心线连接点A与点B。

(3) 在基圆上做任意一点C，标注C点与B点的弧长即A点到B点距离。连接原点与C点，并做中心线与OC夹角为40°，与基圆交于D点。过D点做中心线DE与OD垂直，标注DE长度与CD弧长相等。通过约束关系做出渐开线齿廓上A点与E点的发生线。

(4) 得到一段渐开线齿廓。使用样条曲线工具，连接C、A、E三点，此曲线即为所求的渐开线，如图6所示。

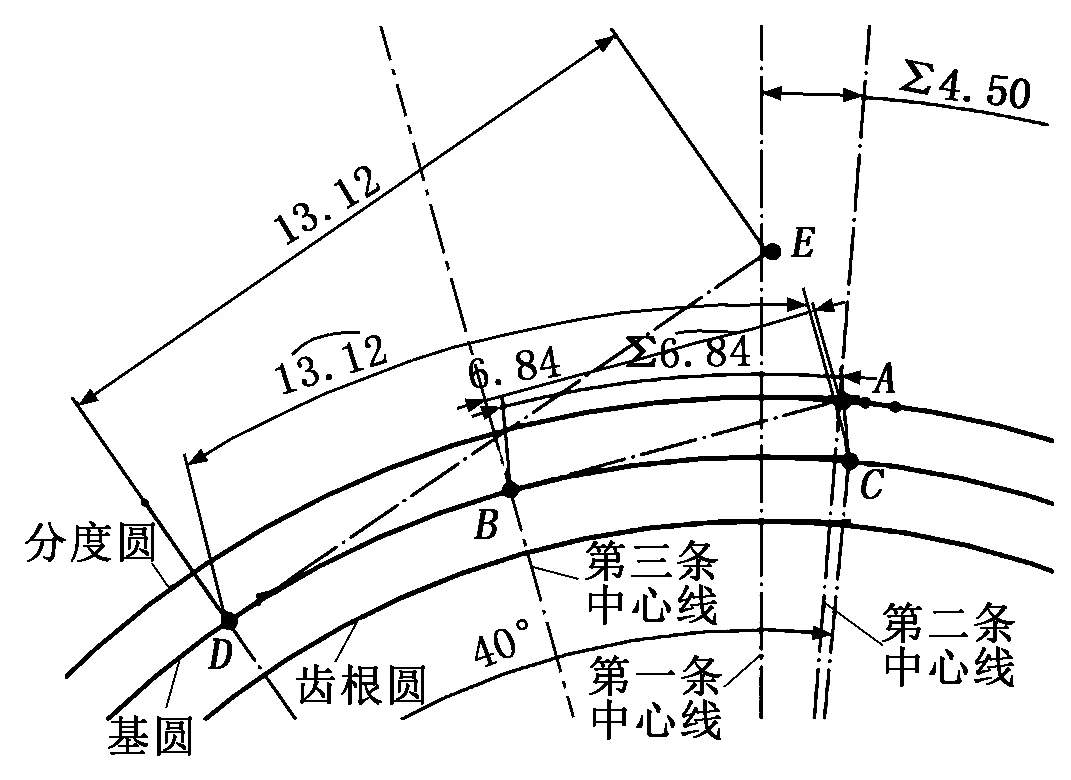
图6 齿根圆、分度圆和基圆草图

3.3 齿轮实体造型

以第一条中心线为轴，镜像渐开线和中心线OC，绘制齿顶圆，尺寸标注输入。裁剪后，拉伸轮齿厚度，阵列轮齿，数目选择全局变量z，绘制键槽拉伸切除即完成建模，如图7所示。

图7 参数化齿轮建模

4 结语

在保存以上文件后，只需改动模板方程式中的全局变量，即可得到不同齿数和模数的渐开线齿轮。此种方法基于齿轮参数公式与渐开线公式，同时结合软件方程式功能，保证了渐开线齿轮参数化精确建模，极大地提高了齿轮精确建模效率，同时也为其他零部件的参数化设计提供了设计方法和思路。