不同环境条件下的涡轴发动机性能参数换算方法研究
黄浩,黄向华
(南京航空航天大学 能源与动力学院,江苏 南京 210016)
0 引言
发动机在进行台架试车时,由于环境条件的影响,实测的发动机性能数据并不能反映发动机在标准条件下的真实性能[1]。为了使实测的性能参数方便与验收标准对比,更好地评估发动机性能,必须将实测的性能参数换算到标准大气条件下。
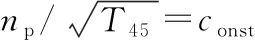
针对这一问题,KURZKE J[4]提出了一种基于模型的换算方法,利用高精度的发动机模型修正相似换算公式指数,提高了换算精度。黄开明等[5]提出了“等效相似换算”方法,先将自由涡轮恒定物理转速调节规律下获取的性能参数转化到自由涡轮恒定换算转速调节规律下,再进行相似换算。针对高空台模拟偏差,马前容等[6]提出用相似换算和小偏差分析相结合的修正方法。赵飞[7]分析了小偏差对性能参数的影响,提出一种线性矩阵修正方法。对传统相似换算的改进只考虑了环境温度和压力的影响,而小偏差分析方法只适用于小偏差情况。
1 修正系数法
本文参考涡喷、涡扇发动机采用的修正系数法,首先通过修正相似换算公式指数的方式修正只有环境温度和压力变化时涡轴发动机非相似工作条件的影响,然后以换算后的数据作为基数,乘以湿度修正系数完成对湿度影响的修正,修正后的换算性能参数为发动机在标准大气和干空气条件下的性能参数。
1.1 相似换算公式的指数修正
性能参数传统相似换算公式具有以下形式:
(1)
式中:X为试车实测得到的某个性能参数;XC为其修正之后的性能参数;θ=T0/T0,std,为温度换算因子;δ=P0/P0,std,为压力换算因子,其中T0,std和P0,std分别为标准大气温度和压力,下标“std”表示标准大气条件下的参数值,a和b为指数,分别反映了进口温度和压力对该性能参数的影响。
常用性能参数的指数a和b的理论值如表1所示,这是在发动机工作状态相似的情况下推导得到的。由于涡喷、涡扇发动机只能达到近似的相似工作状态,涡轴发动机工作状态的相似无法保证,因此a和b的值会不同程度地偏离理论值。如果能够得到与涡轴发动机相匹配的指数值,便可以实现涡轴发动机换算性能参数进口温度和压力的修正。

表1 常用性能参数传统相似换算公式指数理论值
由于大量的试验数据通常难以获得,因此通过在不同进口温度和压力下,运用修正过的高精度发动机模型获取与涡轴发动机更加匹配的指数值。下面以发动机换算燃油流量为例说明如何获得两个指数。
不同进口温度和压力下的燃油流量Wf可以通过换算公式换算到标准大气条件下的燃油流量,如式(2)所示。
(2)
可以得到燃油流量换算公式的指数为
(3)
计算指数a时,保持进口压力为标准大气压不变,使得δb=1,改变进口温度T0,可以计算得到不同进口温度对应的指数a,即aWf=f(T0)。
同理,对于δ的指数b,保持进口温度为标准大气温度不变,使θa=1,改变进口压力P0,得到bWf=f(P0)。
其他性能参数的指数计算过程与之类似。
1.2 获取某型涡轴发动机的指数a和b
建立某型涡轴发动机部件级模型,通过模型仿真数据计算出与之匹配的指数a和b。

计算θ的指数a时,在仿真过程中保持进口压力P0=101 325 Pa不变,将进口温度T0从238.15 K(-35 ℃)以5 K的步长逐步增加到313.15 K(40 ℃)。计算指数b时,保持进口温度为288.15 K不变,将进口压力从65 325 Pa以步长5 kPa逐步增加到120 325 Pa,出口背压与进口压力保持一致。
根据得到的仿真数据,采用式(3)计算得到新的指数a和b,分别如图1和图2所示。由于在仿真过程中保持恒定的ngc,使得压气机处于近似相似工作状态,所以压气机进口空气流量的指数与其理论值基本一致,其他参数的指数均不同程度偏离了理论值。

图1 基于仿真数据得到的指数a

图2 基于仿真数据得到的指数b
1.3 湿度修正
对实际涡轴发动机而言,性能参数不可能只受到当地大气温度和压力的影响,还受到大气湿度的影响。首先采用上文中得到的换算公式对实测得到的性能参数进行大气温度和压力的换算,以换算后的性能参数为基数,乘以湿度修正系数实现湿度修正。湿度修正系数定义为干空气条件下发动机换算参数值与湿空气条件下相应换算值的比值。如燃油流量湿度修正系数为
(4)
式中:下标“k”表示干空气;下标“h”表示湿空气。
最终考虑大气温度、压力和湿度影响的换算燃油流量计算公式为
(5)
本文采用含湿量d来描述空气湿度,定义为湿空气中水蒸汽的质量与干空气质量之比,单位为kg/kg。
保持进口压力和温度为标准大气压力和温度,仿真过程中将含湿量从d=0逐步增加到d=0.04,根据湿度修正系数的定义计算得到各个性能参数的湿度修正系数,如图3所示。可以看出湿度修正系数与含湿量呈线性变化规律,对其进行线性拟合,拟合得到的公式形式如下:

图3 湿度修正系数随含湿量的变化
CH=k·d+1
(6)
式中k为比例系数,值如表2中所示。表2中R2表示线性拟合的效果,R2非常接近于1,表明线性度很高,拟合效果很好,因此可采用线性拟合得到的公式计算湿度修正系数。

表2 线性拟合结果
1.4 修正系数法存在的问题
采用修正系数法时,湿度修正系数是在标准大气温度和压力下得到的,并没有考虑温度和压力的影响。图4和图5分别给出了不同温度和不同压力下的换算燃油流量湿度修正系数。从图中可以看出,温度和压力会对湿度修正系数产生影响。因此,当温度和压力不是标准大气温度和压力时,进行湿度修正时会产生一定的误差。要解决这个问题必须得到湿度修正系数与大气温度和压力之间的关系。然而由于其非线性的特点,这是难以获得的,因此需要找到一种新的性能参数换算方法。
2 基于神经网络的性能参数换算方法
由于涡轴发动机不满足相似工作条件,当环境条件变化较大时,性能参数的变化是非线性的,这是涡轴发动机性能参数换算的难点。神经网络为非线性系统提供了一种通用的系统辨识方法,能够以任意精度逼近任意非线性函数[8]。因此,针对修正系数法存在的问题,本文提出采用神经网络进行不同大气条件下的涡轴发动机性能参数换算。
2.1 原理
当涡轴发动机处于固定工作状态时(如额定状态),环境条件的改变将导致性能参数的改变。基于神经网络的性能参数换算方法将性能参数的变化看作是不同环境条件的非线性函数,函数关系式可以表示为
(7)
函数输入为环境条件,输出为性能参数相对于标准状态的变化量。
在不同环境条件下运行涡轴发动机模型,采用得到的仿真数据训练BP神经网络,拟合式(7)所示的非线性函数。在进行性能参数换算时,将当前大气条件输入训练BP神经网络得到的预测函数,便可得到当前大气条件下各个性能参数相对于标准状态下相应性能参数的变化量,由此得到换算之后的性能参数。
2.2 仿真验证
首先在不同进口大气温度、压力和湿度的组合下运行涡轴发动机模型,获得训练数据;然后采用Matlab工具箱完成神经网络的训练;最后随机选取50组大气温度、压力和湿度组合作为输入数据测试训练好的神经网络。同时在相同的大气条件下,采用相似换算和修正系数法进行性能参数换算,最终得到通过3种方法计算得到的换算性能参数。换算性能参数相对误差对比如图6所示,平均相对误差如表3所示。

图6 换算性能参数相对误差对比

表3 不同换算方法相对误差平均值 单位:%
可以看出,3种修正方法换算进口空气流量Wa2C的误差都很小,这是由于仿真过程中保持恒定ngc,使得压气机处于近似相似的工作状态。对于其他3个参数,修正系数法和基于神经网络的性能参数换算方法换算误差都远小于相似换算法。相比于修正系数法,基于神经网络的修正方法可以达到更高的换算精度。
3 结语
1)通过高精度的涡轴发动机模型仿真,计算得到最佳匹配的相似换算公式指数a和b,可以提高相似换算公式的准确性。
2)修正系数法在计算某个环境条件的修正系数时,并不考虑其他环境件的影响,这会导致一定的修正误差。
3)基于神经网络的性能参数换算方法优点有:计算过程更为简单且容易实现;考虑了多个环境条件的耦合影响;能够达到更高的换算精度。

