基于GASA-BRNN的齿槽转矩预测方法与分析

任鸿昌，王东瑞，姜添惠，张闯，陈文辉

(沈阳工程学院 ，辽宁 沈阳 110136)

0 引言

在永磁同步电机(PMSM)转动的过程中，由于电机齿槽与绕组分布不均匀，导致磁路不对称，定子与转子之间产生相对位移，使电枢齿槽与永磁体磁场间也产生相对位移，从而产生切向力，生成齿槽转矩，使电机产生振动和噪声，一定程度上降低其动态性能。目前国内外关于优化齿槽转矩方面的研究主要以有限元法、解析法分析齿槽转矩，对单一的结构参数进行优化，在离散的数据点中，寻找符合设计要求的值。此外还有部分学者，通过结合智能算法，构建多目标优化模型辅助电机设计，为多结构参数设计提出解决方案[1]。但是由于有限元法的计算时间长，解析法模型建立繁琐，程序实现困难且不同结构变量需要建立不同的解析模型。因此针对实际电机设计中要求的多目标、多结构参数优化设计，上述方法难以应对这种复杂非线性问题，为设计者形成一种快速参考方案。

本文首先在Rmxprt中建立一款永磁同步电机模型，选择3种结构参数为特征变量，齿槽转矩为输出，利用Ansys maxwell平台对 PMSM 进行有限元仿真实验，对选择的3种特征变量进行参数化计算，得到360组实验数据；然后设计一种基于GASA-BRNN神经网络算法的齿槽转矩分析模型，抽样300组作为训练输入，将剩余数据和利用Ansys Workbench中响应面实验(DOE)组件得到的13组数据混合作为测试数据，判断模型的泛化能力。最后通过对GASA-BRNN模型的预测结果与有限元计算结果对比，并将其性能指标与不同改进策略的神经网络模型进行分析，验证其预测精度与实际适用性。

1 永磁同步电机模型与齿槽转矩原理解析

1.1 电机有限元模型

本文将基于Rmxprt设计的一款4极24槽永磁同步电机作为典型研究案例，模型参数如表1所示。

表1 样机主要参数

通过在Ansys环境下Rmxprt与maxwell的快速对接，利用有限元仿真生成的PMSM二维模型如图1所示。

图1 PMSM仿真结构

1.2 齿槽转矩原理解析

空载运行下，定子和转子产生相对位移，导致其间隙发生变化，即气隙存在周期性变化，从而产生磁阻转矩纹波即齿槽转矩[2]，其可表现为断电情况下电机内存储的磁场能量对定子和转子相对位置角的负导数。

(1)

式中α为定子齿与永磁体中心线的夹角。若不考虑磁场饱和,电机磁场储存能量W可以近似看成电枢齿与永磁体之间气隙g中的能量，W可近似表示为电枢齿与永磁体之间气隙中的能量：

(2)

式中：μ0为空气的磁导率；V为气隙体积；B(θ,α)为磁感应强度，可近似表示为

(3)

式中：θ为永磁体沿圆周方向运动时与转子轴之间的夹角；hm(θ)为永磁体磁极厚度；Br(θ)为永磁体剩磁；δ(θ,α)为永磁体有效气隙长度沿圆周方向的分布系数。将式(3)带入式(2)，得到电机磁场储存能量：

(4)

假设发电机的每级磁通不变，令

(5)

(6)

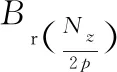
1.3 特征变量影响分析

在选择特征变量的过程中，应当选择对输出目标的影响具有明显特征的参数。本文选取极弧系数、永磁体偏心距、定子槽口宽度3种因子作为输入量，选取周期内电机空载转矩峰值为齿槽转矩输出量。通过有限元分析，分别计算在初始值条件下各变量与齿槽转矩的单变量变化关系，如图2-图4所示。

图2 极弧系数与齿槽转矩关系

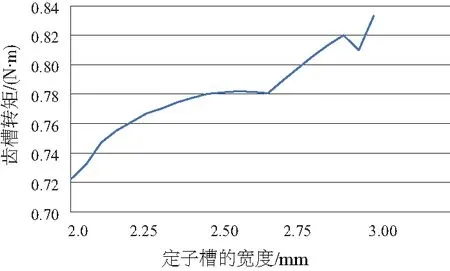
图3 定子槽口宽度与齿槽转矩关系

图4 永磁体偏心距与齿槽转矩关系

由有限元计算结果可知，在每种变量的变化范围内，均对齿槽转矩产生了明显影响，且影响趋势各不相同，变化曲线具有显著的非线性关系。

2 BP神经网络及其改进策略

2.1 BP神经网络原理

BP网络是一种典型的多层前馈型网络，广泛应用于模式识别、故障诊断，该模型结构如图5所示。

图5 三层BP网络结构

BP网络一般由输入层、隐藏层、输出层组成。数据从输入层依次传播至隐藏层、输出层，在输出层将误差反向传播并调整网络的权值参数，之后不断迭代上述步骤至误差为0，完成网络的训练过程。在误差反向传播过程中，令yk为第k个节点的实际输出，tk为其期望输出，误差函数为

(7)

(8)

式中：i、j、k分别表示输入层、隐藏层、输出层的神经元；p为输出变量数量；g(x)为激活函数；xi为输入量。

由式(8)可知，误差大小ED是权值wji、wkj的函数F(w)。因此通过调整权值来改变误差，使得三层及以上的网络结构能精准地描述出任意非线性关系，符合齿槽转矩分析模型要求。

2.2 贝叶斯正则化神经网络

标准BP神经网络在迭代中很容易陷入局部最小，而初始权值的随机确定导致每次拟合模型的精度差距过大，在针对复杂问题时的收敛速度过慢。目前广泛使用的Matlab神经网络工具箱默认的神经网络训练函数为Levenberg-Marquardt(L-M)算法，该算法多用于曲线拟合，在中小型网络中广泛应用，但是面对一个新输入样本具有很大依赖性。因此为提高齿槽转矩预测精度，提高模型泛化性，本文使用贝叶斯正则化(bayesian regularization，BR)算法来对神经网络进行改进。

神经网络中的贝叶斯正则化算法是一个根据L-M优化来更新权值和偏置值的网络训练算法，通过贝叶斯定理将平方误差和权重的组合最小化，确定正确的组合，从而产生一个泛化良好的网络[3]。

在贝叶斯神经网络中，定义网络的权值为随机变量，将网络权值和训练集的分布视为高斯分布，性能指数由式(8)转化为

F(w)=αEw+βED

(9)

式中：Ew是网络权重的平方和；指数参数α、β为贝叶斯网络中的优化参数。BP神经网络中寻得最小权值参数的目标函数是求式(8)的最小化，在BR神经网络(BRNN)中，寻得最小权重空间则需要将式(9)最小化，相当于求相对应的后验概率函数式(10)的最大化解集：

(10)

式中：w为权重分布；net为神经网络结构。解得F(w)在最小点wmin时α、β结果如下：

(11)

式中：λ为有效参数，λ=p-2αtrace-1(H*)，反映了构成模型的规模，其中H是F(w)在最佳拟合直线或平面上的投影矩阵(海森矩阵)。求解之后进入L-M算法流程，在文献[4]中有详细推导，本文不再赘述。BRNN将不必要的权重趋近0，有效地消除了网络的过拟合缺陷，同时使网络具有快速收敛的特性。

2.3 遗传算法

遗传算法GA是一种全局优化算法，利用遗传算法搜索BP神经网络的初始权重可以保证获得较高全局最优性的机会，因此，利用遗传算法可以有效抑制神经网络初始权值随机化的缺陷。为强化遗传算法的全局搜索能力，进一步降低算法陷入局部最优的可能性，本文将遗传算法与模拟退火算法SA相结合，提出了GASA-BRNN算法，设计流程如下所述。

1)将神经网络的权值和阈值编译成实数组作为遗传算法的染色体。初始化群体大小 30，交叉概率 0.3，变异概率 0.03，迭代次数50，退火温度1 000。

2)计算种群中个体的适应度，加入退火因子拉伸标准适应度

(12)

式中：Fn为第n个个体适应度；k为当前个体迭代数；t为温度。

3)按照遗传策略，对代种群进行选择操作、交叉操作和变异操作，形成下一代种群。结合 SA算法对产生的新种群采用Metropolis接受准则来确定，利用γn→m抽样其中的新个体m。

Metropolis准则公式如下：

(13)

式中：Δ为新旧染色体的适应度之差；tk为控制参数。

4)设置接受概率，采用轮盘赌方法，N为染色体数量，接受概率公式如下：

(14)

5)判断算法是否满足停止准则，如果不满足，则返回到2)；如果满足，则输出种群中最大适应度值的个体作为最优解，终止计算。

综上所述，运用GASA改进BRNN算法可以有效避免由于初始权重的随机确定而导致每次实验得到的模型精度存在较大偏差，并进一步缩小了算法陷入局部最优的可能性，流程如图6所示。

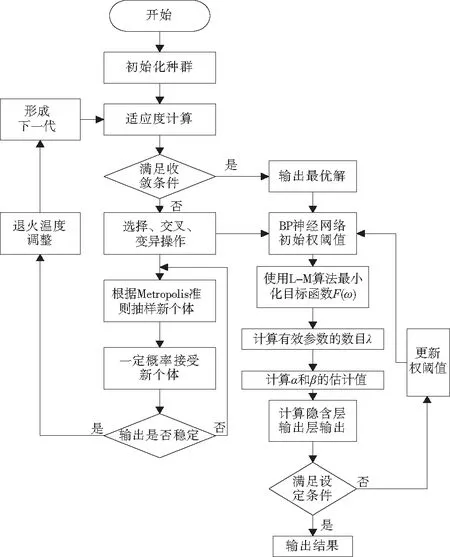
图6 GASA-BRNN流程结构

3 性能计算与对比验证

本文取极弧系数、定子槽宽度、永磁体偏心距作为特征变量，齿槽转矩作为输出，经全局计算得到输入、输出数据360组。为提高数据泛化能力通过中心化实验得到13组数据特征与全局计算不同的数据，将其与全局计算中的60组数据合并作为训练输入，用以评估建立的GASA-BRNN模型的准确性与对新数据的拟合能力。特征变量选取范围如表2所示。

表2 特征变量选取范围

3.1 初始化参数与算法实现

本文采用Matlab2019实现算法，通过确定神经网络层数与隐藏层节点数，选择激活函数与训练函数，添加学习率并给定网络的目标误差值，进行参数初始化调整，从而得到性能良好的网络模型。

在神经网络中输入层神经元数目h由输入数据的特征变量决定，输出层神经元数目l由输出变量决定，隐藏层神经元数目σ，一般选取经验公式如下：

(15)

式中：ξ为[0,10]之间的常数；本文样本空间中σ的取值范围在[2,12]之间。但是σ与其余参数的确定一般具有很强的经验规律，根据具体问题的表现也各不相同。因此通过选用均方误差MSE与绝对值误差MAE作为性能指标，对每次修改参数后的实验模型进行精度评估。MSE计算公式与式(7)相同，MAE公式如下：

(16)

式中：p为输出变量数，得到的值越小模型精度越高。多次实验后得到相对合理的网络参数配置如表3所示。

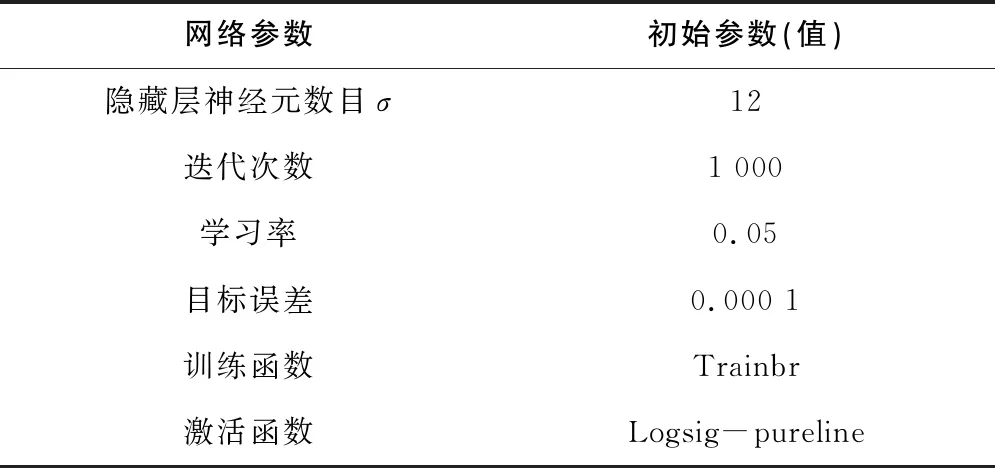
表3 网络参数配置

3.2 性能计算

由于激活函数特性，网络输出值均在[0,1]之间，同时由于有限元直接得到的数据具有一定序列特征，因此将数据导入模型前，需要对划分后的数据集进行归一化处理并进行随机排序再进行导入。在训练过程中，GASA算法调节适应度过程如图7所示。

图7 适应度调节过程

为直观显示GASA-BRNN模型在齿槽转矩预测方面的优越性，同时验证其在分析齿槽转矩中的可靠性，将模型得到的测试集数据与传统BP神经网络得到的测试集数据对有限元输出的实际值进行比较，可视化结果如图8-图9所示。

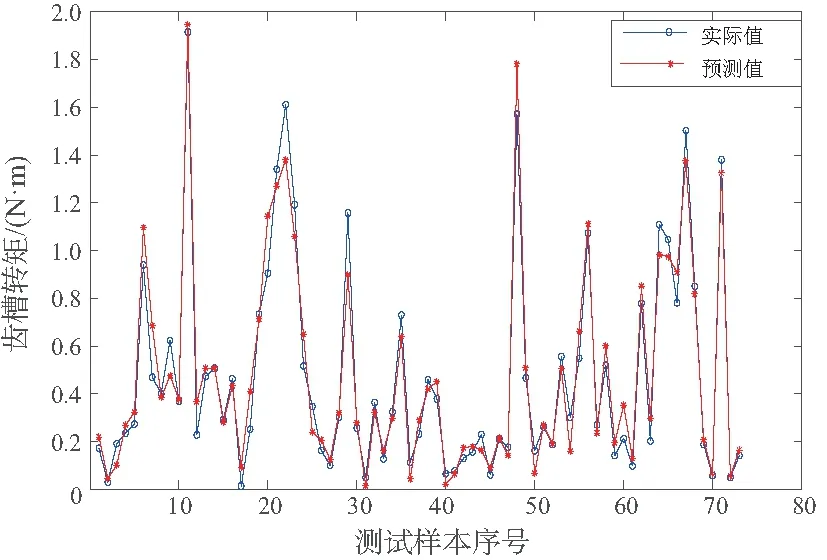
图8 BP神经网络预测结果

由图8-图9可以看出，本文提出的GASA-BRNN模型相比于标准BP神经网络具有更好的预测性能，对比有

图9 GASA-BRNN预测结果

限元方法得到的实际输出齿槽转矩曲线，GASA-BRNN模型具有令人满意的拟合程度。为进一步证明本文提出的模型在分析齿槽转矩方面的优秀性能，额外选取GA-BP、PSO-BP、RBF 3种神经网络模型，在训练调整各自最优初始值后，对测试数据的性能表现如表4所示。

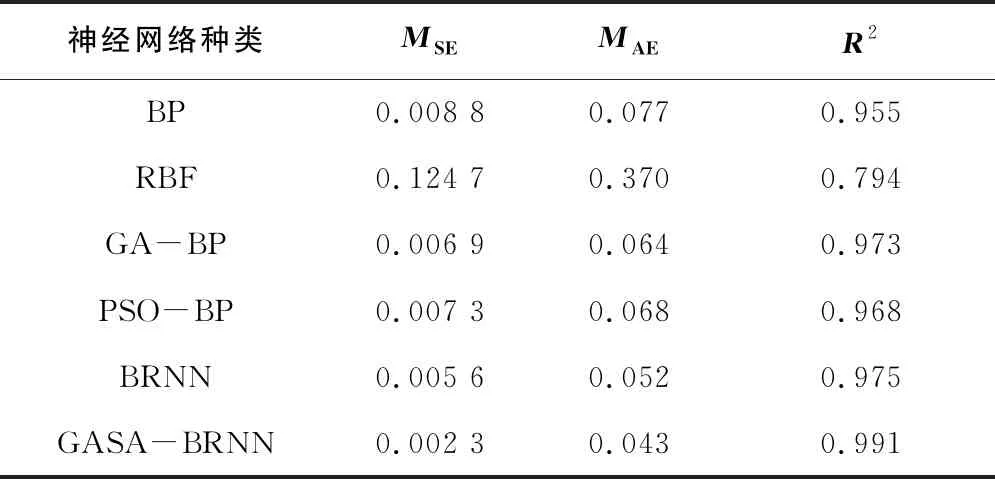
表4 性能表现

表4中R2为数据拟合的关联度，由性能参数可知，虽然各改进算法相对于标准BP各有提升，但是本文提出的以极弧系数、永磁体偏心距、定子槽口宽度为输入，齿槽转矩为输出的GASA-BRNN算法模型具有更加优秀的性能。

4 结语

本文将神经网络算法应用于永磁同步电机齿槽转矩的预测中，并根据BP神经网络的缺陷结合遗传算法与模拟退火算法进行改进，利用贝叶斯正则化训练算法提高了模型的泛化能力。在样本上则选择了三输入、单输出的PMSM小样本有限元仿真案例，通过数据处理反复进行性能分析实验，设计出良好的建模策略，完成了GASA-BRNN模型建立和对比分析，相对于文献[5]提出的深度学习模型， GASA-BRNN模型简化了实现过程，且根据各类性能指标以及与有限元计算结果的对比，显示其具有很高的预测精度，为电机结构实现快速设计奠定基础。