基于数据挖掘的汽车生产线螺栓打紧异常识别*

安 猛，孟新宇，陈长征，安文杰

(沈阳工业大学 机械工程学院，辽宁 沈阳 110027)

0 引言

在汽车零件装配过程中，螺栓联接是最基础、最广泛、标准化最高的连接方式。整车装配时，一辆汽车大概有4 000个～6 000个螺纹联接部件[1]，螺栓联接在汽车装配中发挥着重要的作用，有些甚至关系到人身安全。汽车生产线上关键部位最常使用的螺栓打紧方法为 “扭矩转角法”[2]，这种方法依据最终扭矩判断打紧是否合格，没有对过程数据进行分析，但过程数据往往反映打紧质量。螺栓打紧过程曲线发生较大变化时，虽然打紧结果能满足要求，但过程存在异常；出厂检验及用户使用时也证明打紧过程异常的螺栓多为不合格的故障螺栓[3]。本文主要对螺栓打紧过程进行研究，针对这种潜在的质量隐患，通过建立异常状态识别模型对其进行判别并及时做出提示。

实验数据为某一工位螺栓打紧数据集，打紧设备内有传感器，实时记录过程数据，主要包括过程的转角值和扭矩值、打紧时间等。对打紧样本数量统计，总样本为19 000条，正常样本为18 800条，异常样本为200条，仅占样本总体的1.05%，异常样本数量少且占比小，样本存在着类间不平衡问题。其中异常样本有两种：一种是打紧结果不合格样本，打紧设备可以识别；另一种是打紧结果合格，但过程异常，出厂检测时不符合要求，需要长时间反馈[4]。

1 数据处理

1.1 除噪

原始螺栓打紧过程数据如图1所示。原始数据易受到外界噪声干扰，导致类别间的特征显著性降低，影响特征提取[5]，过程数据在时间维度也有一定漂移，因此建模前需要对原始数据进行处理。

图1 原始螺栓打紧过程数据 图2 部分处理后的数据 图3 按固定角度切分扭矩

依据螺栓打紧工艺，清除停顿产生的噪声及打紧结束后引入的噪声。过程数据点计为{(Ai,Ti)∣i∈[1,n]}，表示第i个打紧过程，Ai为转角值，Ti为扭矩值，n为数据点的个数。依据打紧过程中噪声扭矩值远小于左右两侧扭矩的特点除噪，以i=1为起点，遍历数据集所有数据点。步骤如下：

(1) 差分计算每一个数据点，即Ti在i处一阶差分ΔTi为：

ΔTi=Ti+1-Ti.

(1)

(2) 当ΔTi<0时，把第i个数据点记作(Aflag,Tflag)，依据式(2)计算出ΔTflag，对满足ΔTflag≤0条件的(Ai,Ti)进行标记。

ΔTflag=Ti+1-Tflagi∈(flag,n).

(2)

(3) 当ΔTflag>0时，重复(2)、(3)步骤，直到遍历所有数据点并去掉标记数据。

当扭矩达到设定的最大值附近时，即视为打紧结束，记打紧结束点为(Af,Tf)，理想状态下结束点为(Ad,Td)，求得二者差值为S=Af-Ad，当S>0时，向左移动|S|个单位，当S<0时，向右移动|S|个单位。对所有过程样本进行此操作，完成主体数据集中。部分处理后的数据如图2所示。

1.2 特征提取

数据集直接特征为扭矩值[6]，打紧时扭矩有较大变化，对过程扭矩值特征进行提取。采集数据时，转动速度是变化的，不能利用采样点分割过程曲线，但转过的角度值A是固定的，现提出一种按角度值切分扭矩、提取特征的方法[7，8]。如图3所示，将过程曲线按一定角度切分，每个区域为一个目标窗口，计算窗口里扭矩平均值，将转角、扭矩转化为一定长度的扭矩向量[9]。第i条过程曲线扭矩向量Ti为：

Ti=[t1,t2,…,tA].

(3)

其中：tA为螺栓转动角度(A-1,A]中的扭矩均值。这样数据集由{(Ai,Ti)|i∈[0,n]}变为{Ti|i∈[0,A]}。在螺栓转动角度 [36°,58°]的范围内，以1°的间隔切分扭矩，可获取22个特征值。

2 模型算法

2.1 评价指标

在评价分类器性能时，基于混淆矩阵提出不平衡数据学习指标[10]。二分类中，分类结果为4种情况，如表1所示。

表1 二分类混淆矩阵

(1) ACC(分类精度)。ACC为分类正确的样本与分类器分类样本的比值，定义为：

(4)

(2) 特异性(Specificity)。特异性为分类器对少数样本的敏感程度，数值越大，对少数类样本分类性能越好，定义为：

(5)

(3) G-means。G-mean为多数类和少数类样本分类准确度的集合平均值，其可以合理评价整体分类性能，定义为：

(6)

(4) AUC面积(Area Under the Curve)。以FP/(FP+TN)为横坐标，TP/(TP+FN)为纵坐标，绘制ROC(Receiver Operating Characteristic)曲线[11]，中文名为“受试者工作特征曲线”，假设ROC曲线上有n个数据点，AUC定义为：

(7)

其中：x为TP/(TP+FN)；y为Specificity。 AUC值一般在[0.5,1]，数值越大说明分类器性能越好。

2.2 SMOTE改进算法

原SMOTE算法存在两方面问题[12-14]：合成的新样本只是来自两个少数样本对应的线段上，潜在出现范围仅在此线段上；在维度较高的特征空间中，对潜在少数样本的分布不足以完全描述。本文数据特征向量为22，维度较高，原SMOTE算法不再适用，需要改进。

改进思路是通过D个少数样本合成新样本，D是特征空间维数。首先，计算少数类样本k个同近邻样本，选取其中D个样本，以 0到1/D的权值对其矢量加和构建新样本。新样本空间从一维扩展到D维，下面是改进算法的具体流程。

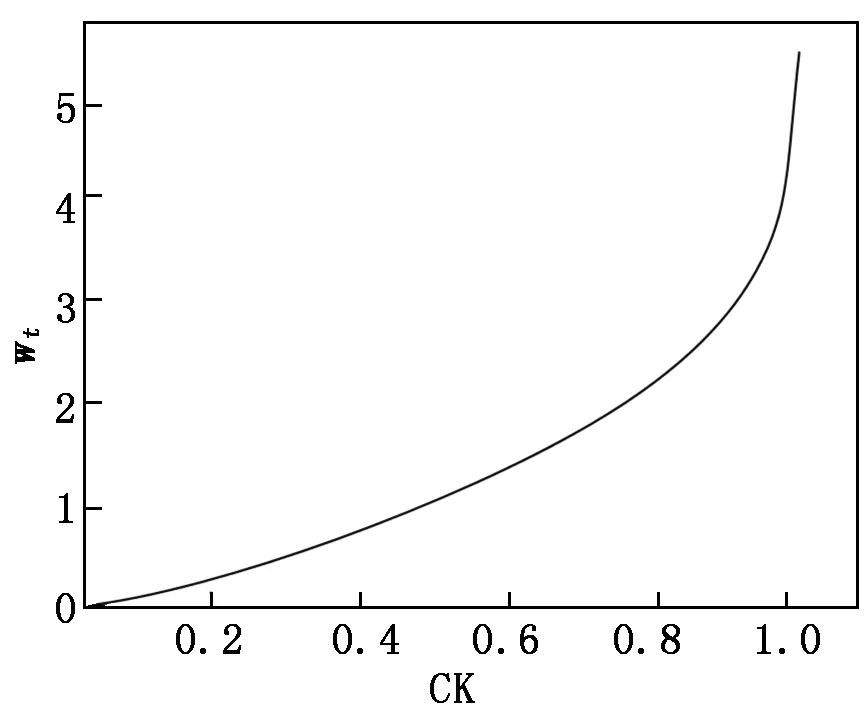
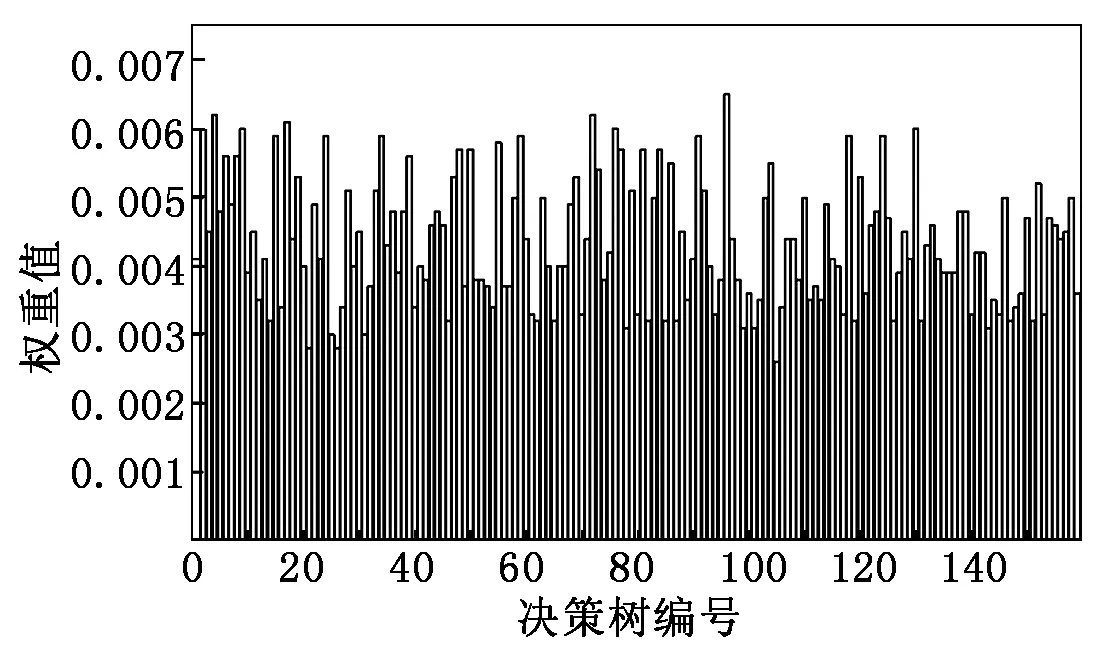
首先输入以下参数：P={P1,…,Pn}，为训练集中少数类样本集合；Pa为P中的一个样本；n为少数类样本个数。设k为近邻个数；D为参与合成新样本的近邻个数,D

接着，完成以下算法：

(1) 利用集合P构建Kd树；

(2) fori=1 tondo；

(3) 通过Kd树找出Pi的k近邻：Kni={kni1,kni2,…,knik}；

(4) fora=1 toNdo；

(5) 在Kni中随机选取D个近邻样本：Kn′a={kn′a1,kn′a2,…,kn′aD}；

(6) 在[0,1/D]中随机选取D个实数(能够重复)：da={da1,da2,…,daD}；

(7) 计算被选取的近邻样本和Pa的向量差：vecan=kn′an-Pa；

(9) 新样本加入集合：newa→Samples；

(10) End for。

最后输出：新样本集Samples。

如图4所示，P点为合成新样本的目标样本点，A和B为两个同类近邻样本点，C和D为合成样本点。图4(b)中，A、B样本点的合成权值为dA、dB，取值范围(0,0.5]，特征向量P′=P+dA(A-P)+dB(B-P)。平行四边形边长分别为0.5PA与0.5PB，合成的新样本C、D位置范围在平行四边形内。而在图4(a)中，原算法生成的样本点C、D在PA和PB线段间。

图4 算法改进前、后对比图

2.3 加权随机森林算法

一个已训练完的随机森林模型[15-17]决策树数量为T，测试集为X，类别数为C，模型输出为：

(8)

其中：ht(X)为第t棵决策树的输出；I(·)为一个指示函数。

由式(8)可知，每棵决策树投票权重都为1，但各决策树的分类准确度不同[18]。对此本文提出了加权随机森林模型，即在训练时评估出每棵决策树的分类性能，并根据性能赋予对应权重，在投票时，乘上对应的权重值，能够降低训练精度不高的决策树对整个模型的影响。因此，公式(8)可改写为:

(9)

其中：wt为第t棵决策树的权重值。

利用袋外样本[19]作为每棵决策树的测试集来评估分类性能，并据此结果赋予相应权重，使性能好的决策树拥有更重要的位置。

使用Kappa系数(CK)评价决策树整体分类性能，CK是评价一致性程度的指标，能够考虑到各种漏分与错分样本，能表示分类与随机分类错误减少的比例。一般情况下CK为(0,1)，CK值越大，说明结果与实际结果越一致，分类器性能越好[20]。CK由下式计算：

(10)

其中：CKc为分类的偶然一致性比率，计算公式如下：

CKc=

(11)

为了把较大的权重分配给性能更优的分类器，文献[21]指出：一组相互独立的分类器L1,L2,…,LM，准确度为p1，p2，…,pM,各分类器的权重与相应准确度关系如式(12)所示：

(12)

将式(12)中的p替换成CK，其中CK的取值范围为(-1,1)，公式(12)可改写为：

(13)

依据公式(13)，决策树的CK值越大，其分配到的权重也越大，对最终投票结果影响也越大。CK与wt的关系如图5所示。可将式(13)代入式(9)，从而得到最终的输出结果。加权随机森林算法流程如图6所示，根据得到的CK值决定每棵树的投票权重，降低分类性能差的决策树对最终结果的影响，输出的结果更合理，也能够提高整体的分类性能。

图5 CK与wt的关系

图6 加权随机森林算法流程

3 建立模型并验证

3.1 算法对比结果

本文算法均使用Python语言编写，在Jupyter notebook平台上调试并测试。为验证改进的SMOTE和加权随机森林算法对螺栓打紧数据集分类效果的影响，将SMOTE(SM)、改进SMOTE(ISM))、随机森林(RF)、加权随机森林(WRF)，根据不同的组合形成不同算法模型，即SM+RF、ISM+RF、SM+WRF与本文的ISM+WRF模型。在经处理后的打紧数据集上，实验这4种算法，并对得到的结果进行比较。

根据不同算法建立模型并训练、测试，结果如表2所示，ISM、WRF与SM、RF相比，都能提高分类结果的Specificity，表明经过改进的算法都能提高少数类样本的分类准确性。从SM+RF和SM+WRF的对比结果看出，数据集的G-mean、CK和AUC均有提升，与未改进的SM+RF算法相比，SM+WRF算法的G-mean提升了3.6%,CK提升了8.23%，AUC提升了3.8%，说明加权随机森林比传统随机森林的分类性能更好。从SM+RF和ISM+RF的对比结果也可看出，ISM对数据集的分类效果也有提升，各指标均提高3%以上，也说明改进的SMOTE算法比原算法的分类性能更好。从数据层面改进的ISM与从算法层面改进的WRF对分类效果均有提升，结合ISM和WRF的算法模型对不平衡数据集的少数类及整体分类效果最好，在螺栓打紧数据集非常适用。

表2 不同算法与本文算法分类结果对比

对ISM+WRF模型调参至最优，获得159棵决策树并求得各决策树权重值，如图7所示，数值范围在[0.002,0.007]。不同的决策树分类性能不一致，对随机森林的贡献不同，权重值也不同。绘制参数调优后模型的学习曲线，如图8所示，当数据增加时，训练集分类准确性曲线(虚线)和测试集预测准确性曲线(直线)靠的较近但有一定距离，并随数据增加相持平，最后收敛于0.998以上，说明模型不过拟合也不欠拟合，效果较好。

图7 加权随机森林决策树权重值

图8 随机森林模型学习曲线

3.2 实验验证

对螺栓异常状态识别模型进行实验验证，在打紧数据库提取600条样本，其中正常样本521条，异常样本79条，输入到模型中得出识别后的结果，如图9所示。由图9可知，所有打紧正常螺栓及74条打紧异常螺栓被正确识别，仅5条打紧异常螺栓被误分到正常类中，对打紧异常螺栓识别率达93%以上，说明模型识别打紧异常螺栓效果较好。

图9 测试效果

4 结论

汽车生产线上螺栓打紧设备的打紧结果只通过最终扭矩值判断，缺乏对过程数据分析，会漏掉少量打紧异常螺栓。出厂检测时，发现异常螺栓，多为不合格螺栓,需重新打紧，影响生产效率，增加生产时间和成本。同时，打紧质量在检测和初期使用中也难以评估，本文提出的螺栓打紧异常状态识别模型是针对过程，能够有效识别异常螺栓，并及时采取措施。在后期研究中，探索打紧过程与打紧质量的关系将成为分析螺栓联接质量的一种新途径。