高要地区不同重现期风速风压的估算
赖亚胜
(肇庆市气象局,广东肇庆 526040)
重现期风速、风压是建设项目的安全设计和造价的重要参数。因此开展大风变化以及基本设计风速风压研究是风电开发、桥梁道路设计、港口码头、高层建筑布局等工程气象应用中不可缺少的重要内容,也是经济发展及资源环境保护的迫切需要[1]。很多学者在极值风速计算和风速的垂直分布特征等方面取得一定研究成果。如史军等[2]结合皮尔逊Ⅲ型和极值Ⅰ型概率分布两种拟合方法,推算出上海不同重现期最大风速值;马玉峰等[3]基于极值Ⅰ型概率分布模型,分析得出内蒙古东部极值风速重现期分布图;代玉伟等[4]通过对历年最大风速值统计论证,得出了白城地区建设输电线路应采用的基本设计风速值;张庆等[5]利用梯度风速观测数据,通过案例分析了台风过程中深圳近地面水平阵风因子的垂直分布特征。上述研究表明,极值Ⅰ型是拟合我国各气候区最大风速模式中最理想的方法。
肇庆市高要区位于广东省中部,西江中下游,属南亚热带季风气候区,每年夏季的台风、雷暴大风以及冷空气大风常引发灾害[6]。本研究利用历史风速序列重构和极值风速分布等方法,将收集到的高要地区历年最大风速值进行统计和分析论证,估算高要不同重现期风速的变化,以期为高要大型工程项目抗风设计和城市建设规划提供参考。
1 资料和方法
1.1 数据资料
本研究站点资料为高要国家地面气象观测站(以下简称高要站)1991—2020年风速和风向观测资料。高要站位于广东省高要区莲塘镇上察村波西岗东岗,海拔高度40.1 m。
1.2 重现期最大风速计算
最大风速重现期估算需判定其理论频率是否满足某个概率分布模型[7]。风速极值的重现期计算一般有4种方法:Gumbel分布(极值Ⅰ型分布)、Weibull分布和皮尔逊Ⅲ型分布、对数正态分布[8]。经大量实例验证后发现,对于较小概率的风速极值,Gumbel分布的拟合效果较理想,误差最小,《建筑结构荷载规范》(GB50009-2012)[9]也推荐使用该方法。
Gumbel分布的分布函数由下式表达:
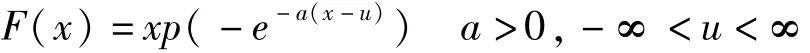
其超过保证率函数为

超过保证率P对应的重现期风速为

参数a及u的估计一般用Gumbel法:
假定最大风速有序列:x1≤x2≤……≤xn,则经验分布函数为

取如下序列:

可得:
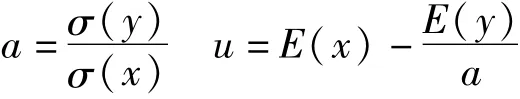
其中,σ(x)和σ(y)分别为序列xi和yi的均方差;E(x)和E(y)分别为序列xi和yi的数学期望,在实际计算中可用有限样本容量的均值和标准差作为E(x)和σ(x)的估计值。
1.3 基本风压的计算
工程结构设计中,一般用风压表示风力作用的大小[6]。按贝努利公式,根据风速可求得相应的风压值为

其中,w为风压(kN/m2);v为重现期风速(m/s);ρ为当地的空气质点的密度(t/m3),若空气密度可采用高要站历年气象资料进行推算,计算公式为

其中,T、P分别为高要站的平均气温(K)、平均气压(Pa);R为气体常数(287 J/(kg·K))。空气密度向不同高度推算采用如下公式:

其中,ρz为海拔高度为z处的空气密度(t/m3);ρh为温度、气压传感器安装高度处(海拔高度为h)的空气密度(t/m3)。
2 大风统计
统计可知,1991—2020年高要站各月6级以上大风日数共有93 d,主要出现在5—9月,占总大风日数的88.2%。6级以上大风风向频率最大的为东北偏东风,频数为23.2%,其次为东北风和东北偏北风(图略),这表明1991—2020年该区域的大风主导风向为东北偏东风,其次为东北风。
3 高要地区基本设计风速推算
3.1 高要站年最大风速序列订正
1)时距订正。
按相关规范要求,年最大风速时距为10 min,高要站1991—2020年时段内的最大风速为逐时观测的10 min平均年最大风速,故在此无需进行风速时距(2到10 min)的订正[10]。
2)高度订正。
根据高要站测风历史沿革,其测风仪设置高度设计时已充分考虑观测环境状况,可代表10 m高度风速,无需进行高度订正。
3)一致性订正。
高要站1991至2020年期间分别于1998年8月1日和2016年1月1日进行过两次搬迁。采用t检 验 对 1991—1997 和 1998—2015、2016—2020年3段数据进行差异的显著性检验。
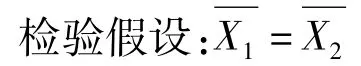

其中分别为1991—1997和1998—2015年两段年最大风速序列的平均值,其比值分别为对应的样本数;S1=1.85 m/s、S2=4.14 m/s分别为对应的风速均方差。|t|=1.87<t0.05=2.74,原假设成立,说明在给定信度α=0.05条件下,迁站前后的年最大风速序列无显著差异,无需订正。分别为1991—1997和2016—2020年年最大风速序列平均值,其比值,经检验|t|=2.64>t0.05=2.57,原假设不成立,说明在给定信度α=0.05条件下,迁站前后的年最大风速序列存在显著差异,需采用比值法订正,1991—1997年最大风速乘以订正系数1.594。
经上述订正,得到高要站30年完整的距地面10 m高度上10 min年平均最大风速,符合相关规范的要求,可用于基本风速的概率推算。经过上述3个订正步骤,建立10 min平均年最大风速序列(图略),可以看到,最大值为27.3 m/s,出现在2018年;最小值为10.2 m/s,出现在1998年。
3.2 高要地区设计风速的估算
1)各重现期最大风速计算结果。
利用高要站1991—2020年距地面10 m高度10 min平均年最大风速序列,对高要地区不同重现期最大风速时间变化的估算。采用Gumbel概率分布函数(极值Ⅰ型分布)进行参数估计,得出高要地区不同重现期最大风速随时间变化满足极值Ⅰ型概率分布模型(图1)。

图1 高要国家气象站设计风速极值Ⅰ型概率分布曲线拟合图
根据Gumbel概率分布函数推算地面10 m高度各重现期风速结果见表1。
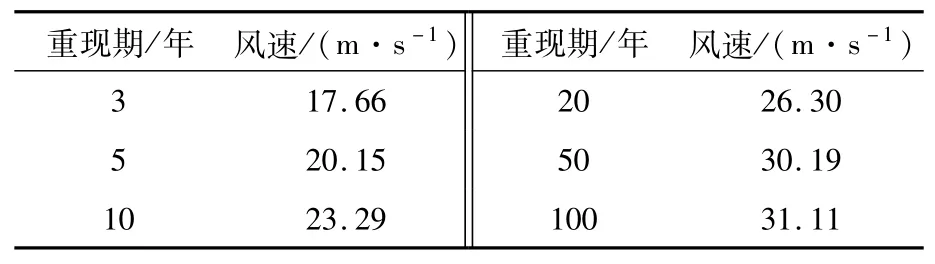
表1 高要国家气象站10 m高度各重现期10 min平均风速
2)风速随高度变化的推算。
相同条件下,离地面越近风能量受阻力越大,相应的离地越高阻力越小,因此风速和海拔高度呈正相关关系。近地层风的垂直分布主要取决于地表粗糙度和低层大气的层结状态[11]。对数和幂指数方程都可以较好地描述风速的垂直廓线,新修订的《建筑结构荷载规范》也推荐使用幂指数公式,其表达式为其中,v2为高度Z2处的风速(m/s);v1为高度Z1处的风速(m/s);α为风速垂直切变指数,为量纲一的数,其值的大小即表明了风速垂直切变的强度。

计算高要地区的工程厂址不同高度层重现期风速时,应先确定其地表情况,通过风速地表修正系数(参照表2)换算10 m高度重现期风速,然后再根据相应的风切变指数,按照幂指数公式推算不同高度层的重现期风速。

表2 各类地表对应的风切变指数和地表修正系数
以B类地表为例,推算高要地区各高度各重现期10 min平均风速,见表3。

表3 高要地区各高度各重现期10 min平均风速 m/s
3.3 极大风速
工程计算中通常采用阵风系数将重现期10 min平均风速换算为极大风速(3 s阵风),由于本项目没有实测的阵风系数,参照《建筑结构荷载规范》统一取1.30,由重现期10 min平均风速推算对应的极大风速,结果见表4。

表4 滑雪场各高度各重现期3 s极大风速 m/s
4 最大风速风压特征
根据10 min设计风速及相应空气密度,以B类地表(α=0.15)为例,计算高要区设计风压,结果如表5所示,10、30、50和100年重现期的设计风压分别为0.32、0.54和0.65 kN/m2,高于《建筑结构荷载规范(GB5009-2012)》中的参考值(0.30、0.50和0.60 kN/m2),说明该风压参数作为高要地区抗风设计重要参考是合理、可靠的[12]。

表5 高要地区各高度各重现期风压 kN/m2
5 结论
1)高要站近30年年均大风日数为93 d,主要出现在5—9月,主导风向为东北偏东风。
2)极值风速的空间分布情况受高度和地形、下垫面等因素的影响。1991—2020年期间高要地区10 m高度10、50和100年重现期的最大风速分别是23.29、30.19和31.11 m/s。
3)1991—2020年期间10 m高度10、30、50和100年重现期的极大风速分别为30.3、39.3和43.0 m/s。
4)以B类地表(α=0.15)为例,推算高要地区各高度各重现期最大风速和基本风压,其结果高于《建筑结构荷载规范(GB5009-2012)》中的参考值,作为高要地区抗风设计参考合理可靠。

