多气室薄膜充气管结构特性研究★
高海健,赵苏宁,孙 进,杨 峰
(1.南通理工学院,江苏 南通 226002; 2.南京思成建筑设计咨询有限公司,江苏 南京 210014)
充气膜结构具有自重轻、强度高、可折叠、快速安装等特征,因而广泛应用于建筑、航空航天、应急救援等领域,如建筑场馆、大型可展天线、浮空器、可充气式太空舱等,特别是在疫情期间,一批充气式实验舱、防疫设施快速地建设并投入使用,在疫情防控工作中发挥了重要的作用。而薄膜充气管是一种最基本的充气膜结构,很多复杂充气膜结构以充气管为基本受力构件,对其结构特性研究具有重要意义和价值。国内外对充气管已进行了一系列较为深入的研究。文献[1]推导了充气悬臂梁挠曲线微分方程; 文献[2]采用线弹性理论对充气管进行分析,利用最小势能原理计算了充气管的屈曲荷载;文献[3]进行了充气梁试验,并与工程弹性理论计算结果比较,验证了工程弹性理论的适用性; 文献[4-5]推导了基于铁木辛柯梁理论的挠曲线微分方程,得到高压充气管的荷载与挠度关系。近年来,国内对充气梁的研究发展较快,文献[6]研究了薄膜充气管在承载过程中的屈曲行为,利用梁单元进行充气管承载特性的有限元数值分析;文献[7]考虑压力追随效应修正,推导了充气悬臂梁挠度计算方程,并进行理论计算和实验结果的对比分析;文献[8-10]对薄膜材料力学性能进行试验研究,利用试验结果为参数,通过多种数值计算模型对薄膜充气管受力特性进行模拟计算,考察计算模型的适用性;文献[11]研究了充气梁在弯曲荷载作用下的整体-局部耦合失稳行为,得到了充气压力与结构尺寸对充气梁屈曲行为的影响规律。这些研究都基于单气室充气管,目前对多气室薄膜充气管结构性能的研究还不多,本文采用有限元数值模拟计算方法,建立多气室薄膜充气管模型,通过管径、端部载荷等多种参数分析,得到多气室薄膜充气管的受力特性与变化规律,为新型薄膜充气结构的设计应用提供依据。
1 单气室薄膜充气管结构特性
1.1 工程弹性理论
根据薄膜充气管工程弹性理论(Euler-Bernoulli 梁理论[1]) ,充气管环向和纵向张力表达式分别为:

其中,f1为薄膜充气管环向张力;f2为薄膜充气管纵向张力;p为管内气压;r为充气管半径。
当在梁端施加作用力F后,悬臂充气管理论分析模型如图1 所示,假设应力沿充气管截面线性分布,将膜内张力换算成膜内应力,则充气管环向应力不变,纵向应力随截面弯矩变化,在受压侧应力最小。
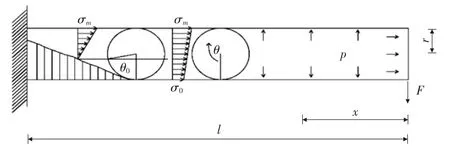
图1 悬臂充气管分析模型
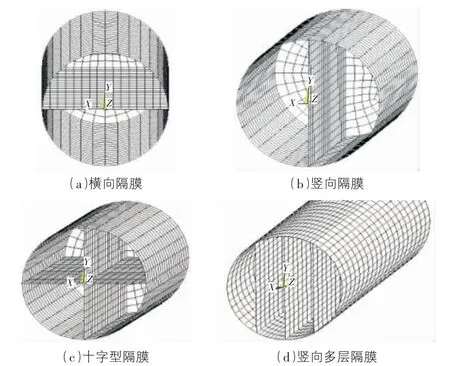
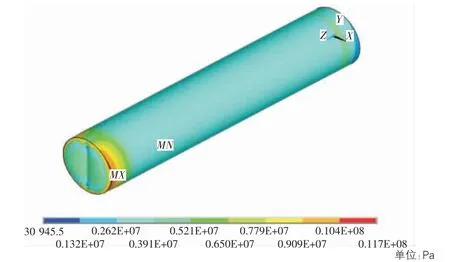
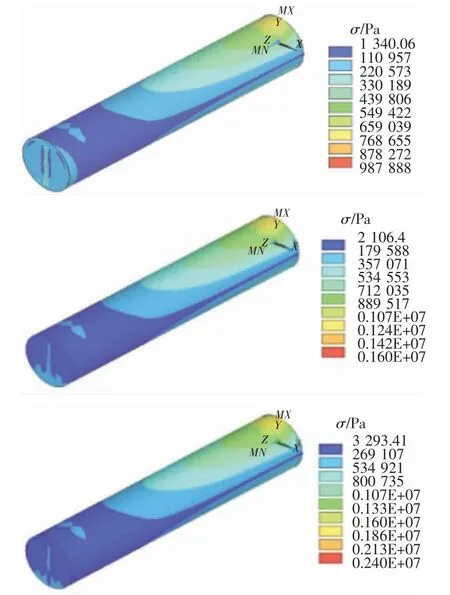
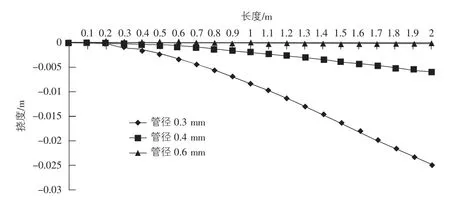
当0 当πpr3/2F 其中,σm为薄膜充气管受拉侧最大应力;σ0为薄膜充气管受压侧最小应力;θ为充气管截面内从σ0位置处起算的夹角;θ0为充气管截面内从σ0位置处起算的褶皱区域夹角。 考虑薄膜充气管未产生褶皱,其挠度方程可表示为: 其中,E为薄膜材料弹性模量;I为薄膜充气管截面惯性矩,I=πtr3;l为薄膜充气管长度。 由式(1) ,式(2) 和式(6) 可知,薄膜充气梁环向张力和纵向张力与管内充气压力成正比,而挠度则与管内充气压力无关,仅决定于截面几何刚度,与外力成线性关系。 由于薄膜充气管工程弹性理论计算式有许多限制条件,其挠度计算不能考虑气压对挠度的影响。因此,工程弹性理论计算结果一般适用于薄膜充气管总体受力和变形计算,可在初步设计中进行初步受力评估。实际上,膜材本身的弯曲刚度几乎为零,但通过不同的支撑体系使薄膜承受张力,从而形成具有一定刚度的稳定曲面,力的平衡状态直接被表现在结构的形状上,薄膜充气管正是通过管内充气压力产生抗弯刚度。为更好地认识薄膜充气管受力机制,以及荷载作用下膜内应力分布及变形特征,本文采用非线性有限元法对薄膜充气管进行数值计算分析,利用通用有限元软件ANSYS 建立模型,考虑到膜结构的变形一般较大,其变形对结构自身尺度和位形的影响不能忽略,表现为大变形、小应变特征,所以采用薄壳单元模拟膜面,考虑结构大变形效应的影响,进行模拟计算,把气压和其他受力都作为荷载同时施加。主要步骤为:1) 建立几何模型;2) 有限元网格划分,单元类型选用三角形或四边形等参壳单元;3) 赋予真实材料参数;4) 定义边界条件,本文根据研究需要主要对悬臂薄膜充气管进行计算;5) 施加外荷载(气压及集中荷载,考虑到集中力对薄膜局部结构特性影响较大,故管端集中荷载一般以集中荷载方式均匀作用于薄膜充气管整个截面所有节点进行有限元计算) ,并进行荷载分析。 有限元模型如图2 所示,薄膜充气管一端固定,一端自由,长度l=2 000 mm,充气管半径r=200 mm。膜材弹性模量E=7.063 9×108Pa,泊松比μ=0.38,膜材厚度t=0.482 mm。采用Shell63 四边形平面应力单元划分网格。 图2 单气室薄膜充气管有限元模型 假设薄膜充气管内气压P=400 Pa,取薄膜充气管距管端1 000 mm 处截面上侧节点,有限元计算得到该处环向、纵向应力的计算值与理论值对比见表1。 表1 气压作用下应力理论值与计算值对比 由有限元计算结果与理论计算结果比较可得,有限元计算值比理论计算值稍小,两者非常接近,数值计算得到环向应力与纵向应力之比为1.98∶1,表明有限元计算方法能够有效模拟薄膜充气管的受力性能。 当梁端作用力F=48 N,管内气压p=10 kPa,单气室薄膜充气管有限元计算Mises 应力云图如图3 所示,由计算结果可知,薄膜应力随气压增大而增大,梁端荷载产生的弯矩使约束端上部应力增大,下部应力减少并出现最小应力值。薄膜充气管侧边线端部挠度为v=16.3 mm,而由式(6) 理论计算端部挠度为v=14.9 mm,数值计算挠度比理论计算挠度稍大,两者比值约为1.09∶1,且数值计算结果能反映气压对挠度的影响。由上可知,数值计算方法能较好模拟薄膜充气管应力、变形及各种因素对其影响。 图3 单气室管端部荷载作用下应力云图 实际工程中,充气膜结构内部一般都设置若干隔膜以满足结构受力及功能需要,为便于研究多气室薄膜充气管的基本受力性能,进一步了解掌握薄膜充气管受力、变形等变化特征,本文在单气室薄膜充气管数值分析研究基础上,通过模型简化,在单气室薄膜充气管内增设竖向或横向隔膜,构成多气室薄膜充气管,其几何尺寸和材料参数同上文,多气室薄膜充气管有限元模型如图4 所示。 图4 多气室薄膜充气管有限元模型 先对多气室薄膜充气管在梁端荷载作用下的力学性能进行研究,在薄膜充气管中间设置竖向隔膜,构成左右相同的两气室薄膜充气管,管内气压为p=10 kPa,当梁端作用垂直向下的荷载F=48 N,数值计算得到多气室薄膜充气管应力云图如图5 所示,薄膜充气管侧边线端点处的应力和挠度,与上文单气室薄膜充气管数值计算结果进行比较,见表2。 图5 多气室管端部荷载作用下应力云图 表2 单气室与多气室薄膜充气管应力及挠度对比 计算结果表明,与相同条件下单气室薄膜充气管相比,多气室薄膜充气管应力分布以竖向隔膜为中线呈对称分布,侧边线端点处应力和挠度均有降低,竖向隔膜与管壁的交线处应力和挠度降低尤为明显,表明竖向隔膜的作用比较显著,能够增加薄膜充气梁的整体抗弯刚度,对隔膜连接处局部管壁膜内应力改变较大,提高了其抵抗面外变形的能力。下面,进一步对多气室薄膜充气管应力及挠度的影响因素进行讨论研究。 以中间设置竖向隔膜的薄膜充气管为例,管内气压为80 Pa,距固定端1 800 mm 处作用垂直向下的荷载,当荷载值F分别为160 N,320 N,400 N 时,数值计算应力云图如图6 所示。 图6 悬臂薄膜充气管不同端部荷载作用下应力云图 计算结果表明,在端部荷载作用下,悬臂薄膜充气管薄膜最大应力随梁端荷载增大而增大,应力最大值一般位于靠近固定端上部管壁处;同样,挠度也与梁端荷载有关,随荷载增大挠度越大,具有较明显的非线性特征,不同端部荷载作用下,薄膜充气管管壁侧边线挠度变化见图7。 图7 悬臂薄膜充气管挠度与荷载关系 隔膜如何设置对薄膜充气管受力性能也有比较大的影响,在薄膜充气管中间分别设置横向隔膜(gm1) 、竖向隔膜(gm2) 、竖向多层隔膜(gm3) 构成多气室薄膜充气管,管内气压为80 Pa,在悬臂端部平面内左侧、右侧、下端三处节点分别作用垂直向下的荷载F=100 N,数值计算可得薄膜充气管管壁侧边线挠度见图8。 图8 隔膜构型对悬臂薄膜充气管挠度影响 计算结果表明,改变隔膜布置位置能够改变薄膜充气管的抗弯刚度,横向隔膜对薄膜充气管刚度影响小,竖向隔膜对薄膜充气管刚度影响比横向隔膜大,能够显著减小薄膜充气管的挠度; 多层竖向隔膜构成的多气室薄膜充气管刚度随隔膜层数增加而增大。 薄膜充气管管径的大小直接影响薄膜充气管刚度,且对其变形影响较大,仍以中间设置竖向隔膜的薄膜充气管为例,分别取薄膜充气管直径为300 mm,400 mm,600 mm,管内气压均为80 Pa,距固定端1 800 mm 处作用垂直向下的荷载F=160 N,数值计算可得薄膜充气管管壁侧边线挠度如图9 所示。 图9 管径对悬臂薄膜充气管挠度影响 计算结果表明,管径越大,薄膜充气梁的抗弯性能越好,挠度越小,管径的变化改变了薄膜充气管截面几何性质,对薄膜充气管整体刚度的影响非常显著。 计算模型还是以中间设置竖向隔膜薄膜充气管为例,距固定端1 800 mm 处作用垂直向下的荷载F=160 N,管内气压分别取为50 Pa,80 Pa,100 Pa,400 Pa,数值计算可得薄膜充气管管壁侧边线挠度如图10 所示。 图10 气压对悬臂薄膜充气管挠度影响 计算结果表明,气压越小,薄膜充气管管壁侧边线挠度的非线性特征越明显,气压越大,薄膜充气管的刚度越大,抗弯性能越好,挠度越小,算例所取不同气压比值为8∶2∶1.6∶1,在此气压作用下充气管管壁侧边线最大挠度比值约为6.3∶3.8∶3.1∶1,具有较强的非线性。 本文对多气室薄膜充气梁受力性能进行了分析研究,采用非线性有限元法计算了多气室薄膜充气梁在不同结构参数下应力、挠度等力学性能指标,考察了梁端荷载、管径、隔膜构型等因素对多气室薄膜充气梁力学性能的影响。研究发现: 1) 采用四边形平面应力壳单元Shell63 能较好的模拟薄膜充气管受力性能,数值计算结果与工程弹性理论计算结果误差较小。 2) 外部荷载、管径、隔膜构型等因素对多气室薄膜充气管的受力性能影响较大,特别是管径、隔膜构型等结构参数在进行薄膜充气结构设计时应重点考虑。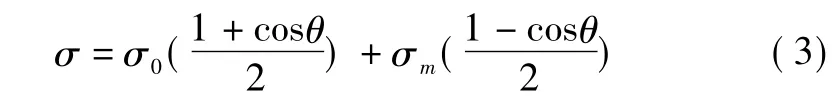

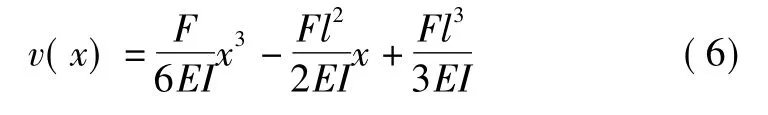
1.2 数值计算分析



2 多气室薄膜充气管数值分析

2.1 梁端荷载对应力及挠度影响

2.2 隔膜构型对挠度影响

2.3 管径对挠度影响
2.4 气压对挠度影响

3 结语