基于汉宁窗的配电网同步相量测量装置算法及应用

余高旺，方陈，樊占峰，蔺立，龚赟，朱云峰

(1. 许继电气股份有限公司，河南 许昌 461000；2. 国网上海市电力公司电力科学研究院，上海 200437)

0 引言

配电网规模增大和复杂度增高以及分布式能源并网给配电网运行带来了巨大挑战，为了适应这些新的挑战，需要新的技术手段，提升系统可观测性和可控制性，保障配电网的供电可靠性和安全性。以标准时间信号作为采样过程基准的同步相量测量技术已在输电网的动态监测，参数辨识，状态估计及协调控制等方面得到广泛应用[1-5]，值得配电网借鉴。国内外正积极探索同步相量测量技术在配电网状态估计、故障测距和定位、高阻接地故障检测、孤岛及系统振荡检测、电能质量分析、配电系统动态模型评估辨识和模型校正等方面的应用[6-10]。

国外最早开始低压配电网同步测量装置研发工作的是美国Yilu Liu教授团队，研发出了基于同步相量测量技术的频率测量网络(frequency monitoring network，FNET)，并将其应用于 110 V 的低压配电网，实现了供电系统的电压稳定分析、频率稳定分析、低频振荡分析、故障辨识、系统解列以及优化闭环控制[11]。FNET装置主要功能是基于110 V电压监控，尚未实现电流量测功能。

山东大学张恒旭研究团队在国内较早开展配网PMU研究，提出了WAMS/PMU light的概念，采用频域改进算法，以有线和无线通信方式灵活进行数据传输，目前该装置用于220 V/380 V电压等级下单相电压和频率的测量[12]。

输电网同步相量（PMU）装置的相量测量方法主要有采样值调整算法、数字滤波法、离散傅立叶变换法（DFT）、各类基于DFT的改进算法和基于泰勒级数的动态同步相量测量算法等[13-18]。由于DFT法在精度上具有显著优势，广泛应用于不同电压等级的PMU装置中，大部分DFT法是通过频率跟踪或相量修正等途径提高DFT在频偏时的测量精度，这些措施一般没有很强的抑制噪声、谐波/间谐波的影响能力。

配电网线路短，两端电压相位差在0.1°量级，有研究要求配网PMU相位测量误差小于0.1°，甚至达0.05°，高于输电网0.2°的要求。配电网更接近负荷侧,三相不平衡严重，噪声和谐波影响大，相量量测环境更加复杂和恶劣，相量计算也更加困难，用于输电网的DFT改进相量算法测量精度下降。

近年来，适用于配电网PMU的测量算法研究越来越多。文献[19]提出了一种基于频率在线分析和自适应滤波器的高精度、快响应的多通道综合同步相量算法，但计算量偏大，对硬件计算能力要求较高。文献[20]提出了一种利用三角函数多项式对误差曲线进行最小二乘法拟合的算法,但精度受修正系数的影响，无法完全补偿误差。

相比于输电网,配电网需要监测的节点众多，在配电网应用同步相量测量技术的前提条件之一是设备要简单可靠，成本低。若算法复杂,依赖高性能硬件资源,会阻碍同步相量测量技术在配电网领域的应用推广。

简单可靠、精度高、谐波及间谐波抑制能力强的测量原理算法是配网PMU装置研发的基础。

本文提出了简单实用的基于汉宁窗同步相量、谐波和间谐波算法。

1 不同窗函数的傅立叶算法幅频特性

全周傅立叶算法是电力系统中经常采用的算法。工程应用中，由于要对信号加窗进行截短，窗函数不同时，处理效果存在差异。采用矩形窗截短信号最常见，习惯上的不加窗就是使用了矩形窗。矩形窗的全周傅氏算法传递函数为

根据传递函数，矩形窗、海明窗和汉宁窗全周傅氏算法的幅频响应如图1所示。

从图1的幅频特性可以看出，海明窗和汉宁窗均有优秀的谐波、间谐波抑制能力。具体应用时，可根据需要择优选择。

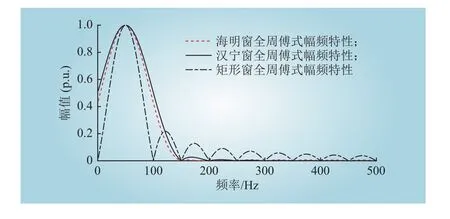
图1 不同窗函数下的全周傅立叶幅频响应Fig. 1 Full-cycle Fourier amplitude frequency response under different window functions

2 基于汉宁窗的无偏差相量算法

工程上一般采用定间隔采样获取信号。当信号频率偏离额定频率时，由于采样频率与信号频率不同步，DFT算法计算相量时出现频率泄漏现象，造成计算误差。输电网的相量算法采用误差校正抑制频率泄露时往往无法完全消除误差，特别是相位误差偏大，且一般不考虑间谐波的影响。本文提供一种消除频率泄露影响的无偏差相量算法，相位计算精度高，并具有较强的谐波，间谐波抑制能力。

由于汉宁窗全周傅氏算法抑制高次谐波、间谐波的能力强，同时为兼顾2次谐波的抑制能力，本文选用基于汉宁窗的2周傅氏相量校正算法。

上述推导过程表明，当系统频率偏移额定频率时，此算法可完全消除频率泄露的影响，计算相量无误差。同时，此算法采用了2周汉宁窗，也具有很好的谐波和间谐波抑制能力。考虑带外频率的影响，相量计算还需增加低通滤波器[21]，本文不再赘述。实际应用表明，相量的幅值和相位均具有很高的精度，相对于传统DFT相量测量算法，谐波/间谐波抑制能力强，运算量也不大，便于工程实现。

3 基于汉宁窗的谐波/间谐波算法

为了支撑配电网的电能质量分析等其他应用，配电网PMU集成了谐波/间谐波计算功能。GB/T 17626.7—2017给出了谐波/间谐波详细定义和常用的FFT计算方法。理论上，简单的FFT解决不了频率泄漏问题，测量精度很差，需要采用加窗插值的方法减少测量误差[22-25]。

加窗插值方法具有很高的精度,无论是海明窗还是汉宁窗都可以精确的计算谐波、间谐波的幅值和相位。

加窗插值是在两个相邻峰值的基础上计算得到真实的幅值和相位。当有多个信号同时存在时，实际测量到的频谱是多个信号的叠加，插值的结果不可避免的受到影响，特别是当两个信号的频率值较接近时影响较大。因此，如果考虑多个信号同时存在时，需要分析窗函数的特性，优选合适的窗函数。

从图2可以看出，汉宁窗在其他频谱上的泄露要小一些，见图2中40 Hz或60 Hz处。由于插值算法是用相邻的峰值来计算真实的信号，强信号会对弱信号的频谱计算产生较大影响。汉宁窗抑制信号间的干扰能力要强一些。

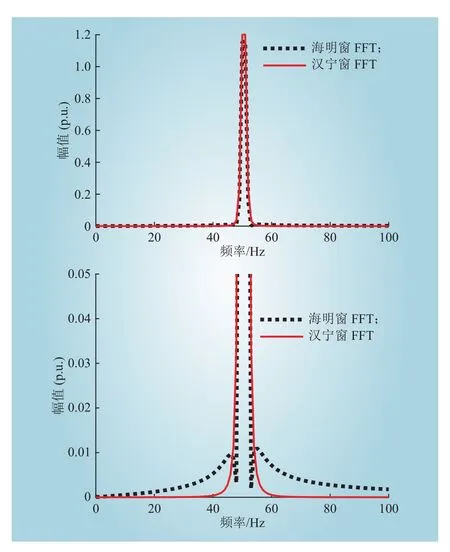
图2 不同窗函数下的FFT频谱图Fig. 2 FFT spectrum under different window functions

假设某电压信号幅值为100 V，基波频率为49.5 ～50.5 Hz，2 ～7次谐波含量均为5%。仿真分析海明窗和汉宁窗插值FFT算法在不同情况下的计算结果见表1。计算的采样率为6400 Hz，数据长度为 6400个采样点。

从表1中可以看出，当有多个信号时，海明窗插值FFT算法的相对误差最大达0.6%，超出了0.2%的测量误差要求。因此，本方案选择采用加汉宁窗插值的FFT算法计算谐波/间谐波。

表1 不同窗函数的FFT算法结果比较Table 1 Comparison of FFT results for different window functions

4 测试及验证

为了验证高精度的幅值相位测量结果，本文用Omicron试验仪搭建测试系统。设备包括：Omicron CMC-356高精度测试仪、GPS时钟装置，μm-PMU微型同步相量测量装置，模拟主站（含误差分析工具）。CMC-356试验仪输出电压/电流模拟量给μm-PMU装置，GPS时钟装置通过B码给这两台装置授时，模拟主站通过网线连接μm-PMU。

配网中应用同步相量测量技术尚无相关标准，本文借用输电网PMU装置相关的测试条件。频偏测试的范围为45 Hz ～55 Hz,谐波测试时，谐波含量为10%，谐波次数为2 ～25次。输电网PMU装置没有间谐波的测试要求，本文参考谐波的测试条件，间谐波含量为10%，间谐波频率取k次和k+1次谐波的中间值。通过模拟主站获取PMU装置的100帧/s的动态数据，解析计算出额定电压/电流附近的幅值、相位、频率、谐波值的误差范围如表2所示。

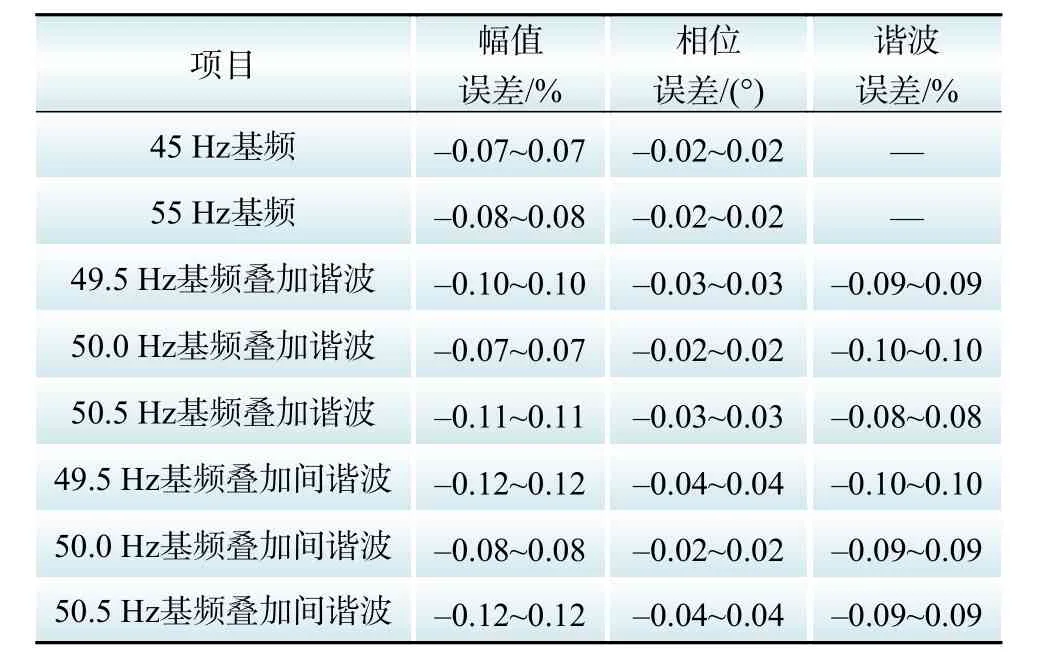
表2 误差测试结果Table 2 Error of test results

可以看出，在频率偏移下叠加谐波、间谐波时，本文提供的算法具有非常高的精度，特别是相位精度远高于输电网PMU装置。在频率偏移时，本文提供的相量算法无理论的幅值和相位误差，测试结果的误差来源于硬件采集环节。

2019年1月，采用本文算法的配电网同步相量测量装置通过了国家继电保护及自动化设备质量监督检验中心的正式实验。

5 结语

配电网相量量测环境复杂和恶劣，噪声和谐波影响大，用于输电网的DFT改进相量算法测量精度难以满足要求。本文推导出了基于2周汉宁窗的同步相量算法，不但在理论上消除因系统偏移额定值时的频率泄露影响，而且有很好的谐波/间谐波抑制效果，为配电网同步相量测量装置研制奠定基础。在谐波、间谐波测量方面，推导了加余弦窗插值FFT算法的计算公式，相对于加海明窗插值FFT算法，加汉宁窗插值FFT算法计算谐波/间谐波在抑制多信号间的互相影响上有优势。最后，搭建测试环境验证了方案的可行性。由于配电网络节点众多，从发展趋势看，需要研究配电网同步相量测量装置和配电终端的功能融合方案，提升经济效益。