基于集成学习的风电功率概率预测方法研究

杨 玉,牛洪海,李 兵,陈 霈,管晓晨

(南京南瑞继保电气有限公司,江苏 南京 211102)

0 引言

风电功率具有明显的不确定性以及随机性。传统对风电功率预测的研究主要集中在确定性的点预测。但是点预测的误差不可避免，且其结果不能对发电功率不确定性作出定量描述[1]。从目前电网的应用层面来看，含风电的电网规划、运行和安全稳定分析需要对风电功率的波动范围有比较精确的估计，因此需要能定量反映发电功率不确定性的新预测形式来克服传统点预测的缺陷。概率预测正是解决该问题的有效方式。

近年来，对风电功率概率预测的研究吸引了较多学者的关注。概率预测的建模对象通常分为两种：风电功率和风电功率点预测误差。第一种直接对风电功率实测数据进行建模，得到风电功率的分布。第二种先进行点预测，将点预测误差作为建模对象，得到误差的分布情况后嵌套至点预测结果上，形成最终的概率预测结果。常规对概率预测的研究主要基于点预测误差，并假设预测误差属于正态分布[2]、指数分布[3]，通过参数化的方法求出误差分布函数，进而得到预测区间。文献[4]使用非参数核密度估计求取预测误差的分布。上述方法计算复杂度低，但预测结果依赖于点预测的精度，容易出现泛化能力差的问题。

直接对风电功率进行概率预测的方法有多种。文献[5]使用bootstrap的方法对风电功率进行重采样，并假定输出满足正态分布，得到最终预测区间。文献[6]～文献[8]分别使用联合分位数回归，直接分位数回归，基于深度学习的分位数回归建立风电功率的分位数回归模型，并得到概率预测结果。文献[9]采用朴素贝叶斯分类获得风电功率的分类，并通过粒子群算法寻优得到预测区间的加权系数。文献[10]～文献[11]分别将预测区间的上、下限作为极限学习机、核极限学习机的输出，并通过粒子群寻优得到极限学习机的输出权重。使用风电功率自身作为建模对象，无需先进行点预测，消除了对点预测结果的依赖。本文直接对风电功率作概率预测，并在此基础上寻求结构简单的建模方法，以提高实用性。

对于概率预测评价指标，通常采用预测区间覆盖率(prediction interval coverage probability，PICP)评价预测区间的可靠性、预测区间平均宽度(prediction interval normalized average width,PINAW)以及预测区间的清晰度；采用区间平均偏差指标(interval normalized average deviation,INAD)，评价实际功率在未被预测区间覆盖下偏离区间的整体程度。对于综合评价指标，文献[12]中提出覆盖宽度准则(coverage width criterion,CWC),将PICP与PINAW进行分段式结合，但实际应用显示该指标不能科学地评估概率预测的全局性能。因此，需要寻找更为合理、有效的综合性能评价指标。

基于上述分析，本文提出一种新型的、基于集成学习的风电功率概率预测方法。基于Bagging的思想，本文将极限学习机(extreme learning machine，ELM)与分位数回归相结合，得到多个分位点的分位数回归模型，并将其作为个体学习器。同时，为了更好地评价概率预测的结果，本文使用一种新型的综合性能评价指标(new comprehensive index，NCI)[13]：通过灰狼优化算法对NCI进行极大化寻优，得到各个体学习器的最优加权系数；融合个体学习器的输出以及加权系数，得到最终的预测区间。本文所提出的方法充分结合了多种算法优势，仿真对比测试验证了其优越性。

1 极限学习机的分位数回归算法

1.1 极限学习机

与传统的神经网络不同，极限学习机会随机生成输入权重和偏置，再通过简单的矩阵运算即可获得输出权重。该方法显著提高了学习速度、降低了计算量。

(1)

式中：g(·)为激活函数；wi为输入变量与第i个隐藏节点间的权重,wi=[wi1,wi2,…,win]；βi为第i个隐藏节点与输出变量间的输出权重,βi=[βi1,βi2,…,βim]T；bi为第i个隐藏节点的偏置。

对于N个训练数据，若ELM的输出可以近似零偏差的接近实际输出。此时，有：

(2)

式(2)可进一步整理为：

Hβ=T

(3)

式中：H为隐藏层的输出矩阵，可以由式(4)表示；β=[β1,β2,…,βK]T为输出权重矩阵；T=[t1,t2,…,tN]T为输出变量矩阵。

(4)

ELM会在开始学习时随机生成输入权重和偏置，并在整个学习过程保持不变。根据式(4)可知，H的值会在开始学习时确定并保持不变。ELM通过求式(3)的最小二乘解来得到最优输出权重β*。根据广义逆理论，其解为：

β*=H+T

(5)

式中：H+为H矩阵的摩尔-彭洛斯(Moore-Penrose,M-P)广义逆，通常使用奇异值分解法(singular value decomposit,SVD)获得。

由于ELM不需要使用梯度下降法进行反复迭代，可以克服传统基于梯度的神经网络中存在的过拟合、局部最优解等问题。同时，由于其只需要通过简单的矩阵运算即可求解式(5)，明显减少了求解过程的计算负担。

1.2 基于极限学习机的分位数回归

(6)

输入变量与输出变量之间的映射关系φ(·)可由式(7)表示。

ti=φ(xi,θ)

(7)

式中：θ为模型参数。

τ分位点的回归参数的估计问题可以转化为式(8)所示的优化问题。

(8)

式中：ρτ(·)为检验函数。

(9)

根据上文ELM的推导过程可知，ELM可随机生成输入权重和偏置。若输入变量值已知，式(3)中的H为确定值，待求解的输出权重β与输出变量间可看作是线性关系。将多入单出的ELM网络模型代入式(8)中，即可得到极限学习机分位数回归的目标函数：

(10)

式中：Hi为H矩阵的第i行。

目前，求解线性分位数回归的方法主要有单纯形法、内点法以及平滑算法。内点法以其运算效率高、数值稳定等特点，得到了广泛应用。本文使用内点法求解极限学习机分位数回归模型。

(11)

将式(11)整理为标准的线性规划形式：

min(cTd)s.t.Ad≤b

(12)

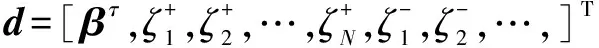
使用内点法对上述线性规划进行求解，即可得到τ分位点回归参数βτ。

2 风电功率概率预测模型的建立

2.1 新型综合性能评价指标

(13)

传统的预测区间评价指标主要包括可靠性和清晰度，本文在此基础上使用一种新型综合性能评价指标。

①可靠性。

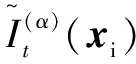
(14)

式中：Ψ为测试样本的PICP;Ntest为测试样本的个数。

(15)

为了保证预测区间有高可靠性，PICP应当尽可能接近PINC。另外一个相关的指标为平均覆盖误差(average coverage error，ACE)。其定义如式(16)所示。

Λ=Ψ-Ω

(16)

式中：Λ为测试样本的ALE，应当尽可能地接近0，以保证预测区间的可靠性；Ω为设定的PINC。

②清晰度。

当预测区间的宽度越宽，区间的可靠性就越高。但是过宽的区间在实际应用中意义不大。这是因为它并不能真正地反映输出变量的不确定信息。因此，需引入预测区间宽度的评价指标。

(17)

(18)

每个预测输出均可通过式(18)得到区间分数。对于全部测试数据而言，全局区间分数可通过式(19)获得。

(19)

区间分数既考虑了预测区间的宽度，又兼顾了预测区间外的累积偏差，从而能更加合理地表述预测区间的性能。

③新型综合性能评价指标。

在实际应用中，期望的预测区间应当是可靠性高(ACE尽可能接近0)并且区间分数较高。这对后续优化才会更有意义。对于综合评价指标而言，应该能够兼顾可靠性与清晰度，并自适应地分配不同情形下考核的重点。基于上述目的，本文中使用一种新型综合性能评价指标[13]。其表达式如式(20)所示。

(20)

(21)

在选择合适的η、σ后，当ACE与0偏差较小时，RIS趋近于0。此时，RIS对综合性能指标影响较小，主要考核的为区间分数。当ACE与0偏差较大时，RIS突增。此时，RIS对综合性能指标影响较大，主要考核的为可靠性。因此，本文使用的新型综合性能评价指标能够根据情况自适应地调整考核重点。

2.2 基于集成学习的概率预测模型建立

2.2.1 概率预测模型结构

集成学习可获得优越性能的重要条件是个体学习器的多样性以及差异性。个体学习器多样性的产生方式主要有3种：数据多样性、参数多样性与结构多样性。

本文提出的新型概率预测模型结构如图1所示。

图1 新型概率预测模型结构Fig.1 Novel probabilistic prediction model structure

本文将极限学习机分位数回归作为个体学习器，通过设定不同的分位点获得多个个体学习器。由于极限学习机会随机生成输入权重和偏置，并且不同分位点回归的目标函数不同，本文所构造的个体学习器可以满足参数与结构多样性，同时个体学习器间不存在强依赖关系。

根据文献[5]的描述，假设预测输出属于正态分布，则满足置信度为100(1-α)%下的预测区间可通过式(22)获得。

(22)

(23)

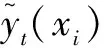
(24)

(25)

2.2.2 概率预测模型求解

通过上述推导可知，加权系数的选取将会直接影响预测区间的范围。因此，加权系数的整定将是概率预测过程中的重要一环。

概率预测模型计算流程如图2所示。

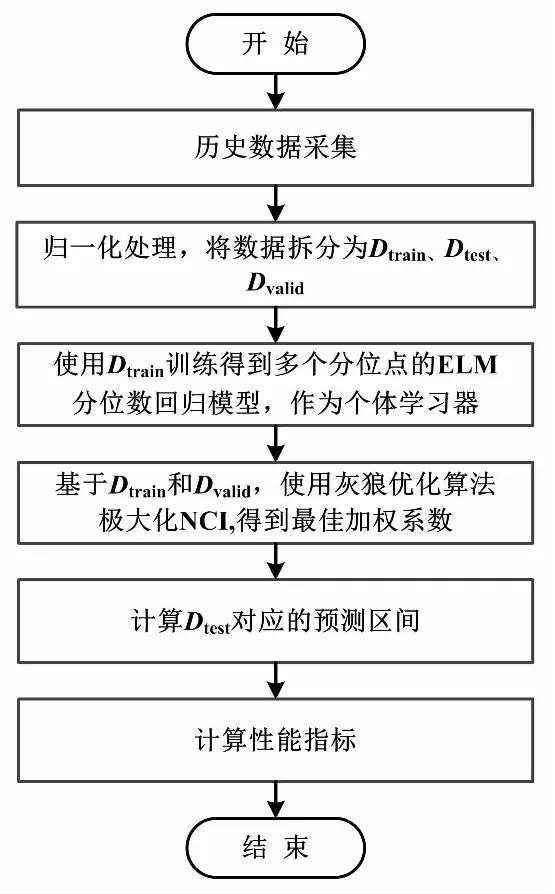
图2 概率预测模型计算流程图Fig.2 Flowchart of probabilistic prediction model calculation

灰狼优化算法由于具有收敛性强、参数少、易实现等特点，被广泛应用于各种寻优场景。本文采用灰狼优化算法，通过极大化NCI得到最优的加权系数。为了避免过拟合，本文把数据集分为Dtrain、Dvalid和Dtest这3类。

3 算例测试

3.1 仿真数据及参数设定

本文使用江苏省某风电场2018年以及2019年的历史数据进行仿真测试，参数如下。数据采样周期为15 min。风速使用70 m测风塔采集的平均风速。风电功率使用数据采集与监视控制(supervisory control and data acquisition,SCADA)系统采集的实际数据。该风场的总装机容量为202 MW，包含37台4 MW以及18台3 MW的风机。

个体学习器的个数设定为19个，分位点为0.05～0.95，间隔为0.05。Dtrain包含4 000组数据，使用的是2018年7～8月份的数据。Dvalid包含480组数据。为了增加泛化能力，使用的是2019年7～8月份的数据。Dtest使用960组2019年的数据。

3.2 预测结果

本文通过使用灰狼优化算法极大化NCI，得到最优的加权系数。在90%与80%置信度下，NCI随迭代次数的变化曲线如图3所示。由图3可知，随着迭代次数的增加，NCI逐步趋于最大值。

图3 NCI随迭代次数的变化曲线Fig.3 NCI veriation curves with different iteration numbers

测试数据Dtest在90%和80%置信度下的预测结果如图4所示。

图4 预测结果示意图Fig.4 Schematrc diagram of prediction results

由图4可知，预测区间较窄且区间外的点距离区间边界也较近。

性能指标计算结果如表1所示。

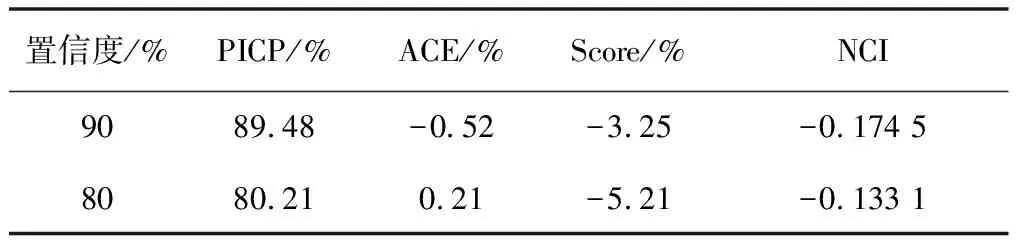
表1 性能指标计算结果

计算结果显示，ACE基本趋近于0，根据式(19)计算得到的区间分数(Score)以及式(20)计算得到的综合性能评价指标也较高，充分说明基于本文所提出的算法可以获得有效的预测区间。

3.3 预测结果

本文中的个体学习器使用的是不同分位点的分位数回归模型。基于个体学习器，将本文所提出的寻优加权融合策略与2种典型的方法进行对比。性能指标对比结果如表2所示。平均加权法是对每个个体学习器赋予相同的权重，并通过式(22)～式(25)的计算得到预测区间。直接分位法是将0.95以及0.05分位点作为90%置信度下的预测区间的上下限，0.9以及0.1分位点作为80%置信度下的预测区间的上下限。

表2 性能指标对比结果

从表2可知，平均加权法在80%置信度下，可靠性以及区间分数都比较高；但是在90%置信度下，区间分数较高但是可靠性比较差。直接分位法在90%置信度下的结果优于平均加权法，但在80%置信度下的结果则较差。上述结果说明平均加权法以及直接分位法对不同置信度的适应性较弱，且与本文所提出的算法相比，在可靠性、区间分数以及NCI上均不占优。该结果也充分说明多个体集成学习的优势以及寻优加权的有效性。

不同算法的详细性能指标计算结果如表3所示。

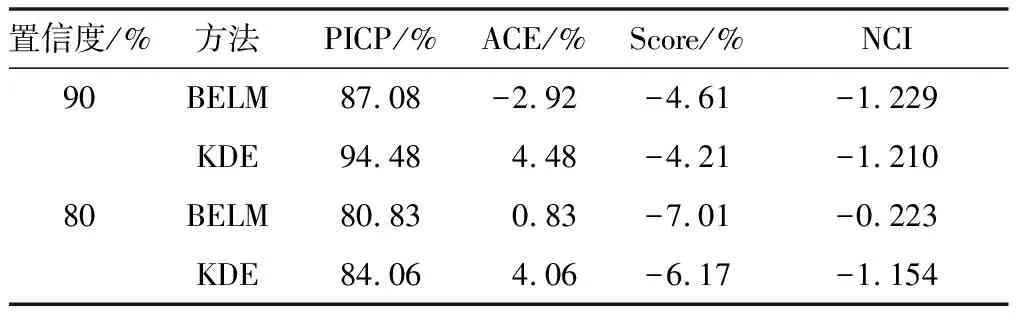
表3 不同算法的详细性能指标计算结果

基于Bootstrap的极限学习机(Bootstrap extreme learning machine，BELM)算法首先使用Bootstrap对训练数据进行重采样，然后通过ELM建立每一组采样数据的模型，最后假定输出满足正态分布，以得到预测区间。基于非参数核密度估计(kernel density estimation，KDE)算法首先对风电功率进行点预测，然后对点预测误差进行非参数核密度估计，最后与点预测结果相结合得到预测区间。KDE算法依赖于点预测的精度，而通过训练数据得到的预测误差分布通常并不适用于测试数据。由表3可知，KDE算法的可靠性虽然较高但是预测区间较宽，所以对应的NCI较小、得到的预测区间有效性较弱。对于BELM算法，90%置信度下与KDE算法的区间分数相似但可靠性较差，80%置信度下的结果整体优于KDE算法。由于Bootstrap采用随机抽样，所以最终得到的结果容易出现不稳定的情况。结合表1的计算结果，本文提出的算法在各项指标上均优于上述2种算法，能够在确保高可靠性的同时，获得较窄的预测区间。这也进一步说明了基于新型综合评价指标优化后的预测区间更加有效。

4 结论

为了获取有效的风电功率概率预测结果，本文提出一种新型的基于集成学习的概率预测方法，其主要特点如下。

①充分利用极限学习机的快速学习以及较强的泛化能力，有效地获得分位数回归模型。

②使用了新型的综合性能评价指标，能够根据不同情况自适应地调整考核重点，从而更加合理地兼顾可靠性和清晰度。

③提出了新型基于集成学习的概率预测模型结构。基于新型综合性能评价指标，通过灰狼优化算法得到加权系数，充分融合了多种算法优势。

本文利用风电场实际运行数据进行了仿真研究和对比分析。结果表明，本文方法可提供更为有效的预测区间，综合性能具有明显优势，能够为电网的安全、稳定运行提供有效的数据支撑。