ECQ网络中嵌入哈密顿圈的高效算法研究

周东仿

(1.上海出版印刷高等专科学校出版传媒研究院，上海 200093；2.苏州大学计算机科学与技术学院，江苏 苏州 215006)

0 引言

互连网络的拓扑结构一直是并行计算领域研究的热点，受到了国内外学者的广泛关注。迄今为止，人们陆续提出了多种互连网络拓扑结构，如超立方体网络(Hypercube)[1]、交叉立方体(crossed cube，CQ)网络[2]、莫比乌斯立方体(Mobius cube，MQ)网络[3]、扭立方体(twisted cube，TQ)网络[4]。这几种n-维的互连网络的链路数均为n2n-1。为了既降低网络成本开销又保持网络性能不受影响，同时减少网络连接的复杂度，Loh等进一步在超立方体网络基础上有条理地删除一些边，构建了一种新的网络——交换超立方体(exchanged hypercube，EH)网络[5]。在维度相同的情况下，与超立方体网络相比，EH网络的链路数约为超立方体网络链路数的一半，而直径与超立方体网络的直径近似相等。

为了既降低网络直径又减少网络构造成本，以保持良好的网络性能，Li等[6]在CQ网络基础上构建了一种新的网络，即交换交叉立方体(exchanged crossed cube，ECQ)网络。该网络既保持了CQ网络的许多优越性质，又融合了EH网络的良好性质。首先，ECQ网络的直径为同维EH网络直径的一半，与同维CQ网络的直径几乎相等。其次，ECQ网络的链路数约为同维CQ网络的链路数的一半，与同维EH网络的链路数相等。另外，ECQ网络还具有良好的可扩展性、可分割性、同构性[6]、可嵌入性[7-8]和可诊断性[9]等。

一个互连网络可以用一个简单无向图G来表示。图G的顶点V(G)表示网络中的处理器(或处理机)，边E(G)表示处理器(或处理机)之间的通信链路。若圈C包含图G中所有顶点一次且仅一次，则称G具有哈密顿性质、圈C为哈密顿圈。

如果在网络的路由算法中使用哈密顿圈，则能够减少或避免死锁和拥塞，提高通信效率[10]。其次，哈密顿性问题可视为不交路径覆盖问题的一个特例。例如一对二不交路径覆盖性问题本质上就是哈密顿性问题。再者，如果在互连网络或数据中心网络的故障诊断中使用哈密顿性质，则能降低该网络故障诊断的次数，实现该网络的故障检测与快速定位，从而进一步提高该网络故障诊断的效率。除此之外，哈密顿性质也可应用在计算机科学编码中[10]。因此，研究网络的哈密顿性质具有重要价值。但是，并不是所有的网络都具有哈密顿性质，且如何判定一个网络是否具有哈密顿性质的充分必要条件也是不存在的。哈密顿圈或哈密顿路径的求解也是一个多项式复杂程度的非确定性多项式(non-deterministic polynomial，NP)问题[11-14]。

尽管对一般互连网络哈密顿性质的求解问题是NP完全问题，但是对一些特定网络中的哈密顿问题求解已经得到解决。本文研究了ECQ网络的哈密顿性质，给出了在ECQ网络中构造哈密顿圈的算法。具体是：给出了当s≥3并且t≥3时，从ECQ网络中任意一个结点出发即可高效地构造出哈密顿圈;分析了当1≤s≤2并且s≤t时，从ECQ网络中任意一个结点出发哈密顿圈的构造算法，也考虑了所有情形，确保了研究问题的完备性；通过模拟试验，对该算法进行了验证。

1 准备工作

定义1.1 设u=u1u0、v=v1v0，u、v均为二进制字符串。若满足(u,v)∈{(00,00),(10,10),(01,11),(11,01)}，那么称u与v是相关的,记为u～v[2]。

①当n为偶数时，un-2=vn-2。

X3和X4如图1所示。

图1 X3和X4

根据文献[6]和ECQ网络的基本性质，对ECQ网络进行如下定义。

定义1.3 (s+t+1)维的ECQ网络可表示为:ECQ(s,t)=(V,E)。其中：s≥1且t≥1；V为顶点集，V={as-1...a0bt-1...b0c|ai,bj,c∈{0,1},i∈[0,s- 1],j∈[0,t- 1]}；E为边集，由三种边集(E1、E2和E3)组成，且E1、E2和E3互不相交，E=E1∪E2∪E3。ECQ网络中任意两个顶点u与v，有u、v∈V。

边集E1、E2和E3定义如下。

①(u,v)∈E1,有且只有u[0]≠v[0]，u⊕v=1。其中，⨁表示异或操作。

②(u,v)∈E2,有且只有u[t:1]=v[t:1],u[0]=v[0]=0,并且(u[s+t:t+1],v[s+t:t+1])∈E(Xs)。

③(u,v)∈E3,有且只有u[s+t:t+1]=v[s+t:t+1],u[0]=v[0]=1，并且(u[t:1],v[t:1])∈E(Xt)。

由以上的定义可知，ECQ(s,t)具有2s+t+1个顶点、(s+t+2)2s+t-1条边，并且ECQ(s,t)和ECQ(t,s)是同构的，一个ECQ(s,t)可分成2s个Xt和2t个Xs[6]。ECQ(2,3)如图2所示。图2中：虚线表示E1边；细实线表示E3边；粗实线表示E2边。

为了简便，不妨假设s≤t,把“as-1...a0bt-1...b0c”简写成“abc”。

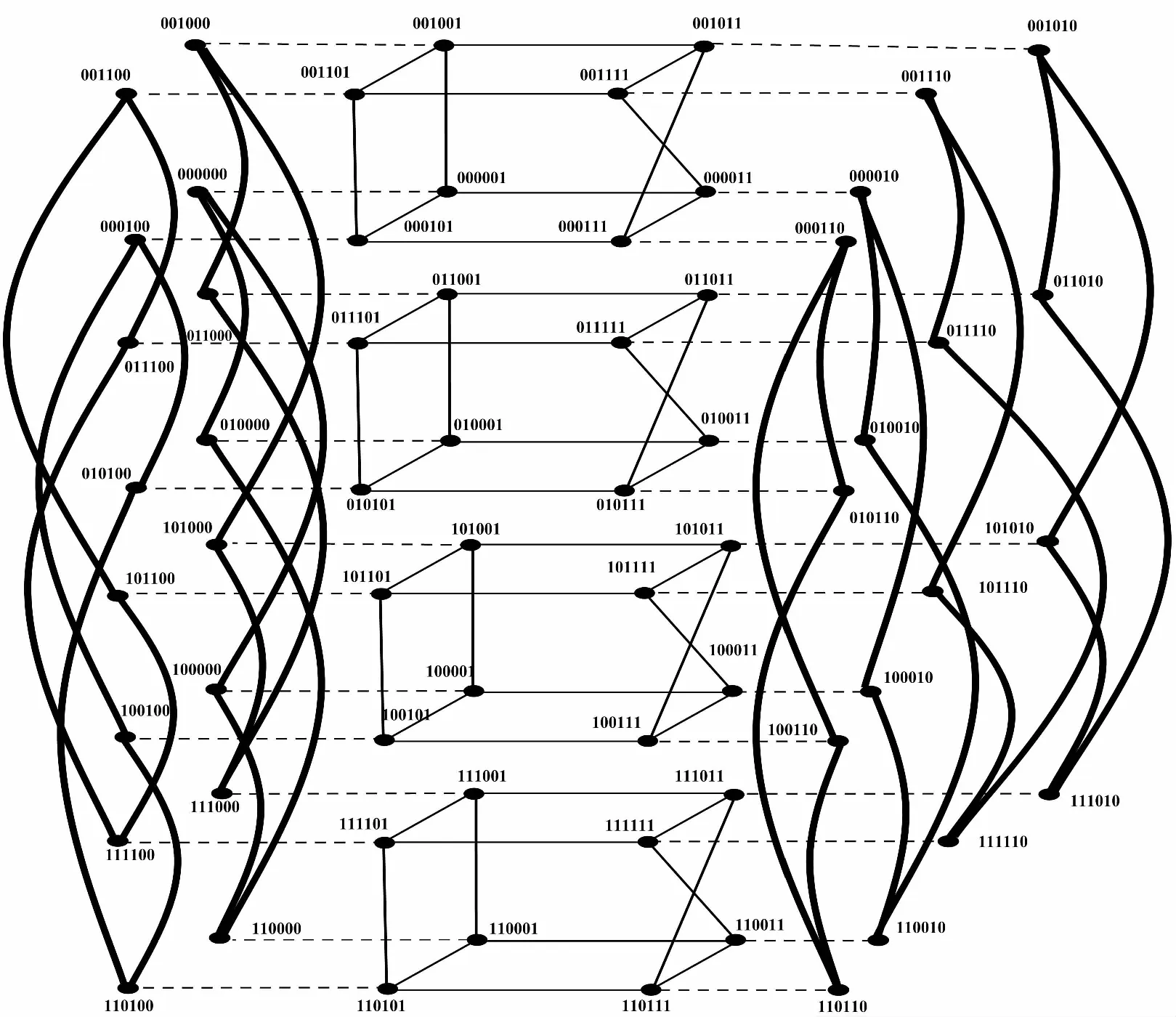
图2 ECQ(2,3)

2 哈密顿圈算法设计

Chen等给出了在Xn中时间复杂度为O(n)的求解哈密顿圈的LGC算法[13]。其基本思想如下。

(1)设πn=(d1,d2,…,dn)是1,2…n的一个随机排列，满足:①min(dn-1,dn)为奇数； ②|dn-1-dn|=1。

(2)构造以下数列。

RLπ(1)=d1，RLπ(i)=RLπ(i-1),di,RLπ(i-1)(2≤i≤n),RLπ=RLπ(n)=(p1,p2,…,p2n-1)。

(3)对任一点u,ui=neighbor(ui-1,pi)。

(u0,u1,…,u2n-1)为Xn中的哈密顿回路。

当3≤s≤t时，首先在Xn基础上，按照LGC算法构造Xn的哈密顿圈。方法如下。

假设(a0,a1,…an-1)、(b0,b1,…bm-1)分别为Xs和Xt中构造出的哈密顿回路(其中n=2s,m=2t)。则按照LGC算法以及ECQ(s,t)的定义，构造如下。

a0b00→a0b01→a0b11→a0b10→a1b10→a1b11→…→a1bm-10→a1bm-11→a1b01→a1b00→a2b00→a2b01→a2b11→a2b10→a3b10→a3b11…→a3bm-10→a3bm-11→a3b01→a3b00→…an-2b00→an-2b01→an-2b11→an-2b10→an-1b10→an-1b11→…→an-1bm-10→an-1bm-11→an-1b01→an-1b00→

以上即为ECQ(s,t)上的哈密顿回路。由于该构造方法是根据ECQ(s,t)的定义在常数时间内即可构造完成，所以该算法是高效的。进一步考虑了1≤s≤2的情形。当1≤s≤2且s≤t时，设计了FindHcycle算法，即考虑了所有情形。

算法:FindHcycle

输入:ECQ(s,t)上任意一个结点，且满足1≤s≤2，s≤t。

输出:若存在一个哈密顿圈HC，则输出并返回。

a←ECQ(s,t)中第一个结点；

v←a；

l←0；

s.push(v)；

flag←1；

while(stack s is not empty) do

v=s.peek();

ifl=2s+t +1-1

then ifv与a相邻

then return HC；

elsev←s.pop()；

flag←0；

l←l-1；

end if

elsev←next(v);

ifv!=null and flag !=true

thens.push(v)；

flag =true；

l←l+1；

elsev←s.pop()；

flag←0;

l←l-1；

end if

end if

end while

3 仿真试验

通过仿真试验，对FindHcycle算法和证构造算法进行有效性和正确性验证。试验环境是内存为8 GB、CPU为Intel(R) Core(TM) i5-3320M/4核/2.60G Hz的笔记本电脑，操作系统为64位Windows 7系统。该试验揭示了如何在ECQ(s,t)网络上使用FindHcycle算法和构造算法快速构建出哈密顿圈。按照ECQ网络的定义，首先模拟构造出ECQ(2,3)网络、ECQ(3,3)网络。当ECQ网络的规模更大时，该构造算法也能给出相应的运行结果。因篇幅有限，更大规模的ECQ网络结点数目较多，不再进行列举。

对于ECQ(3,3) 网络,运行上述构造算法相应的程序，如在其中任选取一个顶点(如0001100)为起点，得到的哈密顿圈如下。如<0001100 ,0001101,0000101,0000100>表示ECQ(3,3)中起点为0001100、终点为0000100的一条路径。以此类推，为了节省空间，省去了“，”。下同。

<0001100 0001101 0000101 0000100

1000100 1000101 1000001 1000000 0000000

0000001 0001001 0001000 1001000 1001001

1001011 1001010 0001010 0001011 0000111

0000110

1000110 1000111 1000011 1000010 0000010

0000011 0001111 0001110 1001110 1001111

1001101 1001100 1101100 1101101 1100101

1100100 0100100 0100101 0100001 0100000

1100000 1100001 1101001 1101000 0101000

0101001 0101011 0101010 1101010 1101011

1100111 1100110 0100110 0100111 0100011

0100010 1100010 1100011 1101111 1101110

0101110 0101111 0101101 0101100 0111100

0111101 0110101 0110100 1010100 1010101

1010001 1010000 0110000 0110001 0111001

0111000 1011000 1011001 1011011 1011010

0111010 0111011 0110111 0110110 1010110

1010111 1010011 1010010 0110010 0110011

0111111 0111110 1011110 1011111 1011101

1011100 1111100 1111101 1110101 1110100

0010100 0010101 0010001 0010000 1110000

1110001 1111001 1111000 0011000 0011001

0011011 0011010 1111010 1111011 1110111

1110110 0010110 0010111 0010011 0010010

1110010 1110011 1111111 1111110 0011110

0011111 0011101 0011100 0001100>。

对于ECQ(2,3) 网络,运行FindHcycle算法对应的程序，如在其中任选取一个结点(如101100)为起点，得到的哈密顿圈如下。

<101100 101101 100101 100100 110100

110101 110111 110110 100110 100111 100011

100010 110010 110011 110001 110000 100000

100001 101001 101000 111000 111001 111011

111010 101010 101011 101111 101110 001110

001111 001011 001010 011010 011011 011001

011000 001000 001001 000001 000000 010000

010001 010011 010010 000010 000011 000111

000110 010110 010111 010101 010100 000100

000101 001101 001100 011100 011101 011111

011110 111110 111111 111101 111100 101100>。

仿真试验进一步验证了本文构造算法和算法FindHcycle的有效性和正确性。

4 结论

本文给出了在ECQ网络中求解哈密顿圈的构造算法，通过仿真试验实现了该算法并给出了试验结果，进一步验证了算法的正确性和有效性，为该网络高效地通信提供理论参考依据[15]。

由于在网络中发生故障是不可避免的，基于当前研究成果，下一步研究将考虑ECQ网络的容错哈密顿性质。