电传动矿车永磁同步发电机调压系统

房康宁，李斌，张莉

（徐州徐工矿业机械有限公司，江苏 徐州 221000）

1.前言

电传动矿车是露天矿山的主要运输设备，其传动系统为：发动机-发电机-整流器-逆变器-电动机。目前在电传动矿车中广泛使用的发电机主要有两种技术路线：西屋制动公司的三次谐波励磁发电机和西门子公司为代表的无刷励磁发电机，均为电励磁发电机[1]。随着永磁电机在地铁、高铁等领域的稳定应用，将永磁发电机应用于电传动矿车也成为现实。永磁发电机较电励磁发电机，没有电励磁的复杂系统，在成本和可靠性上有很大优势[2]。

传统的PID和自适应控制受控制对象的参数影响较大，控制方式相对复杂，而滑膜控制对被控对象的参数变化不敏感，鲁棒性好等特点，因此在电机控制测量中使用较多。滑膜控制的思想是控制被控对象的运行轨迹按照预定的切面运动，直至达到平衡状态。传统的滑膜控制方法在目前应用情况下存在抖动问题，影响电机控制性能。如果想要抑制抖振问题，不仅要对滑膜运动的轨迹进行分析，还要对某一时刻的滑膜运动进行有效性分析，了解是以何种形式向切换面运动的，而趋近率控制技术的发展，为滑膜控制的研究指明了方向，所以通过对趋近率的值进行有效调整，可以抑制该问题。

由于永磁同步发电机由于磁场的不可控性，其稳压问题在电传动矿车的应用中尤为突出，直接影响后端电机功率和电驱系统功率输出，本文通过对永磁发电机和PWM整流器进行研究并建立数学模型[3]，对整流系统控制策略进行研，分析传统滑膜控制存在的问题，提出使用趋近率的控制策略以改变控制效果，考虑将系统的状态变量纳入控制系统，当系统状态变量在向平衡点有序接近时，趋近率也会随着降低为零，从而控制了系统的“抖振”问题，保证负载变化时，整流后直流电压的稳定性，并将该控制策略在车辆上进行实验验证。

2.永磁同步发电机和PWM整流器数学模型

2.1 永磁同步发电机数学模型[4]

电传动矿车使用的永磁同步发电机为三相星形连接，将永磁同步发电机等效为三相相差120°电压源，其每相的等效反电势、等效电感、等效电阻分别由发电机反电势、相电感、相绕组电阻等效产生，所以可以建立相应的三相电压型PWM整流器等效模型进行分析。

为了建立永磁发电机的d-q轴数学模型，进行如下假设：（1）发电机的磁路是线性的；（2）忽略发电机铁芯饱和与漏感；（3）忽略发电机的铁芯损耗和磁路损耗；（4）发电机的气隙磁场是正弦分布；（5）忽略发电机转子的阻尼绕组。

其电磁关系为：

隐极同步电机，A相定子绕组与a相转子轴线之间的电角度为：

磁链方程：

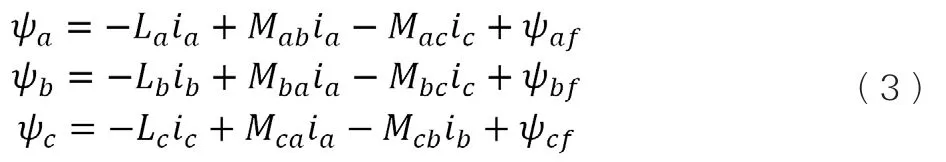
电磁转矩方程：

机械运动瞬态方程：

2.2 三相PWM整流器的数学模型[5]

首先做以下假设，用于建立数学模型：

（1）电动势值分别为ea、eb、ec，为正弦波，三相相差120°；

（2）忽略线型电感Ls饱和情况；

（3）能量双向传输时，直流侧负载由(电阻)和(直流电动势)串联组成。

图1 电压型PWM整流器拓扑结构

对于三相电压型的PWM整流器，一般使用开关函数来建立其数学模型。但是用开关函数建立的数学模型，在功率开关器件开通与关断的过程中，会产生对系统不利的低频分量和高频分量。根据实际应用的控制经验，可以忽略其中的高频分量，只考虑其中的低频分量，即可获得适用于系统控制分析的低频数学模型。

下文对三相电压型PWM整流器数学模型进行分析，由开关函数方法建立。

2.3 PWM整流器的工作原理[6]

电压型PWM整流器由三相桥臂构成，每个桥臂均有上下两个IGBT功率开关器件组成，而每相桥臂只允许有三种开关状态，上下桥臂开关器件都关断和上下桥臂分别单独开通，除去都关断情况，六个器件的开关状态可以组合出8种矢量，因此开关函数可以用下面方程来表示sk：

式中sk=1时，上侧功率开关器件导通工作，下侧功率开关器件关断；sk=0，上侧功率开关器件关断，下侧功率开关器件开通。

根据基尔霍夫电压定律和整流器特性，可以得到三相回路方程：

A相：

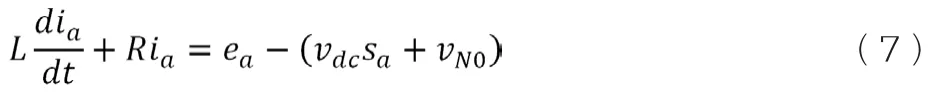
B相：

C相：

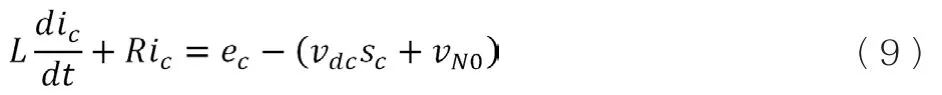
根据负载的对称性可知：

将式（7）-式（10）联合，可得：

在系统的任意时刻，都有三个开关管导通，并且有8种开关模式，通过计算，母线电压可描述为：

最后，对直流母线的正极应用基尔霍夫电流定律，可得：

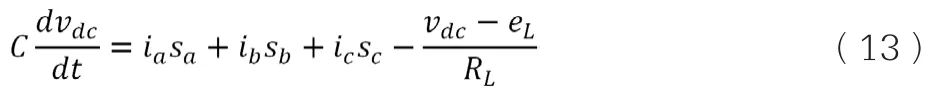
联合式（7）-式（12），可以得到在三相静止坐标系下，三相电压型PWM整流器的开关模型：

将三相(a，b，c)坐标系下三相PWM整流器的开关函数模型转换成同步旋转的(d，q)坐标系下的模型，可得：

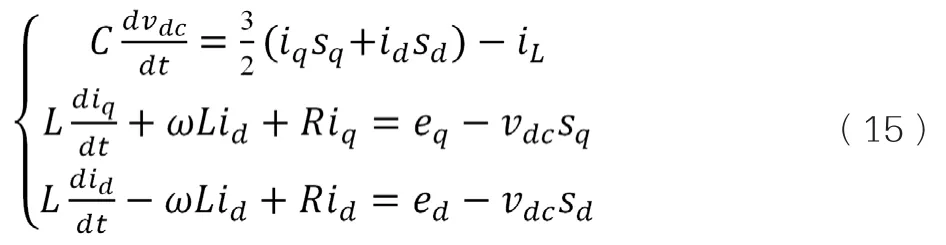
为获得线性化描述，定义新变量vd、vq，令

得三相PWM整流器在d-q轴坐标系中的更容易进行控制分析的数学模型：

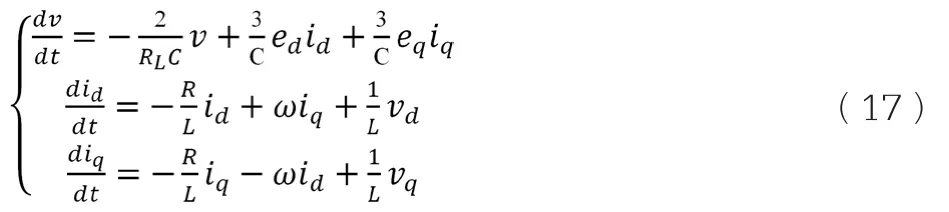
3.新型趋近率滑膜控制技术

传统滑膜控制在平衡点处存在“抖振”问题，采用新型趋近率电压滑膜控制器。普通趋近励率表达式：

要想提高系统状态的稳定性，需要把系数k1改为eq(x1,s),其为可变系数，得到新型趋近率表达式为：

3.1 趋近率抖振分析及控制

根据新的滑膜控制方法，滑膜切换面函数|s|处于正向增加时，系统的状态与所控制的切换面处于相悖状态，函数eq(x1,s)的值向常数k/ε接近，而0＜ε＜1所以k/ε＞k，可以看出来，新的控制方法系统的趋近速度得到了提高。另一种情况，函数|s|处于下降时，系统的状态与所控制的切换面接近时，函数eq(x1,s)的值与|x1|·k接近，当|x1|下降的时候，趋近率向0靠近，系统也向平衡状态稳定。文献［7］提出的趋近率在上述状态下接近于|x1|·k/（1+|x1|），因为|x1|·k≥||x1|·k/（1+|x1|），在文献[7]的基础上，本文选取了一种新的控制策略，其效果是使系统的趋近速度得到了大幅提升，同时系统的状态也平稳状态迅速接近，也就是接近于0，,在此过程中，新趋近率eq(x1,s)的值也会向0快速趋近，整个过程中，系统的抖振问题得到较好控制。所以在控制系统不断向稳定状态发展的过程中，根据滑膜控制切面的变化情况，系统的趋近率的变化范围仅在0和k/ε之间，当达到状态平衡点时，滑膜趋近率的值也变为0，从分析过程可以看出，传动控制中的抖振问题得到有效控制。

3.2 新型趋近率稳定性分析

稳定性分析依据李雅普诺夫理论，定义V=s2/2为李氏函数。滑膜控制器稳定的条件是

将改进型趋近率代入式（21）中，得到

从式（22）可以看出，其值不大于零，所以本文提出的新型趋近率控制策略是可行的，系统是稳定的。

3.3 新型趋近率电压滑膜控制器设计

定义电压误差：

定义滑膜切换面：

对切换面进行微分：

根据电压微分方程，可得：

永磁发电机，所以id=0，,得到滑膜控制表达式：

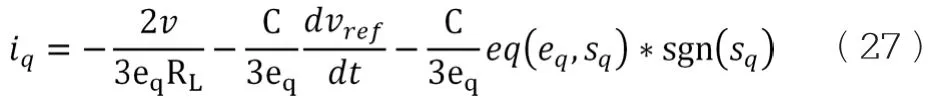
4 实验验证

发动机在怠速750rpm时，中间电压随着负载变化波动很大，红色曲线为直流母线电压。

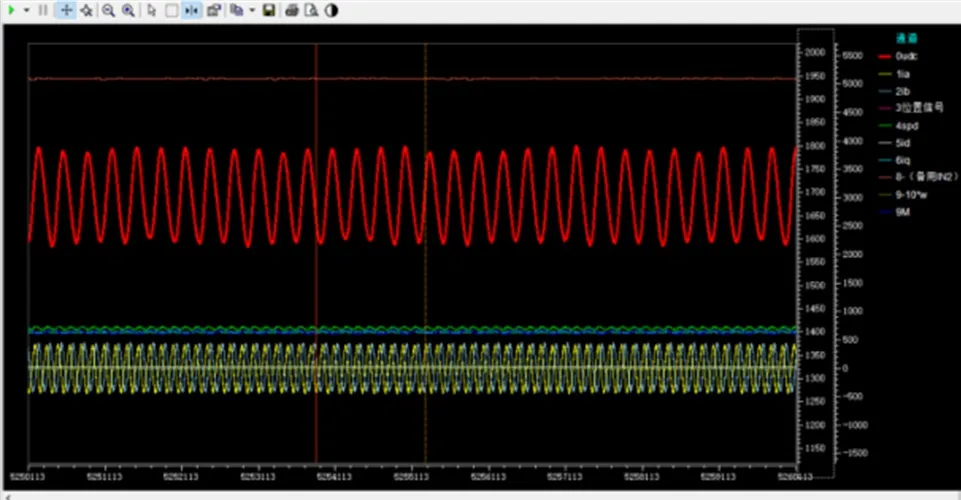
发动机在1900rpm时，中间电压随着负载变化波动很大，红色曲线为直流母线电压。

使用新型趋近率滑膜控制技术之后，发动机在1900rpm，不同负载情况下，中间电压均可以稳定在1600V，红色曲线为直流母线电压。

5 结论

由试验结论可以看出，如果不对整流系统进行有效控制，在发动机处于怠速时，中间电压波动很大；在发动机处于高转速时，负载变化同样会对中间直流母线电压造成很大影响，对后续电机的控制带来很大挑战。加入新型滑膜控制策略之后，在负载变化时，使用新型趋近率滑膜控制技术可以有效抑制直流母线电压波动，使其稳定在目标电压。