平行泊车系统轨迹规划与运动控制方法

陈文强

(福建汉特云智能科技有限公司，福建 福州 350007)

随着汽车保有量的不断攀升，城市交通中泊车难的问题日益突出。自动泊车系统(automatic parking system，APS)作为自动驾驶辅助技术，集车辆感知、路径规划和运动控制于一体，能有效解决停车对驾驶员造成的困扰[1]。

在泊车规划方面，Chen等[2]基于改进遗传算法和时间增强的A*(Hybrid A Star)算法解决高密度停车场路径规划问题，有效提高了泊车效率和安全性。Jang等[3]将轨迹规划问题视为由车辆动力学模型和可行驶区域约束组成的约束优化问题，基于内点法求解平行停车轨迹[3]。郭奕璀[4]基于模型预测控制(model predictive control，MPC)的动态窗口法进行泊车速度规划，实现对路径的局部动态调整，同时满足运动学约束[4]。在运动控制方面，Chen等[5]提出了一种新的自适应伪谱(NAP)方法，基于时间-能量最优控制模型求解停车时间和能量的最小化，仿真结果表明所提方法相比内点法和分段高斯伪谱法具有更高的计算效率和精度[5]。冯欣阳等[6]选用指数趋近率设计滑模控制器，利用连续函数代替符号函数来降低抖振影响，仿真表明车辆能够连续、无突变地完成泊车操作，抖振抑制效果较好[6]。国内外学者在泊车路径规划与运动控制方面有诸多成果，但多数仅对泊车轨迹规划或纵/横向控制进行针对性研究，缺少一套从泊车轨迹规划到控制的完整、可行的解决方案。

本研究针对平行泊车场景提出泊车轨迹规划与运动控制策略：在规划层通过几何法及三次样条插值进行泊车路径规划，并基于二次规划求解满足泊车过程约束的最优速度曲线；在控制层建立车辆运动学模型，设计PID纵向控制器和MPC横向控制器，实现对期望轨迹的精确跟踪，最后进行Prescan/Simulink联合仿真验证。

1 车辆建模

考虑泊车过程为低速行驶，无需考虑车辆稳定性等动力学因素，因此基于运动学模型构建规划与控制的车辆模型，如图1所示。

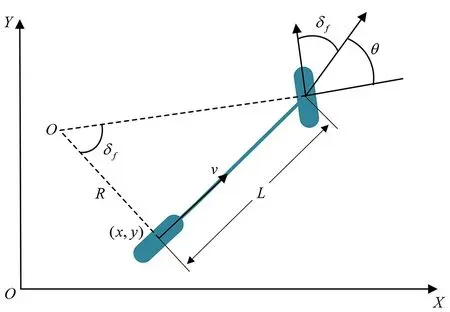
图1 运动学模型Fig.1 Kinematic model

建立XOY惯性坐标系， 则车辆运动学模型可表示为[7]：

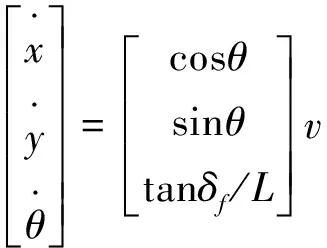
(1)

其中，(x,y)为车辆后轴中心定位点，L为车辆前后轴中心之间的轴距，v为车辆后轴中心沿纵向方向的速度，θ为车辆当前横摆角，δf为前轮转角，R为转弯半径。

2 泊车轨迹规划

2.1 泊车路径规划

采用圆弧切直线法[8]进行平行泊车路径规划，并基于三次样条插值实现曲率连续。

2.1.1 平行泊车路径规划

圆弧切直线法的数学模型如图2所示。

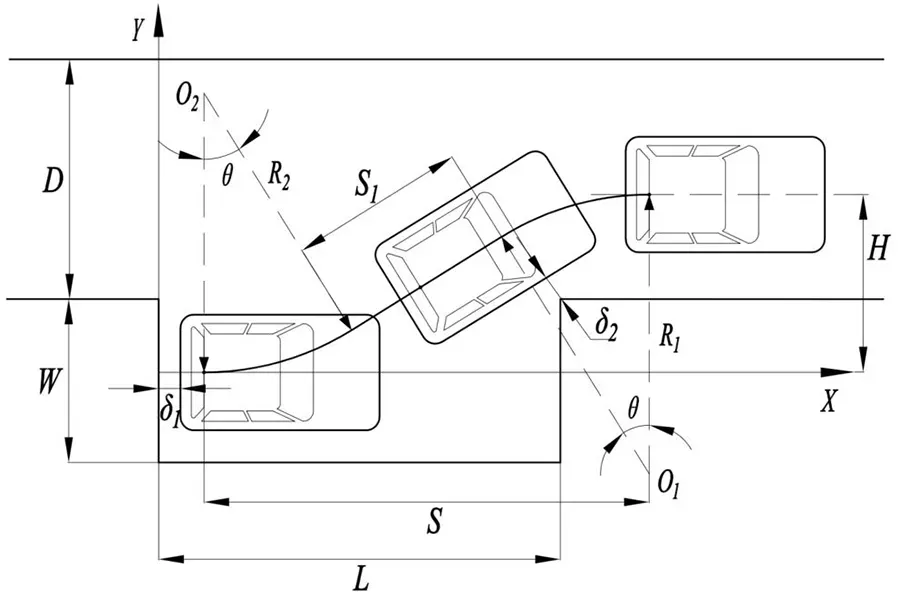
图2 圆弧切直线平行泊车Fig.2 Circular arc tangent straight line parallel parking

图2中L、W分别为车位长、宽，D为当前车道宽度，R1与R2为两段圆弧的半径，S为车辆初始位置到目标点的水平距离，H为初始位置处车辆后轴中心至目标点的垂直距离，θ为圆弧段对应的圆心角。δ1、δ2为安全距离，用于泊车目标点及最小平行泊车位[8]。

根据图2所示，建立其数学模型为：

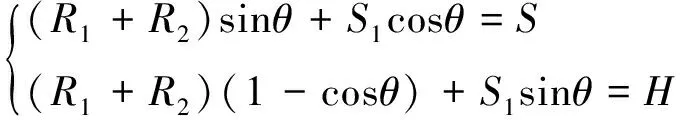
(2)

合并式(2)，可得：

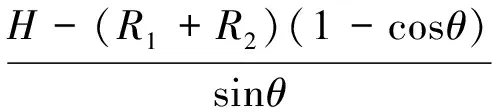
(3)

获取距离S及H后，令半径R1=R2=Rmin，结合式(2)求解参数S1和θ，实现基于最小转弯半径的圆弧切直线平行泊车路径规划。

2.1.2 基于三次样条插值的路径优化

基于几何方法生成的泊车路径存在曲率不连续，因此采用3次样条插值保证路径曲率连续。其定义如下[9]：

假设有n+1个控制点：

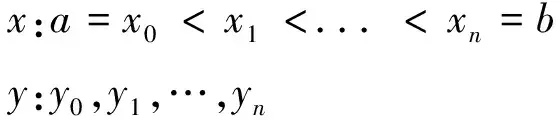
(4)

在单个区间[xi,xi+1]内，三次多项式表示为：

fi(x)=ai+bi(x-xi)+

ci(x-xi)2+di(x-xi)3

(5)

式中,i=0,1,···,n-1，ai、bi、ci、di为待求的4n个未知数。最终求解得到包含n段三次样条曲线的拟合曲线。

2.2 泊车速度规划

针对泊车场景进行速度规划时需满足位姿、距离等约束，故考虑基于最优的方法实现速度规划。本研究提出基于二次规划(quadratic programming，QP)方法进行泊车速度规划[10]。

采用5次多项式曲线作为泊车行驶距离-时间(s-t)曲线表达式，构建最优问题求解曲线系数，其一阶导数即为规划的速度曲线。假设单次规划总时长为T，则s-t曲线表示为：

φ(t)=u0+u1t+u2t2+u3t3+u4t4+u5t5

(6)

式中μi为曲线系数，t∈[0,T]，令：

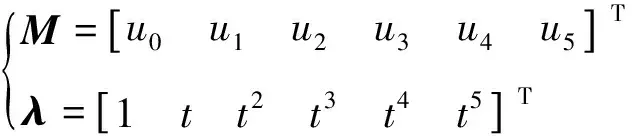
(7)

对式(6)中各未知系数求解即可求得规划时长T内的s-t曲线，一阶求导后即为所需要的最优速度曲线。 求解过程如下：

首先，构建代价函数。

所构建的代价函数表达式为[10]：

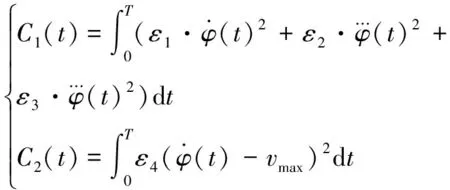
(8)

式中,T为规划总时长，εi(i=1,2,3,4)为权重系数，vmax为泊车过程的最大期望速度。C1项保证舒适性，即速度、加减速、加速度变化率平稳变化；C2项保证时间因素和经济性，即尽可能提高泊车行驶速度。

接着，将上述代价函数转化为标准QP形式：

C(t)=C1(t)+C2(t)=

M-ε4·H4·M

(9)

式中，H1、H2、H3、H4矩阵如下：

最后，设计过程约束。

(1)速度、位置约束

假设规划的泊车路径总距离为S′：

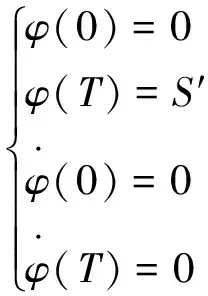
(10)

(2)单调约束

考虑行驶距离s与时间t为单调递增的关系，相邻采样点间应满足：

λi·Mi-λi+1·Mi+1≤0

(11)

(3)最大速度约束

考虑泊车场景限速，考虑最大速度约束：

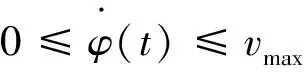
(12)

通过求解上述QP问题可得到最优s-t曲线，对其进行一阶求导后即为规划的速度曲线。该方法中所规划的s-t速度曲线中总时长T可由基于规则的梯形规划算法[11]获取参考值，该方法在此不进行赘述。

3 泊车运动控制

3.1 纵向控制器设计

考虑到车辆具有高度非线性及参数时变特性，这将导致难以建立精确的纵向动力学模型[12]。因此，本研究选用位置式PID控制和基于速度误差直接输出期望油门/制动控制指令[13]。

位置式PID控制的离散化计算公式为[14]：

u(k)=KPe(k)+KI∑e(k)+

KD(e(k)-e(k-1))

(13)

式中，u(k)为期望油门或制动值；e(k)为速度偏差；∑e(k)为偏差累积和；KP、KI、KD分别为驱/制动PID系数。

式(13)的e(k)根据驱/制动模式定义为：

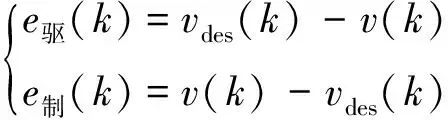
(14)

式中，v(k)为车辆当前速度；vdes(k)为目标点参考速度。

3.2 横向控制器设计

MPC控制是一种滚动求解多约束优化问题的控制方法，鲁棒性较强[15]。本研究采用非线性MPC设计泊车横向控制器。

(1)预测模型

低速泊车场景下无需考虑车辆稳定性等动力学因素，采用运动学模型进行MPC设计在保证较高精度的同时具备复杂度低、实时性高的优点。因此，本研究选用运动学模型作为预测模型并进行离散化处理，同时MPC以控制增量作为待优化变量，离散化后模型为：

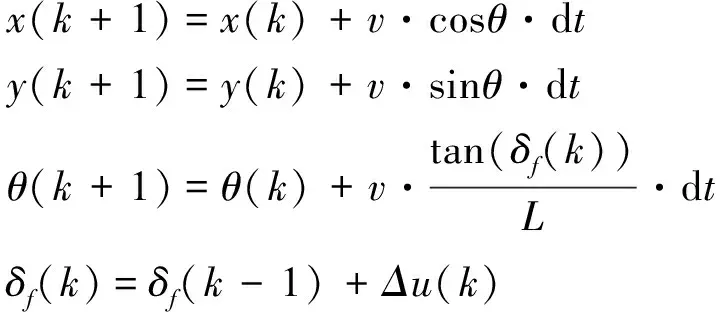
(15)

(2)建立最优控制问题

设计目标函数如下[16]：

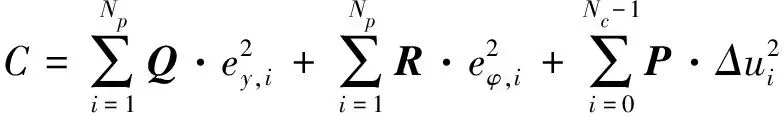
(16)

约束条件：

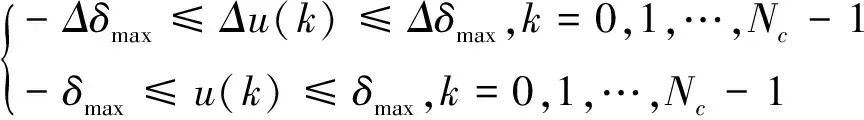
(17)

式中：第一项考虑预测时域内的位置偏差ey，保证其路径跟踪能力；第二项考虑横摆角偏差eφ，保证车辆位姿状态；第三项考虑控制量变化Δu，保证控制平稳。Q、R、P为权重矩阵，Np为预测时域，Nc为控制时域，Δδmax为允许最大前轮转角增量，δmax为允许最大前轮转角。

在每个周期内利用fmincon求解器完成上述最优控制问题求解，得到控制时域Nc内最优控制增量序列：

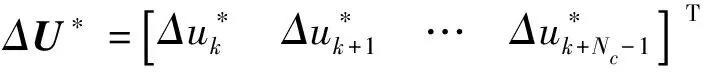
(18)

取式(18)中最优控制增量序列的第一个元素，求得当前时刻最优控制量为：

δ*(k)=δ(k-1)+Δu*(k)

(19)

4 仿真与分析

为验证所提出的针对平行泊车场景的自动泊车系统轨迹规划与运动控制策略，本研究首先基于Matlab对轨迹规划算法进行验证，之后基于Prescan/Simulink搭建平行泊车场景及联合仿真模型，验证轨迹规划到运动控制算法的正确性。仿真所用部分参数见表1。

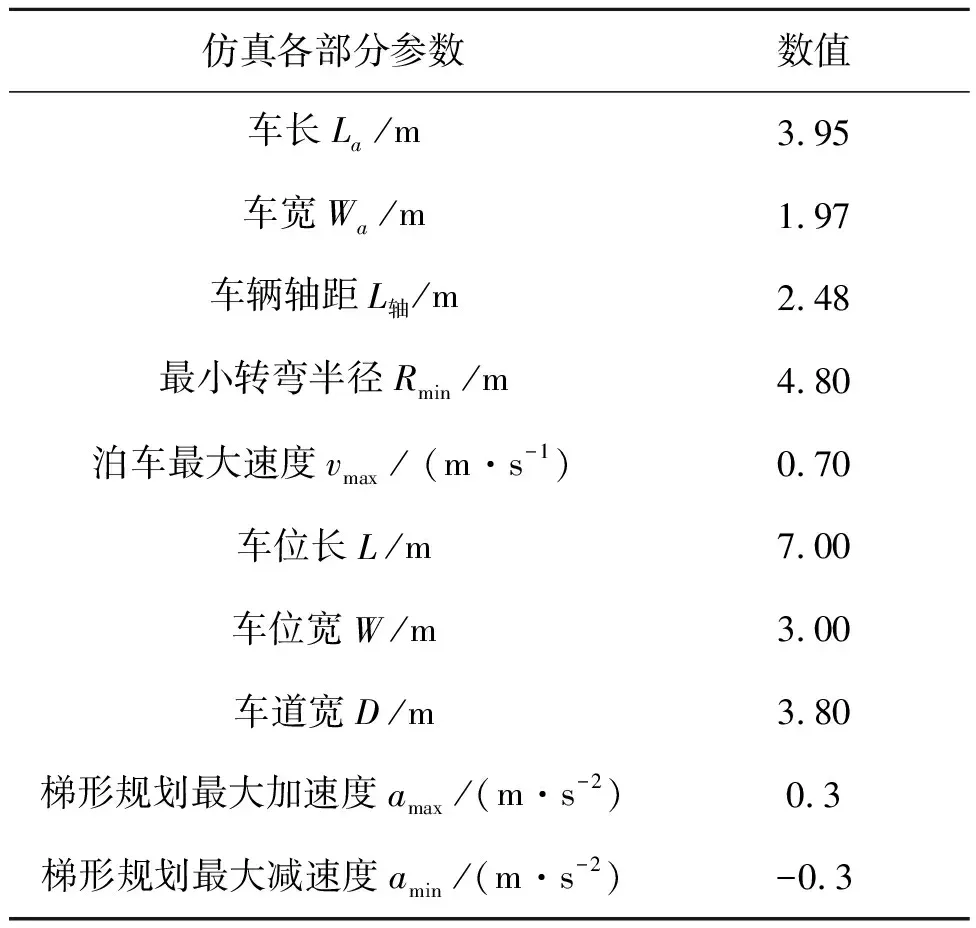
表1 仿真部分参数

4.1 基于Matlab验证平行泊车轨迹规划

假设车辆后轴中心至目标点垂直距离H=1.40 m，至目标停车点的水平距离S=8.30 m。路径规划仿真结果如图3所示。

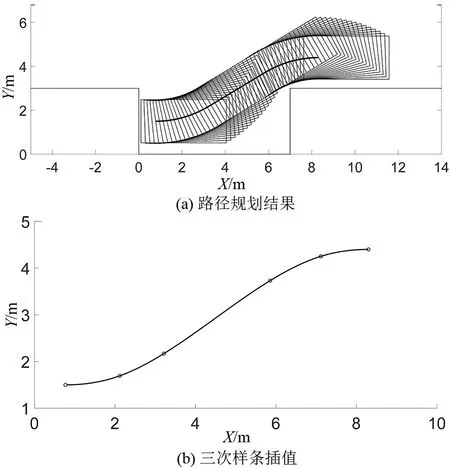
图3 平行泊车路径规划及插值仿真结果Fig.3 Parallel parking path planning and interpolation simulation results

从结果可见，规划的泊车路径满足无碰撞约束，且经过3次样条插值后实现曲率连续。进一步根据上述路径规划结果，计算得到用于QP速度规划的平行泊车总路程S′=8.20 m，同时根据梯形速度规划算法得到用于QP速度规划的s-t曲线总时长T=15 s(向上取整)。利用上述两个条件，基于QP二次规划的速度规划仿真结果如图4所示。

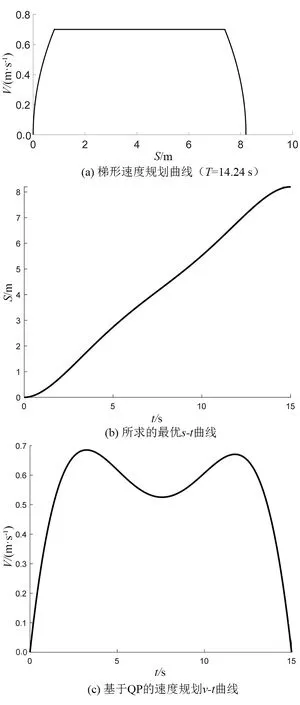
图4 基于QP的最优速度规划仿真结果Fig.4 Simulation results of optimal speed planning based on QP

从图4可以看出，由QP求解的最优泊车速度曲线满足泊车过程的距离、最大速度等约束，同时保证了速度平稳变化。

4.2 基于Prescan/Simulink联合仿真验证

本研究利用Prescan软件建立自动泊车仿真场景，基于Prescan/Simulink联合仿真验证所提的自动泊车规划及控制策略的可行性。所用的仿真参数同表1，给定车辆一侧至停车位边界距离h=1.40 m，联合仿真过程如图5所示。

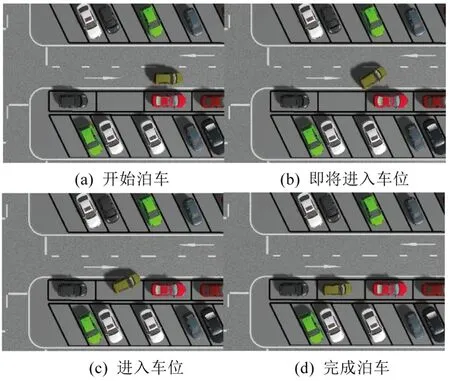
图5 水平泊车整体仿真过程Fig.5 Overall simulation process of horizontal parking

运行时首先基于车辆状态及车位信息规划平行泊车路径，其次计算得到用于QP速度规划的泊车总路程S′=8.60 m以及s-t曲线总时长T=16 s，根据上述两个条件通过QP求解最优速度曲线，最终通过PID及MPC进行控制。结果如图6所示。

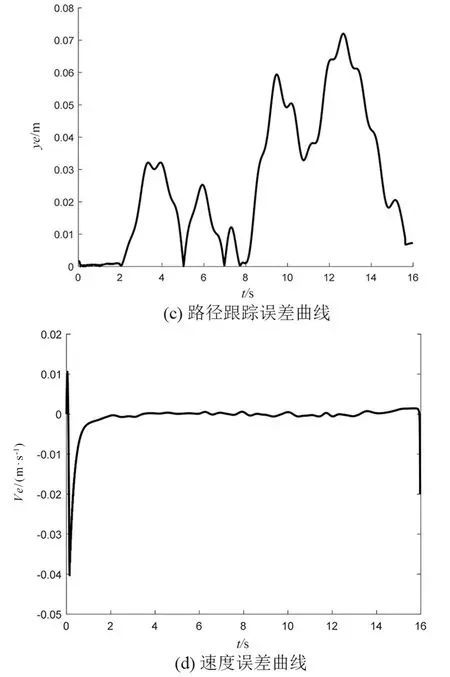
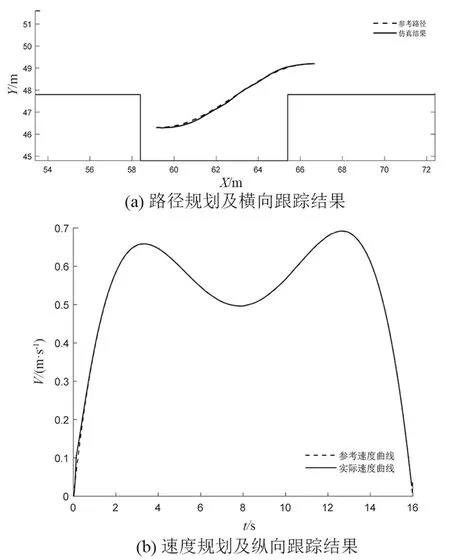
图6 水平泊车轨迹规划及跟踪控制结果Fig.6 Horizontal parking trajectory planning and tracking control results

由Prescan/Simulink联合仿真结果可知：所规划的圆弧切直线平行泊车路径与车位边界无碰撞，速度曲线满足最大速度约束及平滑变化等要求，速度控制过程中最大误差为0.043 m/s，路径跟踪过程最大误差为0.072 m，满足低速泊车控制要求，验证了所提出的平行泊车系统轨迹规划与运动控制策略的可行性。

5 结语

本研究针对平行泊车场景提出了一种完整可行的泊车轨迹规划与运动控制策略，并通过Prescan/Simulink联合仿真平台对所提算法进行了验证，仿真结果表明所提出的平行泊车系统轨迹规划与运动控制策略能够使车辆精确、平稳地泊入平行车位，对于平行泊车系统设计具有一定的参考意义。