基于混合特征选择算法的抑郁症分类方法
王 玥 沈潇童 王苏弘 陈芋圻 邹 凌*
1(常州大学信息科学与工程学院 江苏 常州 213164) 2(常州市生物医学信息技术重点实验室 江苏 常州 213164) 3(苏州大学附属第三医院 江苏 常州 213164)
0 引 言
抑郁症是一种精神疾病,患者会表现出失去兴趣、自卑感和注意力不集中等相关的精神症状,甚至会出现自杀倾向[1]。根据世界卫生组织报告,预计在2030年,抑郁症将成为世界疾病负担的首位。目前,临床对抑郁症的诊断主要是通过临床访谈和量表对症状进行评估,如果根据大脑生理机制的情况监测到抑郁症的出现,不仅能够使治疗更加有效,也更利于医生改善患者的心理健康状态[2]。而脑电(EEG)被公认为是一种廉价、安全且无创性地评估脑功能的方法,更加适合于常规使用[3]。
此前,脑功能连接已被广泛应用于识别有无抑郁症的差异,并根据这些差异进行分类。Peng等[4]使用相位滞后指数研究抑郁症患者的脑功能连接,并将上三角矩阵的连接值提取作为特征进行分类。Zhong等[5]通过计算全脑功能连接,使用矩阵的连接值作为特征对抑郁症和健康对照进行分类,结果表明分类精度达到90%以上。Liu等[6]将脑功能计算后的连接值作为进一步分析的特征并进行分类。
由于特征维数较大,为提高学习算法效率,特征选择显得尤为重要。Sayed等[7]提出混沌乌鸦搜索算法(CCSA),并将其运用于优化20个基准数据集的特征选择问题,结果表明该算法能够找到最佳特征子集从而达到最大的分类性能。Majdi等[8]提出将鲸鱼优化算法(WOA)与模拟退火算法(SA)相结合,使用18个标准数据集对该方法进行评估,发现其能使用更少的特征而获得更高的准确性。Shen等[9]为解决高维特征选择问题,提出了竞争群优化器算法(CSO),并与标准的蚁群算法(PSO)和最新PSO变体算法相比,其选择的数量不仅最少,还能获得更好的分类性能。本文选择了二次规划特征选择(QPFS)和费舍尔分数,QPFS是依据互信息方法获取同类之间的相关性,且对于大型数据集有着较高的效率,而费舍尔分数排序是基于相似性方法,根据同一样本中特征值相似,而不同样本中的特征值不同来进行排序。
机器学习在分类模型训练和建立中有着广泛的应用。Schnyer等[10]通过脑白质MRI指标,使用机器学习中的SVM进行分类预测,发现仅使用大脑右半球的分类精度更高。Sharma等[11]将所采集的脑电信号分解为七个小波子带(WSB),六个详细的WSB和一个近似WSB的L2范数的对数作为特征,通过最小二层支持向量机进行分类,模型分类精度高达99.58%。Li等[12]采取了抑郁症患者和健康人的任务态数据,将功率谱密度、近似熵等18种脑电特征提取出来,利用差分进化的全局优化性能获得最佳特征值,再使用K近邻进行分类,精度最高可达98.33%。
本文采用了EGI公司的64导脑电采集系统,结合Net station软件,实时采集了抑郁症患者和健康人在面对flanker范式下的脑电信号,对其预处理分段,采用相位锁定值构建脑功能网络,求得连接矩阵,将两组被试者具有显著性差异的连接值作为分类特征进行提取,然后使用二次规划特征选择方法(QPFS)和费舍尔分数分别对特征进行选择排序,结合二者优点,根据文献[13]研究结果和排序结果,选择排序后的前100个特征集,取二者交集和并集。进一步使用遗传算法(GA)选择出最佳子集,因为GA是一种简单的算法,且已自1970年以来被广泛使用,被证明在减少特征维度和提高分类精度方面十分有用。最后采用支持向量机(SVM)、K近邻(KNN)和逻辑回归(LG)分类器,为了尽可能地利用数据,分类器采用留一交叉验证法,结果表明,采用混合算法的交集联合遗传算法,特征数目从1 317降维至12,且分类精度也达到最高值96.8%。
1 方 法
1.1 被 试
本次共16名健康青少年(对照组)与15名患有中度抑郁症(抑郁组)的青少年参加实验,其年龄范围为(16.31±1.25),两组之间的年龄无统计意义。所有被试者均无精神病史、吸毒史和酗酒等情况,且皆为右利手,其在常州市第一人民医院经过临床确诊,通过汉密尔顿抑郁量表检测,结果显示,抑郁组的分数高于对照组。
该实验已经常州市第一人民医院伦理委员会批准,所有受试者与其监护人均签署了知情同意书,自愿参加本实验。
1.2 实验范式
该实验使用E-prime软件进行。首先,屏幕上将会出现形如“+”的注视点,持续时间为200~700 ms,随即出现一幅由5个箭头组成的图形,目标刺激为中间箭头,如下所示,“<<<<<”(一致方向)、“>>>>>”(一致方向)、“<<><<”(不一致方向)、“>><>>”(不一致方向),该刺激持续时间为200 ms。最后,屏幕将会出现全黑图片,被试者需要在1 700 ms内根据目标刺激与两翼箭头的方向按下按钮,其中,目标刺激与两翼箭头一致时按下“1”键,目标刺激与两翼箭头不一致时按下“4”键。在正式实验开始前,将会有一个训练部分,该部分有32试次。正式实验阶段有11部分,每部分同样有32试次。一致和不一致图片以伪随机的方式呈现,出现概率相同,具体如图1所示。
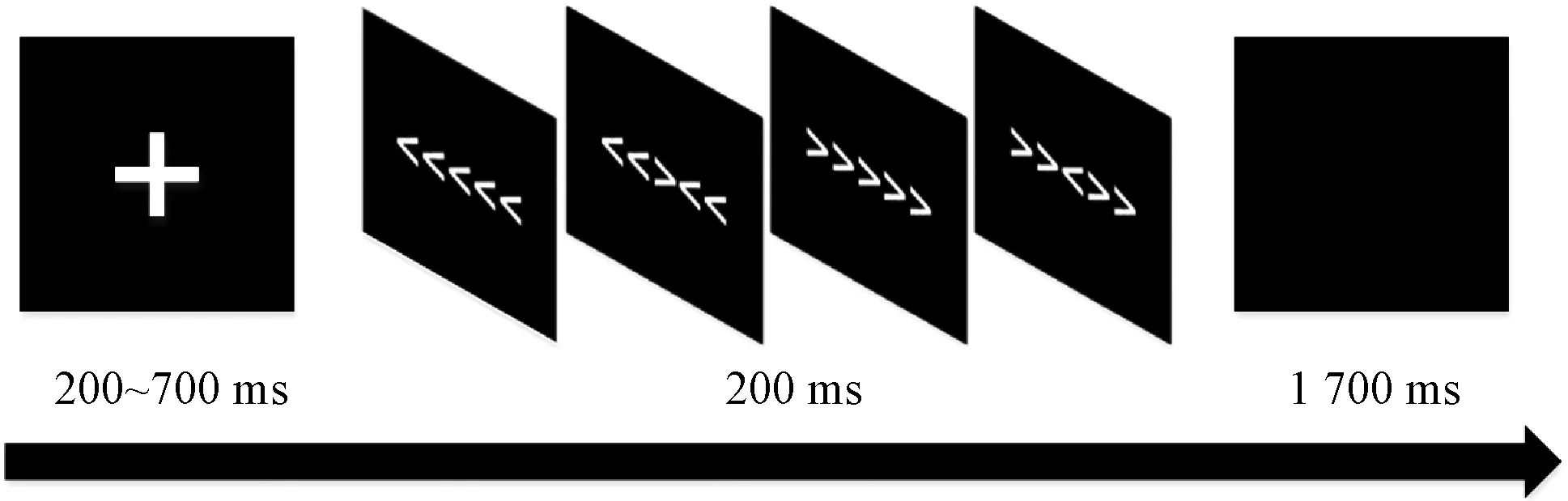
图1 flanker范式流程示意图
1.3 数据采集及预处理
本次实验使用软件Net Station与EGI公司的64导联脑电采集系统实时采集,电极位置分布符合10-10国际标准,且以Cz为参考电极,采样频率为500 Hz,电极阻抗均设定在50 kΩ以下,进行0.5~45 Hz的带通滤波。
原始脑电信号的预处理使用EEGLAB(版本号:v14.1.2)工具箱[14],其经过0.5~45 Hz高低通滤波,并针对所有导联进行独立成分分析(ICA),用以消除眨眼、头动等伪迹[15-16]。对于信号漂移的坏导,使用相邻导联数据叠加平均替换,且参考点重新转换为平均参考。基线重新校正为刺激前200 ms,并根据刺激前200 ms至刺激后800 ms对数据进行分段。
1.4 脑功能连接
相位锁定值是检测两个信号在具体频率范围内与幅度无关的瞬时锁相值,以此量化信号间的相互作用[17]。给定信号x,在进行带通滤波后,其相位瞬时相位可以通过计算希尔伯特变换获得[18-19]:
(1)
式中:φ的取值范围为-π到π。z(t)根据x(t)经过下式计算得到:
z(t)=x(t)+i·HT{x(t)}=A(t)·ei·φ(t)
(2)
在t时刻的相位锁定值定义如下:
(3)
式中:N代表的试次的数量;θ(t,n)代表两个信号的瞬时相位差,即φ1(t,n)-φ2(t,n)。在此,PLV的取值介于0~1范围内,当两信号在该试次的相位完美同步时,PLV的取值为1,反之,取值则为0。
根据式(3),本文研究了在五个频段下被试者的脑功能连接,分别为delta(1~3 Hz)、theta(4~8 Hz)、alpha(8~13 Hz)、beta(13~30 Hz)和gamma(30~45 Hz)[20]。并使用t检验寻找对照组和抑郁组在面对两种情况下脑功能连接的显著差异,将差异显著的连接值作为原始特征。
1.5 基于全局互信息的二次规划特征选择
特征选择是一种必不可少的处理步骤,它能有效地消除机器学习样本中不相关或者冗余的特征,进而提高计算效率。本文特征选择方法流程图如图2所示。
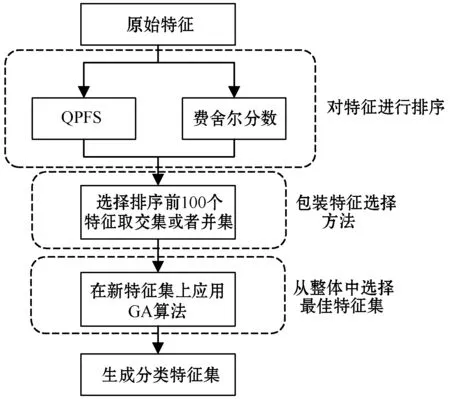
图2 所提出的混合特征选择算法流程
基于互信息的方法则在数据挖掘中的重要特征选择有着重要地位。为了避免做出次优选择,可将基于互信息(MI)的特征选择作为全局优化问题,同时,考虑所有特征之间的相互作用来做出全局决策。假设有m个样本n个特征,QPFS公式如下所示:
(4)
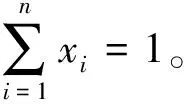
1.6 费舍尔分数
在本研究中,除了基于二次规划特征选择将特征进行排序,还选择使用费舍尔分数对特征进行选择。费舍尔分数根据Fisher准则对每个特征进行评分,第j个特征的费舍尔分数可通过以下公式计算得出:
(5)
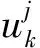
1.7 混合特征算法
设原特征集为f={f1,f2,…,fn}m×n,代表着有m个样本,n个特征。经过QPFS按照权重进行排序后,得到fQPFS={fQ1,fQ2,…,fQn},此外,根据费舍尔分数进行排序,得到ffisher={fF1,fF2,…,fFn},为了联合两种算法,尽可能的结合二者优点,分别对fQPFS和ffisher特征集中,前100个特征取交集或并集:
f交集={fQ1,fQ2,…,fQ100}∩{fF1,fF2,…,fF100}
(6)
f并集={fQ1,fQ2,…,fQ100}∪{fF1,fF2,…,fF100}
(7)
1.8 遗传算法
使用混合特征算法以后,再使用遗传算法进一步选择合适的特征子集,如图2所示。遗传算法是基于达尔文的自然进化和选择过程的随机过程搜索算法。通过模拟生物学中的繁殖、交叉和突变现象,在不断的迭代中选择出更好的个体[21]。首先,随机初始化种群,即父本,计算适应度函数以后,当满足目标条件时,该算法结束,否则将会根据适应度选择父本,根据父本的染色体,进行交叉产生新的子代,子代进行变异,根据交叉和变异生成了新的种群,计算该种群的适应度函数,直至其满足目标条件。考虑到操作的快捷和计算效率,且由于特征值均在0~1之间,编码采用二进制编码,设置特征值小于0.5为0,大于0.5为1。另外,考虑到分类性能,选取了较为广泛使用的基于近邻法分类的适应度函数,用以计算预期的适应度,进一步评估染色体的准确性。
1.9 分 类
机器学习中包含着多种分类器,SVM、KNN和LG将会被使用来支持算法结果。为了分类精度更加可靠和最大化利用数据,此次分类采用留一交叉验证法,将平均后的分类精度(ACC)作为分类结果,其参数计算如下:
(8)
式中:TP代表正确将抑郁组识别为抑郁组的数量;TN表示正确地将对照组识别为对照组的数量;FP代表错误地将抑郁组识别为对照组的数量;FN表示错误地将对照组识别为抑郁组的情况。
2 实 验
2.1 功能连接
根据PLV方法计算所得,抑郁组与对照组的在五个频段下的功能连接矩阵图(64×64,代表导联×导联)如图3所示。该连接矩阵的连接值介于0到1,连接值越大,代表两信号间的同步性越强。从图中可以看出,抑郁组的连接强度在五个频段下都较低于对照组,然而对比在五个频段下,抑郁组和对照组在面对两种情况时,抑郁症患者在对角线处的连接强度高于对照组,而除对角线以外,抑郁症患者的连接强度低于对照组。

图3 五个频段下受试者的脑功能连接图
为了寻找抑郁组与对照组在面对一致刺激和不一致刺激的显著差异,将抑郁组与对照组进行t检验,提取p<0.05的连接值,如图4所示。通过抑郁组与对照组的连接强度差异来看,相对于面对箭头一致的刺激,面对不一致刺激时,抑郁组与对照组的差异更为显著,且在五个频段下,均有较多差异显著的连接值。

图4 五个频段下抑郁组与对照组的显著差异图
2.2 特征排序
在提取五个频段和两种情况下的连接强度的显著性差异作为原始特征,特征数共1 317个,分别根据QPFS和费舍尔分数进行特征排序,QPFS排序后结果如图5所示。前100个特征权重已达整体权重的99.99%,因此,分别取QPFS和费舍尔分数排序后的前100个特征进行交集和并集,生成新的特征集。
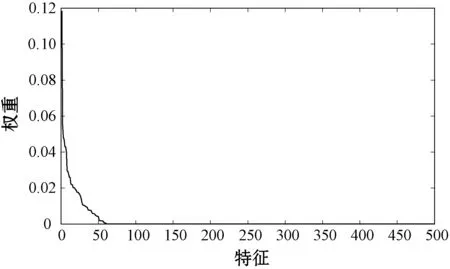
图5 QPFS排序后的特征权重
2.3 分类结果
在分别对QPFS和费舍尔分数排序过后的前100特征,分别对两个新特征集进行并集和交集,再使用GA算法,进一步确定最优的分类特征集。同时,为了显示该操作的优越性,分别在QPFS和费舍尔分数排序后的前100特征进行GA算法生成新子集,并采用SVM、KNN和LG进行分类,其特征数和分类结果如表1所示。
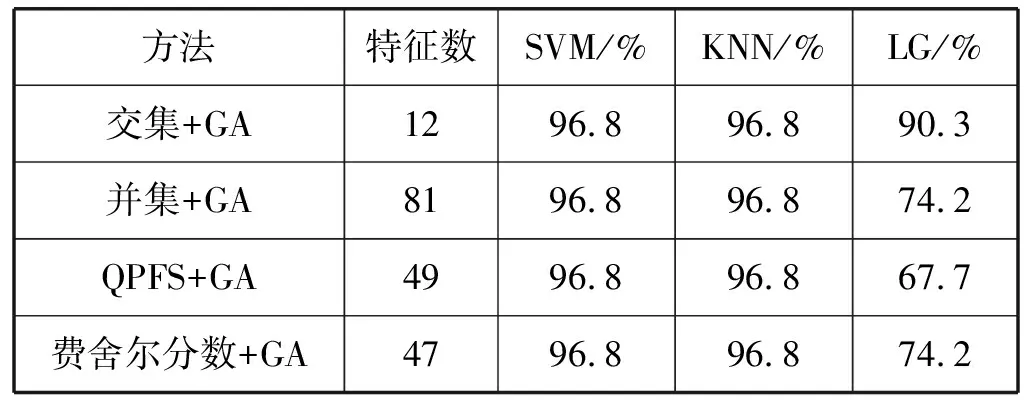
表1 不同算法下所使用的特征数和分类精度
当采用SVM和KNN分类器时,其分类精度都能达到最高,但是,选择QPFS和费舍尔分数的交集结合GA,其特征数目最少,在仅有12个特征的情况下,精度都能达到96.8%。
为了进一步突出所提算法的优越性,将其与经典的特征降维算法进行比较分析,其中包括主成分分析(PCA)、线性判别式分析(LDA)、等距特征映射(ISOMAP)和局部线性嵌入(LLE)。其中,LDA、ISOMAP和LLE使用了drtoolbox工具箱,先对1 317个特征使用最大似然估计(EKM)做本质维度估计,再调用不同函数进行降维;而PCA降维采用MATLAB中的princomp函数直接对1317个特征降维。将所有降维后的特征值分别进行分类,结果如表2所示。
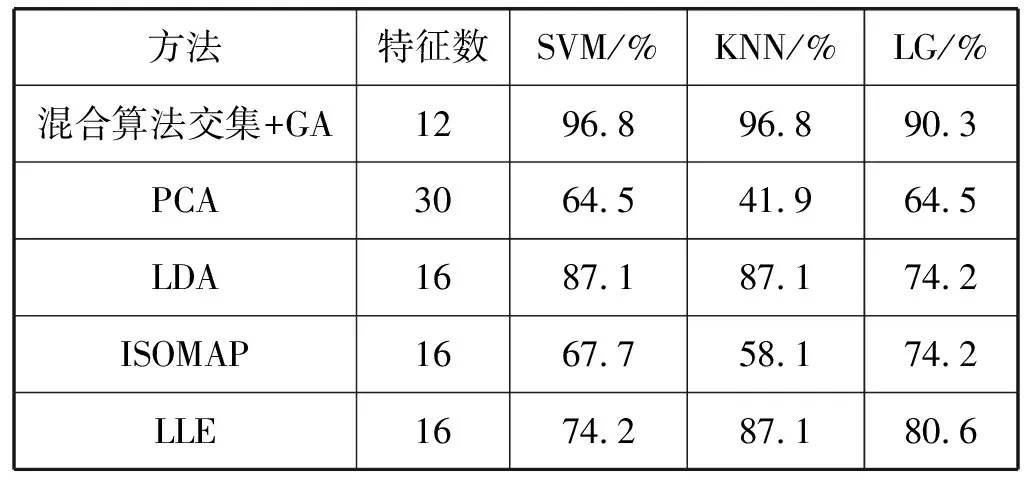
表2 经典算法下所使用的特征数和分类精度
与传统经典算法相比,多算法交集联合GA所提取出的特征子集,不仅分类精度更高,特征数目也更少。
3 结 语
本研究采用了flanker任务态范式来研究抑郁组与对照组之间的差异,在分析面对一致性刺激和不一致刺激时的脑功能连接状态时,运用了相位锁定指数构建脑功能连接网络。研究发现,在对角线区域,抑郁组的脑功能强度大于对照组,但是在其他区域,抑郁组的脑功能强度低于对照组。另外,在面对一致性刺激和不一致刺激时,将两组差异显著的连接值作为特征进行分类,但是特征数量较大,如果直接进行分类则计算耗时较长,效率较低。
本文着重于在保证分类精度的情况下,如何选出特征数目更少的分类特征子集。首先,使用基于互信息的QPFS对所有特征根据其权重进行排序,取其前100个特征作为新特征集,另外,对原始特征集使用费舍尔分数同样进行排序,也取前100个特征作为新特征集。QPFS能够有效地根据互信息选择出特征间相关性较大的特征,从而筛选出有效特征,而费舍尔分数根据同类样本间的相似度和不同样本间的差异度选择出分类特征。对于两个特征集,分别取其并集和交集,取交集或并集的目的是为了满足所选子集具有两种算法的优点。然后使用GA进一步优化特征子集,作为最终的分类特征集。最后在分类时,分别采用SVM、KNN和LG多种分类器,结果表明,多算法交集联合GA在特征精度同样的情况下,拥有更少的特征数;与广泛使用的传统PCA、LDA、ISOPMAP和LLE相比,其不管在分类精度,还是特征数目方面,都显示出了更优越的性能。
本文方法偏重于特征选择和降维,作为计算机辅助诊断技术来说是可行的,大大降低了临床诊断时间。同时,对于高维特征选择的问题,本文研究也提供了一定的思路,从1 317个高维特征数降到仅12个特征。
后续将进一步划分脑区作继续研究,由脑功能连接矩阵图可以看出,两组都有较为明显的脑区,单独从脑区进行分析,提取特征参数,将进一步提高计算机辅助诊断的可行性。

