基于超立方体拓扑结构的NoC测试规划研究

胡 聪 信文雪 周 甜 朱爱军 许川佩

1(桂林电子科技大学电子工程与自动化学院 广西 桂林 541004) 2(桂林航天工业学院电子信息与自动化学院 广西 桂林 541004) 3(广西自动检测技术与仪器重点实验室 广西 桂林 541004)

0 引 言

片上网络(Network on Chip,NoC)结构作为一种高度集成的片上多处理器系统[1]，虽然打破了传统片上系统(System on Chip,SoC)结构的性能瓶颈，但是，单位面积上芯片IP核(Intellectual Property core)数目的增长以及芯片结构复杂度的攀升，将会对芯片的测试效率带来新一轮的考验。因此，以缩减测试成本为目标，考虑软硬件等多种约束条件的限制，如何实施高效的并行传输与测试，成为一个NP难题，同时也具有较大研究价值。

为此大量学者在NoC测试方面做了诸多研究。文献[2]提出一种基于模糊逻辑的任务映射方法，可根据芯片需求调整任务映射权重因子，有效降低通信延时、功耗以及芯片测试核的最高温度。文献[3]提出了一种新的元启发式算法——差分灰狼算法。通过对元启发式算法进行改进，有效降低了测试过程中的时间和经济成本。文献[4]针对非全互连类型的3D NoC,提出一种能够自适应调整路由路径的混合多播算法，在同一平面内与不同平面之间分别通过使用Hamilton图与树结构的多播思想进行路径选择,保证了数据在高效传输过程中不会失真。文献[5]为了减少测试时间，提出了xy方向连接子图划分方法来消除测试前的路径冲突，同时确定了测试访问点的位置。综上所述，目前的研究虽然对测试过程中的功耗和时间进行了不同程度的优化，但所选拓扑结构仅处于二维和三维阶段。

针对上述文献的不足，本文提出了一种基于超立方体拓扑结构的NoC测试规划方法。从NoC测试规划的拓扑结构方面进行考虑，提出采用在平均延时、网络直径以及功耗等方面都优于3D Mesh结构的超立方体拓扑结构对NoC测试规划进行研究；在测试规划中针对该拓扑结构设计了具有部分自适应能力的E-cube路由算法，减少了测试过程中的路由传输时间；本文采用的优化算法为改进的PSO，增强了PSO的全局寻优能力与局部精细搜索能力，实现了NoC测试规划问题的优化求解。

1 NoC测试基本概念

1.1 超立方体拓扑结构

拓扑结构决定了NoC中IP核、路由器以及通信链路之间的连接方式，很大程度上决定了系统的性能和代价。3D Mesh结构因其对称性好、可扩展性强、简单易实现、布局规整等特点，目前在片上网络研究中被广泛采用，但是它仍具有平均延时长和网络直径大等缺点。超立方体拓扑结构不仅具有对称性好、可扩展性强等特点，而且其网络直径短,因此本文选择超立方体结构对片上网络进行研究。

为降低测试硬件开销、减少测试时间，本文复用NoC作为测试访问机制(test access mechanism,TAM)，采用并行测试的方式对各个IP核进行测试。并行测试虽然加快了测试时间，但容易造成过热测试和损坏芯片等问题。因此本文通过添加子立方体功耗和总功耗双重约束来减少测试过程中由于功耗过高而产生的一系列故障问题。

本文研究的NoC测试规划问题可简要概述为：对于一个NoC，已知N个IP核的相关参数如：扫描链长度及数量和测试矢量个数等，以及带宽数目、TAM条数、拓扑结构、调度方式和路由算法等。研究在测试资源无冲突、功耗满足限制的条件下，如何通过群智能优化算法求得最佳测试方案。

1.2 目标函数与测试约束函数条件

1.2.1目标函数

测试调度以系统测试时间为目标函数，系统测试时间取决于测试时间最长的一条TAM，计算公式如下：

(1)

式中：B代表TAM条数；k代表第b条TAM上的IP核个数；Ttesti代表IP核i的测试时间，包含对IP核自身进行测试所耗费的时长及测试数据包的路由时长。

1.2.2功耗约束

测试功耗与测试时间存在互为代价的关系，虽然并行测试的方式有效缩短了测试时间，但同时也导致测试功耗的上升。本文对拓扑结构中的两个子立方体功耗与超立方体结构的总功耗进行双层约束。

(1) 在任意的时间槽t，任一子立方体中在测核的功耗总和Pl需要满足：

(2)

式中：Ptesti(l)表示某一时刻分布在子立方体结构中核i的总功耗；h表示子立方体结构中被测核数目；Pmax-subcube(l)为子立方体结构的最大允许功耗。

(2) 在任意时间槽t，要求拓扑结构中所有正在进行测试的IP核的功耗之和Ptotal必须低于总功耗的上限Pmax。

(3)

式中：Ptotal为某一时刻超立方体结构中的总功耗；L表示超立方体结构中子立方体的个数；Ptest(l)为子立方体中IP核的测试功耗；Pmax为允许最大总功耗。

2 NoC测试规划中的超立方体拓扑结构

2.1 超立方体拓扑结构

超立方体网络结构[7]具有网络直径小、连通性高、网络寻径路由简单等优点，很早便被提出并进行研究。图1对四维超立方体网络的定义与节点的编号方式均参考文献[7]。

图1 四维超立方体网络及结点编号

本文对N维超立方体结构与网络规模为M×N×L(N>M>K>1)的3D Mesh和3D Torus结构进行了相关参数比较。由表1可知超立方体结构不仅比其他两种结构拥有更多的物理链路数而且其网络直径比3D Mesh结构更短，且对于超立方体结构维数越高，对比优势越明显。

表1 超立方体结构与经典结构性能指标对比

2.2 具有部分自适应能力的E-cube路由算法

E-cube路由算法是一种确定性路由算法，不能根据网络状态进行动态调整，缺乏自适应性。本文提出了能根据网络当前状态进行适度调整的具有部分自适应能力的E-cube路由算法。

区别于确定性路由算法，本文所提算法采用低维优先原则，通过设定输出端口的优先级控制数据输出。在数据传输过程中，首先判断初始节点是否与目标节点相同，若相同则将测试数据传至此节点所在IP核，否则判断下一跳节点中的1维方向是否被占用，如果未被占用，则向此节点传输，反之，则判断下一跳节点的2维方向。以此类推，逐次向高维传输。这样可以避免确定性路由算法某一维由于受到阻塞而带来的死锁问题。具体过程如图2所示。

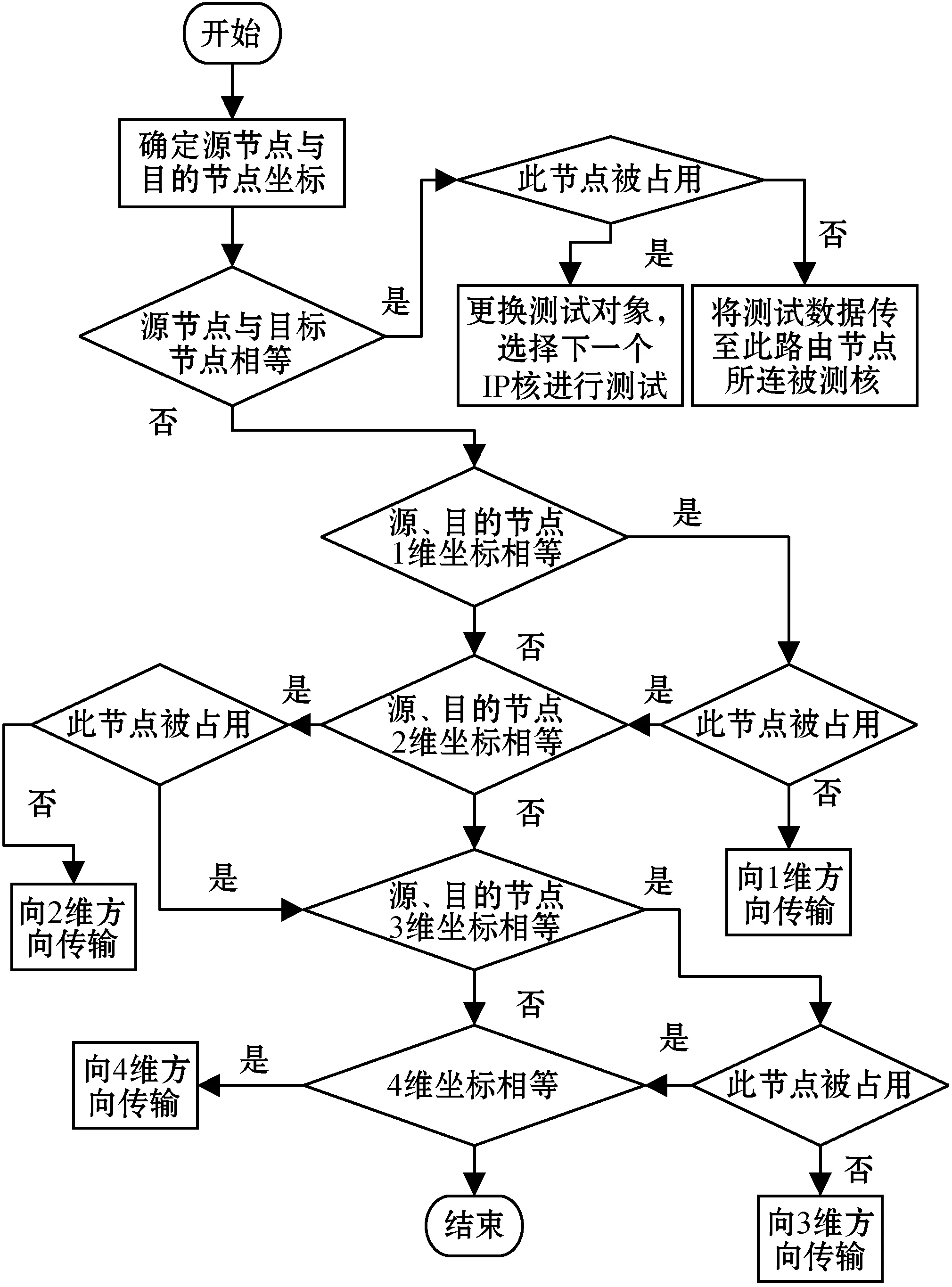
图2 E-cube部分自适应路由算法流程

根据图2所示路由算法，本文以具有16个路由节点的四维超立方体结构与具有相同网络规模2×2×4的3D Mesh结构为例进行对比分析。图3和图4中黑色圆球分别代表输入端口和待测核,黑色箭头所示部分代表路由算法所走路径。由对比可知，图3测试过程中经过的路由器个数及链路条数明显低于图4，且对于超立方体结构，维数越高，优化效果越明显。

图3 四维超立方体拓扑结构

图4 2×2×4 3D Mesh结构

3 NoC测试规基于改进粒子群算法的片上网络IP核测试优化方法

3.1 粒子群算法原理

粒子群算法(PSO)是由Kennedy博士和Eberhart博士提出的一种群体智能进化算法。本文针对NoC测试规划问题，首先利用PSO的随机解对一群随机粒子进行初始化，然后粒子在每次的迭代求解过程中，通过跟踪个体极值pbesti和群体极值gbesti不断地更新自己的速度和位置。对于每一代个体，在找到两个最优值时，粒子根据如下公式来更新自己的速度和位置：

(4)

(5)

3.2 算法设计

PSO具有记忆性且操作简单、搜索能力强、没有交叉和变异运算，但该算法容易陷入局部最优，且缺乏速度的动态调整。针对PSO种群多样性不足导致的早熟收敛和由于迭代后期吸引力过大导致的粒子收敛速度变慢等现象，本文对粒子群算法进行如下改进：

(1) 混沌优化算法更新准则。基于混沌的随机、遍历特性，通过混沌序列而非随机函数产生初始粒子种群，可以使初始种群中的个体具备混沌序列的随机性与遍历性。本文采用的混沌模型为立方映射[7]，如下：

y(n+1)=4y(n)3-3y(n)

(6)

式中：y(n)∈[-1,1]，且y(n)≠0，n=0,1,…。

(2) 学习因子自适应调整。学习因子c1、c2具有自我总结和向优秀个体学习的能力。c1、c2较小时，使粒子在远离目标区域内徘徊，反之，可使粒子迅速向目标区域移动，甚至超过目标区域。为了平衡粒子之间的信息交互能力，得到较好的收敛效果，需要对c1、c2进行动态更新，更新公式如下：

c1=1.0-iter/itermax

(7)

c2=1-c1

(8) (3) 添加压缩因子。由式(4)可以看出，粒子飞行速度与w相关。w越大，粒子飞行速度越大。虽然较大的w有利于跳出局部最小值，便于全局搜索，但易出现“早熟收敛”现象；w越小，则越利于局部搜索。本文提出添加压缩因子φ的方法，对w进行改进。

(9)

(10)

令C>4,C=c1+c2。φ较w而言，不仅可以更加有效地控制和约束微粒的飞行速度，而且也增强了算法的局部搜索能力。

本文根据NoC测试，通过改进粒子群算法可以高效准确地寻找出测试过程中测试时间最短与测试功耗最低的最优解。首先采用映射规则，将每一子立方体拓扑结构中分配的IP核自身的测试时间、测试功耗之和大致相等。其次通过混沌优化算法增加各个IP核分配至多条TAM上的种群多样性。最后在最优解的查询过程中添加学习因子与压缩因子增强算法的搜索能力，减少搜索时间。

改进PSO流程如图5所示，主要包括：对种群进行初始化、适应度值的计算、pbest与gbest的更新、自适应参数的调整等。具体算法流程如下：

1) 初始化粒子种群。利用混沌优化算法对IP核的测试数据分配TAM，产生初始种群。

2) 适应度值计算。各粒子的测试时间由式(1)得出，通过比较找到当前最优值。

3) 更新粒子历史最优pbest与全局最优gbest。

4) 自适应参数调整。

(1) 利用式(7)和式(8)完成学习因子的自适应调整。

(2) 利用式(9)和式(10)完成压缩因子的自适应调整。

5) 检查是否达到终止条件，若达到则结束算法，得出结果，否则转步骤2)。

图5 算法流程

4 实验与结果分析

为验证本论文所提方法的有效性，选取ITC’02国际标准电路中的d695和g1023进行仿真实验。分别将两个电路中的IP核映射至2×2×2×2的四维超立方体结构中。遵循的映射规则为：使每一子立方体拓扑结构中安排的IP核自身的测试时间、测试功耗之和大约相等，如表2所示。在Visual Studio 2019中编译代码。

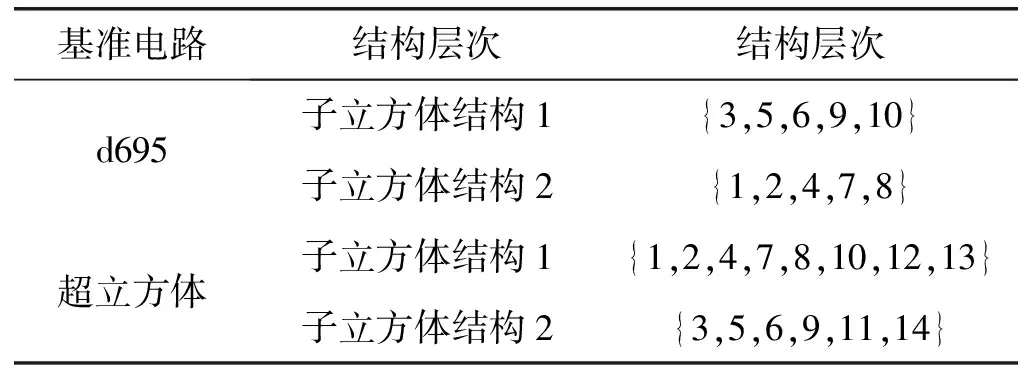
表2 基准电路中核的分布

本文以d695电路为例，画出其测试过程中的Gantt图。图6所示为d695电路在带宽32，功耗约束满足50%条件下的最优测试规划结果图。横轴表示IP核测试的时间历程，可以非常直观地看出每个IP核测试的起止时间，纵轴代表不同的TAM。由图可知，测试开始时，核6、5、4分别在3条TAM上并行测试，在6238时间节点处，TAM2上的5号IP核测试完毕，但此时由于路径冲突或者不满足功耗约束条件，3号IP核的测试数据包无法进行传输，需等待直至测试资源空闲或满足功耗约束条件时才能继续进行测试。

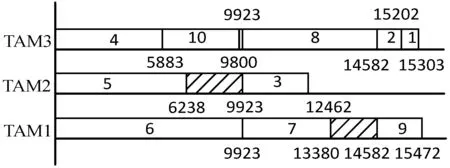
图6 d695电路的测试调度结果

同等条件下，为了进一步验证测试结果，表3对本文所提方法与前人文献中的测试结果进行了对比，结果表明：两条TAM时，本文最高优化率可达16.44%；三条TAM时，本文最高优化率可达17.38%，整体优化率维持在5.42%～17.38%之间。

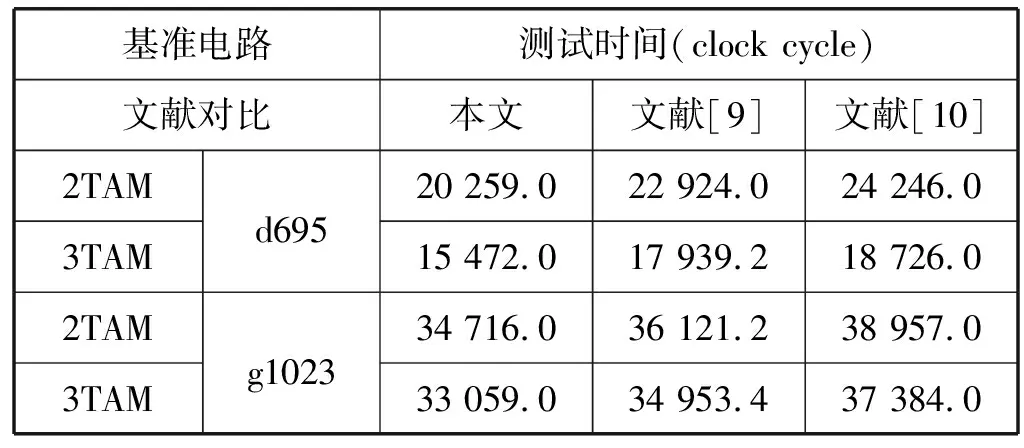
表3 不同TAM条数的优化方法性能对比

5 结 语

本文对NoC测试规划问题进行了研究，提出了一种基于超立方体拓扑结构的NoC测试规划方法。该方法首先通过映射算法将多个IP核分配到超立方体拓扑结构中，采用具有部分自适应能力的E-cube路由算法对IP核进行调度测试。为了对各种测试结果进行高效寻优，本文对PSO进行了三处改进，即引入混度序列增加初始种群的随机性与遍历性、添加自适应调整的学习因子及引入压缩因子对粒子群算法进行改进，增加种群的多样性。用两个标准电路d695与g1023对该方法做了测试，并将实验结果与其他测试方法的实验结果进行比较,结果显示本文测试方法在测试时间与程序运行时间方面都展现出较明显的优势。