基于FD-NOMA的无人机通信系统容量分析*

牛春雨，贾向东,2，曹胜男，万妮妮

(1.西北师范大学计算机科学与工程学院,甘肃 兰州 730070；2.南京邮电大学江苏省无线通信重点实验室,江苏 南京 210003)

1 引言

无人机UAV(Unmanned Aerial Vehicle,)由于其机动性、灵活性的优点，近年来受到了广泛的研究关注[1,2]。与传统的固定基站BS(Base Station)相比，利用UAV作为空中BS为地面用户GU(Ground User)提供通信服务可以极大地提高通信性能，如更高的数据速率和更广的覆盖范围[3]。与传统的空对地无线通信相比，UAV可根据需要快速调整部署，具有完全可控机动性，因此在信息对抗、空中火力制衡与打击、重大灾害近空检测、人员搜救和应急空投等领域具有广阔的应用前景[4 - 6]。近年来，许多学者对UAV通信进行了大量的研究，较多文献表明，部署一个或多个固定UAV可以提高网络容量和覆盖范围[7 - 9]，通过缩短UAV与GU的距离，可以提高通信性能。文献[10]研究了UAV辅助通信的数据采集问题，通过联合优化传感器节点和UAV飞行轨迹，调整UAV与GU的距离，在UAV从每个传感器节点收集数据的同时，使所有传感器节点的最大能耗最小化；文献[11]研究了以UAV作为中继辅助用户与BS进行通信，通过优化UAV的飞行轨迹和发射功率，达到减少系统中断的目的。

与半双工HD(Half-Duplex)相比，全双工FD(Full-Duplex)是一种允许上行和下行链路传输同时进行的技术，能够将系统容量提升一倍。文献[12]提出了一种由FD-UAV充当中继的系统，该系统对中继的发射功率和轨迹进行联合优化，以达到最小化中断概率的目的；文献[13]针对蜂窝网络中基于设备到设备通信的FD-UAV中继系统的频谱共享规划问题，提出了一种连续凸算法，使总吞吐量在发射功率预算下达到最大。非正交多址接入NOMA(Non-Orthogonal Multiple Access)技术是5G无线通信的重要技术，不仅可以提高频谱利用率，还可以让更多的用户或设备接入网络[14 - 18]。与传统的正交多址不同，NOMA建立在多个用户同时共享一个资源块的思想上，例如系统把总频带划分成若干个子频带，又称子载波[14]，以此服务更多用户。用户在功率域进行多路复用，需要在接收端进行连续干扰消除解调。文献[19]提出了一种UAV辅助的NOMA网络模型，通过对UAV的轨迹和预编码向量进行优化，使UAV服务用户的数量最大化；文献[20]提出了一种NOMA的功率分配方案，通过调整UAV的高度使用户间的传输速率达到最大。上述文献只是将FD或NOMA技术单独应用于UAV通信的研究中，而将FD和NOMA技术同时应用于UAV通信中的研究则很少。文献[21]从速率的角度提出了一个FD-BS和多HD用户的通信系统模型，证明了FD-NOMA比HD-NOMA更优越，为本文研究奠定了理论基础。文献[22]针对无人机通信中频谱短缺的问题，提出了FD-NOMA和半双工正交多址接入HD-OMA(Half-Duplex Orthogonal Multiple Access)的方案，并给出了它们的闭式中断概率表达式，证明了利用FD-NOMA无人机通信提高频谱利用率的可行性。但是，上述文献并未对此类系统的容量性能进行分析。

本文构建了一个基于FD-NOMA的UAV通信系统模型，推导出了其精确遍历容量表达式和近似闭式表达式，分析了系统遍历容量和可达吞吐量的影响因子。具体工作如下所示：

(1)所提出的FD-NOMA模型允许具有不同用户服务质量和传输速率要求的用户同时进行传输和接收；

(2)通过对系统遍历容量进行分析，推导出了容量的精确表达式，解决了指数积分函数复杂的计算问题，得到了近似闭式表达式，分析结果表明，近似闭式表达式计算复杂度更低，误差更小。

最后的数值结果表明，增加UAV数量或NOMA功率都可以获得更好的容量性能；FD自干扰和信道噪声会对所提模型的性能产生影响。

2 系统模型

本文构建了一个由M个UAV和N个GU组成的基于FD-NOMA的UAV通信系统模型，如图1所示。UAV在距离地面高度为H的上空飞行，且UAV和GU之间的通信通过FD-NOMA方式完成。

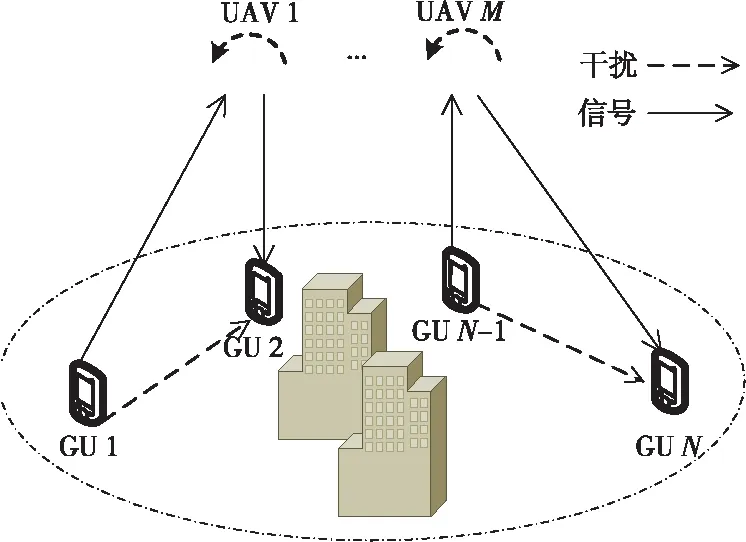
Figure 1 System model图1 系统模型图

本文部分符号说明如表1所示。

Table 1 Symbol description

为了清晰地表达，本文建立一个三维坐标系，如图2所示，将第i个UAV的位置表示为(xi,yi,H)，第j个GU的位置表示为(aj,bj,0)，第i个UAV和第j个GU的水平位置分别表示为si=(xi,yi)和kj=(aj,bj)。第i个UAV和第j个GU之间的信道增益如式(1)所示：

(1)

其中，Di,j表示第i个UAV到第j个GU的距离平方。

Figure 2 Three-dimensional coordinate 图2 三维坐标系

3 容量分析

3.1 城市场景

首先对城市场景中的系统容量Rc进行分析。在城市场景中，由于UAV和GU之间存在大量的反射线和折射线，所以采用瑞利衰落信道模型[23]进行分析。根据信道随时间变化的快慢，衰落信道分为快衰落信道和慢衰落信道。在接收端知道完整信道信息，而发射端只知道信息分布的前提下，信道容量通常被分为遍历容量和中断容量。一般在快衰落状态下考虑遍历容量，慢衰落状态下考虑中断容量。遍历容量是所有状态的瞬时容量平均值，而中断容量用于描述缓慢变化信道下的系统性能。UAV通信通常是时变信道，所以本文系统采用遍历容量。

基于香农定理,可以得到空中第i个UAV到第j个GU的容量表达式，如式(2)所示：

(2)

第i个UAV的容量可以表示为式(3)：

(3)

M个UAV的总容量可以表示为式(4)和式(5)：

(4)

即：

(5)

对信道噪声功率值进行归一化得到式(6)：

(6)

其中,λi,j,λi,l,λi,k表示归一化信道噪声功率值分配的FD传输的NOMA功率系数。

每个时隙的瞬时信干噪比SINR(Signal to Interference plus Noise Ratio)的概率分布函数如式(7)所示：

(7)

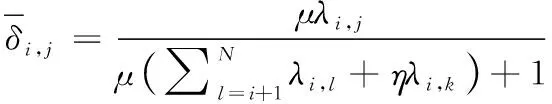
遍历容量推导过程如式(8)所示：

(8)

引入广义指数积分函数[24]，如式(9)所示：

(9)

将式(9)代入式(8)，基于FD-NOMA的UAV通信系统在城市场景中的精确遍历容量表达式如式(10)所示：

(10)

(11)

(12)

(13)

为了提高式(13)的精确度，本文还引入一个系数因子C，式(13)可进一步写为式(14)：

(14)

通过大量仿真实验可以发现：当C=1/4时，闭式表达式E2(x)与精确表达式E(x)的结果吻合度较好，且误差小于0.000 01。因此,可得到更准确的近似闭式表达如式(15)所示：

(15)

将式(15)代入式(10)可得到容量的近似闭式表达如式(16)所示：

(16)

3.2 郊区场景

在郊区场景中，存在视距路径LoS(Light of Sight)，接收信号服从莱斯分布[25]，将K作为莱斯因子，其计算如式(17)所示：

(17)

f2(δi,j)=

(18)

其中,I0(·)是第一类零阶修正贝塞尔函数。与城市场景中的推导过程类似，可以得到郊区场景的容量表达如式(19)所示：

(19)

(20)

在本文通信模型中，有M个UAV和N个GU，所以郊区场景下的精确遍历容量可以进一步写为式(21)：

(21)

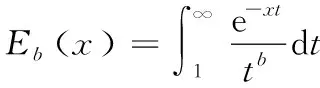
(22)

由式(22)可发现,误差主要来源于m的无穷级数，Eb(x)单调递减，则有式(23)：

(23)

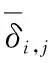
(24)

其中如式(25)所示的截断误差小于ε。

(25)

4 仿真及数值分析

本节通过仿真实验验证指数积分函数近似闭式表达式的有效性，同时比较了不同参数对系统容量的影响，以及设备数量和NOMA功率向量对系统容量的影响。

首先验证城市场景下指数积分函数E(x)、近似闭式表达式E1(x)和系数因子C=1/4时的近似闭式表达式E2(x)的结果，如图3所示。从图3的仿真结果可以看出，E(x)，E1(x)和E2(x)有着相似的曲率，E1(x)与E(x)之间存在较大的误差，而改进后的E2(x)与精确表达式E(x)之间的误差仅有0.000 01，说明了近似表达式E2(x)的正确性。其次，验证郊区场景下莱斯因子K对系统容量的影响，结果如图4所示。其他所有参数一致(1个UAV，3个GU，功率向量为ai=[1,2,3])，K做唯一变量，K越大，多径传播损耗越小，LoS分量越强，系统容量也随之增大，但其对系统容量的影响较小。

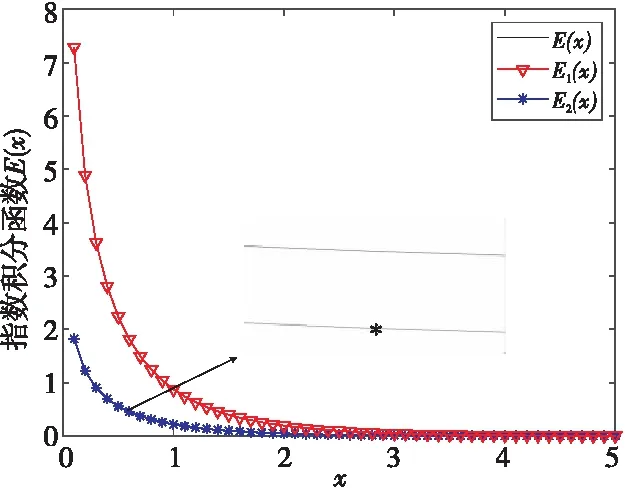
Figure 3 Comparison among E(x),E1(x) and E2(x)图3 E(x)，E1(x)和E2(x)的结果比较

Figure 4 Effect of K on capacity图4 K对容量的影响

在确保E2(x)的正确性和K的影响后，本文又进一步分别推导了2种场景下容量的近似闭式表达式，图5和图6分别验证了城市场景和郊区场景下UAV设备数量M和NOMA功率向量ai=[λi,1,…,λi,N]对系统容量的影响，比较了M=1，a1=[0.5,1,1.5]，以及M=2时，不同的NOMA功率向量(a1=[0.5,1,1.5]，a2=[1,2,3],a3=[2,4,6])对系统容量影响的仿真结果，其中2↔3,a1,a3，表示在FD-NOMA下，2个UAV设备传输信息给3个GU，它们的NOMA功率向量分别是a1和a3;1↔3,a1表示1个UAV设备传输信息给3个GU,NOMA功率向量是a1。由仿真结果可以看出，UAV数量对系统容量影响比较明显，随着无人机数量的增加，系统容量也会增加，增大NOMA功率向量也可以获得更大的容量，并且由于郊区场景中存在LoS路径，可以减少传播损耗，因此，郊区场景下的容量要高于城市场景下的容量。

Figure 5 Capacity comparison under different power vectors and UAV numbers in urban scenarios图5 城市场景下不同功率向量和UAV数量时的容量比较

Figure 6 Capacity comparison under different power vectors and UAV numbers in suburban scenarios图6 郊区场景下不同功率向量和UAV数量时的容量比较

最后，本文比较了两种场景下不同NOMA功率系数λi,k下系统可实现的吞吐量。为了验证仿真的有效性，只设置λi,k一个变量，其他参数设为定值。由图7和图8可以看出，NOMA功率系数越小，系统可达吞吐量越大，这是由于FD自干扰的增加，当λi,k=10时，SNR对系统吞吐量的影响微乎其微；在城市场景下，当λi,k=1，0 dB10 dB后，对系统吞吐量的影响很小；在郊区场景下，当λi,k=1，0 dB20 dB之后，对系统吞吐量的影响变小；当λi,k=0.1时，SNR成为影响系统吞吐量的主要因素。

Figure 7 Capacity comparison under different NOMA power coefficients in urban scenarios图7 城市场景下不同NOMA功率系数时的容量比较

Figure 8 Capacity comparison under different NOMA power coefficients in suburban scenarios图8 郊区场景下不同NOMA功率系数时的容量比较

5 结束语

本文提出了一种基于FD-NOMA的UAV通信系统模型，推导了城市和郊区两种场景下系统遍历容量的精确表达式，解决了式中指数积分函数的计算问题，并进一步推导出了具有任意小误差的近似闭式表达式。为了验证表达式的正确性，本文进行了一系列仿真实验，仿真结果表明，通过增加UAV设备或增大NOMA功率向量都可以获得更好的系统容量。最后,比较了NOMA功率系数和SNR对系统可达吞吐量的影响，即NOMA功率系数越小，系统可达吞吐量越大。未来的工作包括无人机布局优化，使无人机通信能力最大化。