分数阶微分Dλ型迭代学习算法在机器人控制中应用

周爱美，王 飞

（浙江广厦建设职业技术大学智能制造学院，浙江东阳 322100）

0 引言

工程生产过程中不可避免地会遇到各种类型的控制对象，其中有一类控制对象系统模型存在不确定性或是有些控制对象甚至无法精确建模，针对这种未建模动力学系统及模型不确定性动力学系统，可以使用一类数据驱动的控制方法，但是这类方法由于在初始阶段会出现较大的误差，从而系统收敛、镇定过程会比较长，控制系统的实时性达不到要求[1]；另外，有些算法精确性不高，满足不了工业生产的精度要求，以焊接机器人控制系统设计为例，其末端执行器的轨迹控制精度要求很高，需要实现精确跟踪[1-2]。迭代学习控制也是一类不需要精确建模的控制算法[3]，而且其产生的背景就是处理工业生产中的重复运行，因此，工业机器人的重复控制问题可以采用迭代学习控制加以解决：采用K时刻之前产生的输出误差对K时刻运行及K+时刻运行的控制输入量进行修正，而系统当前控制指令u(k)是在之前迭代步控制指令u(k- 1)的基础上，根据相应的偏差e(k- 1)做出调整得到[4]。

基于这一“在重复中学习”的思想，经过多次迭代，从而满足控制的精确跟踪要求。控制系统的另一项指标时效性要求则需要选择不同的迭代学习算法，整定出最优的参数。鉴于此，本文在传统迭代学习控制的基础上，提出了一种分数阶微分Dλ型迭代学习算法，这类算法可以很好地满足时效性和精确性要求，可以有效解决误差的微分量和积分量的计算分析，从而减轻测量噪声的影响。同时，在Dλ型迭代学习算法基础上，设计了一种自适应Dλ型迭代学习算法，增加迭代学习控制算法的应用场景。

1 迭代学习控制算法基础

迭代学习控制核心思想是基于误差来迭代修正输入。为了有效增加控制算法收敛速度、提升控制精确，作为输入量，除了误差值外，还包括获取误差的微分项和积分项，并通过参数整定的方式，获得最优的控制规律，以满足控制系统相对应的任务要求。总体而言，迭代学习控制只需要利用相对少的先验知识，通过不断的迭代循环计算，就可以完成精确跟踪[1]。

常见的迭代学习控制原理如图1 所示，其中迭代步数(0,Λj, ΛJ)为系统当前重复次数，每个重复周期∕迭代步数被分割成有限个采样点(1,Λk,ΛK)。迭代学习算法将前一个迭代步j-1的偏差送入学习函数L进行处理，和前一个迭代步j-1控制指令相加后生成当前迭代步j控制指令。即系统当前控制指令u(k)是在之前迭代步控制指令u(k- 1)的基础上，根据相应的偏差e(k- 1)做出调整得到：如果以前迭代步中的控制指令已经能达到相对较好的效果，那么当前控制指令只需在以前的基础上微调；如果以前迭代步中的控制效果不好，当前控制指令则需要做出相对较大的调整。

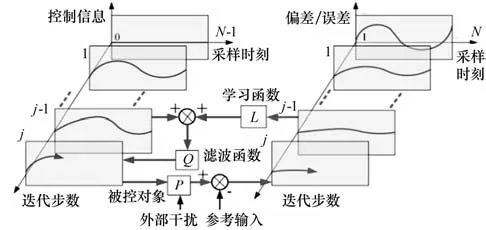
图1 迭代学习控制原理

学习函数L的选择具有较大的自由度，可以是线性或者非线性算子，学习函数L的形式决定了偏差信息以不同的方式反馈到控制指令中，因此，学习函数L的选取关系到迭代学习算法的收敛速度和控制精度等，因此，学习函数的选取以及参数的整定是算法设计的核心。

滤波器Q的设计需要综合考虑系统的稳定性、控制精确以及实时性要求[5]。如果将滤波函数Q选为1，表示历史信息百分百利用，即先前控制指令和对应偏差信息计算出来的当前控制指令被直接输入到被控对象P，这种滤波器Q的设计可以实现理论上的控制输出精确跟踪参考轨迹；而对于存在未知非周期性干扰的被控系统而言，由于历史信息包含随机误差，因此，会导致被控系统不稳定或出现振荡，这种情况下，可以将滤波函数Q设计成为低通滤波器，但是这样历史信息被没有被全部利用，控制系统在满足稳定性的前提下，控制精度和收敛速度将会受到一定的影响。

除了适应具有重复运动性质的被控对象外，迭代学习控制算法对于被控对象的数学模型的依赖性也比较低，鉴于此，迭代学习控制算法可以在工业机器人控制系统中被广泛应用。从而可以以较为简单的算法实现不确定性较高的非线性强耦合动态系统的控制，并高精度跟踪给定期望轨迹。

迭代学习的控制律用最简单的表述方式就是：

式中：uk(t)、uk+1(t)分别表示k、k+ 1时刻的控制信号；L为学习函数，常见的有PID型，PD型等。

D型迭代学习算法首先被构造出来，其形式为：

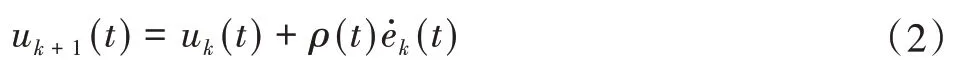
D型迭代学习算法，即微分型迭代学习算法，是指通过误差的导数e.

k(t)的迭代，但e.k(t)在实际应用中难以直接测量。为了解决这一问题，采用Dλ型迭代学习算法。

2 Dλ型迭代学习控制算法及流程

Dλ型迭代学习控制算法形式为：

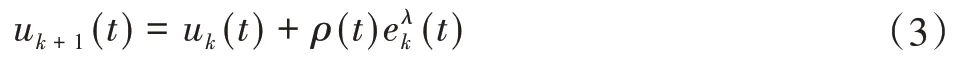
式中：为误差的分数阶导数。

分数阶微分系统与整数阶系统相比，有优点如下：（1）分数阶微分是整数阶微分的一种特例，这种算子除了具有整数阶微分的性质外，还具有一些其他的性质，比如，分数阶微分具有一定的记忆功能；（2）分数阶微分和整数阶微分相比，多了一个分数阶系数，因此，可以通过选取合适的系数得到更多的性能效果。

利用Grunwald-Letnikov 定义方法求解分数阶微积分的数值方法为：由于

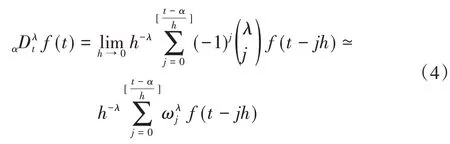
则有：

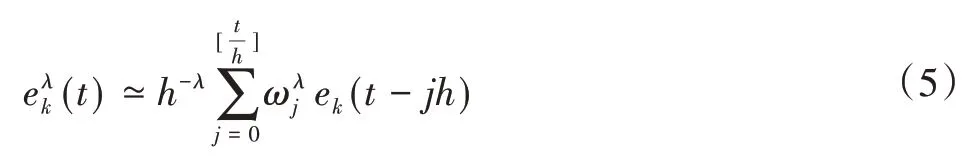
则式（4）可以写为：

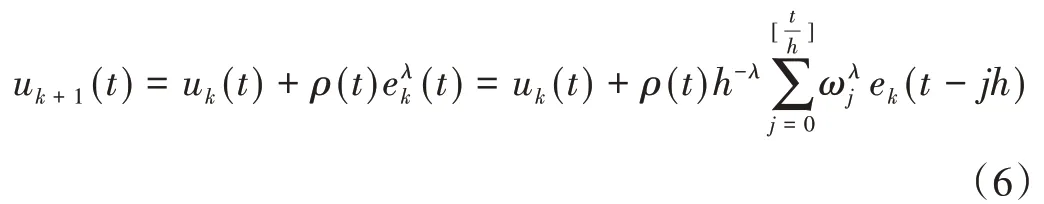
可由下面的递推公式得出，= 1，=(1-

Dλ学习控制结构如图2 所示，利用学习过程中保存下来的输出误差ek(t)及期望控制ud(t)，计算出分数阶Dλ控制器的增益矩阵。将此Dλ控制器加入到控制系统中，可以得设计出性能满足要求的控制系统。但是此类方法的鲁棒性较差，对于存在随机扰动较大的系统，这种方法存在局限性。

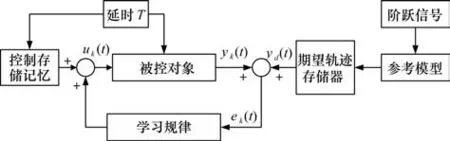
图2 Dλ学习控制结构

3 Dλ型迭代学习控制算法稳定性证明

定理1：对于线性离散系统，即

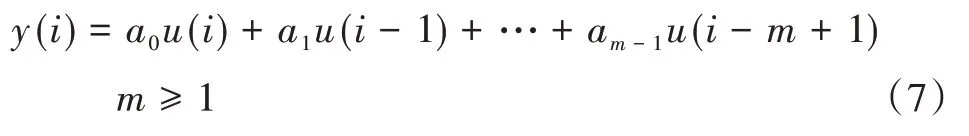
误差模型Ek=AΞk，采用迭代学习律Uk+1=Uk+BEλk，如果通过恰当设计学习矩阵B，使得如下矩阵不等式

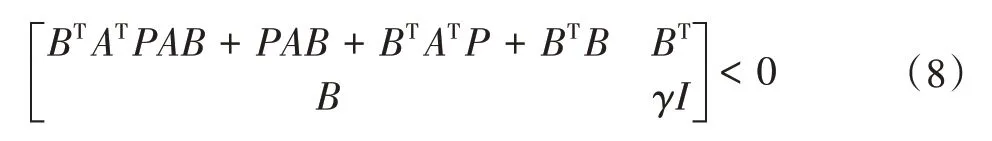
成立，其中γ为任意小的正数；P∈RN×N为正定对称常矩阵，那么系统误差Ek将收敛至零，控制输入Uk也将收敛至期望值Ud。

证明：定义Lypaunov函数，即

由此可知，通过恰当设计迭代学习矩阵B，使得矩阵不等式成立。那么Vk+1-Vk≤0，当Vk+1-Vk= 0定理1，证明完毕。

4 仿真分析

为了进一步验证本文方法的有效性，设计如下仿真模型。

有高阶差分形式的线性离散系统[3]：

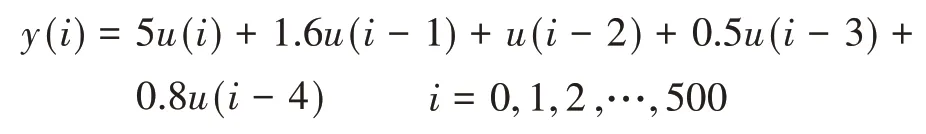
在实际控制中，考虑系统的不确定性，设系统参数的估计区间分别为：a0∈[2,8];a1∈[0,3];a2∈[0,3];a3∈[0,1];a0∈[0,1.6]。

系统期望轨迹设为：yd(i) = 2 + 0.5 sin(iπ∕500)

对比D型和Dλ型迭代学习控制算法，通过MATLAB仿真，仿真结果如图3～4所示。

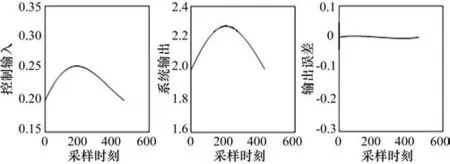
图3 普通D型迭代学习控制第5次迭代仿真效果

仿真分析时选取：

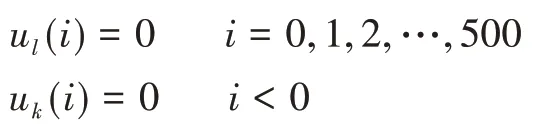
分数阶微分Dλ中λ参数通过参数整定的方法获得最佳值，进行本次仿真时，根据工程经验，选取λ= 1.25。这样可以得到相应的仿真结果。通过对比图3、图4可以看出，本文提出的分数阶迭代控制的精度要高出一个数量级，同时，Dλ迭代学习控制具有更好的收敛特性。

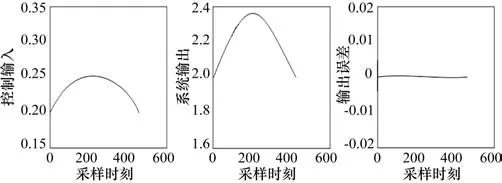
图4 Dλ迭代学习控制第5次迭代仿真效果

从仿真成果还可以看出在最后的几个采样周期，输出误差略为增大，这是由于可利用的误差项减少。为了解决这一问题，可以利用前面的误差项来进行多次迭代加以解决。

5 自适应Dλ型迭代学习控制算法

在Dλ型迭代学习控制算法的基础上，提出了一种Dλ迭代学习算法。理论与仿真结果均表明本文提出的Dλ迭代学习控制方法更加适用于工业机器人控制过程中，不仅不需要精确的机器人数学模型，而且相对于D型迭代学习控制算法控制效果更加精确，具有很好的收敛特性和稳定性。但是工业机器人运行环境比较复杂，当存在不确定干扰时，这种Dλ迭代学习控制算法不具有较强的鲁棒性，因此，需要将Dλ迭代学习控制算法和其他鲁棒性较强的算法相结合，比如自适应控制算法等，从而适应更多的工业机器人应用环境[6-7]。

5.1 自适应Dλ型迭代学习控制算法原理

自适应控制是一类鲁棒性很强的控制系统，因此，设计了一种基于自适应控制律的Dλ型迭代学习控制算法，原理框图如图5 所示，即在Dλ型迭代学习控制算法的基础上，引入一个自适应迭代项，通过这样的结合，自适应Dλ型迭代学习控制算法既可以完成机器人重复任务中的精确轨迹跟踪，又可以适应未知打扰动，从而增加控制系统的鲁棒性[8-10]。

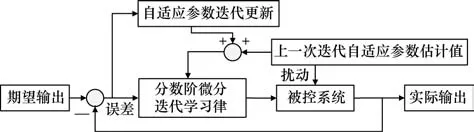
图5 一类自适应Dλ型迭代学习控制算法原理

根据原理框图，算法执行简单流程为：在有效时间范围[ ]

0,t，将k-1 步通过迭代计算得到的自适应参数估计值和第k步的系统误差ek(t)代入到自适应律，计算本次迭代的自适应参数估计值再将自适应参数估计值和系统误差ek(t)带入到控制律中，从而计算得出控制量uk(t)；控制量uk(t)作用于被控对象，得出实际输出，若输出满足性能指标要求，则迭代结束，反之，继续迭代学习直到达到性能指标要求为止[5]。

5.2 自适应Dλ型迭代学习控制算法应用举例

假设有机械人机械臂系统[5]，其数学模型可以使用朗格朗日形式表示为：

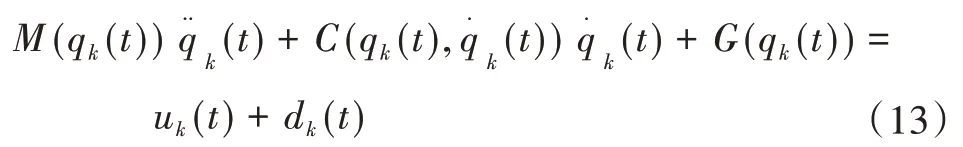
针对式（13）所示的机器人机器臂数学模型，设计自适应Dλ迭代学习控制律为[13]：

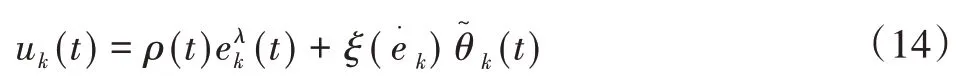
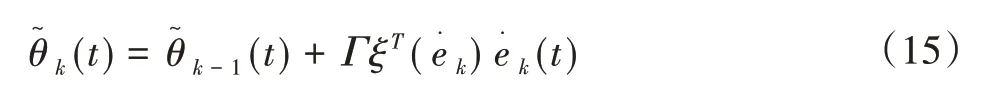
式中：ek(t)为角位移误差。

式（14）～（15）设计的控制律将自适应控制方法运用用到Dλ迭代学习控制系统中，这样其应用将更加广泛，特别是对于非线性不确定系统而言，可以很好地实现迭代学习控制和自适应控制都无法单独处理的控制任务。从实际工程应用的角度来看，迭代学习控制是依靠重复相同的控制任务来实现迭代轴上的精确跟踪，自适应控制用来保证时间轴上的渐近跟踪。这样，一个控制效果良好且稳定的控制器的设计会变得比较容易，因为在设计控制器时有两个可以努力的方向（时间域和迭代域）来稳定系统和调节控制效果[14-15]。

6 结束语

分析工业机器人的工作环境及工作方式，不难发现，工业机器人大都执行的是具有重复性质的任务，基于此，在选择控制算法时，迭代学习控制算法显得特别合适，这类控制算法既可以避免求取工业机器人的精确模型，又可以在重复任务中通过误差迭代的方式完成精确控制任务。

本文以工业机器人的控制系统设计作为研究对象，在D型迭代学习算法的基础上，将其扩展到分数阶微分领域，提出了一种Dλ迭代学习控制算法，进行了稳定性证明和仿真分析。仿真结果表明，Dλ迭代学习控制算法通过参数λ的整定可以实现跟踪误差更小，收敛速度更快。同时为了使Dλ迭代学习控制算法更加具有适用性，将Dλ迭代学习控制算法和自适应控制算法相结合，设计了一种自适应Dλ型迭代学习控制算法，此类方法兼具了二者的优势。但是从目前的工程实际情况来看，很难找到普遍适用的自适应律，想要更好地实现工业机器人的自适应性，还需要大量的控制理论研究和工程实现。