基于混合整数规划的P型玩具生产线平衡优化*

张萃珠，李志滔，余秋萍，赵 莹，何演铭，龙建宇，洪 颖

（东莞理工学院机械工程学院，广东东莞 523808）

0 引言

随着改革开放的不断深入，我国将继续加大制造业的发展，抓住全球经济一体化的机遇，不断从国外学习和引进先进的生产技术和生产体系，逐步完善和增强国内的制造业水平[1]。近些年来，随着电子信息技术的快速应用，在保证质量的同时，产品的生产成本随之升高，导致产品销售价格过高，以致国内市场订单量过少，所以企业想要提高国内订单量就必须降低生产成本。生产成本的降低离不开生产线效率的提高，生产线的平衡率、生产线节拍、瓶颈工序、生产线的生产布局等会影响生产线的效率[2]，因此，对生产线的平衡优化是解决生产线问题的重要任务。

为解决生产线问题，许多学者对生产线的优化改善做了不少研究，葛晓梅等[3]运用以生产线节拍为准则的启发式算法对家具装配线进行了平衡与优化，提高了装配线的平衡率。李柯[4]运用0-1整数规划的方法，根据生产现场状况建立数学模型，通过计算机编程求得最优解,对H 公司的生产线平衡率进行了优化，得到了最优作业分配方案。程丙警[5]对X公司Z型产品的生产线平衡问题进行优化，优化后的生产线各项指标都得到了一定的改善。王崇果[6]使用启发式算法对M 公司服务器产品生产线平衡问题进行改善优化，取得了比较明显的改善效果。李险峰[7]提出改进遗传算法，分析汽车装配生产线平衡问题，克服了传统遗传算法的应用约束。杨广强[8]在运用ILOG OPL的基础上对传输网资源使用能效进行优化分析，得到了优化的业务配置路由和规模。郭继东等[9]根据0-1 整数规划模型和Lingo 软件算出的工序排序，得到最优的生产节拍和平衡率，并重新规划了实木A 厂1号车间的布局。上述文献虽然都是对生产线进行平衡优化，但没有涉及到实际情况下的工序与工作站之间相互约束、半成品物流的约束等，因而在平衡优化生产线过程存在一定问题。

本文以W 公司的P 型电子教育智能玩具（简称P 型玩具）生产线为研究对象，从P 型玩具生产线实际情况及所遇到的问题出发，综合考虑半成品的相互传递、工序的优先关系、设备占用面积以及作业者的工作习惯等因素，结合大多数工序需依附在面壳上加工的特点，以及运筹学的相关优化理论知识和生产车间的生产状况，运用数学规划法对生产线的作业分配问题建立以最小化生产线节拍为目标的混合整数规划模型，通过ILOGOPL优化软件对模型进行编程求解，得到有效提高生产线平衡率和均衡分配作业的解决方案。

1 W公司P型玩具生产线现状分析

随着制造技术的不断升级更新，在保证质量的同时，产品的生产成本也随之升高。如何降低生产成本、获得更大利润和更多订单量是W 公司迫切需要解决的问题。该厂是典型的制造型企业，主要生产小批量多品种型的产品，同时存在着工艺路线不合理、作业分配不均衡、现场各种浪费等问题，导致人员和设备利用率低、人均产出不高，影响生产线效率的提高。该厂主要生产电子教育智能玩具等产品，本文选择了具有代表性的P型玩具作为研究对象，该产品的订单量是W 公司某一生产楼层客户订单量最大的订单之一，代表性高。通过秒表时间研究法对该产品各工序进行测时，得到每道工序的观测时间，再对每个工作者进行作业评定，取宽放率为10%，最后得到完成一件产品时每道工序的标准时间，其工序的相关数据如表1所示。

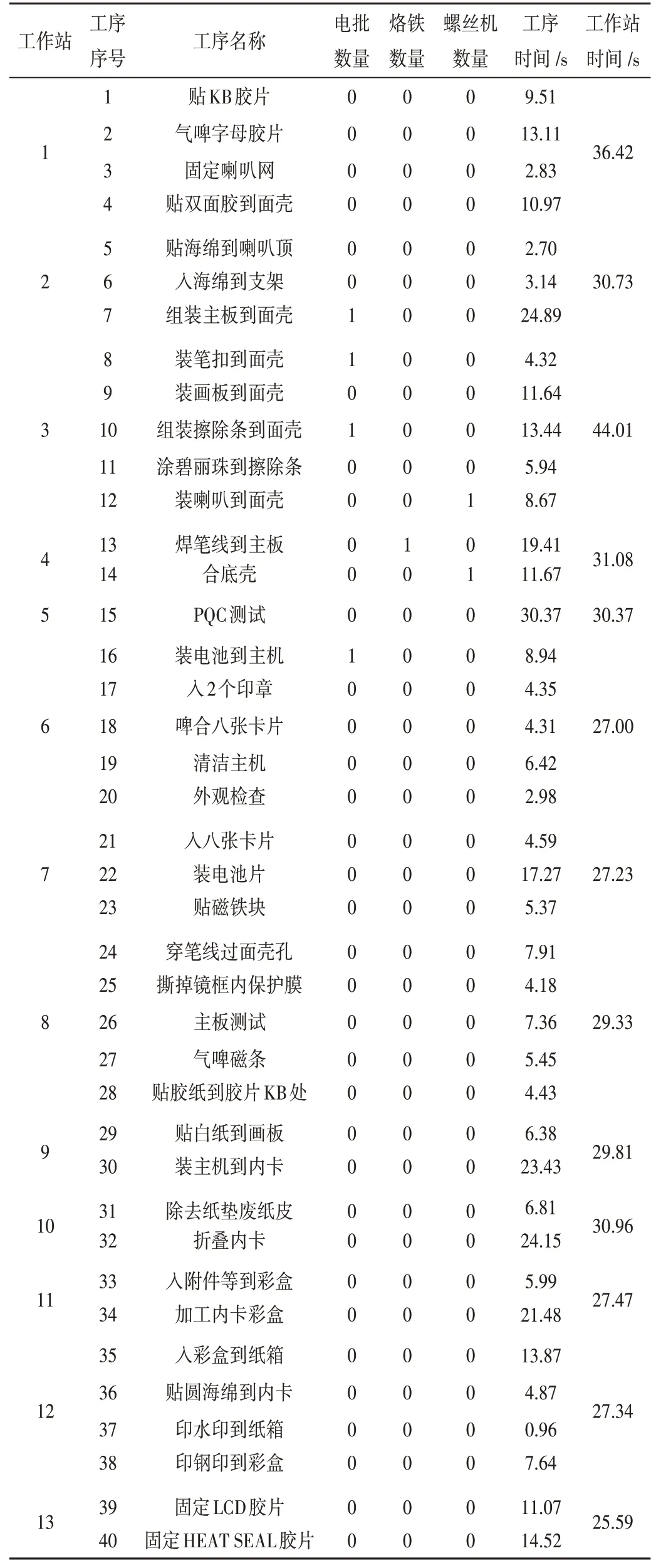
表1 工序的相关数据

P 型玩具工序繁多，作业复杂，所有作业由人工及部分小型半自动化设备共同完成。在整个生产工艺中，工序的加工和组装主要集中在面壳这个材料上，在其它材料上加工的不多。根据工艺结构及装配顺序，该玩具的工艺程序如图1所示。

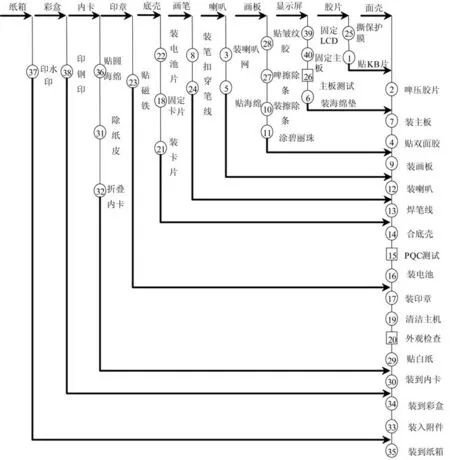
图1 工艺程序

本文主要研究P 型玩具生产线中的产品组装、测试到包装的工艺流程，根据P 型玩具的生产工艺和现场调研后绘制该产品优化前的生产线工位布局，如图2所示。从图中可以看出，该生产线布局呈现“E”字形，整条生产线采用手工传递的方式传递半成品。产品的组装、测试到包装都是在生产线上完成，工作站5为测试产品，工作站6主要为产品的外观检查，工作站9、10、11、12为产品的包装，其余的工作站为产品的组装。

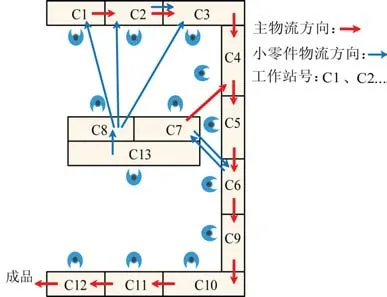
图2 优化前工位布局

通过表1得知，优化前P型玩具的作业内容分配到13个工作站，完成一件产品需要397.34 s。工作时间最长的工作站是工作站3，即是瓶颈工位，作业内容为“组装笔、画板、擦除条”，用时44.01 s，因此，生产线节拍为44.01 s。

生产线平衡率R以及生产线平滑系数SF的计算方法分别如式（1）和式（2）所示：

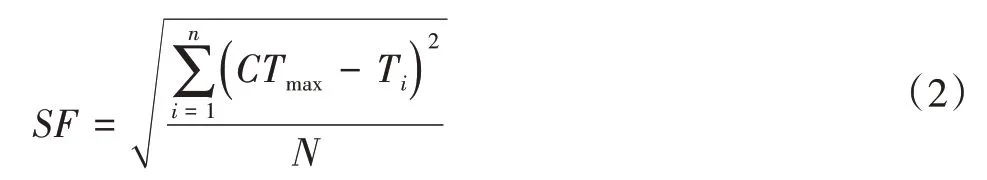
式中：Ti为第i个工作站时间；N为生产线工作站总个数；CTmax为工作时间最长的工作站时间。

根据现场收集的生产数据，计算优化前生产线平衡率Rb以及生产线平滑系数SFb：

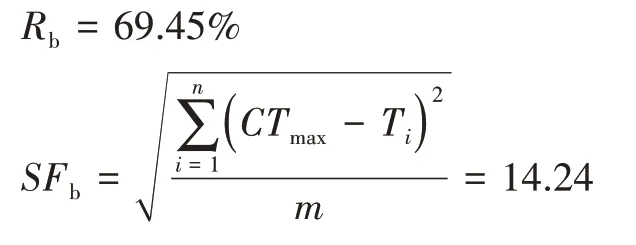
根据数据分析，可以发现问题：（1）P 型玩具的作业内容繁多，不同工作站之间的时间差距较大，生产线中的工序分配不均衡，造成部分人员忙闲不均；（2）有部分小零件物流需要进行无价值的跨工位传递的搬运动作，这种搬运方式需要工作者离开座位走动传递，不利于工作者持续作业；（3） P 型玩具生产线平衡率为69.45%属于低水平状态，生产流程不顺畅，作业内容分配不合理，影响生产效率提高。

2 P型玩具平衡优化数学规划模型建立

P 型玩具生产线属于单元化生产[10]，并且工位之间的半成品可以相互传递。因此，综合考虑半成品的相互传递、工序的优先关系、设备占用面积以及作业者的工作习惯等因素，结合大多数工序在面壳上加工的特点，建立混合整数规划模型的思路如下：以最小化生产线节拍为目标，先对工序进行基本约束，然后对不可独立加工的工序（即必须依附在面壳上加工的工序）进行优先关系约束，剩下可独立加工的工序（即不须依附在面壳上加工的工序）通过建立工序之间相互关系等方面的约束被安排到其紧后工序同一个或相邻的工作站上，最后再对所有工序进行工作地和设备等方面的约束，从而使得面壳的传递成为生产线主物流的方向。

2.1 问题描述

本文将建立针对P 型玩具的第二类生产线平衡问题的混合整数规划模型，即在工作站数量确定的情况下，将作业内容重新分配，使得生产线节拍最小。生产线占地面积、布局形状、所使用的设备等不变，在规划过程中需要考虑设备的占用面积、半成品传递的便捷性、使用工具的冲突性等因素。在这种单元化的生产线中[11]，半成品可以在相邻工位传递，但尽量取消跨工位传递。

2.2 参数定义

模型建立过程中相关参数的定义：Ti为第i道工序的标准作业时间；N为工序的数量；J为工作站的数量；SMi为第i道工序需用到自动螺丝机的数量；SDi为第i道工序需用到电批的数量；SIi为第i道工序需用到烙铁的数量；M为一个很大的数；Precedences为工序的优先关系集合，Precedences=(a，b)表示工序a不能安排在工序b所在工作站的后面来完成；Locations为某工序必须安排在某工作站的集合，Locations=(a，b)表示工序a必须安排在工作站b；Togethers为两道工序必须在同一个工作站的集合，Togethers=(a，b)表示工序a和工序b必须在同一个工作站；Nearbys为两道工序必须在同一个或者相邻工作站的集合，Nearbys=(a，b)表示工序a和工序b在同一个或者相邻工作站；Nearbysindexs为Nearbys中的两道工序与工作站的集合，Nearbysindexs=(a，b，j)表示工序a、b是否分配在工作站j内或相邻的工作站的集合。

2.3 建立混合整数规划模型

混合整数规划模型（Mixed Integer Programming，MIP）是指在线性规划问题中要求决策变量有部分必须取整数值，另一部分可以不取整数值的整数最优化数学模型，具有3 个要素：决策变量、约束条件、目标函数[10]。

2.3.1 定义决策变量

CTmax为非负实数，表示生产线节拍，xij为0-1 变量则有：

yabj为0-1变量(a,b,j∈Nearbysindexs)，则有：

2.3.2 定义目标函数MinimizeCTmax

目标函数使得生产线的节拍最小化，即该生产线瓶颈工位的标准作业时间尽可能小，最终使得生产线平衡率最大。

2.3.3 约束条件

（1）工序基本分配约束

每个工作站所有工序的标准时间的累加不能大于生产线节拍：

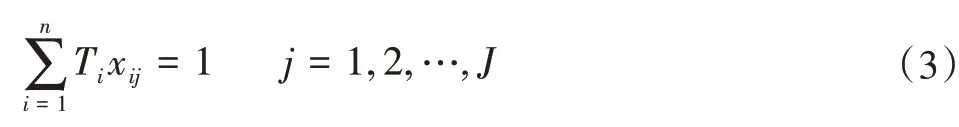
每道工序必须且只能被分配到一个工作站：

每个工作站必须分配有工序：

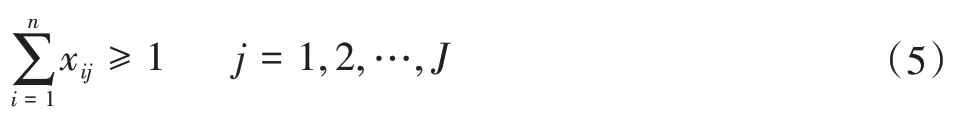
（2）不可独立加工工序约束

工序优先关系的约束。即如果工序a被分配到工作站j，那么工序a的紧前工序不能被安排到工作站j后面的工作站，工序a的紧后工序不能被安排到工作站j前面的工作站，约束如下：

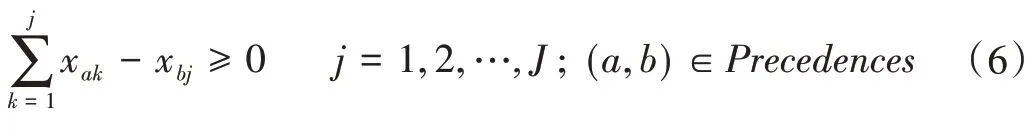
（3）可独立加工工序约束

某些工序必须在同一个工作站中。考虑到某些特殊的工序需要特殊处理，例如，像“印水印”等包装工段需要走动作业，不固定在某些位置，这类工序安排在同一个工作站能减少其他人员的走动，提高整体作业环境。

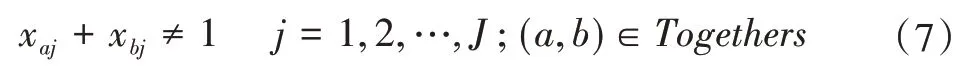
某两个工序必须在同一个或相邻的工作站。这些是组装一些小零件的工序，并且不需要依附在面壳上也能作业。例如，“贴海绵到喇叭”这道工序不需要依附在喇叭上也能作业，它的紧后工序是“装喇叭到面壳”，那么，它可以与紧后工序在同一个工作站，也可以在紧后工序前面或后面的工作站。

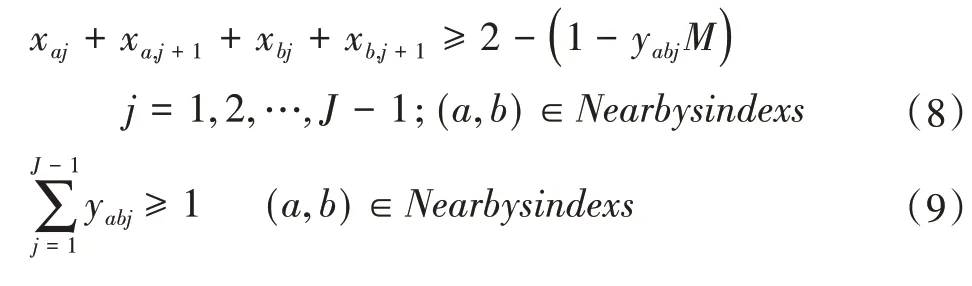
（4）其他约束

工作位置的约束。由于某些工序加工设备大小的限制，需要被安排到特定的位置，才不会对半成品的传递等方面产生不利的影响。

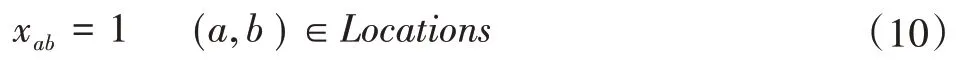
设备数量的约束。在这种布局下主要考虑自动螺丝机的影响，因为自动螺丝机的体积较大，通常一个工作站内容不下两台，因此，同一工作站内自动螺丝机的数量不能超过1台。其约束如下：

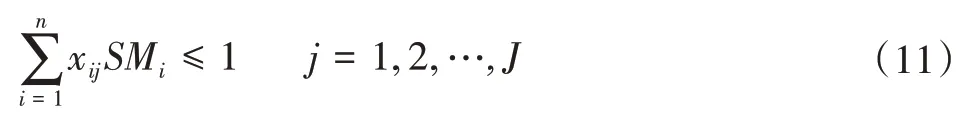
工具操作限制。经过动作分析，电批与烙铁不能再同一个工作站，电批与烙铁都是使用右手操作，而将这两个工具一起放在右侧，容易造成绕线的麻烦甚至被烫伤的危险。其约束如下：

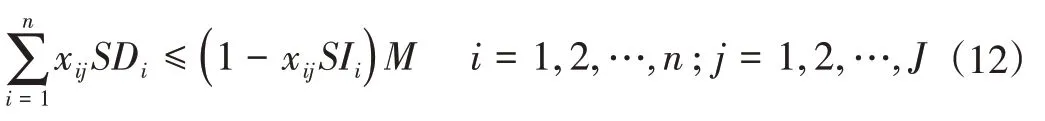
3 实验结果分析

使用ILOG OPL 软件求解以上数学模型，得到优化后的工序分配表，如表2所示。

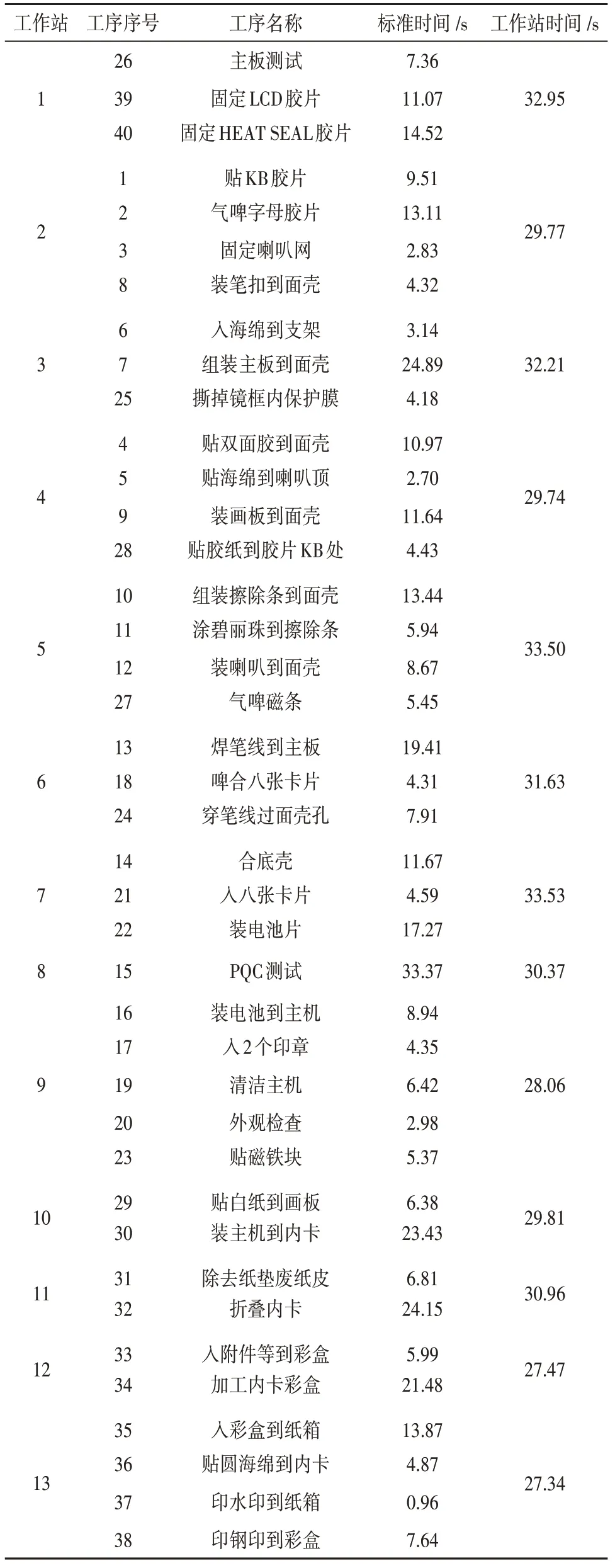
表2 优化后工序分配表

根据式（1）和式（2）计算出优化后的生产线平衡率Ra以及生产线平滑系数SFa分别为91.16%和14.24。

根据以上各项指标，列出优化前后生产线评价指标进行对比，如表3 所示。根据优化前后工作站的时间分布绘制优化前后生产线平衡对比图，如图3所示。

表3 优化前后生产线评价指标对比

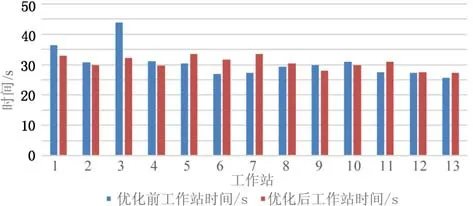
图3 优化前后生产线平衡对比

优化后的生产线工位布局如图4 所示，布局形状不变，仍然呈“E”字形，但需要跨工位传递半成品的小零件物流由原来5个减少为1个，这个物流是把组装完成的PCB 板从工作站1 传递到工作站3，此过程每次传递10个PCB板，重量轻，对与整体的工作影响不大。

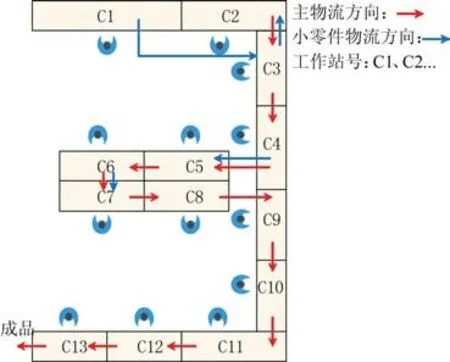
图4 优化后工位布局

综合以上分析，通过混合整数规划优化后，生产线的节拍由原来44.01 s减少为33.53 s，减少23.81%，生产线平衡率由原来的69.45%提高到91.16%，属于持续高水平状态，生产系统稳定；生产平滑系数由原来14.24减少为3.61，减少74.63%，同时结合图3 分析可知，优化后，生产线每个工作站的标准作业时间较为均衡，不存在工作站的标准作业时间过高或过低的现象。在所有工作站中，作业时间最短的工作站与瓶颈工作站之间的时间差值低于7 s，因此，生产线内不会出现明显忙闲不均的现象。由图4 可知，优化后的工位布局在物流上更加的顺畅，减少了生产线内人员不必要的流动。

4 结束语

本文通过分析生产线的现状和收集生产现场的相关数据，结合其结构特点，指出工序分配不均衡、跨工位传递、生产线平衡率低是导致生产线效率低的主要原因。本文应用数学规划法构建了以最小化生产线节拍为目标的混合整数规划模型来对生产线进行平衡优化，并运用ILOG OPL 软件对模型进行编程求解。结果表明，P 型玩具生产线节拍减少23.81%，平衡率由69.45%提高至91.16%，生产线平滑系数减少74.63%。与优化前相比，优化后的生产线内物流更加顺畅，作业分配更加科学合理，工作站之间的作业负荷也更加均衡，实现了生产线平衡率的提高和作业的均衡分配，提高了生产效率。