基于DeepLabV3与GAN的雷达时频混叠多信号智能检测与分离

韩文草 孙闽红 王之腾 仇兆炀

（1.杭州电子科技大学通信工程学院，浙江杭州 310018；2.陆军工程大学通信工程学院，江苏南京 210001）

1 引言

雷达侦察面临的电磁环境日益复杂，信号样式日趋多样，信号密度不断增高，接收信号数量呈指数级增长。常规的雷达信号处理方法［1-5］逐渐无法适应复杂电磁环境下的雷达信号侦察需求，而随着人工智能及大数据技术的深入发展，雷达侦察正朝智能化方向快速发展。

在雷达信号智能检测方面，现有的研究成果主要有：朱新挺等人［6］使用卷积神经网络实现电磁信号的智能检测；李启飞等人［7］使用基于AlexNet深度卷积神经网络实现低信噪比下水下目标电磁异常信号的检测；李杰等人［8］使用掩码-区域卷积神经网络（Mask R-CNN）实现了对线性调频信号（LFM）重叠情况下的检测。然而，上述方法存在着一些不足，如：无法对信号进行分离、只能检测时频不重叠信号、可检测的信号样式单一等。

在多信号分离方面，Miao Feng 等人［9］使用小波包和快速独立分量分析实现了多源信号分离。文献［10］提出了利用深度聚类的方法来提高信号分离的性能。然而，上述方法也存在着诸如需要足够的先验信息、无法对单通道信号进行分离等不足。

针对上述不足，本文提出一种基于DeepLabV3网络［11-14］与生成对抗网络（Generative Adversarial Networks，GAN）的时频混叠多信号的智能检测与分离方法。首先，DeepLabV3 网络能够很好的对图像进行像素级实例分割［15］，是目前语义分割［16］领域中非常主流的分割算法之一。V3 中加入的ASPP是一种能够获取多尺度上下文的架构，能够让任意的特征图都有确定大小的特征向量来表示。该网络能够对时频图中不同类型的信号区域进行精准分割，同时也能够对信号重叠部分进行有效区分。其次，针对信号分离，考虑到GAN 具备用生成器和对抗器的对抗训练来自动调整信号参数的优点，提出用GAN 提取信号的有效信息，对分离后存在缺失时频信息的各信号分量实现精确还原。借助Deep⁃LabV3 与GAN 网络模型，本方法可以实现对时频混叠多信号的智能检测与分离，且具有可处理信号样式多样、同时到达信号个数不限等优点。

2 多信号智能侦察算法

本算法对雷达信号的智能侦察主要分为信号检测、分离与重构三个部分，其中信号检测与分离由DeepLabV3 实现，信号的重构功能由GAN 实现。首先对接收到的时频混叠信号进行时频变换得到时频数据与时频图，将时频图输入DeepLabV3 网络获取各个信号分量的时频位置与标签信息，组合成为各个信号在时频图的掩膜区域（Mask）。将图像的掩膜区域映射到时频数据中，对掩膜区域以外的信号时频分量进行滤波即可实现信号主体与无关分量的分离。对于信号的时频重叠区域，同样进行掩膜滤波滤除重叠部份，并对滤波后的时频数据进行时频反变换得到时域残缺波形，将残缺波形输入GAN 网络进行重构即可得到完整信号。算法步骤如表1所示。

表1 算法步骤Tab.1 Algorithm steps

算法流程框图如图1所示。

2.1 数学模型

设存在K个时频混叠的未知雷达信号s1(t)，s2(t)，…，sK(t)，且信号的接收时间区间为T，频率范围为F，则接收信号x(t)可以表示为

式中，sall(t)=表示K个雷达信号的叠加信号，n(t)表示高斯噪声。另外，式中K个信号的时宽、频宽可各不相同。

记TF[·]为时频变换函数，则对x(t)做时频变换得到X(t，f)，其可以表示为

通过DeepLabV3对X(t，f)进行定位掩膜滤波的过程可以等效为时频滤波器H(t，f)，它能够将信号所在时频区域之外的噪声去除，可表示为

则输出结果Y(t，f)为

式中，N′(t，f)为Sk(t，f)非零时频位置上噪声，且N′(t，f) ≪N(t，f)。对Y(t，f)进行时频反变换可以得到

当信噪比（SNR）较大时，n′(t)对信号的影响十分小，式子可以简化为

重叠信号存在残缺部分，需要使用GAN 对残缺的信号进行还原。将GAN 网络视作一个时频滤波GAN(t，f)，则

2.2 信号检测

DeepLab 网络是由Chen 等人与google 团队［17］于2014年提出的，该模型是为了应对语义分割而专门设计的。

DeepLabV3 编码部分采用ResNet-50/101 来提取特征，在第4个残差块中采用了膨胀卷积方法，并且把批量归一化加入空洞空间金字塔池化（Atrous Spatial Pyramid Pooling，ASPP）模块进行优化，模型结构如图2 所示。对比于之前的DeepLab 系列模型，V3 进一步改善了空洞卷积，使网络在级联模块和空间金字塔池化的框架下，能够获取更大的感受野从而获取更多尺度的信息。

将信号的时频图输入DeepLabV3 网络进行训练，能够将时频图中信号所在的时频位置与背景噪声进行像素级别的分割。如图2 中的Prediction 所示，图中噪声对应这黑色区域标签，不同的高亮区域为信号时频分量所在位置，图中最亮的区域为信号的重叠时频区域。

2.3 信号分离

对信号进行检测之后，将时频图中信号有用的位置信息映射到时频数据中，对信号的有用分量进行定位并进行掩膜滤波，剔除无关的噪声分量。当多个信号在时频图上存在重叠时，将重叠部分的时频数据作为其他标签同噪声一起被滤除，仅留下信号非重叠的部分，得到不同标签对应的多个非重叠时频数据分量Sk(t，f)，分别对Sk(t，f)进行反时频变换得到sK(t)，完成信号的分离。

2.4 信号重构

类比于图像重构技术，信号重构是指将一段不完整的信号使用一定的手段复原。GAN 在图像重构的应用有着十分成熟的应用，在信号重构领域却鲜有应用。Goodfellow等［16］提出对抗生成模型GAN框架，生成网络模型通过学习数据的分布将低维的随机分布样本映射生成高维空间样本，鉴别器网络模型学习区别真实样本和生成样本，建立最大和最小机制联合训练生成和鉴别网络。模型的对抗损失函数为

式中，s是输入概率分布为p(s)的真实信号，E[·]为期望函数；z是残缺信号，D(s)为判别器，判断信号是否真实的概率，G(z)为生成器重构的信号，使用V(G，D)来衡量G和D的相似度。生成对抗网络模型结构如图4所示。

本文对于信号重构的思路为：在模型训练时，首先将时频重叠区域缺失的信号数据输入到生成器G中，其次是将完整信号和生成器输出的信号输入判别器模型中进行误差判别，若不满足要求则继续代入生成器中再次进行重构直至达到与完整信号足够相似。通过训练好的GAN 模型自动对信号残缺部分的估计重构，能够在有效保留信号非重叠部分的同时重构出与原信号误差较小的信号。

3 实验与结果分析

3.1 实验环境及参数设置

本文实验配置参数设置如表2所示。

表2 实验配置参数设置Tab.2 Experimental configuration parameter settings

网络参数设置如表3所示。

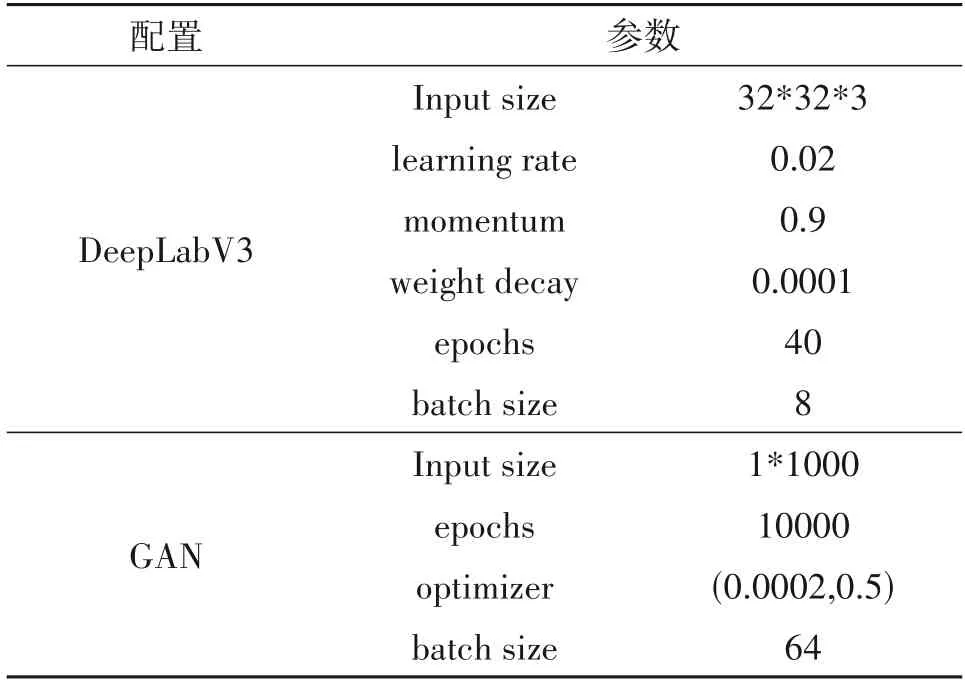
表3 实验网络参数设置Tab.3 Network parameter settings

3.2 获取数据集

仿真产生时频域存在重叠的3 种雷达信号分量，分别为单频脉冲（MP）、线性调频（LFM）脉冲以及非线性调频（NLFM）脉冲，本文中NLFM选用二次函数调频信号，其频率表示为

式中，f0为信号的初始频率，k1、k2是调频参数。对三种信号的参数设置为如表4 所示。信噪比范围设为-15 dB～15 dB，步长为3 dB。每个SNR 下产生参数随机的三类训练样本数各1000个，测试样本数各为200个。

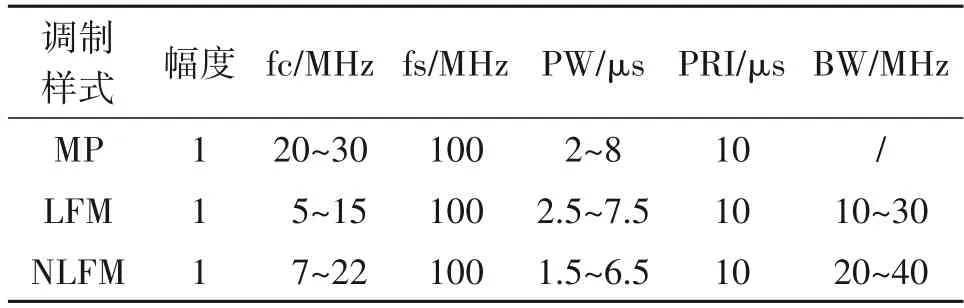
表4 信号参数设置表Tab.4 Signal parameter settings

对分段后的混叠信号进行短时傅里叶（Short Time Fourier Transform，STFT）变换，为均衡时频分析后的时间分辨率和频率分辨率，窗函数选用长度为128 的海明窗。在信噪比为6 dB 时，给出某个混叠信号的波形和时频图如图5所示。

从图5（c）时频图可以看出，三个信号在时、频域均同时存在重叠。图5（a）、（b）中的时域波形和频域波形混叠严重，无法辨别信号个数与调制类型。

3.3 仿真实验

3.3.1 信号检测

在3.1 与3.2 节的实验设置下对不同SNR 下的信号进行检测。将时频图训练集和训练标签输入表3 中的DeepLabV3 网络进行训练，在本实验环境下每次训练耗时15 至20 分钟内得到检测模型。给出SNR为15 dB时的检测结果如图6所示。

由图6 结果可以看出，本文方法不仅可以有效的检测出信号的数量以及调制类型，还能够有效检测出信号的重叠区域。分别在不同信噪比下，对DeepLabV3 模型进行训练和测试，使用GC（Global Correct）［18］和mIoU（mean IoU）［19］这2 个指标来对训练模型进行评估。GC的定义为

式中，C，R表示时频图的行（Row）数与列（Column）数。pc，r表示模型对第i行第j列的像素类别判断结果为

式中，K表示每个样本中的脉冲信号标签类数，在本实验中K取3。AreaOverlap，k为第k个样本的真实区域面积，AreaUnion，k为第k个样本预测区域与真实区域面积之和。IoUk表示第k个信号的IoU值。

实验结果如图7 所示。可以看出，在SNR 为−3 dB 时，该网络的GC 已经达到了95%以上，mIoU达到了85%以上。

信号检测中常采用检测率（TPR）作为算法性能的评价指标［20］，TPR的定义为

式中，N为所有正样本数，NP为预测的正样本数。

为验证网络对信号的检测能力，指定SNR 范围为［−6 dB，9 dB］，步长为3 dB，每个SNR 下采取1000 次蒙特卡洛实验。对MP、LFM 和NLFM 信号随机重叠的信号进行检测。同时，考虑到文献［8］方法无法对非线性调频信号进行检测，对其选取同批次MP、LFM 重叠信号进行方法有效性对比，得到结果如图8所示。

由图8 可以看出，当SNR 为−3 dB 时，本方法对信号的TPR 能够达到95%以上。且当SNR 小于0 dB时，本文方法的检测率显著提高。

3.3.2 信号分离

从图6（b）可以看出，即使信号存在不同程度的时频重叠，网络也能成功的识别分类，并且能够检测出信号的重叠部分。对重叠部分定为其他类别标签，将混合信号时频图的标签信息映射到时频数据进行掩膜分离，并对分离后的时频数据进行反时频变换得到单个信号。得到结果如图9、图10所示。

3.3.3 信号重构

从图9、图10 的结果可以看出，仅仅用掩膜方法对重叠的多信号进行分离，会不可避免的损失重叠部分的信息，还需要用GAN 对损失部分进行信号修复。实验环境和参数如表4 所示，将残缺信号输入生成网络并于完整信号在判别网络中进行对比，在本实验环境下每次训练耗时30 至40 分钟内得到检测模型。以图10 中所示的NLFM 信号为例对其进行分离复原，并且分别将原始信号、残缺信号与修复信号进行脉冲压缩，得到的结果分别如图11、图12所示。

在图11 中，（c）是对（b）中残缺信号的时域波形进行修复后的结果，对残缺信号的时、频域均实现较好的重构效果。从图12 中三种信号的匹配滤波结果可以看出，重构信号与原始信号的脉压输出非常相似，表明本文方法在对信号估计的同时保留了原信号的相位信息，不影响后续的脉压处理。

在不同信噪比下对分离后重构的信号与原始信号进行差异分析，其中信号相似度使用相关距离ρXY进行衡量。给出ρXY的定义为

实验结果如图13所示。

从图13 结果可以看出，当信噪比大于5 dB 时，修复信号与原始信号的相关系数高于0.8，差异较小。结合图11、图12 和图13 结果，以及与文献［8］中仅仅对信号的时频图像进行像素值修复的方法进行对比，本文着眼于重叠信号在信号层面的修复，在工程中更具有实际意义。

4 结论

本文将深度学习引入到雷达信号的检测、分离与重构中，研究多个信号在时频域混叠时，如何通过网络来智能准确地对不同信号进行检测、分离与重构。对比文献［8］方法，解决了调制类型和数量的受限的问题，可实现对非线性调频信号的检测，在SNR 为−3 dB 时，mIoU 能够达到85%，在SNR 为6 dB 时，分离后的信号与原信号相关系数高于0.85。且本文从保留雷达信号特性的角度出发，提出的算法保留了雷达信号的特性，便于后续的雷达信号处理工作。值得指出的是，本文方法需要依靠大量的数据集对网络进行训练，如何对数据进行轻量化处理来减少训练成本是下一步需要研究的问题。