馈能悬架的多模式智能控制策略
代 萍,温 欣,李以农,b
(重庆大学 a. 汽车工程学院;b. 机械传动国家重点实验室,重庆 400044)
电动汽车的发展对汽车悬架系统提出了新的挑战。主动悬架采用作动器代替传统的弹簧和阻尼器,能改善大多数工况下车辆的操纵稳定性和乘坐舒适性,但存在的能耗过大等问题使其在电动汽车中未得到广泛应用[1-2]。因此,主动悬架的馈能成为悬架的研究热点[3-6]。文献[7]中针对基于直流(DC)电机执行器的主动悬架设计了主动和能量回收控制器,该控制器能够以2种模式运行:主动控制模式(提高乘坐舒适性)和能量回收模式(回收能量)。馈能悬架的控制是进行馈能研究的基础,对悬架进行控制的算法和策略不同,所达到的控制效果也有差异,其中最优控制由于其完善的理论基础被广泛应用。最优控制方法中的线性二次型高斯(linear quadratic Gaussian, LQG)控制算法适用性强,能够通过给出最优性能指标来确定状态变量和控制变量的加权矩阵,LQG控制的关键是选择合适的性能指标加权系数。文献[7]和文献[8]通过反复调试来确定加权系数,操作简便,能达到一定的控制效果,但是费时、低效且适应性差。文献[9]和文献[10]利用层次分析法(analytic hierarchy process, AHP)来确定主动悬架性能指标的加权系数,时间成本低、适应性好,但计算过程中存在一定的主观片面性。而粒子群优化(particle swarm optimization, PSO)算法对性能指标进行求解具有速度快、收敛性好以及结构简单等优点,因此选择基于粒子群优化的LQG控制方法对馈能悬架进行主动控制,为后续馈能控制的研究奠定基础。对悬架馈能的研究,从控制策略方面来看,文献[11-15]通过不同控制策略,提高了悬架的动力学性能和能量回收能力,但是这些文献都没有考虑模式切换问题,单一模式的控制策略不能适应悬架复杂多变的工作环境。文献[16-18]设计了多模式控制策略,通过模式切换控制策略达到了提高动力学性能和能量回收能力的目的,但局限是没有考虑动力学性能以及能量回收能力会因车辆行驶状态不同而发生变化的情况。为解决这个问题,笔者在多模式切换控制策略中引入舒适性因素。
笔者采用永磁(PM)直线电机作为主动悬架系统的执行机构,基于最优控制理论设计了主动悬架LQG控制器,采用层次分析法(AHP)和粒子群优化(PSO)方法确定性能指标的权重系数,在此基础上,提出了一种新的考虑驾驶员舒适性因素的多模式切换控制策略,从而实现不同模式下的策略切换,实现主动悬架的能量回收。
1 建立馈能悬架系统模型
1.1 7自由度整车动力学模型的建立
建立车辆悬架系统动力学模型是主动悬架系统设计、性能分析与馈能特性研究的基础。为此,采用如图1所示的7自由度整车动力学悬架模型[19],整车模型参数如表1所示。
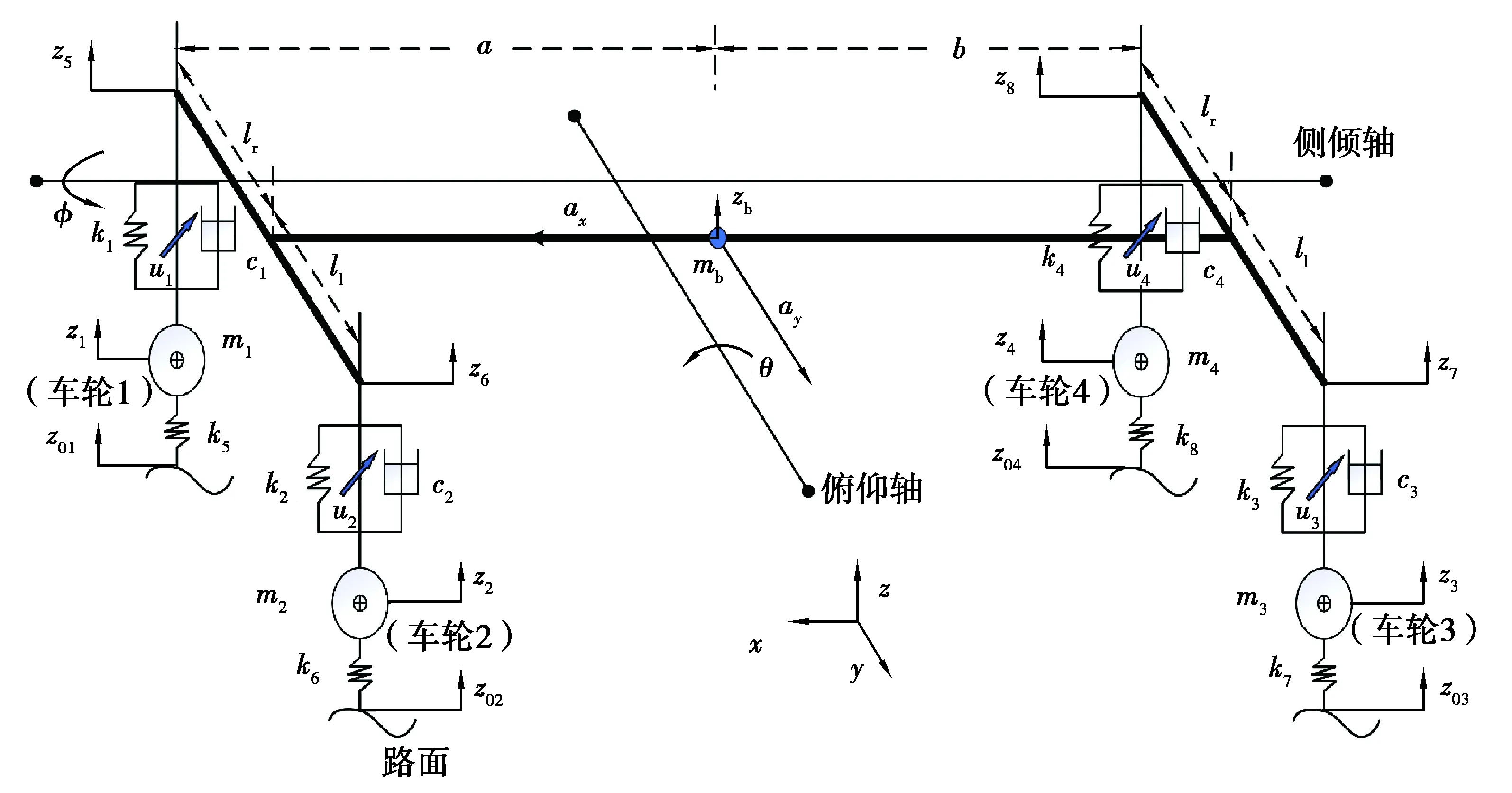
图1 7自由度整车动力学模型Fig.1 7-DoF full vehicle dynamic model
动力学模型的微分方程如下:
(1)


表1 整车模型参数
当俯仰角θ和侧倾角φ都非常小时,悬架在车身位置处的垂直位移方程为:
z5=zb-llφ-aθ,z6=zb+llφ-aθ,
z7=zb+llφ+bθ,z8=zb-llφ+bθ。
(2)
在评价馈能主动悬架的性能时,主要考虑乘坐舒适性和安全性,即考虑车身垂直加速度、车身的俯仰与侧倾、悬架动挠度以及轮胎动行程等性能指标。选取车身质心垂直位移、侧倾角、俯仰角、侧倾角速度、俯仰角速度、轮胎垂直位移、轮胎垂直速度以及路面垂直位移作为状态变量X,选取车身质心垂直加速度、侧倾角加速度、俯仰角加速度、悬架动挠度以及轮胎动行程作为输出变量Y:
(3)
馈能悬架系统的状态空间方程为

Y=CX+DU,
(4)
式中:W是高斯白噪声的输入矩阵,W= [w1w2w3w4]T;U是主动悬架的输入矩阵,U= [u1u2u3u4]T;A为系统状态矩阵;B为控制输入矩阵;C为输出矩阵;D为传递矩阵;G为干扰矩阵。
1.2 路面输入模型
选择滤波白噪声作为随机路面输入,则路面不平度对4个车轮的激励为
(5)
式中:z0i表示路面垂直位移;f0=0.1 Hz表示下截止频率;G0表示路面不平度系数;v0表示车速;wk(k=1,2)是前轮对应的白噪声,wn(n=3,4)是后轮对应的白噪声,wn相对于wk受到一定的延迟,延迟时间可定义为τ=(a+b)/v0。选择路面不平度系数G0=6.4×10-5m3的B级路面,车速v0=20 m/s的工况,通过Matlab/Simulink软件仿真,得到路面位移曲线如图2所示。
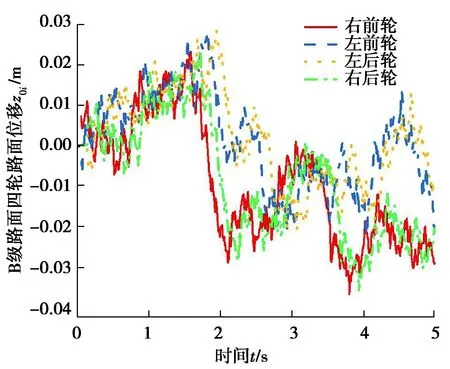
图2 随机路面位移曲线Fig.2 Random road displacement curve
1.3 馈能悬架LQG控制器设计
PM直线电机悬架的主动馈能控制器是基于最优控制原理,其控制框图如图3所示。它有2种工作模式:基于舒适性的主动控制模式与基于馈能的能量回收模式。能量回收控制是以主动控制器为基础的。因此,首先讨论悬架主动控制器的设计。

图3 馈能悬架控制框图Fig.3 Energy regenerative suspension control block diagram
对馈能悬架进行LQG最优控制,主要考虑两个方面。一方面是保证车辆的平顺性和操纵稳定性,即尽可能地降低车身垂直加速度、俯仰角加速度、侧倾角加速度、悬架动挠度以及轮胎动行程;另一方面,要减少能量的消耗,即减小作动器的控制力,确保设计的控制量最小。考虑各项性能评价指标,建立指标泛函如下:
(6)
式中:qr(r=1,2,3,4,5,6)分别表示车身垂直加速度、侧倾角加速度、俯仰角加速度、悬架动挠度、轮胎动行程和控制力的加权系数;Q是输出变量的权重矩阵;R是控制输入的权重矩阵。公式(6)可以改写为二次型函数的形式:
(7)

(8)
因此,馈能悬架系统的状态方程为

(9)
由公式(8)可知,要获得控制效果良好的反馈增益矩阵K值,需要选取合理的性能评价指标权重系数。这里基于粒子群优化对LQG控制器的权重系数进行选取,具体流程如图4所示,其中变量是权重系数q1,q2,q3,q4,q5和q6。

图4 基于粒子群优化的LQG控制器优化流程图Fig. 4 Flow chart for optimizing LQG controller based on PSO
为解决性能评价指标之间的数量级差异问题,建立粒子群优化适应度函数L:
(10)
基于粒子群优化方法进行计算,得到各性能评价指标的权重系数为q1=9.881 5,q2=9.885,q3=9.898 6,q4=9.882 5,q5=3.26×105和q6= 2×10-5。因此,最佳控制增益矩阵KPSO为:
KPSO=104×

KAHP=103×


表2 悬架性能均方根值对比
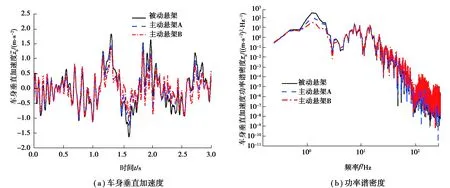
图5 车身垂直加速度及功率谱密度Fig. 5 Vehicle body acceleration and its power spectral density
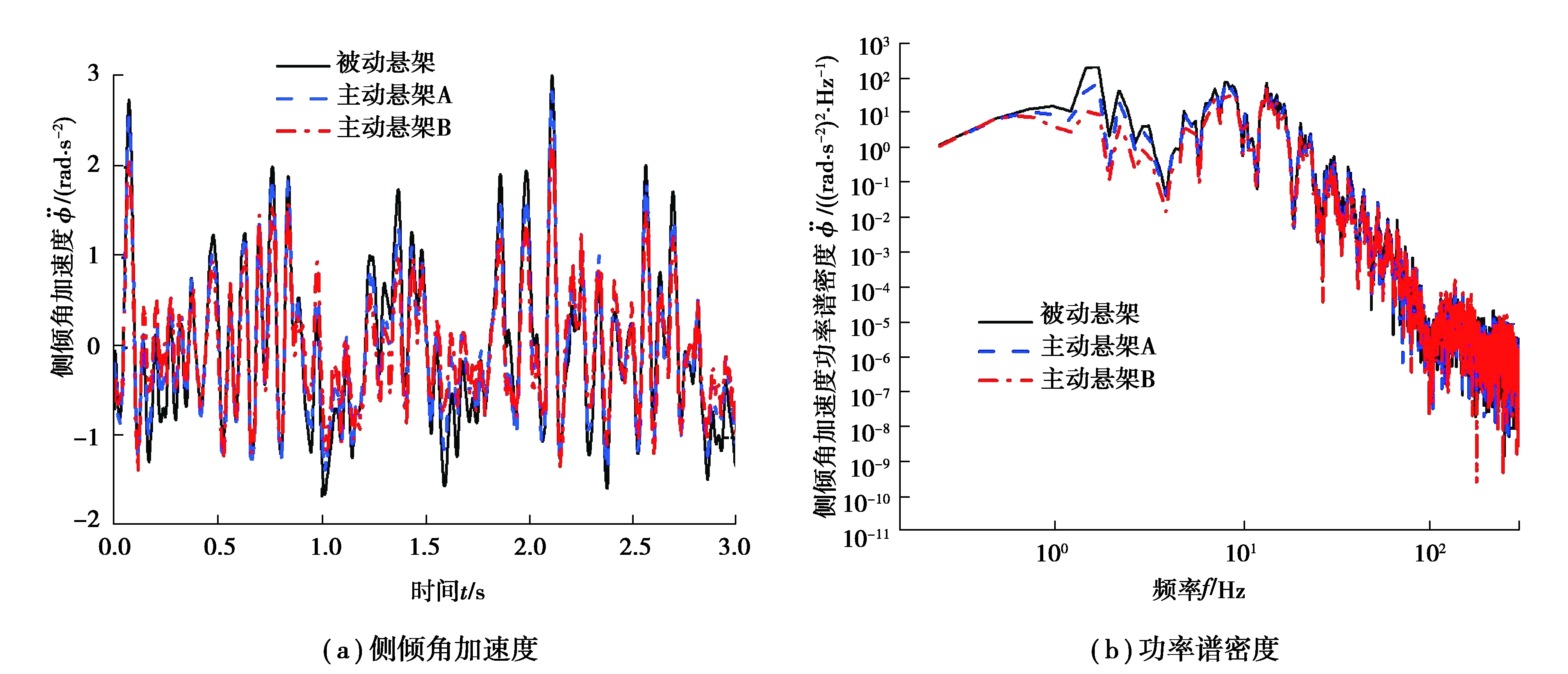
图6 侧倾角加速度及功率谱密度Fig. 6 Rolling angular acceleration and its power spectral density
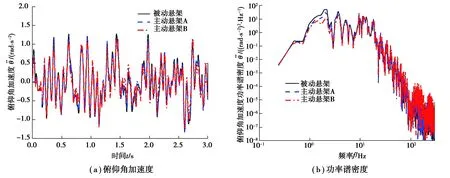
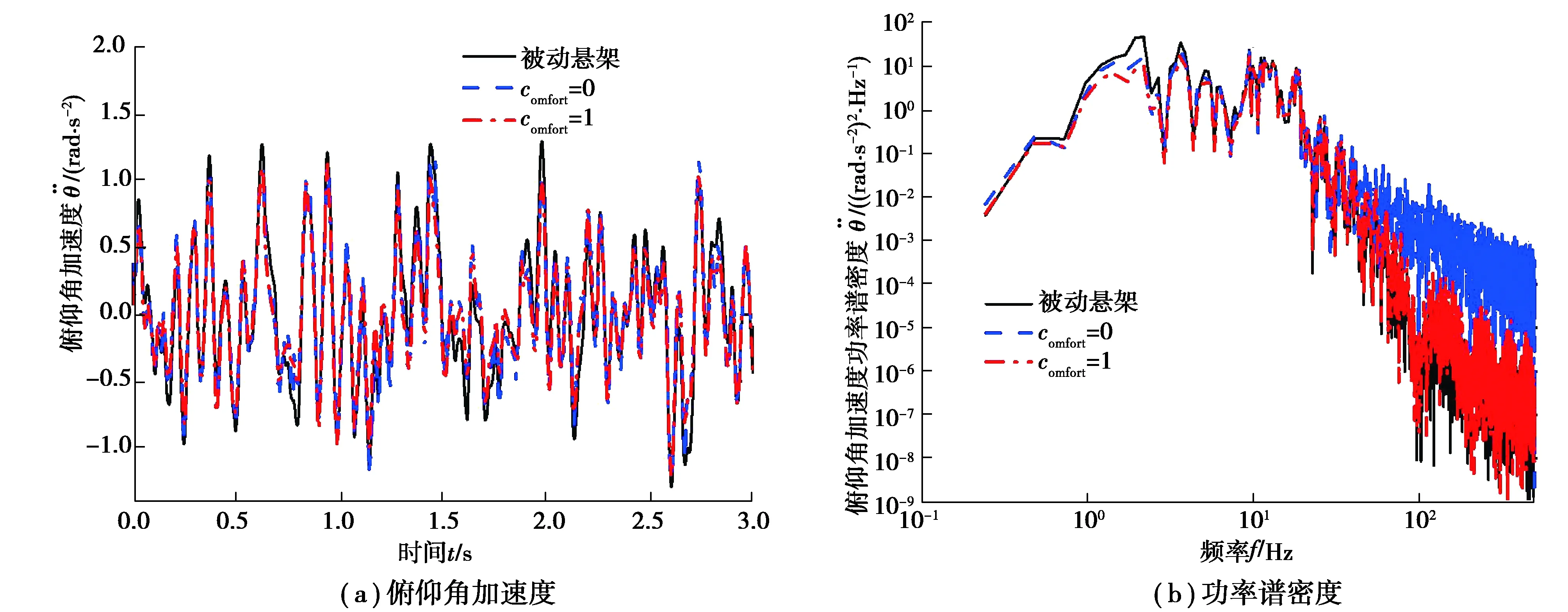
图7 俯仰角加速度及功率谱密度Fig. 7 Pitching angular acceleration and its power spectral density
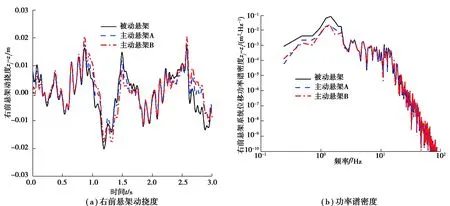
图8 右前悬架动挠度及功率谱密度Fig. 8 Right front suspension dynamic deflection and its Power spectral density
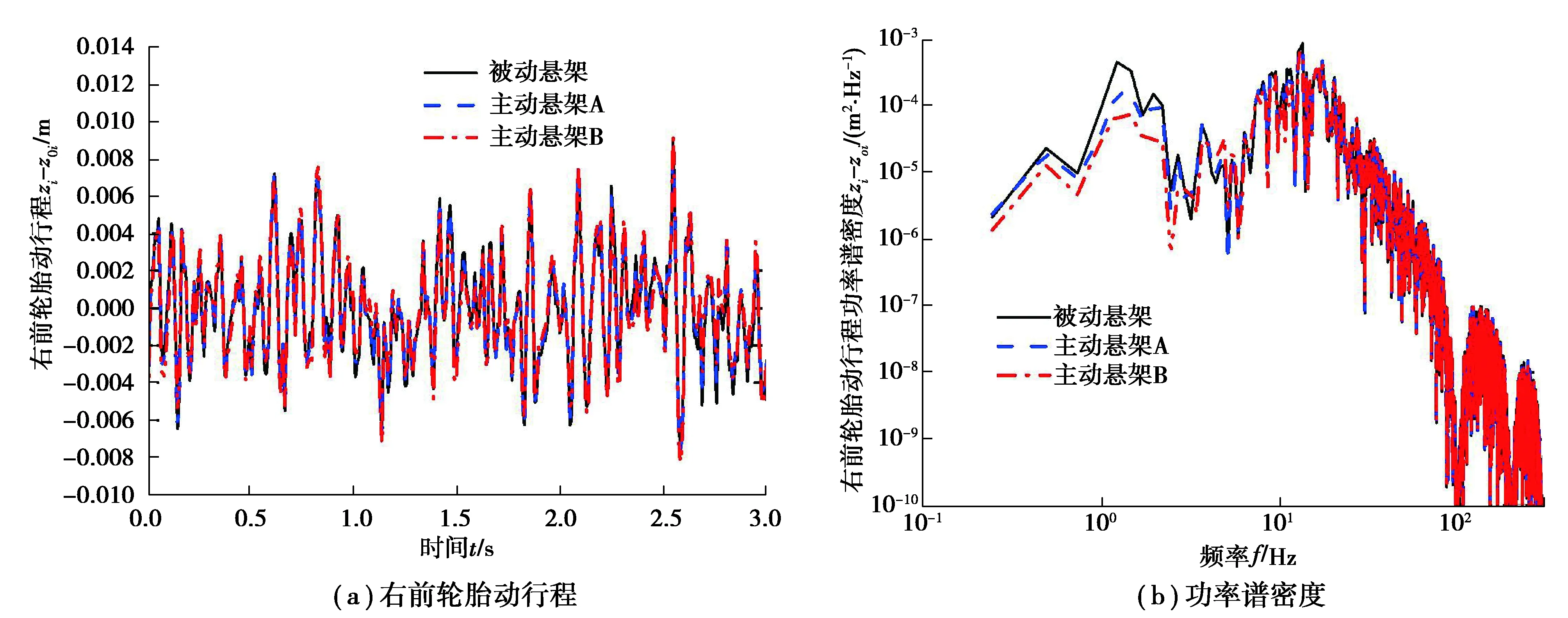
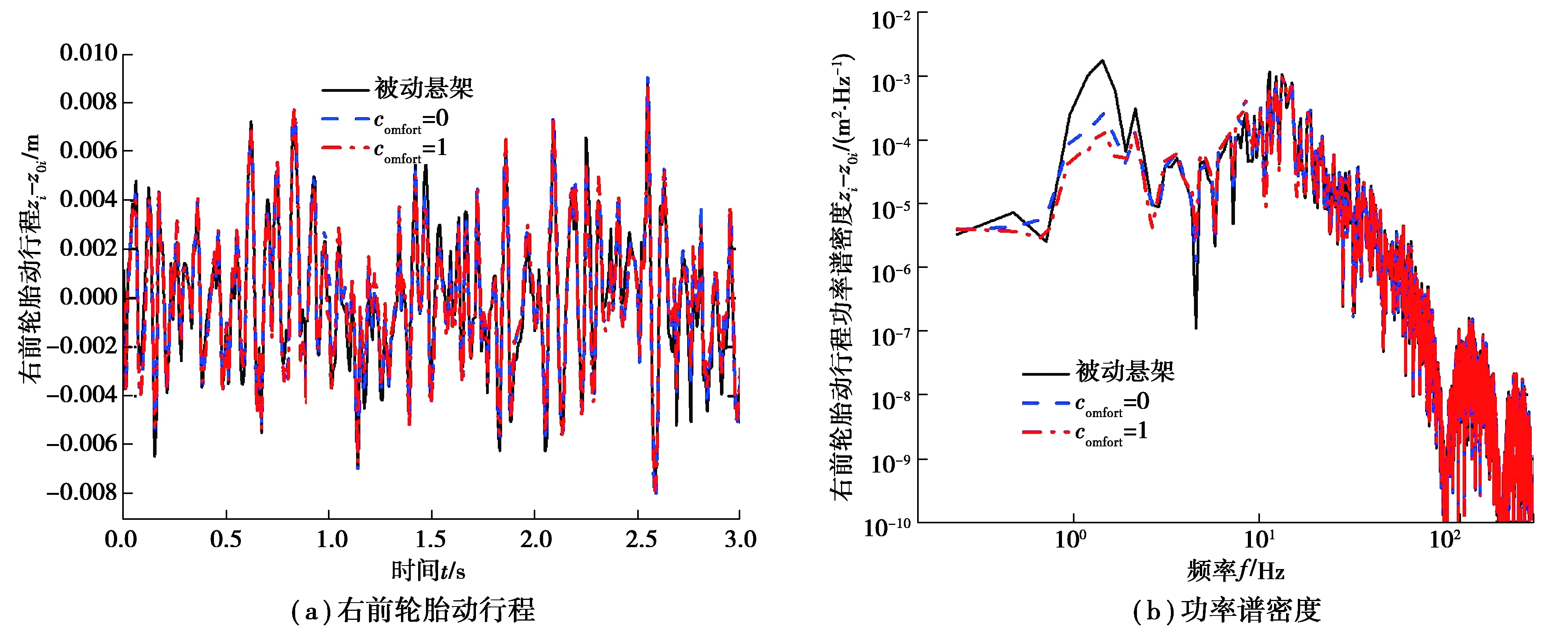
图9 右前轮胎动行程及功率谱密度Fig. 9 Right front tire dynamic displacement and its power spectral density
从图5~9中的(a)图以及表2可以看出,与被动悬架相比,主动悬架A、B的车身垂直加速度和侧倾角加速度均方根值显著降低,其轮胎动行程控制效果也得到改善;主动悬架B的俯仰角加速度均方根值明显减小,但主动悬架A减小得不明显;主动悬架A、B的悬架动挠度均方根值大大降低(表2),峰值有所增加但在合理范围内(图8)。与主动悬架A相比,主动悬架B可以显著改善乘坐舒适性。从图5~9中的(b)图可以看出,与被动悬架和主动悬架A相比,主动悬架B在与车辆乘坐舒适性有关的频段中隔振效果良好;与汽车操纵稳定性相关的轮胎频率幅值在低频下略有减小。因此,本文中所设计的基于粒子群优化的LQG控制器是有效的。
2 馈能悬架多模式切换控制策略
在PM直线电机驱动的主动悬架中,PM直线电机的工作状态可以分为2种:电动机状态和半主动电磁发电状态,如图10~11所示。其中U是电路的电源电压,R和Re是电枢的电阻,E是感应电压,i是电枢电流,忽略电枢电感。在电动机状态下,电源电压和感应电压的方向相反,电枢电流与感应电压的方向相反,但是电磁力的输出与电机的运动方向相同,即电磁力有助于PM直线电机的运动。此时电能转换为机械能,消耗了电源的能量。在半主动电磁发电状态下,电源电压和感应电压的方向相反,电枢电流与感应电压的方向相同,但是电磁力的输出与电机的运动方向相反,阻碍了电机的运动。此时可以通过改变电阻Re来控制电磁阻尼力,即把PM直线电机当作半主动作动器。在发电机状态下,电动机将机械能转换为电能,为电源充电。

图10 电动机状态 Fig.10 Electromotor state
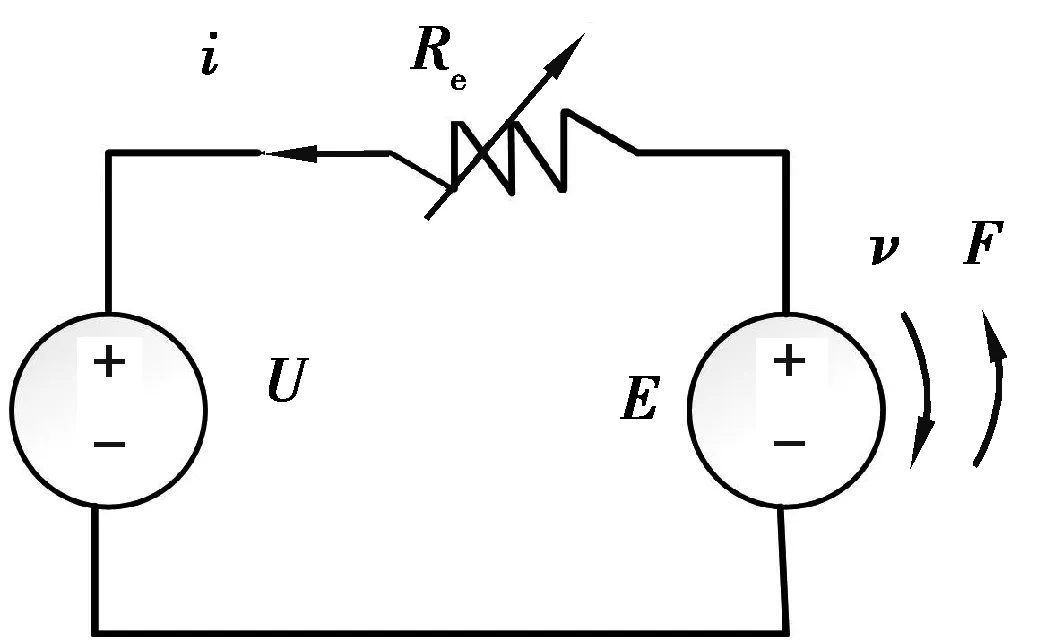
图11 半主动电磁发电机状态Fig.11 Semi-active electromagnetic generator state
一般情况下,当车辆能量较低时,需要牺牲乘坐舒适性来补充能量;当车辆能量充足且乘客状况不佳时,以提高乘坐舒适性为主。因此,引入舒适性因素设计了一种新型智多模式切换策略,以提升不同工况下的车辆动力学性能和馈能效果,其切换逻辑如图12所示。
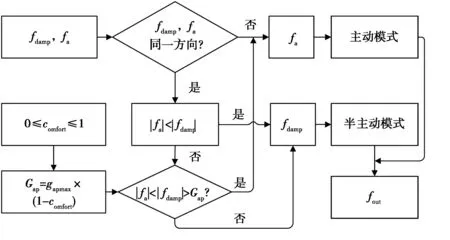
图12 智能控制策略原理Fig.12 The principle of intelligent control strategy
图12中,fdamp为阻尼力;fa为期望作动力;comfort为舒适性因素,comfort=0表示最大馈能状态,comfort=1表示最大舒适性状态;gapmax为限位开关值;Gap为切换差值。本文的智能控制策略最终分为4种状态和2种模式:
1)当fdamp和fa反向时,悬架工作在主动模式,以保证悬架的动力学性能。
2)当fdamp与fa同向且|fa|<|fdamp|时,悬架工作在馈能半主动模式跟踪作用力,以确保更好减振效果的同时回收振动能量。
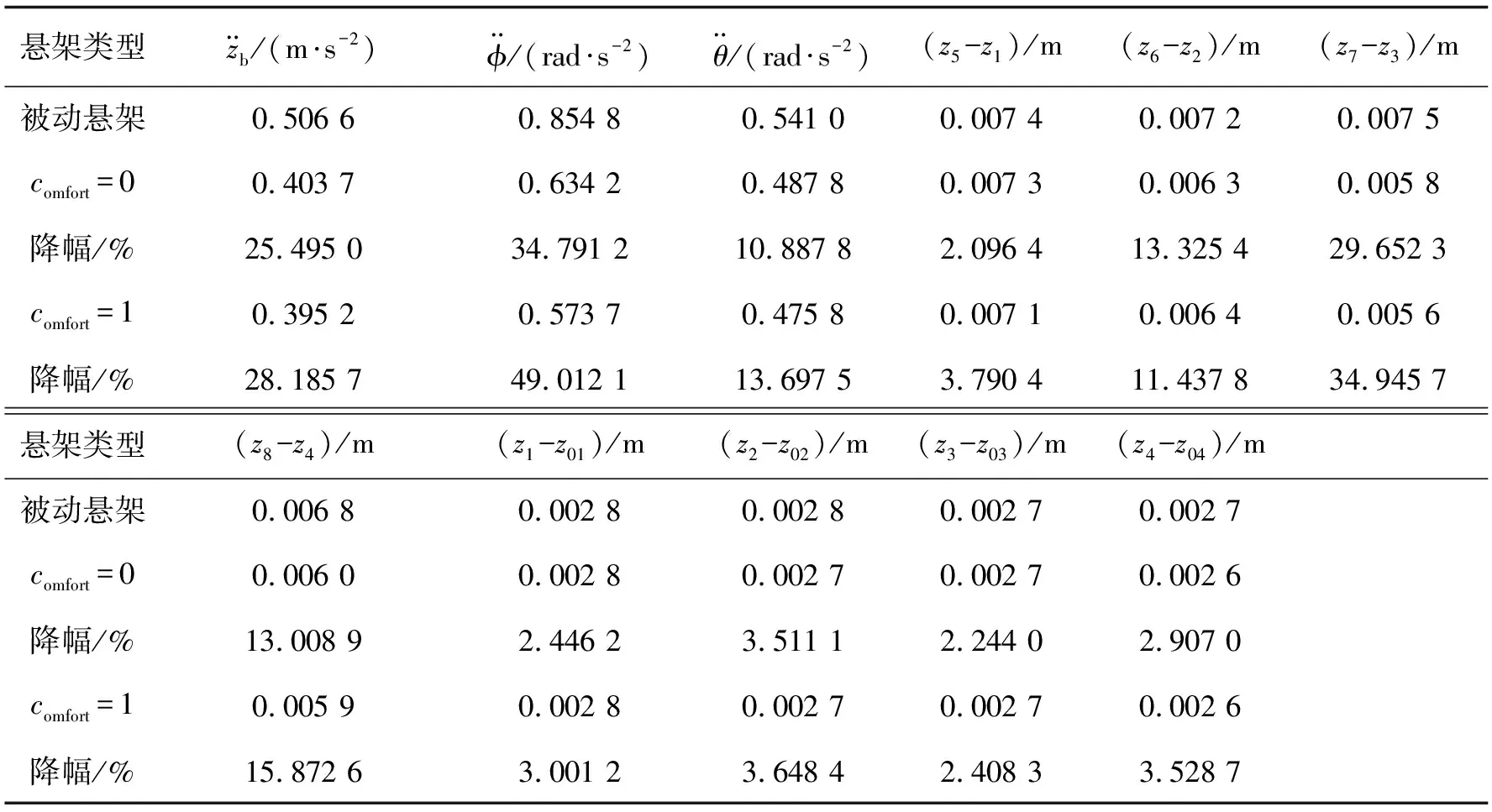
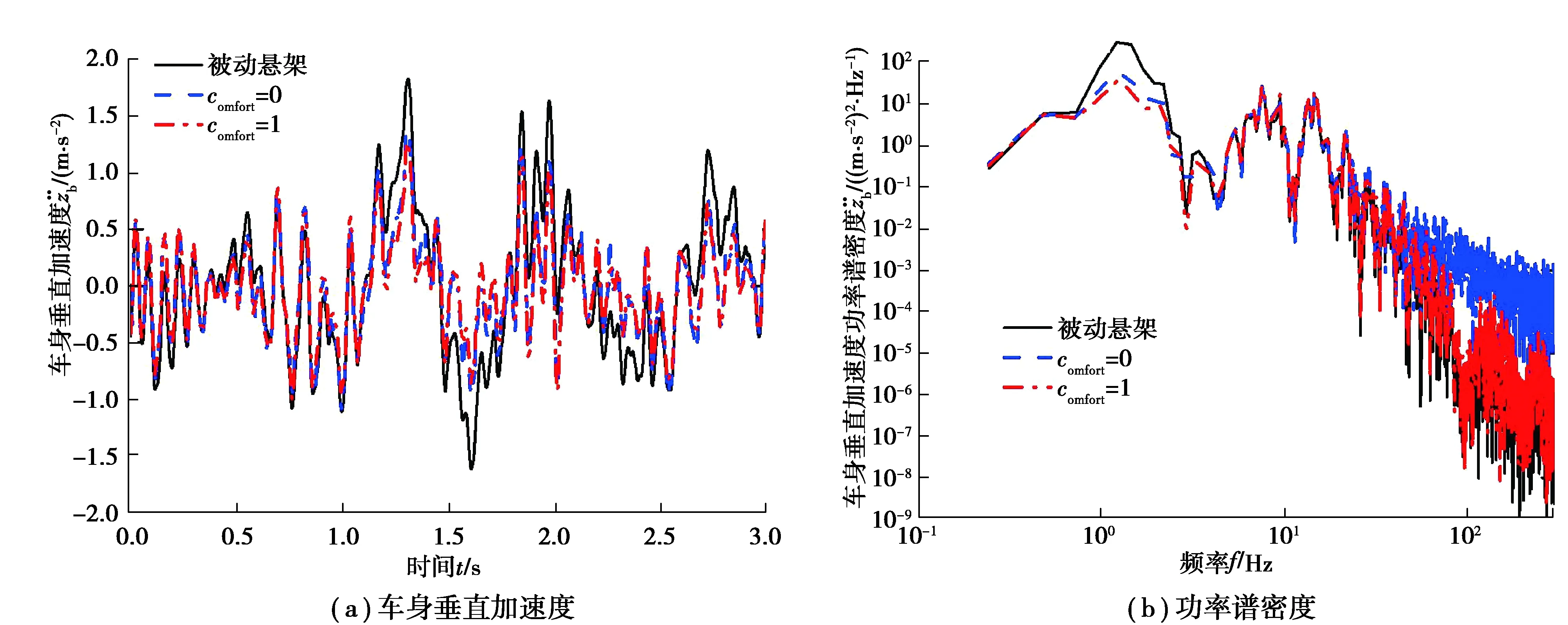
3)当fdamp与fa同向且|fa|>|fdamp|时,引入驾驶员舒适性因素comfort和切换差值Gap,舒适性因素comfort可由驾驶员调节或根据车辆行驶状态进行选择,切换差值Gap用来限制动力学性能的最大牺牲,使悬架在最大馈能情况下可以保持较好的动力学性能;如果|fa-fdamp| 4)当fdamp与fa同向,|fa|>|fdamp|且|fa-fdamp|>Gap时,悬架工作在主动模式。 在此控制策略下,对B级路面、车速为20 m/s的工况进行了仿真,仿真结果如图13~19和表4所示。基于粒子群优化的主动悬架B为未采用切换控制策略的主动悬架,此时是动力学性能最佳状态。馈能悬架comfort=1,即处于最大舒适性状态时没有牺牲动力学性能,与主动悬架的动力学性能控制效果一样。 为了便于能量回收能力的研究,在建模过程中进行了假设:所有的能量传递模式都处于理想状态;能量传递过程中没有能量损失。因此,能量回收Ere和能耗Eco可以计算如下: (11) 图13 消耗和回收能量Fig.13 Energy of consumption and regeneration 悬架回收能量与消耗能量之间的关系如图13所示。馈能悬架与主动悬架的馈能效率如图14所示。最大馈能状态和最大舒适性状态下的馈能性能比较如表3所示。 图14 馈能效率Fig.14 Ratio of total energy regeneration 从表3~4中可以看出,在最大馈能状态下,馈能悬架的回收能量接近消耗能量,回收的能量为主动悬架消耗的50.70%,与主动悬架相比牺牲了少许乘坐舒适性和平顺性;在最大舒适性状态下,馈能悬架没有牺牲动力学性能,此时与主动悬架的动力学性能控制效果一样,馈能悬架消耗的能量比回收的能量多,回收的能量为主动悬架消耗的37.58%。总的来说,车辆的能量回收能力在最大馈能状态下得到最大改善,在最大舒适性状态下最大限度地改善了车辆的动力学性能。 表3 两种状态下的馈能性能比较 表4 悬架性能均方根值对比 由图15~19中的(a)图和表3可以看出,与被动悬架相比,最大馈能状态和最大舒适性状态的馈能悬架可以显著减小车身加速度、侧倾角加速度和俯仰角加速度均方根值和峰值;与最大馈能状态相比,最大舒适性状态的馈能悬架可以更大程度地减小侧倾角加速度均方根值。从图15(b)~19(b)中可以看出,与被动悬架相比,馈能悬架在低频段获得了良好的控制效果,改善了乘坐舒适性和平顺性。 图15 车身垂直加速度及功率谱密度Fig. 15 Vehicle body acceleration and its power spectral density 图16 侧倾角加速度及功率谱密度Fig. 16 Rolling angular acceleration and its power spectral density 图17 俯仰角加速度及功率谱密度Fig. 17 Pitching angular acceleration and its power spectral density 图19 右前轮胎动行程及功率谱密度Fig. 19 Right front tire dynamic displacement and its power spectral density 基于最优控制理论设计了主动悬架LQG控制器,采用层次分析法(AHP)和粒子群优化(PSO)方法确定了性能指标的权重系数,在此基础上,提出了一种新的考虑驾驶员舒适性因素的多模式切换控制策略,通过仿真计算分析得到如下结论: 1)设计的基于粒子群优化的主动悬架LQG控制与基于层次分析法的LQG控制以及被动悬架进行仿真对比,仿真结果表明基于粒子群优化的主动悬架LQG控制能显著改善乘坐舒适性和平顺性。 2)所提出的多模式切换控制策略,在最大馈能状态和最大舒适状态下的耗能与主动悬架相比均明显减少,表明车辆的能量回收能力得到提升。同时,改善了车辆的乘坐舒适性和平顺性,提升了车辆的综合性能,实现了车辆在最大舒适状态下的最优乘坐舒适性能和在最大馈能状态下的高效能量回收性能。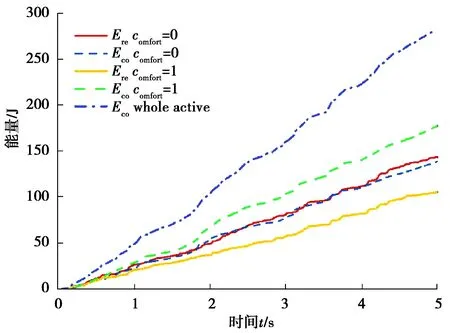



3 结 语

