初中数学教学中学生思维能力的培养

◎ 海南省万宁市新中初级中学 谢 凡

数学和数学思维的联系相当密切，一般情况下具有良好思维能力的学生学习数学时效率更高，他们能够快速掌握和应用所学知识，并从多个角度解决存在的问题。在具体的教学中，教师可结合个例教学将规律知识推导总结出来，再将其应用到其他案例中，并合理利用其他手段让学生思维能力得到锻炼。因此，教师在培养学生逻辑思维能力时要以问题为切入点，以问题的结论为依据，反推已知结果，从而高效解决问题。

初中阶段是培养学生数学思维能力的最佳阶段，在此阶段学生思维能力还处于发展时期，教师要发挥自身的作用来培养学生思维能力，并引导学生学会运用这一能力。因此，教师在数学教学中要重视培养学生思维能力，确保学生在学习中逐步形成良好的数学思维。教师在教学中要把培养学生思维能力当做核心内容，结合数形思想、动手操作和一题多解等方法激活学生思维，提高整体教学效率。

一、初中数学教学中学生思维能力培养存在的一些问题

对初中数学教学现状进行分析可知，学生思维能力培养仍然存在诸多问题，主要表现在以下几个方面：

1.教学方式落后。在课程改革深化推进背景下，教学环境发生了很大变化，若此时教师在培养学生思维能力时仍然应用传统落后的教学模式，必然很难取得理想的教学效果。在开展实践教学活动时部分老教师仍然侧重于教授解题方法，单方面地给学生灌输所学知识，讲解概念与定理，以此强化学生理解。但实际却无法凸显学生课堂主体地位，教师以自我为教学的中心，导致学生缺乏思考，不利于学生思维能力的发展。学习数学知识并非是从表面上解决问题这么简单，还需从更深层次的角度培养学生综合素养。若教师不改变落后的教学方式，只会让学生的学习变得更呆板，如此一来，学生在学习中就会盲目照搬教师灌输的解题技巧，无法把握数学的本质。

2.教学内容设置不合理。为了紧跟时代步伐，教材内容应更注重培养学生思维能力，从而提高学生数学综合能力。但是当前部分教材内容仍然比较简单，侧重于理论知识的教学，不利于教师变革教学方式，使教师在教学活动中无法注重培养学生的思维能力。

3.学生学习兴趣不浓。抽象性是数学学科比较突出的特点，且绝大多数数学概念都是运用数学公式总结抽象复杂的数学知识，这无疑增加了学生学习的难度，必然会对学生学习的积极性产生影响。若教师开展教学活动时仅注重讲解表面的知识而不深入剖析概念或定理，很容易让学生产生畏难情绪，从而阻碍学生思维能力的发展。

二、初中数学教学中学生思维能力培养的策略

具体来说，教师培养学生思维能力可从以下几个方面进行：

1.数形结合，活跃学生思维。数形结合思想是一种比较常见的思想，更是一种不可缺少的学习方法，有利于学生更好地认识数学本质，活跃学生思维。因此，在数学教学中教师要运用数形结合思想，在对比分析数与形中活跃思维，从而提高学生数学思维能力。以教学“矩形的性质与判定”为例，笔者给出一道经典例题：图1是平行四边形，其中，AQ是∠DAB的平分线、BN是∠ABC的平分线、CN是∠BCD的平分线、DQ是∠CDA的平分线，AQ和BN相交于点P，CN和DQ相交于点M，求证PQMN是矩形。

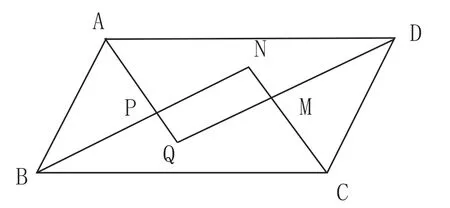
图1

在解决该问题时，为了激活学生思维，笔者应用数形结合的知识引导学生根据已知条件观察图形，并利用已知的结果进行推导。结合题目中的已知条件可以得出ABCD是平行四边形，且根据平行四边形中的邻角互补可以判断出相邻内角平分线互相垂直。之后以角平分线、三个角都是直角判断该图形为矩形。如此，学生在教师的引导下观看图形和题意，探索题目中已知和未知条件，并运用数形结合思想展开思考，从而不断提高自身学习数学学科的水平。

2.动手操作，激活学生主动思维。教师在初中数学教学中要以学科特点为基础，加强学生动手操作的能力，让学生在学习的过程中亲身经历探索的过程，帮助其解决问题，引导学生主动思考。以教学“相似三角形”这部分内容为例，考虑到部分学生无法理解本节课的概念，因此笔者根据问题情境引导学生动手操作，让其亲自经历问题的分析、建模和解决等过程，形成主动思维。比如说“假设周末小军和爸爸去公园散步，阳光照射过来时小军和爸爸的影子分别为120cm、144cm，爸爸的身高是175cm，小军的身高是多少呢？”通过这个问题结合相关的问题情境引导学生分析问题，最后借助“同一时刻的高和影子长”构成了相似三角形，解决这一问题。学生在解决问题的过程中产生了主动思维，对其学习数学学科起到良好的促进作用。

3.一题多解，拓宽学生思维。数学学科中一题多解是相当重要的教学方式，不断优化解题思路，有利于学生从内容、视角等方面分析，从而拓宽学生思维。因此，为了培养学生思维能力，教师在教学中要合理利用一题多解，引导学生从多个角度分析题目，从中掌握科学的学习方法，不断提高其学习能力。比如教学“反比例函数”这部分内容时，针对“y与z成反比例，z与x成反比例，其中，z=3，y=4，求关于x的函数解析式。”这道题，笔者让学生求出y关于x的函数解析式。第一种解法：先假设y=kz，因为k为常数，所以k≠0，就有4=3k，因此k=4/3，y=4z/3；设z=m/x，m≠0，因此m=12，z=12/x，因此y=kz=4/3×12/x=16/x。第二种解法可以假设y=k1z，z=k2/x，带入公式得y=k1k2/x，最后带入x和y值得出k1k2=-16，最后求出y=16/x。引导学生学会从不同的角度思考问题，在一题多解中形成良好的思维，能不断提高其综合解题能力，促进学生形成发散思维。

4.启发教学，培养学生思维品质。初中阶段的数学教学需要教师优化教学方式，以学生学习情况与教学目标为基础开展教学。首先，教师制定教学目标时应以学生认知水平以及实际情况为基础，加大力度培养学生思维能力。其次，不断优化教学策略，从学生的角度应用启发式教学，避免学生思维固化。因为初中阶段教材中包含的知识点较多且复杂抽象，教师应用启发教学可以促使学生全面了解数学概念的内涵，从而提高学生思维品质。此外，启发学生是应用启发式教学的关键，教师要创设丰富的教学情境调动学生学习的积极性，让学生更好地分析与理解数学问题的本质。

5.动脑思考，培养学生发散思维。“学而不思则罔，思而不学则殆。”学习必须勤于思考，这是学好各个学科的关键，但是很多学生在学习数学学科时受到思维模式的限制，发散性思考不足，面对数学题时无从下手，无法找到解决问题的思路。由此可见，教师应引导学生思考数学问题，拓宽学生思维，让学生从以往单一思维向丰富立体的思维转变。如解决“求x2+5x+6=(x-2)2+A(x-2)+B的参数A与B的取值”这一问题时，教师可以让学生分别从取特殊值法、配方法两个角度分析题目。首先，试用取特殊值法求解，让x=0，x=2，则可以得出22+5×2+6=（2-2）2+A×（2-2）+B，从而计算出B=20。若x=0,则可以计算出6=4-2A+B，最终计算出A=9，B=20。其次，用配方法求解，也就是将方程的左边配方，得出x2+5x+6=(x-2)2+9(x-2)+20，通过对恒等式两边的系数进行观察最终可以计算出A=9，那么B=20。结合上述问题的解决方法可知，对于运用恒等式及其变形的相关规律求解问题，学生掌握数学思想后就可以快速找到相应的解决方法。

在初中阶段的数学教学中，教师开展教学活动若只关注公式和概念的学习，不注重培养学生空间建模等思维能力，则不利于学生理解所学内容。所以，课程改革深化推进背景下，教师要注重发展学生素质，加强数形结合思想的应用，引导学生动手操作，通过一题多解等方法培养学生思维能力，让学生在学习中掌握更多数学知识，培养其主动思考和应用能力，发展其数学思维，促进学生全面发展。