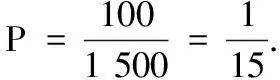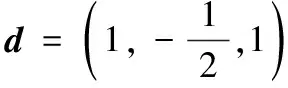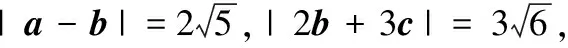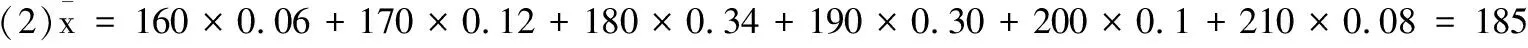高二数学测试

一、单项选择题(本大题共8小题，每小题5分，计40分)

1. 甲、乙、丙三人到三个景点旅游,每人只去一个景点,设事件A为“三个人去的景点不相同”,事件B为“甲独自去一个景点”,则概率P(A|B)等于( )

2.已知空间三点O(0，0，0)，A(-1，1，0)，B(0，1，1)，在直线OA上有一点H满足BH⊥OA,则点H的坐标为( )

(C)(-2,2,0) (D)(2,-2,0)

3.2020年东京夏季奥运会设置4×100米男女混合泳接力这一新的比赛项目,比赛的规则是:每个参赛国家派出2男2女共计4名运动员比赛,按照仰泳→蛙泳→蝶泳→自由泳的接力顺序,每种泳姿100米且由一名运动员完成,每个运动员都要出场,中国队确定了备战该项目的4名运动员名单,其中女运动员甲只能承担仰泳或者自由泳,男运动员乙只能承担蝶泳或自由泳,剩下的男女各一名运动员则四种泳姿都可以上,那么中国队共有布阵的方式( )

(A)6种 (B)12种

(C)24种 (D)144种

(A)(1，-1，1) (B)(-1,1,1)

(C)(1,-1,2) (D)(-1,1,2)

(A)(1,1,1) (B)(-1,1,1)

(C)(1,-1,1) (D)(1,1,-1)

7.某高中期中考试需要考查九个学科(语文、数学、英语、生物、物理、化学、政治、历史、地理),已知语文考试必须安排在首场,且物理考试与英语考试不能相邻,则这九个学科不同的考试顺序共有( )种

8.如图,在平行六面体ABCD-A1B1C1D1中，AB=1，AD=1，AA1=1,∠BAD=90°，∠BAA1=∠DAA1=60°，则线段AC1的长为( )

二、多项选择题(本大题共4小题,每小题5分,计20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)

9.为了解目前全市高一学生身体素质状况,对某校高一学生进行了体能抽测,得到学生的体育成绩X～N(70，100),其中60分及以上为及格,90分及以上为优秀,则下列说法正确的是( )

附:若X～N(μ,σ2),则P(μ-σ≤X<μ+σ)=0.682 6,P(μ-2σ≤X<μ+2σ)=0.954 4

(A)该校学生体育成绩的方差为10

(B)该校学生体育成绩的期望为70

(C)该校学生体育成绩的及格率不到85%

(D)该校学生体育成绩的优秀率超过4%

10.已知空间中三点A(0，1，0)，B(2，2，0)，C(-1，3，1)，则下列说法不正确的是( )

(D)平面ABC的一个法向量是(1，-2，5)

11.下列问题中是排列问题的是( )

(A)从甲、乙、丙三名同学中选出两名分别参加数学、物理兴趣小组

(B)从甲、乙、丙三名同学中选出两人参加一项活动

(C)从a,b,c,d中选出3个字母

(D)从1,2,3,4，5这五个数字中取出2个数字组成一个两位数

12.下列说法正确的是( )

(A)点P(-1，2，3)关于xOy平面对称的点的坐标是P(1，-2，3)

(B)若{a,b,c}为空间中一组基底,则{a+b,a-b,c}可构成空间另一组基底

三、填空题(本大题共4小题,每小题5分,计20分)

14.空间直角坐标系中,两平面α与β分别以n1=(2,1,1)与n2=(0,2,1)为其法向量，若α∩β=l,则直线l的一个方向向量为______.(写出一个方向向量的坐标)

15.假设某次数学测试共有20道选择题,每题都给了4个选项(其中有且仅有一个是正确的).评分标准规定:每题只选1项,答对得5分,否则得0分.某考生每道题都给出了答案,并且会做其中的12道题,其他试题随机答题,则他的得分X的方差D(X)=______.

四、解答题(本大题共6小题,计70分.解答应写出文字说明、证明过程或演算步骤)

17.(本小题满分10分)已知向量a=(1,1,0),b=(-1,0,2).

(1)若(a+kb)∥(2a+b)，求实数k;

(2)若向量a+kb与2a+b所成角为锐角，求实数k的取值范围.

18.(本小题满分12分)已知1 500件产品中有100件不合格品,从中抽取15件进行检查,用随机变量X表示取出的15件产品中不合格品的件数.试求:

(1)X的分布列;

(2)X的均值E(X).

19.(本小题满分12分)已知向量a=(2,1,-2),c=(-1,0,1),若向量b同时满足①a·b=-1;②|b|=3;③b与c垂直.

(1)求向量b的坐标；

20.(本小题满分12分)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,∆PAD是等腰三角形,AB=2AD，E是AB的一个三等分点(靠近点A)，CE与DA的延长线交于点F，连结PF.

(1)求直线PD与EF所成角的余弦值；

(2)求二面角A-PE-F的正切值.

21.(本小题满分12分)当前,以“立德树人”为目标的课程改革正在有序推进.高中联招对初三毕业学生进行体育测试,是激发学生、家长和学校积极开展体育活动,保证学生健康成长的有效措施.郑州市2018年初中毕业生升学体育考试规定,考生必须参加立定跳远、掷实心球、1分钟跳绳三项测试,三项考试满分为50分,其中立定跳远15分,掷实心球15分,1分钟跳绳20分.某学校在初三上期开始时要掌握全年级学生每分钟跳绳的情况,随机抽取了100名学生进行测试,得到下边频率分布直方图,且规定计分规则如下表:

每分钟跳绳个数[155,165)[165,175)[175,185)[185,+∞)得分17181920

(1)现从样本的100名学生中，任意选取2人，求两人得分之和不大于35分的概率；

(2)若该校初三年级所有学生的跳绳个数X服从正态分布N(μ,σ2)，用样本数据的平均值和方差估计总体的期望和方差，已知样本方差S2≈169(各组数据用中点值代替).根据往年经验，该校初三年级学生经过一年的训练，正式测试时每人每分钟跳绳个数都有明显进步，假设今年正式测试时每人每分钟跳绳个数比初三上学期开始时个数增加10个，现利用所得正态分布模型：

(i)预估全年级恰好有2 000名学生时,正式测试每分钟跳182个以上的人数;(结果四舍五入到整数)

(ii)若在全年级所有学生中任意选取3人,记正式测试时每分钟跳195个以上的人数为ξ，求随机变量ξ的分布列和期望.

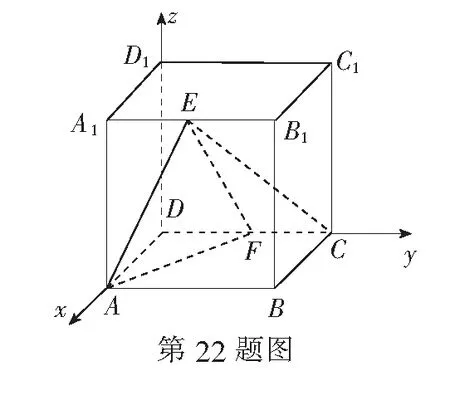
附：若随机变量X服从正态分布N(μ,σ2),则P(μ-σ

P(μ-2σ

P(μ-3σ

22.(本小题满分12分)在棱长为2的正方体ABCD-A1B1C1D1中，E，F分别为A1B1,CD的中点.

(2)求直线EC与AF所成角的余弦值；

(3)求面AFE和面AFB夹角的余弦值.

参考答案

一、单项选择题

1.C;2.B;3.A;4.D;5.B;

6.A;7.C;8.C.

二、多项选择题

9.BC;10.ABC;11.AD;12.BC.

三、填空题

四、解答题

(2)因为a+kb与2a+b所成角为锐角，所以由(1)可得(a+kb)·(2a+b)=(1-k,1,2k)·(1,2,2)=1-k+2+4k>0,解得k>-1.

X01…k…15PC015×1415()15C115×115()×1415()14…Ck15×115()k×1415()15-k…C1515×115()15

又σ2≈169,σ=13,所以正式测试时，μ=196，σ=13,得μ-σ=182.

(ii)由正态分布模型，从全年级所有学生中任取1人，每分钟跳绳个数195以上的概率为0.5,即ξ～B(3,0.5).

ξ0123P0.1250.3750.3750.125

E(ξ)=3×0.5=1.5.

22.建立如图所示的空间直角坐标系，则题设点A(2，0，0)，F(0，1，0)，C(0，2，0)，E(2，1，2).

(1)由CE=(2，-1，2)，得

(3)平面AFB的一个法向量为n1=(0,0,1).