薄板类零件加工精度可靠性分析及工艺参数优化

易 茜 李聪波 潘 建 张 友

重庆大学机械传动国家重点实验室，重庆，400044

0 引言

制造技术的发展对零件的加工质量提出了越来越高的要求。薄板类零件因具有结构紧凑、质量小、强重比高等优点，而被广泛应用于航空航天、汽车以及军工等领域。然而，此类零件有着厚度小、刚度低等突出特点，在制造过程中容易产生较大的加工变形，由此导致的较大加工误差使工件厚度不均匀甚至尺寸超差，从而降低了产品的使用性能和加工效率[1]。因此，研究并优化薄板类零件的加工变形具有重要意义[2]。

国内外学者对薄板类零件的加工变形误差优化控制进行了大量的研究。一部分学者通过建立加工误差预测模型实现加工变形误差补偿。例如，GE等[3]将在机测量(on machine measurement, OMM)技术应用于综合加工误差的测量和加工变形误差建模，并实现了薄腹板件实时加工误差补偿；RATCHEV 等[4]建立了带有加工变形的铣削加工有限元模型，在此基础上，结合切削力仿真和镜像补偿法修正切削轨迹，实现了加工变形误差补偿；LI等[5]提出了一种基于加工面与设计面差值的侧铣削变形误差计算方法，并利用刀具轨迹修正法对侧铣削变形误差进行补偿;陈蔚芳等[6]建立了一种快速仿真平台，考虑力与变形的耦合关系，实现了加工变形的主动补偿。

上述研究基于加工变形预测模型，并利用实时误差补偿手段达到控制加工误差的目的,然而，补偿手段大多通过修改刀具轨迹(G代码)实现。在生产实际中，刀具轨迹修正非常复杂且不稳定，尤其对于多轴加工，大量代码需要被修改[3],因此，一些学者通过优化工艺参数实现加工变形误差的控制。例如，CHENG等[7]运用响应面法和人工蜂群算法对薄壁件加工工艺参数进行优化，有效地改善了工件加工变形和表面质量，提高了加工精度；GAO等[8]对切削参数和刀具路径进行优化，减小了薄板类零件的加工变形误差；胡权威等[9]提出了一种有限元正交优势分析方法，用以优化铣削参数，减小铣削产生的零件变形；曾莎莎等[10]提出了一种倒传递神经网络算法，对薄壁件铣削加工工艺参数进行优化，改善了加工质量。上述研究大多通过切削参数优化设计使加工变形误差得到有效控制。然而，改变进给速度、切削深度等参数可能会导致加工效率降低，并且加工过程中由于机床运动误差等不确定性因素影响，可能导致工艺参数最优组合落入失效区，无法满足期望的加工精度可靠度。

综上所述，本文考虑工件加工变形动态误差以及机床运动误差等不确定性因素，开展薄板类零件加工精度可靠性分析和铣削加工工艺参数优化设计。

1 薄板类零件加工变形分析及预测建模

1.1 加工变形分析

切削加工过程的实质是加工系统中各部分之间力和刚度的较量，若刀具刚度差，切削力较大，则刀具易产生弯曲变形。在薄板件加工过程中，由于工件自身的弱刚性以及较小的切削深度，切削力会引起工件变形，而刀具变形相对不大[6]。

图1为一典型薄板类零件的加工示意图，由弹性变形原理可得任意一点C产生的加工变形Y，表示为

图1 薄板类零件

Y=F/KC

(1)

其中，F为铣削力，薄板类零件的变形主要由Z向铣削力引起，在工艺条件确定时主要由工艺参数决定；KC为刚度，与工件弹性模量、C点自身位置以及工件的设计尺寸a、b、h有关。

切削加工是一个动态过程，加工位置可以被表示为关于加工时间的函数，即p(t)={x(t),y(t)}。另外，对于特定零件的加工过程，材料属性是确定的，工件设计尺寸也为定值，其实际厚度主要受轴向切削深度影响，因此，加工变形量Y可以表示为工艺参数S(S=(n,f,ap,ae),n为主轴转速，f为进给速度，ap为轴向切削深度，ae为径向切削深度)和加工位置p(t)的函数。然而，加工过程中的材料去除效果导致很难通过理论推导获得具体数学模型[11-12]，因此，本文结合有限元法和高斯过程回归模型对薄板件加工变形进行预测。

1.2 加工变形预测模型的建立

本节基于有限元法和高斯回归过程进行加工变形预测，主要有两个关键步骤：①进行仿真切削实验，以获得工件在不同工艺参数组合下的实际变形分布；②利用高斯过程回归算法建立不同工艺参数组合下的加工变形预测模型。

1.2.1基于有限元的切削加工仿真

采用ABAQUS仿真分析软件实现切削力的动态加载、材料的动态去除、节点位移的自动提取等功能。仿真过程如图2所示，具体步骤如下：首先，建立薄板工件的几何模型，定义分析步骤、装夹载荷以及边界条件；其次，为模型划分合适的工件网格；然后，利用机理模型构建出铣削参数与铣削力的关系，进一步计算出瞬时铣削力并动态加载在待去除单元相应节点上；随后，采用生死单元技术[13]模拟物料的动态移除，使待移除单元失效；最后，自动提取并处理不同时刻下加工位置的节点位移，从而得到工件加工变形分布。

图2 薄板件切削仿真流程

为保证有限元分析模型的计算精度，一方面选择计算性能较高的六面体单元进行网格划分，并通过网格独立性测试确定有限元模型的最优网格数;另一方面，采用精度较高的圆柱螺旋立铣刀模型[11]计算瞬时铣削力，运用辨识试验对铣削力经验模型的系数进行实验标定，以提高瞬时铣削力的预测精度，进一步提高有限元模型计算精度。

1.2.2基于高斯过程的加工变形预测

利用仿真数据，并结合高斯过程回归来描述工艺参数、加工位置和加工变形之间的关系，加工变形量预测模型可以表示为

Y(S,p(t))=g(n,f,ap,ae,p(t))Tw+ε

(2)

将工艺参数对应各时刻下的加工变形作为训练样本，Dtrain=(Xtrain,Ytrain)=((S,p(t))train,Ytrain)，测试集Dtest=(Xtest,Ytest)。Dtrain与Dtest服从联合高斯分布，由此可得输入为Xtest时加工变形分布模型：

(3)

式中，K为学习样本的协方差矩阵；K0为学习样本Xtrain与输入样本Xtest之间的协方差矩阵；K00为输入样本Xtest自身的方差。

2 薄板类零件加工精度可靠性分析

加工精度可靠性是指数控机床在规定条件下和规定时间内，加工工件达到期望加工精度的能力[14]。薄板类零件的加工变形使得零件加工精度可靠度下降明显，无法满足使用要求,因此，建立综合考虑加工变形及机床运动误差的可靠性模型是亟需解决的问题。

2.1 加工精度可靠性建模

机床的误差建模是分析加工精度可靠性的前提，本文基于多体系统运动学假设和齐次坐标变换法，综合考虑加工变形动态误差以及数控机床运动误差，建立加工精度可靠性模型。图3所示为某AC型五轴数控机床的拓扑结构，其两条运动传递链分别为“0—1—2—3”，“0—4—5—6—7—8”。

0.床身 1.A轴 2.C轴 3.工件 4.X轴 5.Y轴 6.Z轴 7.主轴 8.铣刀

为构建运动误差传递方程，将机床床身坐标系作为参考系，用O0表示。主轴坐标系O1相对于O0的偏移矢量P1=(x1,y1,z1)T；刀具坐标系设置在刀具下端中心点O2,相对于O1的偏移矢量P2=(0,0,z2)T；工件坐标系相对于O0的偏移矢量P3=(x3,y3,z3)T；设X、Y、Z、A、C轴的运动误差分别为ΔxX、ΔyY、ΔzZ、ΔβA、ΔβC，对应的初始运动位置分别为x0、y0、z0、a0、c0。则机床相邻单元件的运动变换方程为

(4)

薄板件的加工变形使得加工精度存在不确定性，因此，引入加工变形误差Y(S,p(t))。当工艺方案确定时，Y(S,p(t))与加工艺参数S=(n,f,ap,ae)T和加工位置p(t)有关。在薄板件加工过程中，加工变形将影响Z向的加工精度。如图4所示，若刀具坐标系下的理论刀具接触点为(x,y,z)T，则实际接触点Pt=(x,y,z-Y(S,p(t)))T。设工件坐标系下的刀具接触点Pw=(x′,y′,z′)T，由此可得机床加工误差:

图4 加工变形示意图

(5)

由于薄板件的加工精度主要受机床Z向加工误差的影响，故求解式(5)可得薄板件加工误差模型EZ：

EZ=x3(sina0-ΔβAcosa0)(sinc0+ΔβCcosc0)+

x′(-ΔβAcosa0+sina0)(ΔβCcosc0+sinc0)+

y3(sina0-ΔβAcosa0)(cosc0-ΔβCsinc0)+

y′(-ΔβAcosa0+sina0)(-ΔβCsinc0+cosc0)+

z3(cosa0+ΔβAsina0)+Y(S,p(t))-ΔzZ-z+

z′(cosa0+ΔβAsina0)-z1-z2-z0

(6)

设工件加工工艺允许的最大加工误差为E0，可以推导出薄板件的加工精度可靠性模型：

E(X,Y(S,p(t)),t)=E0-|EZ|

(7)

X=(ΔzZ,ΔβA,ΔβC)T

2.2 加工精度可靠性模型求解

根据时变可靠性理论，失效事件发生在极限状态函数大于任何时间节点的阈值时刻[15]。在时间[t0,tm]内，薄板件的加工精度模型失效率为pf(t0,tm)，因此，加工精度可靠度

R(t0,tm)=1-pf(t0,tm)=

P{E(X,Y(S,p(t)),t)≥0,∀t∈[t0,tm]}

(8)

式中，P{·}表示概率。

本文运用基于单循环Kriging代理模型(a single-loop Kriging, SILK)的时变可靠性分析法[16]求解上述薄板件加工精度可靠性模型，主要步骤如下：①加工变形量离散化。Y(S,p(t))可以被看成一个随机过程，在进行时变可靠性分析之前，通过K-L展开[17]将其表示为独立随机变量Z。②建立加工精度可靠性求解代理模型。首先，从样本空间生成初始训练点Din=(Xin,Zin)，计算对应点的响应值；然后，采用蒙特卡罗模拟(Monte Carlo simulation, MCS)求解加工精度可靠性。③训练代理模型E′(·)，通过下式判断R(t0,tm)计算精度是否满足设定要求：

(9)

式中，fCOV为评价指标；NM为蒙特卡罗抽样次数。

当R(t0,tm)计算精度小于预期值时则更新初始样本点Din,并重新训练E′(·)，重复此过程直到满足收敛条件。

3 薄板类零件铣削加工工艺参数优化

为实现薄板零件加工的高精度、高效率加工，建立以加工时间与薄板件加工平均变形量为目标、期望加工精度可靠度为约束条件的铣削加工工艺参数优化设计模型，以获得最优工艺参数组合。

3.1 多目标优化模型

3.1.1优化变量

将影响加工效率、加工质量和刀具寿命的工艺参数(主轴转速n、进给速度f、轴向切削深度ap以及径向切削深度ae)作为薄板件铣削加工工艺优化的设计变量。

3.1.2优化目标

(1)加工时间t。加工时间t由材料去除体积V和材料去除率MV决定，其中，MV由进给速度f、轴向切削深度ap和径向切削深度ae决定。若待加工薄板件的尺寸为a×b×h，对于一道既定工序，加工余量可根据切削深度ap进行调整，要求一次走刀完成加工，则材料去除面积为固定值A，且A=ab[18]。因此，优化目标t可以表示为

(10)

(2)平均变形误差Ym。加工平均变形Ym与工艺参数、工艺条件以及工艺方案相关。在实际加工中，当工艺方案和工艺条件确定时，加工变形误差主要由工艺参数决定，因此，优化目标Ym可表示为

(11)

其中，ti代表第i个加工时刻，共N个采样点。

3.1.3约束条件

薄板件铣削加工工艺参数的选择需要满足加工精度可靠性的要求。除此之外，加工过程是在确保数控机床加工零部件质量和自身性能的前提下进行的，需要满足包括主轴转速、进给速度、切削深度、切削宽度、机床功率等多种工艺条件，因此，优化变量应满足以下约束。

(1)时变可靠性约束如下：

式中，Rmin为加工过程中最小允许的加工精度可靠度。

(2)工艺条件约束如下：

nmin≤n≤nmaxfmin≤f≤fmax

ap，min≤a≤ap，maxae，min≤a≤ae，max

Pc≤ηPc,maxFc≤Fc,max

式中，nmin、nmax分别为数控机床铣刀所允许的最小与最大转速；fmin、fmax分别为数控机床所允许的最小与最大进给速度；ap，min、ap，max分别为数控机床所允许的最小与最大轴向切削深度；ae，min、ae，max分别为数控机床所允许的最小与最大径向切削深度；η为数控机床功率的有效系数；Pc，max为数控机床额定功率；Fc，max为数控机床的最大切削力。

基于上述分析，薄板件铣削加工工艺参数优化设计数学模型表示如下：

(12)

3.2 优化模型求解

以加工精度可靠性为约束的优化设计是一个双循环计算过程，包括外循环的优化寻优过程与内循环的可靠性分析。多目标水循环算法(multi-objective water cycle algorithm, MOWCA)作为一种新的元启发式优化算法，在求解多目标优化问题上有着较高的计算效率及求解精度[19]，因此，本文引入MOWCA对优化过程进行求解，并利用SILK时变可靠性分析方法对薄板件加工精度可靠性进行评估。

每次迭代求解中，需要求解当前解集中各初始解对应的可靠性约束。首先, 利用高斯过程回归模型获得加工变形量Y；其次，将加工位置坐标转用加工时间表征，并将加工变形量转换为独立随机变量Z；然后，结合机床加工误差训练代理模型E′(·)，若不满足精度要求，更新样本重新训练，直至满足要求；最后，求解得到各时刻对应的时变可靠性约束函数R(0,ti)，用于检验当前解集中各个体是否满足时变可靠性以及加工条件的要求。

综上所述，本文基于SILK时变可靠性分析法和MOWCA对加工工艺参数进行优化设计的具体求解流程如图5所示。

图5 算法求解流程图

4 案例研究

为验证所提方法的有效性，设计了典型薄板件加工实例。如图6所示，实验设备是MAZAK VARIAXIS j-500/5型五轴数控机床，其基本参数为：额定功率11.5 kW，功率有效系数0.8；对应的刀具直径为10 mm，螺旋角为30°，材料为硬质合金，齿数为4齿；待加工工件尺寸a×b×h=70mm×32mm×5 mm，加工面积2240 mm2，材料为ZL114A，弹性模量71 GPa，泊松比0.33；加工过程采用“Z字形”走刀，刀具轨迹如图7所示。由于建立加工变形量预测模型需要大量的训练数据，通过实验法获得十分昂贵，不利于工程实践,因此，运用ABAQUS进行切削仿真，建立加工变形预测模型，并进行加工精度可靠性分析,然后，开展工艺参数可靠性优化设计,最后，利用加工实验验证所得优化结果的有效性。

图7 加工工件图

为准确预测瞬时铣削力数值,开展铣削力实验以求得铣削力模型[9]的系数。实验结果如下：①剪切作用对切向、径向和轴向切削力的作用系数值分别为Ktc=747.3 N/m2，Krc=152.5 N/m2，Kac=209.7 N/m2；②各向刃口力系数值分别为Kte=22.30 N/m，Kre=20.2 N/m，Kae=1.36 N/m。由此得出不同工艺参数下的瞬态铣削力，实现切削载荷准确加载。

在加工过程中，主轴转速n、进给速度f、轴向切削深度ap及径向切削深度ae均可变，为保证每次实验走刀路径一致，本节将ae设置为8 mm，将n、f、ap作为实验可控因素。首先，选择L16(43)正交表试验法安排仿真实验，各因素水平如表1所示;然后，建立有限元模型并动态加载切削载荷，进行切削仿真并提取每组工艺参数下加工变形随加工位置的动态分布数据。其中，各组切削仿真实验都加工到设计尺寸5 mm，零件两端面非加工区域由刚性面固定，两端底部平面由专用垫块支撑。另外，通过静态应变仪测得实际夹具夹持应力约为0.75 MPa，并将其作为边界条件考虑到分析过程中。

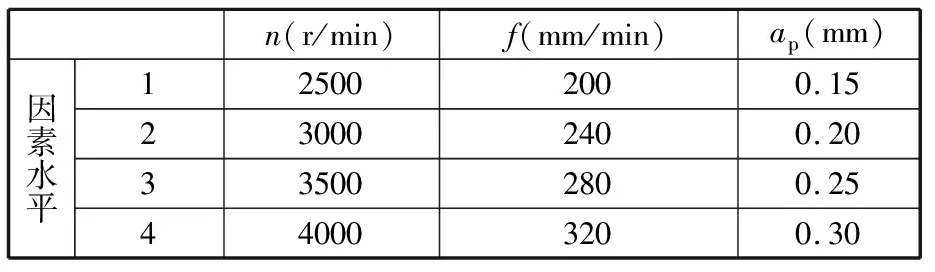
表1 仿真实验各因素水平

4.1 加工变形预测结果

表2列出了各组实验参数下加工变形量的均值和最大值，基于此，利用MATLAB 软件编程训练高斯过程回归预测模型。为保证高斯过程回归模型的训练效果，用于模型的训练数据共1216条，包含16组工艺参数，每组参数包含走刀路径上的76个样本点。另外，为验证加工变形误差模型预测精度，将n=3800 r/min,f=220 mm/min,ap=0.17 mm的仿真实验数据作为验证数据集，共76个样本点。预测值和仿真值对比结果如图8所示，仿真实验值与模型预测值变化趋势一致，且均分布在95%置信区间内，表明该模型对加工变形有较好的预测效果。

表2 各组参数下加工变形量的均值和最大值

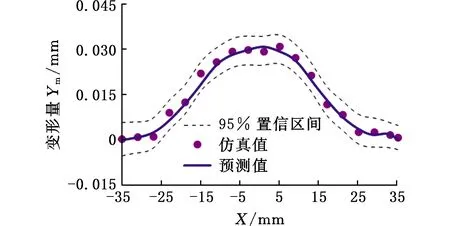
(a)切削路径Y=-13 mm

4.2 加工精度可靠性分析

根据实验数控机床的结构参数，该机床各单元相对于参考坐标系的偏移量P1=(-100.102,-35.258,308.901)T，P2=(0,0,168.451)T，P3=(-22.561,-15.258,150)T；刀位点坐标Pt=(0,0,0)。根据确定的工艺方案确定工件坐标系下刀具运动轨迹p(t)为xw=f[mod(t,70/f)]-36.021,yw=ae[t(70/f)]-13，zw=-ap(mod为取余运算，为取商运算符)。允许工件在Z向的加工误差为0.040 mm；机床的各项运动误差分布为ΔxX～N(0,0.001 252),ΔyY～N(0, 0.001 412),ΔzZ～N(0, 0.001 682),ΔβA～N(0, 0.000 0122),ΔβC～N(0,0.000 0122)。基于上述条件并结合式(11)可求得加工精度可靠性模型。

将加工位置转换为加工时间表征，并基于Kriging时变可靠性分析模型，计算工艺参数组合为n=3800 r/min,f=220 mm/min,ap=0.17 mm时的加工精度可靠度变化曲线，结果如图9所示。

图9 加工精度可靠度变化曲线

由图9可知，加工变形量随加工时间变化呈现出波动较大的变化规律，这是由不同加工位置的刚度不同导致的。显然，加工精度可靠度从第66.4 s开始下降，并且随着加工时间积累逐渐降低；当加工变形达到一定程度时，可靠度急剧下降，t=70.1 s时可靠度仅为94.4%，难以保证加工质量。由此可见，加工变形对薄板件的加工精度可靠度影响十分显著，因此，需要对加工变形进行优化控制，以满足预期加工精度可靠度。

4.3 工艺参数优化设计结果分析及实验验证

4.3.1工艺参数优化设计结果及分析

利用MATLAB软件编写求解算法，多目标水循环算法的参数设置如下：河流和海洋总数Nsr=50,参数dmax=0.0012, 种群规模Npop=150，迭代次数设置为100，Pareto解集Npa=20;允许最小加工精度可靠度设置为Rmin=97%。求解后，所得较优工艺组合和优化结果如表3所示。其中，综合优化方案为综合考虑平均加工变形的多目标优化，仅优化效率方案和仅优化变形为单目标优化，经验方案为根据车间工艺人员的经验进行确定。

表3 优化结果

由表3可知，仅以加工效率(加工时间)为优化目标时，较大的切削用量使得材料去除率增加，从而缩短了加工时间，但大的切削用量会使切削力增大，从而加剧了工件的加工变形，使得加工误差增大。仅以平均加工变形量为优化目标时，平均加工变形下降了23.81%，但加工时间增长了39.47%。由此可见，单一优化加工过程的平均变形或效率的方案均有弊端。本文在满足加工精度可靠度要求的前提下，通过平衡加工变形、加工效率两个目标，在减小加工变形量时，尽可能缩短加工时间。

综合考虑加工变形和加工效率时，虽然比仅优化效率的加工时间增长了9.56%，但平均变形量减小了6.12%，同样，虽然与仅优化变形相比，其平均加工变形增大了23.21%，但加工时间减短了21.45%；与经验方案相比，综合优化使平均加工变形减小了21.14%，加工效率提高了4.18%。图10所示为综合优化、优化效率和经验方案的加工变形分布。由图10可知，经验方案的最大加工变形为0.0399 mm，而综合优化方案的最大加工变形为0.0323 mm，减小了18.80%。因此，经综合优化后可显著改善加工变形。

(a)切削路径Y=-13 mm

图11所示为各方案下加工可靠度变化曲线。由图11可知，经验方案的可靠度超过了期望的最低加工精度可靠度，难以保证加工质量；仅优化加工效率的最低加工精度可靠度为97.12%，虽然满足期望加工精度可靠度要求，但仅高出期望最低值0.12%，可靠性裕度较小；而综合优化方案最低加工精度可靠度达到了98.21%，与仅优化变形相比虽然略有下降，但仍有较大裕度。综上所述，综合优化方案要优于仅优化效率、仅优化变形以及经验方案，实现了加工平均变形与加工效率的协调最优。

图11 不同方案下加工精度可靠度变化曲线

4.3.2优化结果验证

为验证优化结果的可靠性，利用表3方案1和方案4的工艺参数组合进行了实验验证。加工完成后，采用三坐标测量仪测量，测量现场如图12所示。测量过程中，沿着加工路径每隔4 mm 进行采样，共计76个采样点，与仿真过程保持一致。然后计算所有采样点的平均值，最终结果如表4所示。

表4 仿真与实验结果的对比

图12 加工误差测量现场

结果表明，实测量小于仿真条件获得的变形量。一方面由于加工完成后的变形测量值实际是无切削力状态下的塑性变形(残余变形)，而不是加工过程状态下的实际变形误差；另一方面，实验中的测量误差、刀具误差也会导致实验结果存在偏差。总体而言，两组实验结果相对误差均在10%左右，可以认为仿真结果能较为准确地反映真实加工变形误差。

5 结论

(1)本文分析了薄板件铣削加工过程中的加工变形，基于有限元法和高斯过程回归算法建立了加工变形预测模型。基于此，建立了考虑工件加工变形和机床运动误差的加工精度可靠性模型，对不同加工时刻的加工精度可靠度进行了评估。

(2)建立了以加工效率和平均加工变形为目标、加工精度可靠度以及加工工艺条件为约束的工艺参数优化模型，并利用多目标优化算法进行求解。结果表明，综合优化可有效减小薄板件加工平均变形并提高加工效率，实现加工变形和加工效率的协调最优。

本文在进行薄板类零件工艺参数优化设计时只考虑了工件的弹性变形，因此，如何综合考虑刀具变形开展薄板件工艺参数优化设计将是下一步的研究重点。