基于风险效益平衡的混凝土坝寿命评估理论及其应用

姚 虞，武明鑫，周兴波，杨娟丽

(1.水电水利规划设计总院，北京 100120；2.中国水利电力对外有限公司，北京 101199)

0 引 言

目前，我国拥有不同规模的水坝超过9.8万座，是世界上拥有水坝最多的国家，水库大坝为我国经济社会发展发挥了重要作用。然而，我国有超过4万座大坝被评定为病坝[1]，每年都需要大量的资金和人力进行加固除险。我国以前水电工程建筑物设计较少考虑耐久性问题，常常由于耐久性不足，增加运行过程中的修理与加固费用，影响或者限制建筑物功能或寿命；缺少相应的管理和控制体系，不能有效评价工程长期运行安全。另外，我国学术界对大坝寿命评估基础理论和关键科学问题方面研究较少，工程领域亦无成熟的工程寿命评估行业标准或技术导则。这一实际情况与我国水利水电行业快速发展形成了鲜明对比，因此，亟需加强在工程寿命评估以及相应对策措施方面的科学研究。在我国水电建设的逐渐退潮、水电开发进入“新常态”的大背景下，开展大坝寿命评估研究恰逢其时，对水电工程的安全管理和永续利用的意义重大。

目前国内外研究主要集中在材料和结构构件的耐久性上，比如(钢筋)混凝土材料、预应力结构等，在此方面取得大量成果[2-5]。然而，水电工程的寿命与其设计、材料、施工质量、运行管理与维护等均密切相关，是复杂的系统工程，目前国内外对水电工程寿命的综合研究仍较少，综合考虑材料和结构、工程功能和经济社会层次因素的研究成果则更为鲜见。根据水利行业颁布的SL 654—2014《水利水电工程合理使用年限及耐久性设计规范》，对大坝水库等根据工程等级规定了设计使用年限，但该年限仅是参考相关建筑物行业给出，并不能完全适合水电工程特点和复杂性。

关于大坝退役准则，目前美国关于水电站退役的相关准则主要有：美国土木工程学会(ASCE)能源部水力发电专业委员会《Guidelines for Retirement of Dams and Hydroelectric Facilities》(《大坝及水电设施退役指南》)；美国大坝协会(USSD)《Guidelines for Dam Decommissioning Projects》(《大坝退役工程导则》)；美国亨氏科学等：《Dam removal science and decision making》(《退役坝拆除的科学与决策》)，其提出了水库大坝退役决策的大致步骤。国际大坝委员会(ICOLD)2018年提出《Dam Decommissioning-Guidelines》(《大坝退役导则》)，为大坝退役决策过程、监管批准程序、设计和施工要点、泥沙管理和运行监控提供指导。2011年，加拿大安达略省自然资源部在《大坝退役和拆除技术公告》中详细指出，大坝退役需考虑的因素和大坝退役决策框架等，为大坝退役提供了依据。国内水利工程退役相关规范包括SL 605—2013《水库降等与报废标准》和SL/T 791—2019《水库降等与报废评估导则》，其中前者主要规定了需要降等和报废的工程范围(主要聚焦大坝和水库本身安全问题)，后者主要规定了评估内容和程序(包括大坝和水库，以及经济社会影响和环境影响评估等方面)。

随着全球气候变化的影响，极端气候发生概率也越来越大，极端暴雨、洪水、地质灾害等对按照现有规范设计的大坝、泄水等建筑物等提出了严峻挑战。同时，随着社会经济发展和生活水平的提高，人类对可接受的风险也越来越低，对水工建筑物的安全性、可靠性也提出了越来越高的要求，如何准确评估已建大坝寿命是亟需研究的重大课题。

本文针对混凝土坝的寿命评估，从风险效益平衡的角度提出大坝寿命评估的准则，在此基础上构建了混凝土坝寿命评估的理论框架，并在简化条件下提出评估混凝土坝寿命的概化数学模型，可以对实际工程进行大坝寿命估算。

1 混凝土坝寿命评估准则

本文从风险和效益综合考虑来判定大坝是否应该退役。若大坝的年效益减去年维护成本加上拆除费用减去其存在带来的年失事风险不再大于零，则大坝应当拆除，寿命终止。即

B(t)-Cm(t)+Cd(t)-R(t)=0

(1)

式中，B为年效益；Cm为年维护成本；Cd为拆除费用；R为年失事风险值，它们均为时间的函数。其中，年失事风险值R取决于一年内大坝失事后果及其相应的失事概率，可定义为

R=C·P

(2)

式中，C为大坝失事后果；P为大坝失事的概率。

2 混凝土坝失事概率计算

随着服役时间增长，大坝混凝土老化会使得承载能力降低，本文主要考虑遭遇一定频率的洪水或地震导致混凝土坝失事的工况。混凝土的力学性质参数随时间的变化函数设为

M=M(t，A)

(3)

式中，M为混凝土的力学性质参数向量；t为时间；A为混凝土力学性质时变规律参数向量。

经有限元计算，可得在洪水作用下大坝达到极限状态对应的洪水水位

H=H(M)

(4)

由水文资料可得对应的洪水频率

PH=PH(H)

(5)

经有限元计算，可得在地震作用下大坝(常态运行水位下)达到极限状态对应的地震强度

INT=INT(M)

(6)

由地震资料可得对应的地震频率

PINT=PINT(INT)

(7)

则洪水或地震作用下大坝失事概率为

P=PH+PINT

(8)

3 混凝土坝失事后果和年效益计算

大坝失事后果原则上应进行溃坝分析后得到，年效益原则上应进行综合分析评估。为简便起见，本文按照与参考文献[6]类似的方法提出简化计算模型。

模型所需要的物理量包括：所在地GDP、所在地人口、最大坝高、库容、调节库容、坝型风险指数、多年平均发电量、上网电价等。其中，水电站所在地建议选取所在的县级地区，若处于两地区或多地区交界，则取平均值；坝型风险指数反映不同坝型对电站失事风险的影响，风险越大取值越大，建议重力坝取0.5，拱坝、闸坝取1，面板坝取1.5，心墙坝取2。

模型所需要的参数包括：人口因子、坝高库容后果因子、调节库容后果因子、衰减因子、附加洪水底数、附加洪水系数、调蓄效益系数等。各参数的用法及建议值将在下文模型介绍中给出。

记模型所需的物理量矩阵为X={xi，j}，其中，i为电站序数；j为物理量类别序数。模型所需的参数向量为A={ak}，其中，ak为模型参数；k为参数类别序数。为了计算大坝失事后果C，首先考虑第个电站溃坝产生的溃坝洪水在电站所在地的影响与最大坝高和库容有关，即

fi，i=a2xi，3xi，4

(9)

ci，i=(xi，1+a1xi，2)fi，i

(10)

溃坝洪水除对当地产生影响外，将向下游传递。在洪水传递到第l个电站时(i+1≤l≤m，m为电站总数)，传递到坝前的洪水影响相对从第l-1个电站下泄的洪水影响会衰减，设为

(11)

出于简化起见，本文对洪水的衰减仅考虑经过水电站的数目，即水电站的滞洪作用，不考虑洪水行进的路径等。

洪水从在第l个电站坝前到从第l个电站下泄，受到第l个电站两方面的影响。一是，第l个电站水库的调蓄作用，考虑该调蓄作用与第l个电站水库调节库容的大小有关，故设经第l个电站水库调蓄后洪水影响变为

(12)

另一方面，第l个电站在上游洪水的作用下可能产生附加洪水(如在上游洪水作用下溃决)，考虑该附加洪水与第l个电站的最大坝高、库容、坝型，以及上游洪水与第l个电站库容的比值有关，设为

(13)

另外，若调蓄后洪水影响为0，则下泄洪水影响亦为0。从第l个电站下泄的洪水影响为

(14)

则洪水对第l个电站所在地产生的后果为

ci，l=(xi，1+a1xi，2)fi，l

(15)

如此可以递推计算第i个电站溃坝洪水对下游各梯级所在地产生的后果。若fi，l=0，则溃坝洪水对其下游梯级皆无影响，即ci，k=0(l+1≤k≤m)，则第i个电站的溃坝洪水对流域产生的后果为

(16)

随着教育的改革，小学英语的教学也应该得到更新，翻转课堂的教学模式在英语教学中能够使师生之间取长补短，互相学习，改善师生之间的关系，可以最大程度提高课堂学习效率和学生学习英语的热情。

(17)

(18)

水电站效益Bi为

(19)

对任意一个大坝，根据其在流域中的位置由式(9)～(19)计算得到的Ci+Bi(失事后效益不再存在，亦应计入大坝失事后果中)，作为式(2)中的大坝失事后果C；计算得到的Bi作为式(1)中的年效益B。需要说明的是，本文暂不考虑大坝失事后果和年效益随时间的变化。

4 混凝土坝寿命计算

为简化起见，暂不考虑年维护成本和拆除费用随时间的变化，则Cm和Cd仅为两个常数函数。则由式(1)～(19)结合有限元计算可以解出t=T为大坝寿命。后续可以通过考虑年效益(调整运行水位)等的变化，研究如何采取降水位运行等措施来延长大坝寿命。为验证模型可行性，将式(3)～(7)通过材料试验研究、有限元计算得到的函数假定出来，便于编程序计算。

中国电建集团成都勘测设计研究院有限公司对混凝土材料抗压强度、抗劈拉强度随冻融循环的变化关系进行了研究[1]，成果如图1所示。从图1可以看出，其规律基本为指数型。则式(3)可假定为

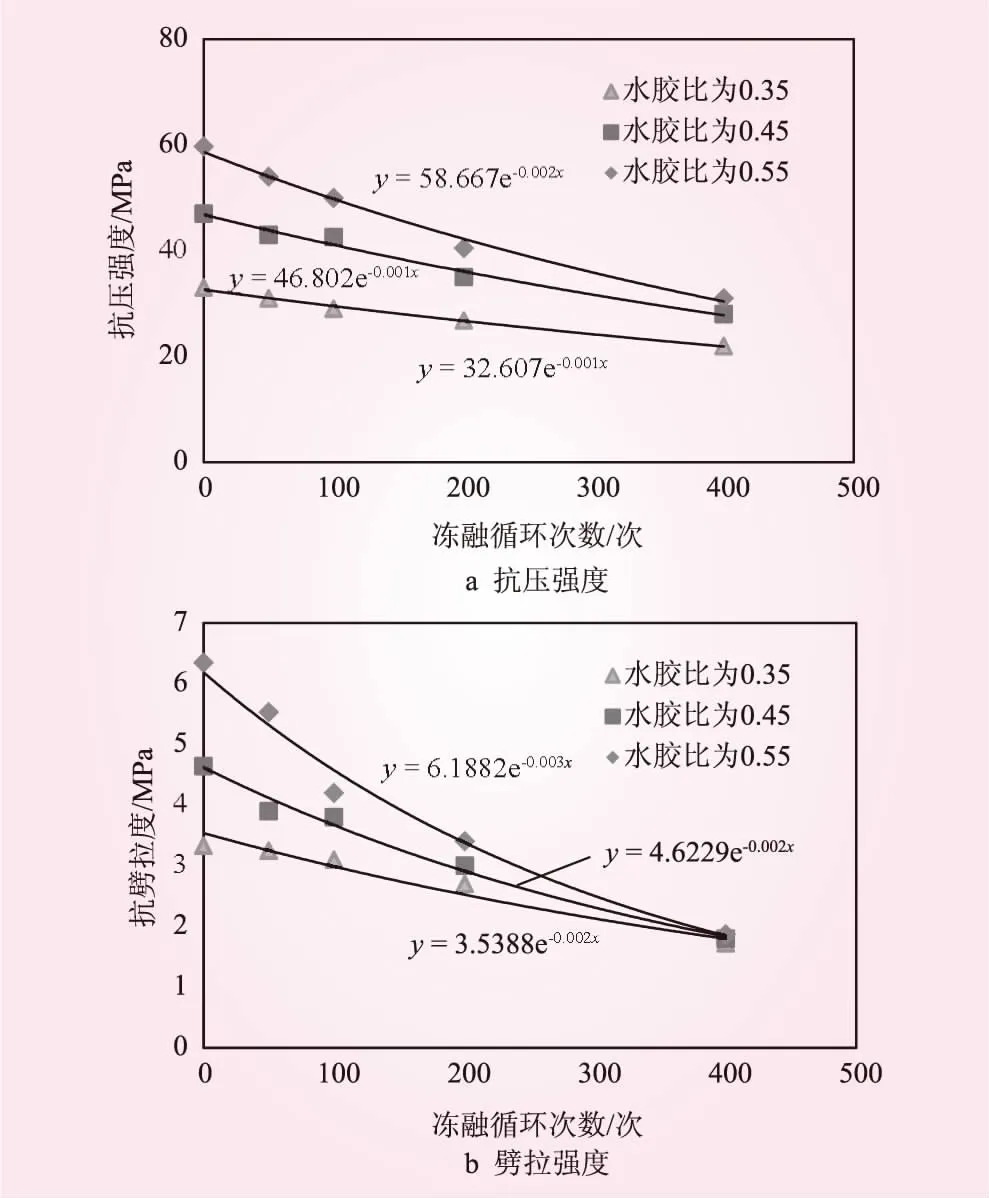
图1 混凝土材料抗压强度、抗劈拉强度随冻融循环的变化关系

M=M0eb1t

(20)

式中，M0为混凝土材料初始强度；b1为混凝土材料

强度时变指数；t为时间。

一般而言，大坝承受的载荷和材料强度、模量等性质正相关。式(4)、(6)假定为

(21)

(22)

洪水频率曲线一般采用P-Ⅲ曲线、logP-Ⅲ曲线等，为简化程序，假定为指数型，地震强度也假定为指数型，则式(5)、(7)假定为

(23)

(24)

式中，下标为0的值代表建成时的值。到此便可以编程序计算。模型参数的建议值见表1。

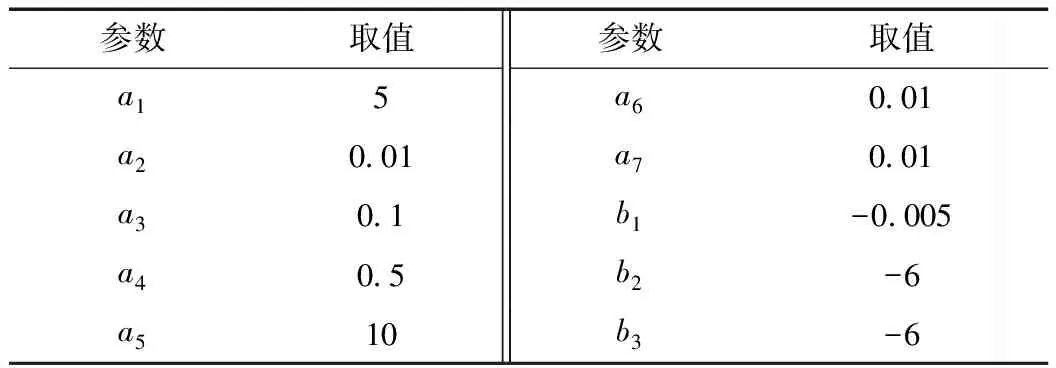
表1 模型参数建议值

5 实例分析

依据本文提出的模型，对大渡河流域已投产的14座梯级水电站进行风险效益综合规划分析，14座水电站详细信息见表2。

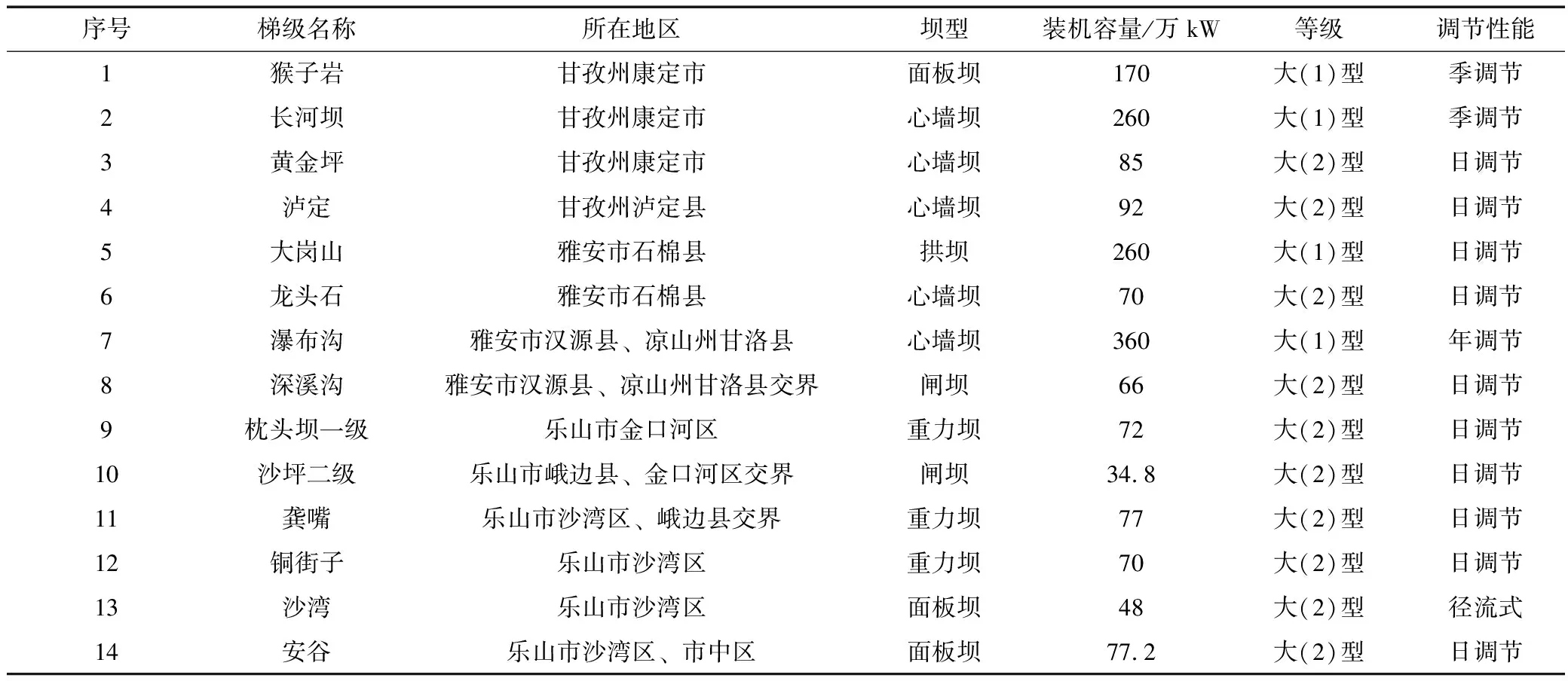
表2 大渡河已投产梯级水电站信息

模型所需物理量取值见表3。其中，所在地GDP和所在地人口按2015年的统计值；龚嘴和铜街子的动态投资参照枕头坝一级按其装机成比例换算而来；上网电价统一取0.3元/(kW·h)。模型参数按表1取值。

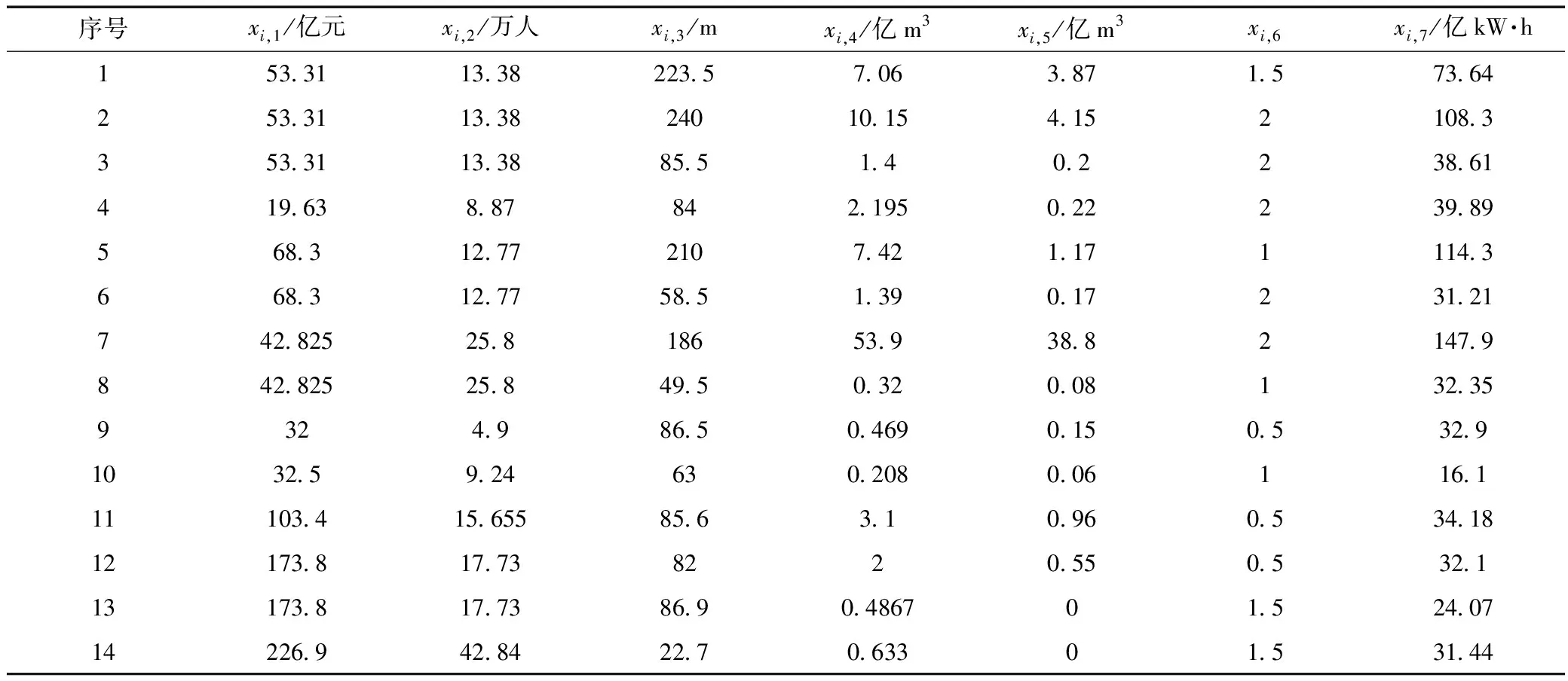
表3 大渡河已投产梯级水电站模型参数

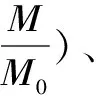
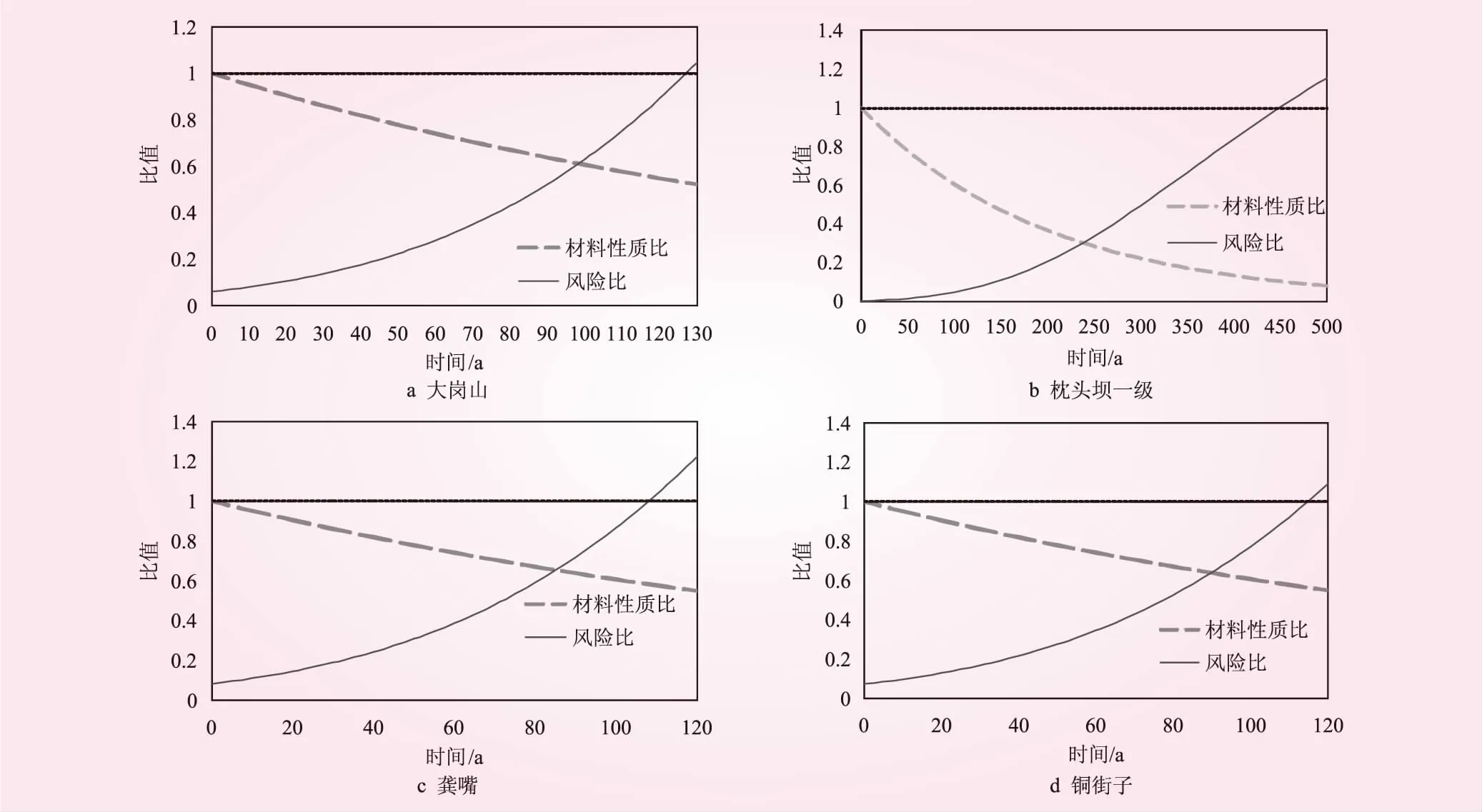
图2 大坝材料性质比、风险比计算结果

6 结 语

本文针对混凝土坝因坝身材料老化会导致承载力降低的特点，考虑其失事风险随使用年限的增加逐渐增大，提出了风险效益平衡作为大坝使用寿命的评估准则。通过计算大坝在洪水和地震作用下的失事概率和失事后果，确定大坝失事风险，基于风险效益平衡准则确定大坝寿命。在这个理论框架的基础上，通过简化假设，提出了可以估算实际工程大坝寿命的概化数学模型，并对大渡河上大岗山、枕头坝一级、龚嘴、铜街子4座混凝土坝的寿命进行了估算，验证了模型的可行性。