并联谐振感应加热电源电路的设计与研究
阮景奎,周玉宁,何正龙
1.湖北汽车工业学院 湖北十堰 442002
2.十堰高周波科工贸有限公司 湖北十堰 442013
1 序言
感应加热技术具有节能、加热效率高、可控性强等优点,是先进的热处理技术,在金属工业领域得到广泛应用[1]。
杨玉岗等[2]提出一种LCLC谐振变换器,在变压器的一次侧并联一个LC支路,有效保证LLC型谐振高效率的同时,实现谐振变换器的对称双向运行;余功成等[3]提出了采用IGBT和逆变桥双重并联的扩容方法,有效地提高了大功率并联谐振型感应加热电源的稳定性和功率密度;JONATHAN ZERAD等[4]根据感应加热负载非线性的特性,设计了非线性控制器用于频率跟踪。近年来的研究表明,改进电路结构,是提高感应加热电源效率和性能的主要途径。
风电轴承是一种特殊的零件,其自身半径大、使用工况条件恶劣,对于轴承本身需具有良好的密封性、润滑性、耐冲击和可靠性,而感应加热技术正是优化该类产品工艺、提高表面质量的关键所在。本文结合风电海装高精轴承感应热处理,进行45kW的并联谐振感应加热电源电路设计,研究了电源电路的关键技术,为感应加热技术的发展助力。
2 电源电路设计
2.1 电源结构
感应加热系统由整流、滤波、逆变、负载以及控制电路等构成。整流系统经滤波后产生直流电压,通过逆变控制电路控制,把直流电压再按一定频率转换为交流电压,提供给负载,整个过程形成了经典的 AC/DC/AC 变换形式[5]。感应加热电源的基本结构组成如图1所示。
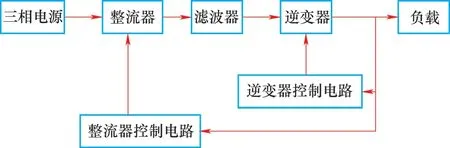
图1 感应加热电源的基本结构组成
2.2 谐振模型分析
感应加热电源谐振电路一般包括:串联谐振电路、并联谐振电路、串并联混合电路。相较于其他两种谐振电路,并联谐振电路可以空载运行,由于直流侧串联大电感,当发生过流或短路时,拓扑本身具有一定的保护能力,因此采用二阶RLC并联谐振电路作为研究对象。
并联谐振电路由电阻、电容、电感并联组成。谐振时,电压、电流同相位,电源只提供电阻所需要的有功功率。并联谐振等效电路如图2所示。
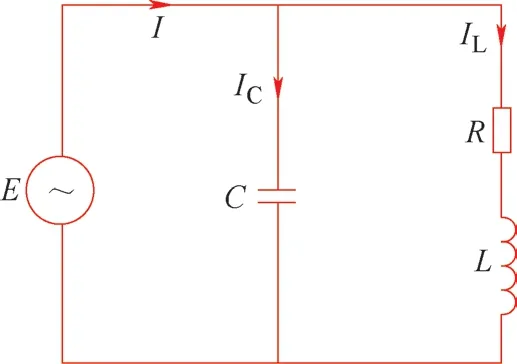
图2 并联谐振等效电路
假设交流电源E为理想电源,则负载总阻抗为
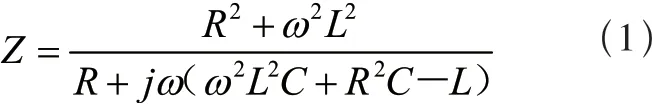
式中Z——负载总阻抗(Ω);
R——电阻(Ω);
L——电感(H);
C——电容(F)。
当谐振发生时,阻抗的虚部为0,即
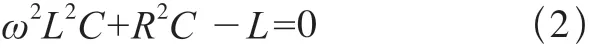
对于式(2),通常情况下等效电阻R很小,可忽略其对角频率ω0的影响,因此有

此时谐振电路总阻抗Z0为
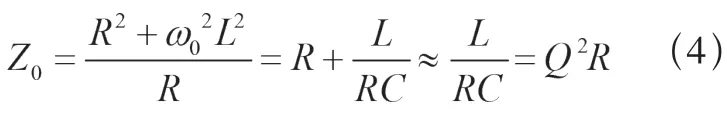
式中Q——品质因素。
总电流I0为
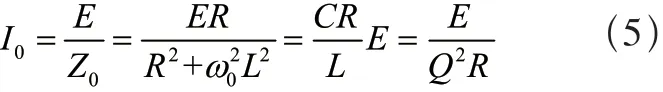
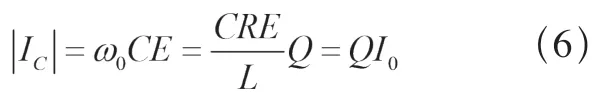
综上分析可得,谐振发生时,负载总阻抗很大,总电流却小于各支路电流,故并联谐振又称为电流谐振。对于总阻抗Z0,可通过电阻、电容、电感进行调节,这就使负载匹配更加灵活、适应性更强。
2.3 电路设计
对用于直径4m滚道热处理的感应加热电源,设计了一种基于并联谐振电路的仿真模型。主回路中采用三相晶闸管整流,输入电源为 380V/50Hz 交流电,主要包含三相全桥相控整流部分,直流输出滤波采用大功率电感滤波,逆变桥开关管采用4个IGBT器件构成全桥理想模型,以及RLC并联谐振电路和控制电路。感应加热系统电源电路结构如图3所示,其中线路上的方点为各元器件接点。
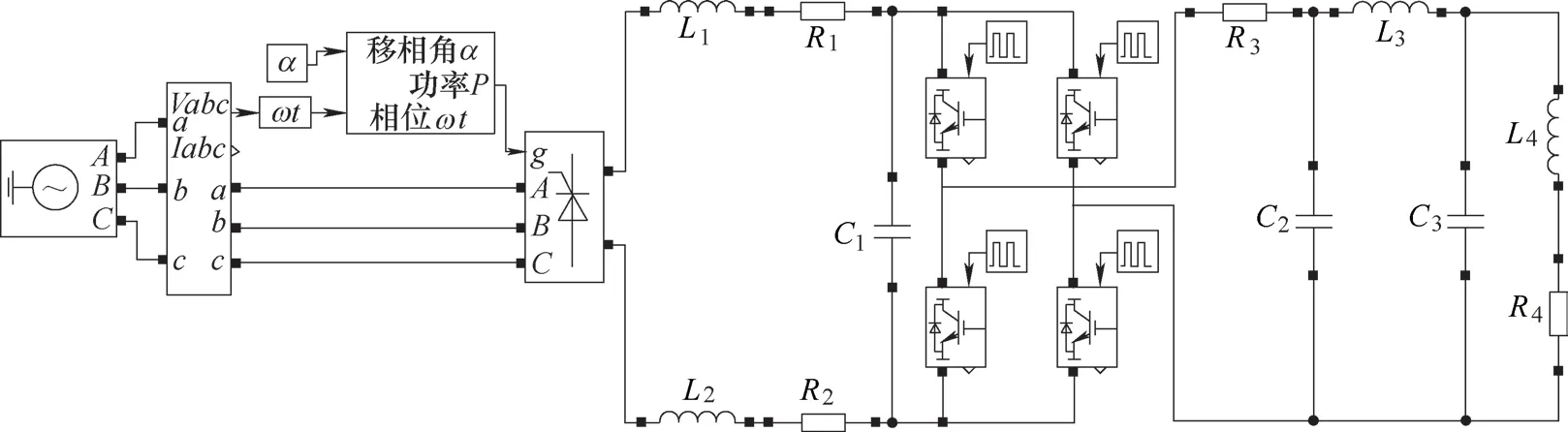
图3 感应加热系统电源电路结构
3 控制策略设计
3.1 神经网络PID控制
以传统增量式PID算法为基础,结合神经网络的快速自适应学习能力,设计一种神经网络PID算法,通过实际与给定条件间的误差反馈补偿,从而实现自整定控制。神经网络PID控制系统结构如图4所示。
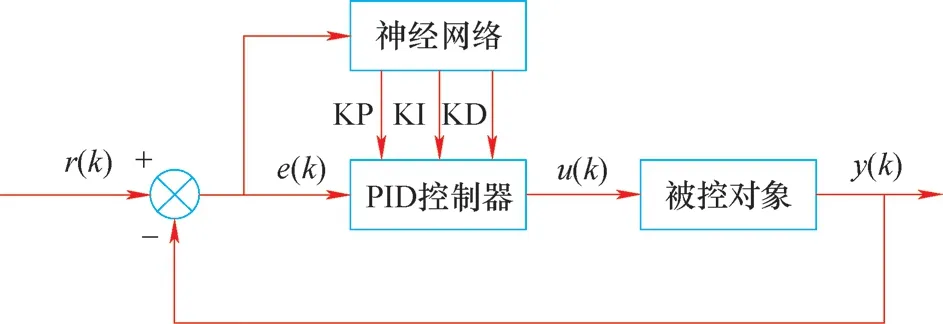
图4 神经网络PID控制系统结构
传统PID算法增量表达式为
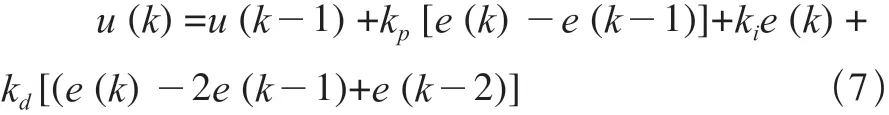
式中u(k) ——k时刻控制量;
e(k) ——k时刻反馈误差量;
kp——比例系数;
ki——积分系数;
kd——微分系数。
对于神经网络PID控制系统,将式(7)中的kp、ki、kd视为可变参数,并且与系统状态间呈非线性关系,此时利用神经网络算法进行训练和学习,快速找到系统控制规律,确定当前时刻kp、ki、kd最佳值,式(7)可描述为

离散化的控制器控制算法如下。
Step1:令k=1,即当前时刻为1,确定网络结构及参数。
Step2:计算k时刻采样误差e(k)=r(k)-y(k)。
Step3:计算各层神经元的输入、输出,确定kp、ki、kd。
Step4:计算确定参数kp、ki、kd下的PID控制器输出u(k)。
Step5:进行神经网络学习,实现kp、ki、kd自整定调节。
Step6:判断误差e(k)是否满足要求,若不满足k=k+1,则跳转至Step2进行下一轮循环;若满足,则停止迭代。
以同一被控对象G(s)=1/(20s+1) 为例,传统PID和神经网络PID控制系统阶跃响应曲线对比如图5所示。
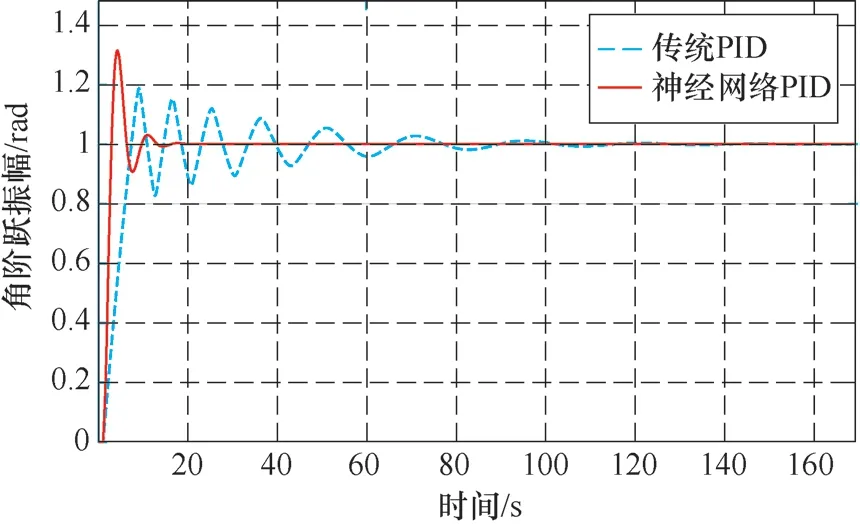
图5 传统PID和神经网络PID控制系统角阶跃响应曲线
由图5可以看出,使用神经网络PID控制器的系统出现误差时反应速度更快,有效减少了静态误差,且系统的稳态性能得到了改善。
3.2 功率调节
整流器采用三相全控整流方案,控制器采用神经网络PID功率反馈调节策略,三相全控整流方案原理如图6所示。由于整流器的输出电压脉动幅度较大,利用滤波器过滤掉交流成分,完成AC/DC转换,从而保证逆变器输入端为直流电。

图6 三相全控整流方案原理
三相桥式全控整流电路的输出电压为
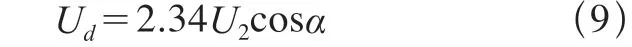
式中Ud——直流电压平均值(V);
U2——相电压有效值(V);
α——触发移相角(rad)。
当全控制晶闸管整流桥触发移相角α改变时,整流器输出的直流电压平均值是可以控制的,从而可以控制输出功率大小。通过采样电流和电压作为反馈信号,计算给定功率与实际功率误差,利用神经网络PID进行自整定调节,可以得到新的相控角α,进而保证稳定的输出功率[6]。
4 仿真与验证
按照图3感应加热系统电源电路原理图搭建MATLAB模型进行仿真验证,输入电压380V,输出功率45kW,其他电路元件参数见表1。
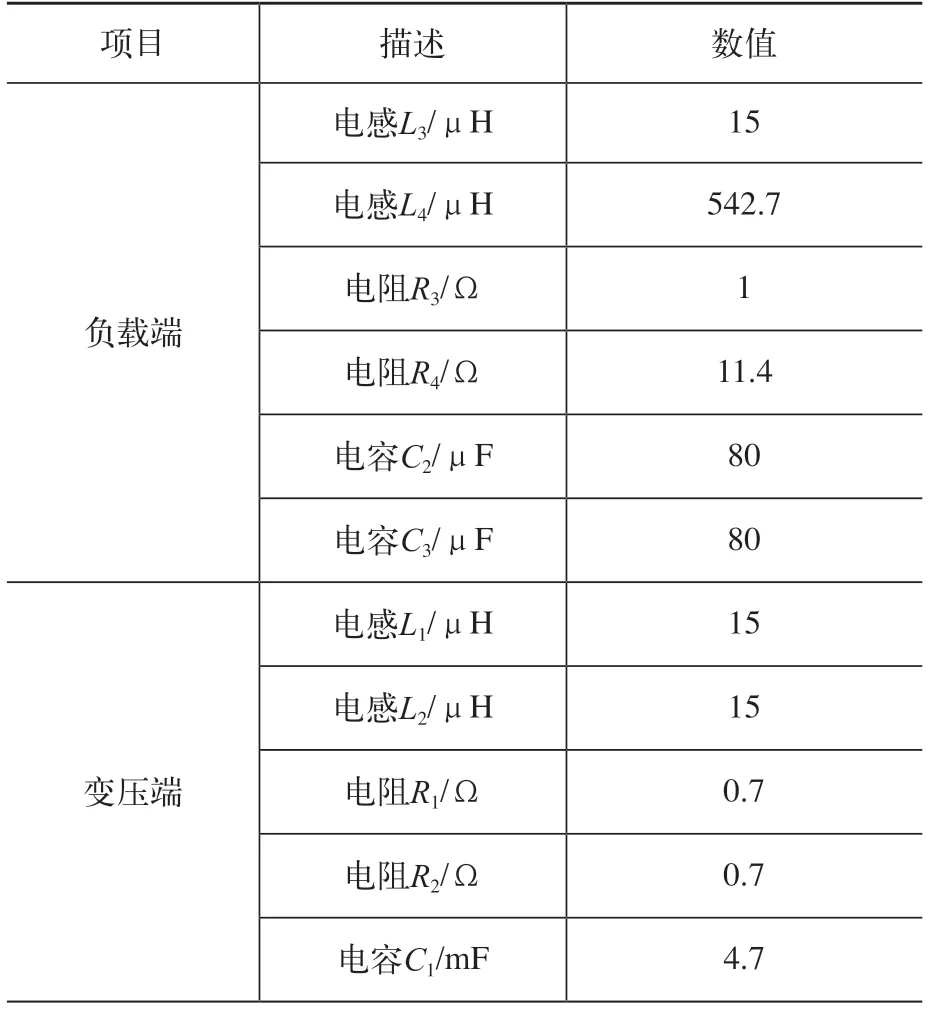
表1 感应加热系统电源电路参数
经试验得到负载端电流、电压、输出功率波形,如图7~图9所示。
由图7、图8可知,负载电压为正弦波、电流为方波,直流侧相当于电流源,符合并联谐振电路特点,且无杂波,输出电压、电流稳定。

图7 负载电流波形
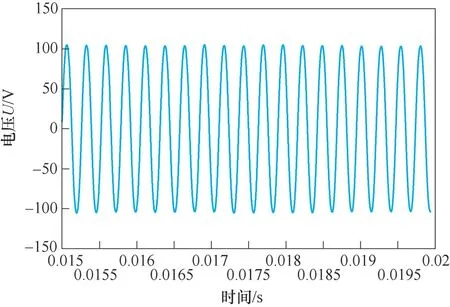
图8 负载电压波形
由图9可知,感应电源输出功率稳定在45kW,符合最初设计要求。
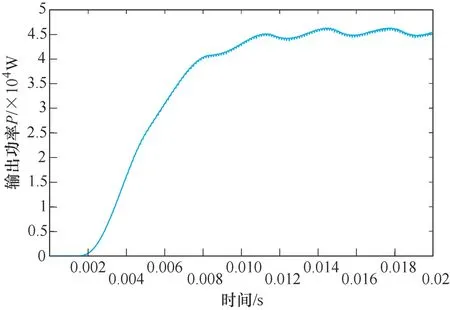
图9 输出功率波形
5 结束语
为实现设备工作高效运行,降低无功损耗,对并联谐振感应加热电源结构及电路进行了理论分析。通过电压、电流采样,使用神经网络PID算法,将给定功率与实际功率进行比对,实现闭环反馈。通过调节移相角α,改变直流侧电压值,从而达到功率调节的目的。最后利用MATLAB SimuLation进行仿真验证,结果表明感应加热电源电路输出电压、电流及功率稳定,符合最初设计要求。

