考虑禁止区间约束的水火电力系统短期调度优化

王光政，孟 盼，刘良雨

(华北水利水电大学电力学院，河南 郑州 450000)

0 引言

随着化石能源的不断减少，可再生能源装机容量的不断上升，以及在“碳达峰”和“碳中和”的大背景下，电力调度由传统火电机组运行转向火电与可再生能源联合运行调度。其中水火联合调度优化，一直是经典的研究课题之一。其目的是，在满足各种条件约束的情况下，合理安排火电机组出力以及水电站出力，使得总的火电机组燃料费用最小。如何使所建立的模型更加精确符合实际情况以及寻找更加高效实用的求解算法，一直是学者们主要的研究方向。从数学的角度看，水火联合调度模型具有非线性，非凸性，耦合性强以及维数多的特点。传统的数学方法，在面对大规模问题时，由于会陷入维数灾而无法找到最优解[1]。群体智能优化算法是近几十年来兴起的一种求解复杂问题的方法，其不受目标函数的形式以及复杂约束的限制。近年来，相继被运用于求解水火联合调度问题，并取得了不错的效果[2- 6]。

由于发电机物理结构特性等原因，机组在某些区间运行，会发生不稳定的情况，称之为禁止出力区间[7- 8]。在调度时需要避免发电机运行在该出力区间段。为了使模型更加符合实际情况，降低电力系统运行的风险。因此，本文从模型的角度出发，将禁止区间约束条件加入到水火联合调度模型中。

麻雀搜索算法(SSA)是薛建凯等人于2020年提出的一种新型群体智能优化算法[9]，该算法基于麻雀种群中的觅食行为和反捕食行为，与其他智能算法相比，具有求解速度快，稳定性和收敛精度高的特点。一经提出便受到了学者的广泛关注[10]。本文将SSA算法应用于水火电力系统调度优化，并取得了不错的实验效果。

1 水火电力系统优化调度模型

1.1 目标函数的构建

以火电机组的燃料费用Fc最小为目标函数

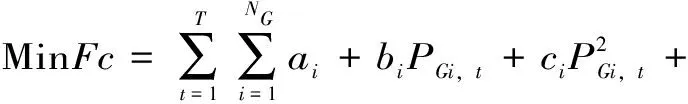
(1)

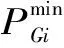
1.2 火电约束条件的建立

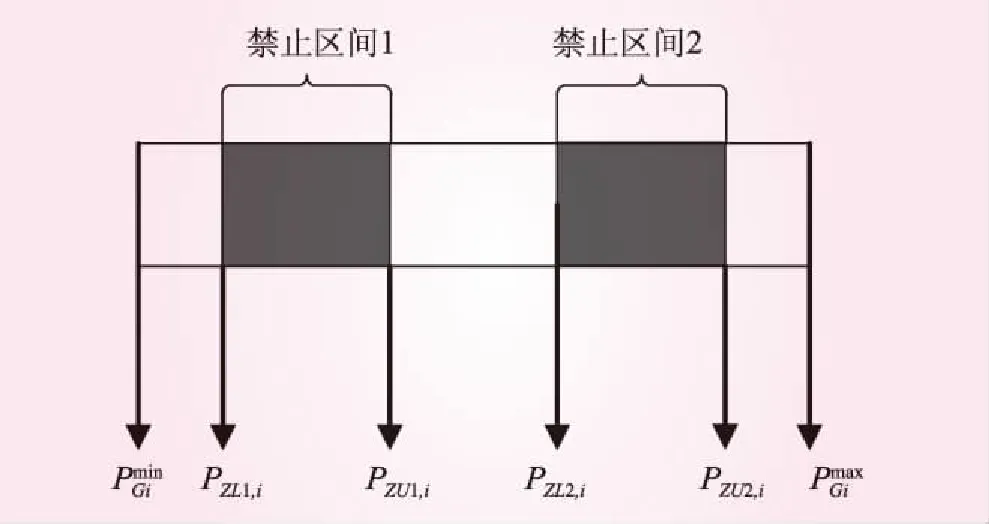
图1 禁止区间示意

(2)

逻辑约束条件模型为

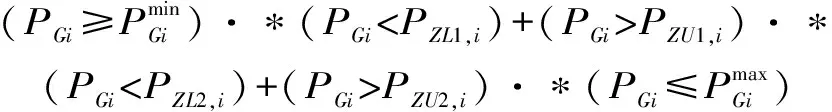
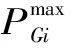
(2)功率平衡条件约束

(3)

式中，Nh为水电厂的个数；PGi，t为第i台火电机组在t时段的出力；Phj，t为第j个水电站在t时段的出力；Pload，t为t时段的负荷值。

(3)火电机组出力上下限约束

(4)

(4)火电机组爬坡、滑坡约束

(5)

式中，PGi，t-1为第i台火电机组在t-1时段的出力；PGi，t+1为第i台火电机组在t+1时段的出力；URi为第i台火电机组的爬坡速率限制；DRi为第i台火电机组的滑坡速率限制。

1.3 水电约束条件的建立

(1)水电厂出力上下限约束

(6)

(2)水库库容约束

(7)

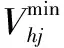
(3)发电引用水流量约束

(8)

(4)水量平衡约束

(9)

式中，Vhj，t+1为第j个水电厂在t+1时段的库容；Ihj，t为第j个水电厂在t时段的来水量；Shj，t为第j个水电厂在t时段的弃水量；Nw为位于第个j水库的上游水库的总数；τkj为第k个水库到第j个水库的水流延迟时间。

(5) 水电出力转换约束

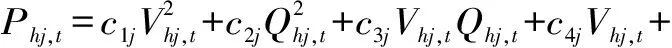
(10)

式中，c1j、c2j、c3j、c4j、c5j、c6j为水电厂j的拟合系数。

2 麻雀搜索算法

在SSA算法[9]中，每只麻雀代表一个可行解，麻雀分为发现者和加入者，发现者通常拥有较高的能源储备(也就是所对应的适应度值)，发现者和加入者可以相互转换，但是总比重是不变的。当麻雀意识到危险时，会迅速向安全区移动，以获得更好的位置。

2.1 发现者位置更新模型

在SSA中，发现者负责为整个麻雀种群寻找食物，并为加入者提供觅食的方向，发现者可以获得比加入者更大的搜索范围。在每一次的迭代过程中，发现者的位置更新如下所示

(11)

式中，t为当前迭代次数；j=1，2，3，…，d；itermax为最大迭代次数；Xi，j为第i只麻雀在第j维中的位置；a∈(0，1]是一个随机数；R2(R2∈[0，1])和ST(ST∈[0.5，1])分别表示预警值和安全值；Q为服从正态分布的随机数；L为一个1×d的矩阵，矩阵中的每个元素均为1。

2.2 加入者位置更新模型

在觅食过程中，一些加入者会时刻监视着发现者。它们一旦察觉发现者找到了更好的食物，会去争夺食物。加入者的位置更新如下所示

(12)

式中，Xp为目前发现者的最好位置；Xworst为当前全局最差的位置；A为一个1×d的矩阵，其中每个元素为1或-1，且A+=AT(AAT)-1。

2.3 意识到危险的麻雀位置更新模型

假设这些意识到危险的麻雀占总数量的10%～20%。且其初始位置是随机产生的，其位置更新为

(13)

式中，Xbest是当前全局最优位置；β作为步长控制参数，是服从均值为0，方差为1的正态分布随机数；K∈[-1，1]是一个随机数；fi为当前麻雀个体的适应度值；fg和fw分别是当前全局最好和最差的适应度值；ε是值很小的常数，以避免分母出现0。

3 基于SSA算法的优化调度流程

SSA算法流程如图2所示。

图2 SSA算法流程

(1)如图2所示，输入SSA算法相关参数，建立水火联合调度电力系统模型并设置好相关参数。

(2)初始化麻雀的位置，设置变量的上下限范围。在目标模型中以火电机组出力以及水电站发电引用水流量作为优化控制变量，以火电机组燃料费用最小为目标函数，同时相关约束条件以惩罚函数的形式加入到目标函数中。

(3)计算每个麻雀的适应度函数值，确定最优值和最差值及其相应位置。

(4)根据式(11)～(13)更新发现者，加入者和意识到危险的麻雀的位置。

(5)获得当前最优值，如果当前最优值比上一次迭代的最优值好，则进行更新操作，更新全局最优位置和最佳适应度值。

(6)重复步骤(3)～(5)，直到满足最大迭代次数为止，最后输出最优结果。

4 案例仿真计算

本文采用一个含有6台火电机组和有4个水电站的梯级水电站群的测试系统进行仿真计算。水电站的相关参数来自文献[2]，各个火电机组相关参数来自文献[11]。为了验证SSA算法的有效性，本文还与GWO算法和PSO算法进行了对比分析。设定种群规模均为300，最大迭代次数均为150，调度周期均为24 h。SSA算法求解出的最优调度方案如表1所示，图3给出3种算法的对比收敛曲线，图4给出了24 h的负荷需求情况。

表1 采用SSA算法的水火电力系统优化调度结果

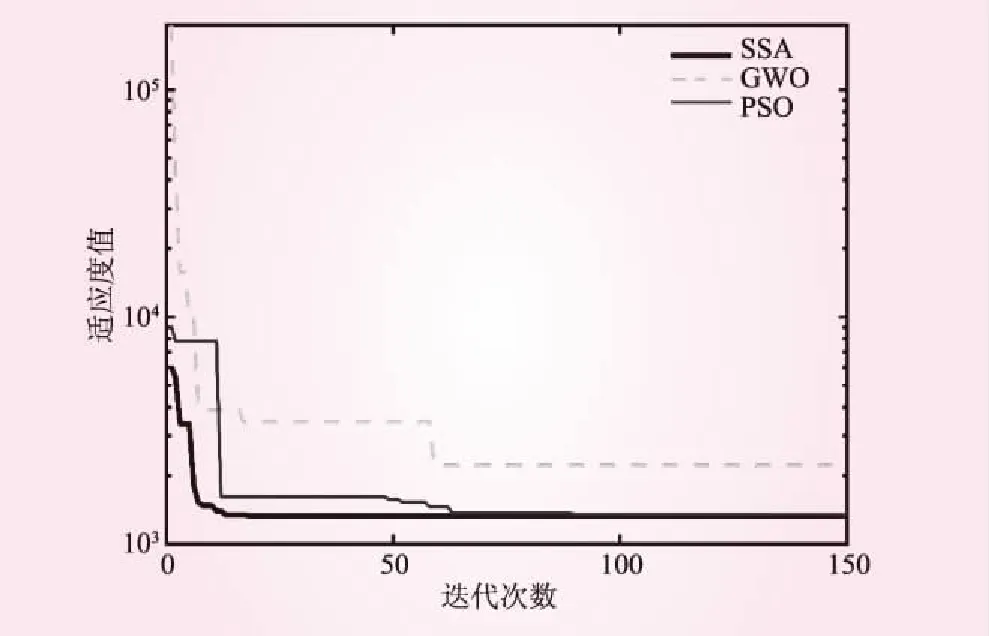
图3 3种算法的收敛曲线

图4 系统负荷值

从图3可以看出，SSA算法相较于GWO算法，在求解本问题时，寻优能力更强。同时SSA算法对比PSO算法可以看出，SSA算法在15代左右下降很快，在达到30代时，结果趋于平稳，收敛速度快，稳定性好，表明算法得到了最优解。

图5、6分别给出了24 h的水电机组发电引用水流量情况以及水电和火电机组的出力分配情况。结合文献可以看出，在调度周期内，水电4和火电1相较于其他机组出力值较大。水电以及火电机组的出力是满足上述等各种约束条件的。经过验算，验证了调度方案的合理性。

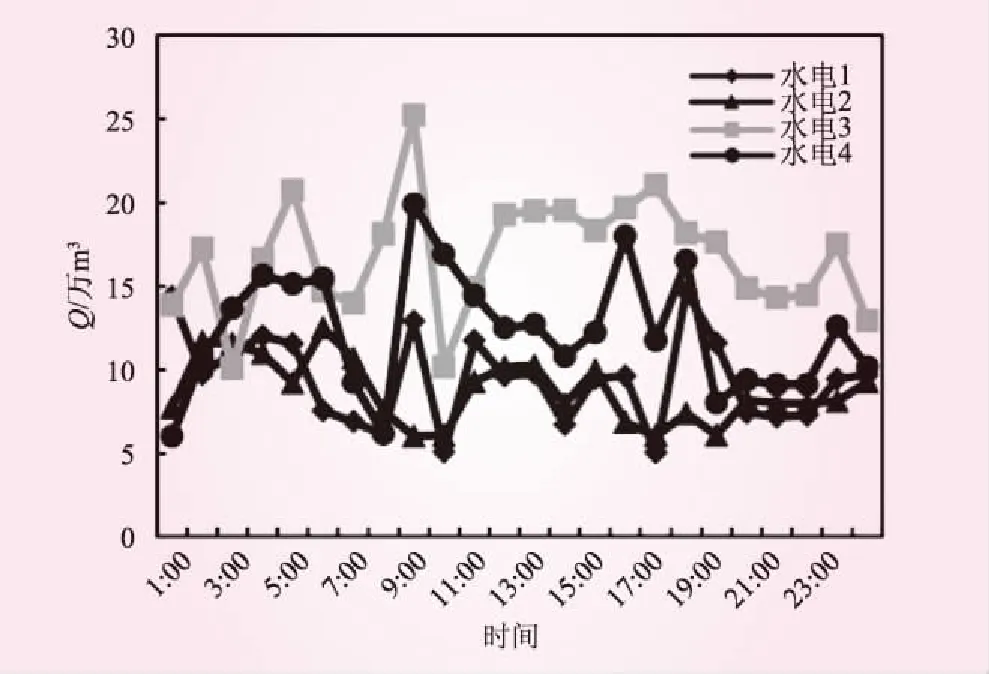
图5 发电引用水流量

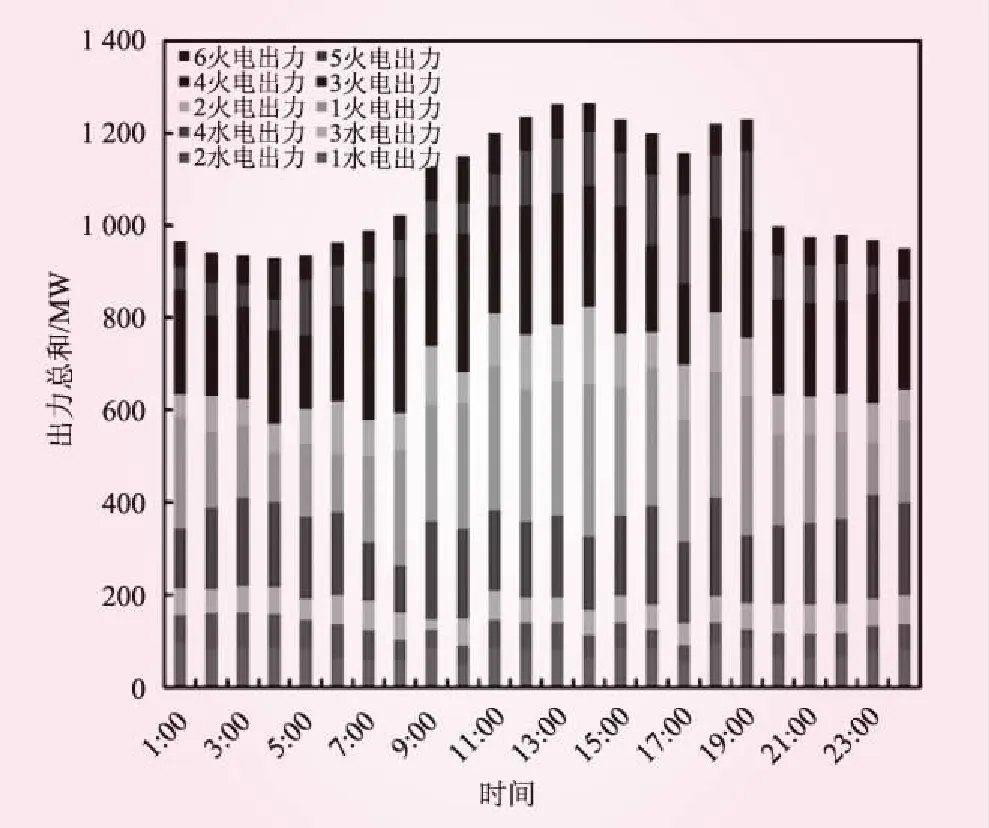
图6 水火出力分配示意

图7给出了SSA算法所求得的最优24 h时刻的费用曲线。结合参考文献[11]的发电机组产生的费用数据，验证了所得费用曲线的合理性。从费用曲线中不难看出，机组产生的费用随着负荷的变化，也是在不断变化的。

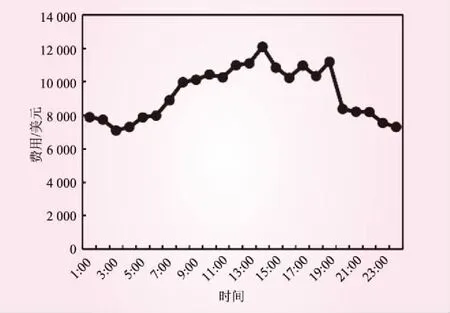
图7 费用曲线示意

5 结 语

针对火电机组物理组件的限制，发电机在某些运行区间内出力，不利于机组安全运行的特点。本文将火电机组禁止运行区间约束条件，加入到水火联合调度优化模型中。使得模型更加完善精确，符合实际运行情况。约束条件采用逻辑运算的方式生成，同时适当设置权重，采用惩罚项的形式加入到目标函数中。采用SSA算法对模型进行求解，在MATLAB中进行仿真计算，并与PSO和GWO算法进行对比。实验结果表明所提模型的合理性和SSA算法的有效性。