巷道掘进药卷与钻孔直径匹配关系对爆破破裂范围的影响*

王姚姚，汪海波，程 兵，宗 琦，谢 平，王梦想

(1.安徽理工大学 土木建筑学院，淮南 232001；2.淮南矿业(集团)有限责任公司 顾北煤矿，淮南 232001)

不耦合装药结构因其空气间隔的存在，可以降低岩体爆炸冲击波的作用强度、延长爆生气体作用时间，主要用于光面爆破和预裂爆破等[1-4]；耦合装药结构可更好地利用炸药爆炸应力波进行破岩，用于深孔爆破增透和硬岩巷道掘进等方面[5-6]。程兵通过LS-DYNA模拟软件分析不同耦合系数炮孔周边裂纹分布状况[7]，推断出不耦合侧岩体中应力峰值不仅小于耦合侧，且出现的时间也滞后于耦合侧；宗琦推导出了冲击波作用的压坏区和裂隙区扩展半径公式[8]；戴俊利用Mises强度准则并考虑岩石三向受力及其强度的应变率效应[9]，推导出柱状药包爆炸在岩石中引起的压碎圈与裂隙圈半径的计算式。龚敏对松软煤层深孔爆破的力学性能进行了研究[10]。

在煤矿巷道掘进实际工程中，钻孔直径主要有32 mm、35 mm、42 mm，炸药药卷直径有27 mm、29 mm、32 mm、35 mm。具体采用哪种组合，取决于现场施工人员习惯。基于现有研究成果，利用ANSYS/LS-DYNA有限元软件建立爆破计算模型，得到不同孔径和药卷直径组合时模型体内的有效应力，分析了不同组合工况爆破应力波传播过程和爆破效果的影响，为岩巷硬岩爆破掘进提供理论依据。

1 耦合装药破岩理论计算

1.1 岩石损伤准则

爆轰冲击波的强压缩导致粉碎区的形成，消耗了部分的能量，使冲击波迅速衰减成应力波向岩体四周传播，进而形成裂隙区。此情况可以简化为平面应变问题，则岩石中任意一点所受到的应力可以表示为[11]

(1)

岩体的损伤准则主要由岩体的性质和其实际受力条件决定，在爆破荷载中，炮孔周边岩体受到压缩、剪切和拉伸三向应力状态，因此岩体中任意一点的受力状态为[8]

(2)

将式(1)代入，得

(3)

根据岩石损伤准则和Mises准则，岩石的损伤可以表示为：在压碎区σi=σcd；在裂隙区σi=σtd。其中，σcd和σtd分别为岩石的动态抗压强度和动态抗拉强度。

相比较静态荷载，岩石材料对爆炸产生的荷载更加敏感。一般情况下，岩体的动态抗拉强度是随着应变速率得增大而增大，根据已有研究，由于不同得岩石材料对应变速率得敏感度不同，因此对于常见的岩石材料，可以近似表示岩石的动态抗拉强度和抗压强度为[12]

(4)

1.2 岩石粉碎区和裂隙区的计算

爆炸裂隙区半径计算常用的公式为[14]

(5)

式中：rt为裂隙区半径；rb为炮孔半径；Pr为炮孔壁初始压力；St为岩石的抗拉强度。

其中，炮孔壁初始压力

(6)

式中：ρ0为炸药密度；D为炸药爆速；dc为炸药半径；λ为测压系数，取λ=8。

文献[15]研究研究表明，炸药的爆速与药卷直径有关，研究的结果见表1。

表 1 不同直径炸药的爆速[15]

为保证粉碎区和裂隙区数据的合理有效，计算以某巷道掘进为背景，该巷道岩石的物理力学性能测试结果平均值为：抗压强度92.15 MPa，抗压强度4.90 MPa，弹性模量68.14 GPa，泊松比0.234。

2 计算模型与参数

现场爆破作业主要采用柱状装药，且炮孔直径远远小于其炮孔长度，所以在不考虑炸药端部的影响，将其做单层网格进行模拟[16]。研究使用ANSYS/LS-DYNA动力有限元软件建立尺寸为150 cm×150 cm×0.25 cm的1/4爆破模型，其中：炮孔直径为32 mm时，炸药直径分别为27 mm、29 mm和32 mm；炮孔直径为35 mm时，炸药直径分别为27 mm、29 mm和35 mm；炮孔直径为42 mm时，炸药直径分别为27 mm、29 mm、35 mm和42 mm。各个模型的起爆点设置在同一点，通过*INITIAL_DETONATION关键字定义位置。模型主要由炸药、岩石和空气三部分组成，其中岩石采用LAGRANGE网格建模；炸药和空气采用Euler网格建模，单元使用ALE算法，并且利用关键字*CONSTRAINED_LAGRANGE_IN_SOLID函数实现将炸药、岩石和空气之间的耦合。

炸药采用*MAT_HIGH_EXPLOSIVE_BURN材料模型来模拟爆破过程，爆轰产物的体积、压力和能量特性通过JWL状态方程进行描述[17，18]

(7)

式中：p为方程确定的爆轰压力；A、B为炸药常数；w表示压力与内能的变化比，及格林爱森参数；R1、R2为无量纲常数；V为爆轰产物的相对体积；E0为爆轰的初始内能。炸药的材料参数见表2。

表 2 炸药材料参数

空气采用LS-DYNA中的材料模型*MAT_NuLL，其状态方程采用*EOS_LINEAR_POLYNOMIAL定义，表达式为[19]

p=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)E

(8)

式中：p为爆轰压力；C0～C6为常数；V是相对体积；E为单位体积的内能。材料参数见表3。

表 3 空气材料参数

考虑到岩石为脆性材料、具有各向异性性质的弹塑性体。采用*MAT_PLASTIC_KINEMATIC作为岩石材料弹塑性模型。岩石材料模型参数采用前述测试结果。

3 模拟结果及其数据分析

3.1 岩体中应力波的传播

将LS-DYNA Solver求解出来的结果，利用后处理软件LS-Prepost中的映射功能将1/4模型映射成整体模型，更加有助于观察单孔爆破有效应力波在岩体内的传播和衰减。得到典型时刻有效应力云图如图1所示。

由图1，炸药爆炸后应力波在岩体内迅速向四周扩散，造成岩体破碎。伴随冲击波向裂隙区的传播，应力波峰值压缩的岩体会向应力波传播的反向产生拉应力，进而岩体受拉产生裂隙。

3.2 不同耦合系数有效应力波分析

选取距炮孔中心10 cm、20 cm、35 cm、50 cm、70 cm、90 cm的单元，记为A～F，分析不同条件下岩体内的有效应力波分布规律。通过LS-PREPOST后处理测出其相关数据，可以得到各点应力随时间变化曲线图，并且可以很直观看出各点受到的峰值应力，以及衰减变化历程，如图2所示(图2中各分图标题中k为不耦合系数)。

图 1 42 mm单孔耦合装药不同时刻有效应力云图

通过图2可以看出，在爆炸初期岩石受到炸药的爆轰作用，岩石受到的有效应力急剧增加达到峰值。随着炸药爆轰过程的进行，炸药释放的能量不断被消耗，岩石受到的有效应力不断减小。从图中可以看出炸药起爆后，距离炮孔中心最近的单元A、B其受到的有效应力急剧上升并率先达到峰值，较远的单元E、F随后相继达到峰值并且增长速度相较于A、B单元缓慢，应力波动幅度亦小于A、B单元，很明显炸药爆炸对距离炮孔中心越近的影响越大。

进一步得到不同条件下岩体内的有效应力峰值随距离的衰减关系，如图3所示。

结合图2和图3可以得出：

1)随着至炮孔中心距离的增大，应力峰值迅速衰减，且耦合装药无论在近处还是远处，其有效应力峰值的衰减程度均小于不耦合装药。这是因为不耦合装药时，空气间隔和药卷直径变小带来的装药量减小，直接降低了孔壁上的冲击压力。

2)同孔径条件下，耦合装药所达到的应力峰值远大于不耦合装药。以孔径35 mm为例，耦合装药时10 cm处的有效应力峰值为60.8 MPa，分别是炸药直径为29 mm、27 mm的1.67倍、1.91倍；在70 cm处，耦合装药的有效应力峰值为14.1 MPa，分别是炸药直径为29 mm、27 mm的1.96倍、2.47倍。当孔径为42 mm时，耦合装药10 cm处的有效应力峰值为76.3 MPa，分别是炸药直径35 mm、29 mm、27 mm的有效应力峰值的1.62倍、2.45倍和3.53倍；70 cm处，耦合装药的有效应力峰值为18 MPa，分别是炸药直径35 mm、29 mm、27 mm的有效应力峰值的2.07倍、4.5倍、6.4倍。

3)不耦合系数越小，在距中心不同位置所达到的有效应力峰值越大。从图3中可以看出，随着不耦合系数的增加，各监测点的有效应力峰值均减少。结合图2b)、e)、h)，炸药直径为29 mm时，孔径为32 mm在10 cm处的有效应力峰值为41.6 MPa，较之孔径为35 mm在10 cm处的有效应力峰值减少12.5%，较之孔径为42 mm在10 cm处的有效应力峰值减少25.2%。此外，不耦合系数为1.19和1.21、1.1和1.2两条曲线表明不耦合系数相近时，装药直径对有效应力峰值影响不大。

通过上文岩石损伤准则，代入公式(4)计算得到应力波达到14.7 MPa就会产生裂隙，所以在图3中添加了y=14.7 MPa的参照线，利用数据读取器得到各裂隙区边界；同时根据实测岩石力学性质，由公式(5)计算得到粉碎区和裂隙区的范围，得到表4和图4。

由表4和图4，理论计算和模拟得到的裂隙圈半径之间的误差基本在11%以内。通过图4可以看出：裂隙圈小的时候，理论值与模拟值基本一致，误差很小；而在裂隙圈较大时，理论值与模拟值相差较大；但其误差与理论值的占比基本一致。考虑到现场施工的经济性要求，根据理论计算和模拟出来的裂隙圈范围，利用公式裂隙圈面积除以炸药切面积，可以得到单位炸药的威力，上文已经得到耦合装药爆破效果比不耦合装药好很多，所以在此只考虑三种耦合装药的效果，经计算得炸药直径为32 mm、35 mm和42 mm的理论单位炸药(mm2)威力为285.82 mm2、310.76 mm2和369.19 mm2，模拟单位炸药威力为349.22 mm2、363.17 mm2和447.02 mm2。所以现场施工采用42 mm耦合装药爆破更优。

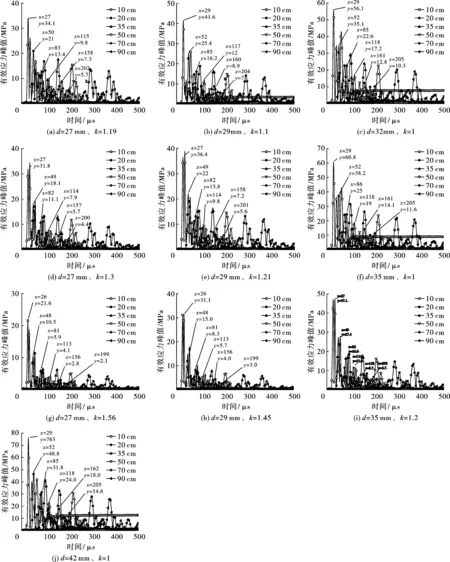
图 2 不同单元处的应力时程曲线

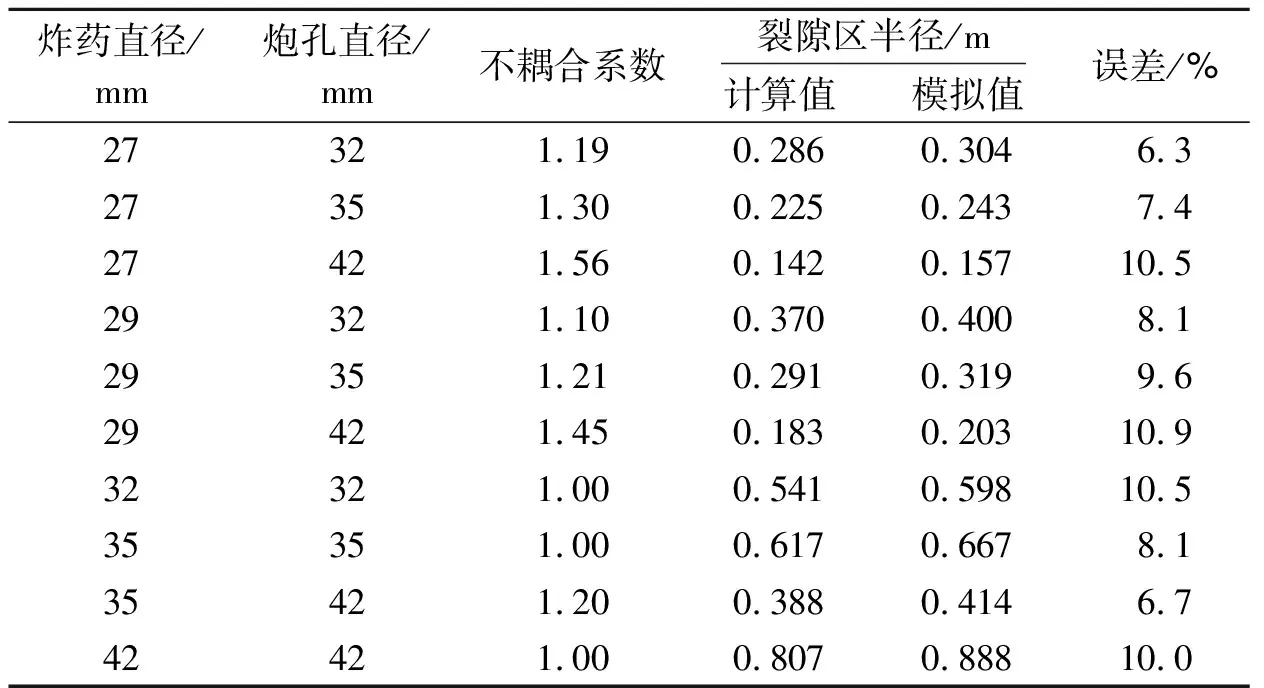
表 4 不同装药直径破坏范围

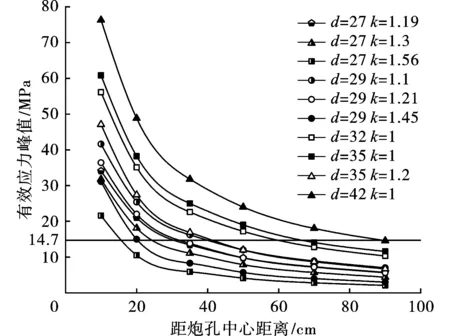
图 3 不同位置处的有效应力峰值与距炮孔中心距离的关系

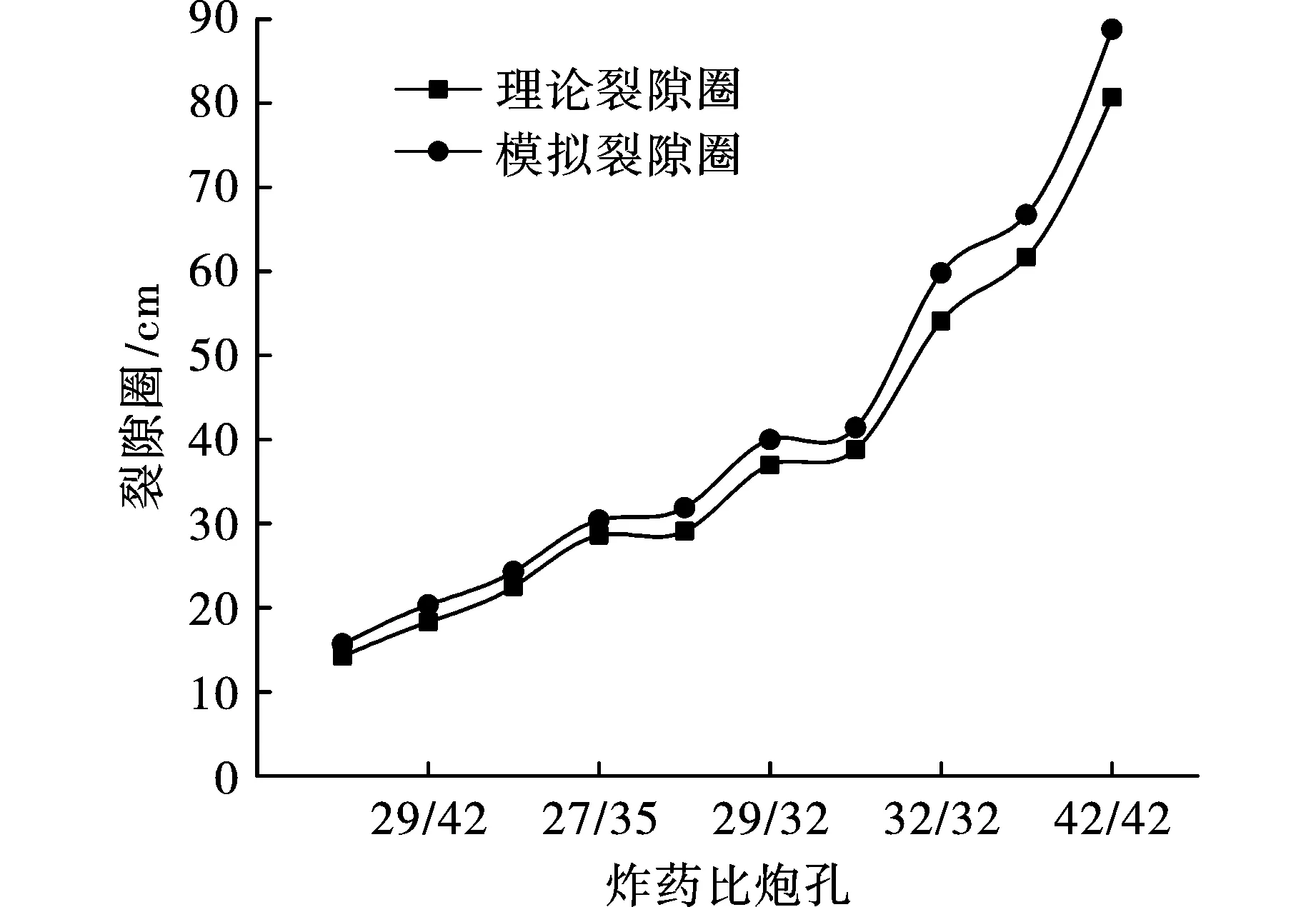
图 4 裂隙区半径模拟值与理论计算对比

4 结论

(1)耦合装药同一点的有效应力峰值大幅度大于不耦合装药，且岩石破坏范围也大于不耦合装药。

(2)随着距离炮孔中心的增大，有效应力波的峰值衰减逐渐变缓。

(3)不耦合系数越小，固定点的有效应力峰值越大，且不耦合系数对爆破范围的影响较之装药半径影响更大，因此可以通过调节不耦合系数节省炸药。

(4)模拟出来的破坏范围略大于理论计算的岩石破坏的范围，但基本吻合。且在42mm耦合装药爆破效果最佳。