平面平台型6-PSS并联机构构型选择与参数优化

王启明 张汉祖 蒋江月 宋 景 覃俊雄

(上海理工大学机械工程学院, 上海 200093)

0 引言

与串联机构相比，并联机构具有刚度大、承载能力强、运动精度高等优点，与此同时，6-PSS并联机构不同于传统Stewart并联机构，其驱动装置安装于基座而非连杆，因此6-PSS并联机构还具有惯性小、速度快、重心低等优点。

由于6-PSS并联机构的优越性能，其在众多领域得到了应用。胡圣鑫[1]鉴于星载SAR天线阵面调整机构刚度大、天线架背与阵面之间间距小、调整精度高等要求，选择了构型Ⅰ机构作为基础构型，将雅可比矩阵的条件数作为机构运动性能的评价指标，将全局误差系数作为机构运动精度的评价指标，通过优化得到了具有更高灵巧度和运动精度的设计参数。光电封装系统中的六自由度运动平台应具有行程大、精度高、稳定性好等特点，HOU等[2]提出采用柔性铰链的机构作为光电封装平台，并对其进行了逆运动学建模。郭抗等[3]根据光刻物镜中光学元件轴向调节机构轴向结构紧凑、调节精度高的使用需求，设计一种光学元件轴向调节机构，为提高机构可靠性和降低制作成本，将6-PSS并联机构中的6个运动支链分为3对，每对共用一个移动副，最后制作了样机，进行了试验验证；王宗平等[4]对提出的机构进行了动力学分析，该机构具有刚度高、运动精度高等优点。6-PSS并联机构的应用还有：仿生下颌平台[5]、送料机械手[6]、空间望远镜副镜调整机构[7]、地震模拟器[8]、仿生机械马[9]等。

工作空间、灵巧性等运动学性能是衡量一个机构优良的重要评价指标[10]。张伟中等[11]以规则圆台工作空间体积和全局运动/力传递性能为目标函数，通过粒子群算法对2-PUR-PSR并联机构进行了优化。孙小勇等[12]通过优化数学模型对6-PSS并联机构的工作空间和动力学特性进行了多目标优化。许允斗等[13]提出了一款构型为R(2RPR)R/SP-RR的五自由度混联机器人，并综合考虑工作空间与力传递效率等指标对其并联结构部分进行了关键尺度优化。李仕华等[14]提出了一种基于球面5R机构的空间二维指向机构，以工作空间、灵巧性和承载能力作为优化指标，采用图谱法对机构的结构参数进行了优化设计。HOU等[15]以3-PSS/S并联机构工作空间大小和性能为优化目标，采用遗传算法进行尺度参数优化。张良安等[16]提出改进混沌粒子群算法，并利用该算法对Ahut-Delta并联机构进行尺度优化。叶伟等[17]提出了一种用于微创手术的远中心并联机构，通过分析运动/力传递指标的性能，表明机构在工作空间内性能良好，以优质空间为目标对机构进行了尺度优化。目前，鲜有文献研究平面平台型6-PSS并联机构的构型选择与参数优化问题，该领域仍需深入研究。

本文主要考虑基座和动平台的球铰副中心分别位于同一平面上的平面平台型6-PSS并联机构，其构型选择与参数优化的本质是解决直线导轨在基座上的布置方式与尺寸综合问题。给出4种典型的平面平台型6-PSS机构构型，建立其运动学逆解模型并推导其雅可比矩阵，通过ADAMS仿真验证其正确性；对比分析4种典型构型机构的可达工作空间、转动能力和灵巧性，确定平面平台型6-PSS并联机构的最优构型；针对最优构型分析其结构参数对工作空间和灵巧性的影响规律，并以工作空间体积最大化为优化目标，得到最优结构参数值，并对优化后的机构进行误差分析，以期为平面平台型6-PSS并联机构提供设计依据。

1 平面平台型6-PSS机构运动学模型

1.1 机构描述与坐标系建立

本文研究的平面平台型6-PSS并联机构主要由基座(6个驱动电机、6条直线导轨、6个滑块)、下球铰、6条长度相同的连杆、上球铰、动平台等组成，通过电机驱动滑块运动，带动连杆从而实现动平台的六自由度运动。

结合图1对平面平台型6-PSS并联机构的4种典型构型进行说明。构型Ⅰ的导轨按照1-1-1-1-1-1分为6组，呈轮辐式布置，每条导轨的延长线通过基座中心；构型Ⅱ的导轨按照1-2-1-2分为4组，呈十字形正交布置，2个一组的导轨相互平行；构型Ⅲ的导轨按照2-2-2分为3组，呈120°对称布置，每组2条导轨相互平行；构型Ⅳ的导轨按照3-3分为两组，呈横向对称布置，每组3条导轨相互平行。

如图1所示，Ai、Bi(i=1,2,…,6)分别为动平台和滑块的球铰副中心；B0i为滑块初相位也就是滑块位移为0时的球铰副中心；Ai、B0i两两一组分为3组，分别均布在半径为r和R的圆周上，呈120°对称分布；每组动平台球铰副中心之间的夹角为θa；每组滑块球铰副中心之间的夹角为θb。6条连杆的长度均为L。6条直线导轨长度均为S0。4种构型的导轨布置方式不同，但结构参数相同。

如图1所示，以动平台中心为原点建立动坐标系OAXAYAZA，以基座中心为原点建立静坐标系OXYZ。

1.2 运动学逆解

并联机构逆解是已知动平台的位姿参数q=(x,y,z,α,β,γ)，反求6个滑块位移Si(i=1,2,…,6)，Si表示滑块球铰副中心Bi到初相位B0i的距离。动平台球铰副中心Ai在动坐标系中的坐标矢量A′i=(A′ix,A′iy,0)T可由机构几何参数得出，然后通过坐标变换公式得到其在静坐标系中的坐标矢量Ai=(Aix,Aiy,Aiz)T，坐标变换公式为

Ai=RA′i+T

(1)

其中

(2)

T=[xyz]T

(3)

式中R——旋转变换矩阵

T——平移变换矩阵

c表示cos，s表示sin。

滑块球铰副中心Bi(i=1,2,…,6)在固定坐标系中的坐标矢量Bi=(Bix,Biy,0)T可由机构结构参数和滑块位移Si得出。

根据运动过程中杆长长度不变，建立方程

‖Ai-Bi‖=L(i=1,2,…,6)

(4)

当位姿参数q=(x,y,z,α,β,γ)和机构结构参数已知时，求解式(4)可得到滑块位移Si。

1.3 机构雅可比矩阵

由刚体速度投影定理可知，连杆两端球铰副中心在连杆上的速度投影相等，以此建立等式。

第i个动平台球铰副中心的速度矢量为

VAi=VOA+ωA×(RA′i)

(5)

其中

式中VOA——动平台坐标原点速度矢量

ωA——动平台绕动坐标系转动角速度

动平台球铰副中心在连杆上的速度投影为

(6)

其中

Li=(Lix,Liy,Liz)T

式中Li——连杆方向向量

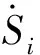
(7)

其中

mi=(cosθi,sinθi,0)T

式中θi——第i条导轨与X轴正方向的夹角

令VAiLi=VBiLi，则可得

(8)

式(8)中J6×6即所要求解的雅可比矩阵，反映了并联机构输入构件和输出构件之间的传动比。

1.4 误差模型

本文主要研究结构参数误差(驱动副安装位置误差、杆长误差、动平台球铰副安装位置误差)对机构末端位姿误差的影响，采用矢量微分法求误差模型，由矢量闭环公式可得

uili=RA′i+T-Bi

(9)

其中

ui=Li/li

式中ui——连杆方向单位向量

li——连杆实际长度

对式(9)两端进行全微分可得

δuili+uiδli=δRA′i+RδA′i+δT-δBi

(10)

参照文献[18]对式(10)进行推导和整理，得到结构参数误差和末端位姿误差的映射关系为

(11)

其中

δq=(δx,δy,δz,δα,δβ,δγ)T

式中 δq——机构末端位姿误差向量

δli——连杆长度误差向量

JP——杆长误差传递矩阵

JO——球铰副中心位置误差传递矩阵

δe——上下球铰副中心位置误差向量

1.5 运动学模型验证

以构型Ⅲ为例，设如表1所示结构参数。初始位姿q=(0,0,420,0,0,0)T，时间t∈(0,5 s)，给定动平台位姿变化函数

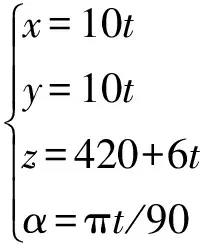
(12)

表1 机构的一组结构参数Tab.1 A set of parameter values of mechanism

利用Matlab位姿逆解求得上述给定过程的滑块位移和其速度变化曲线；利用ADAMS模拟机构运动得到仿真结果。将理论计算和运动仿真结果进行线性拟合[19]，结果如图2所示，二者位移最大误差量级为10-2mm，速度最大误差量级为10-2mm/s，均在允许范围之内，验证了理论模型的正确性。

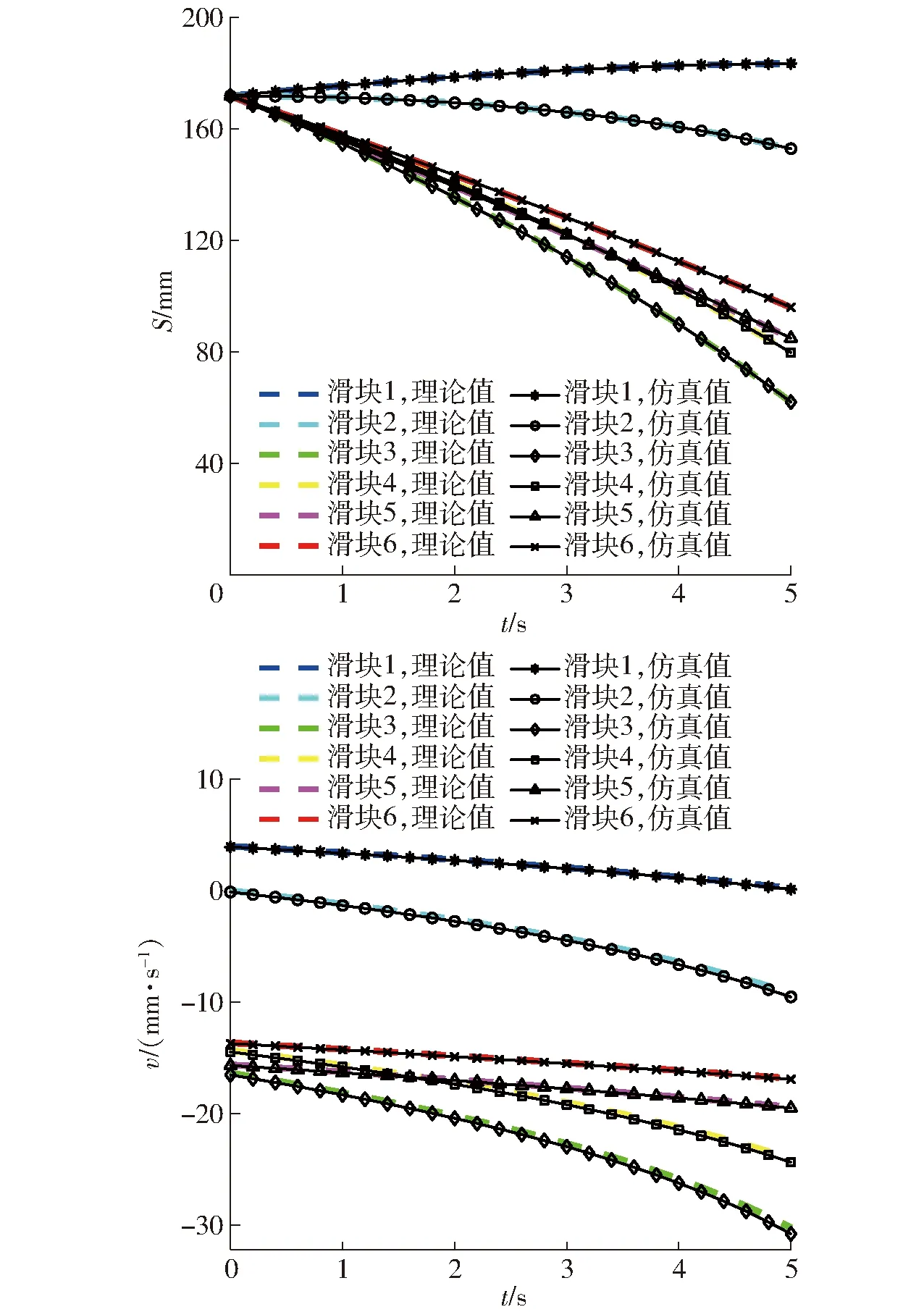
图2 理论与仿真结果对比Fig.2 Comparison of theoretical and simulation results

2 不同构型机构运动性能

2.1 工作空间

并联机构工作空间按照定义不同可分为完全工作空间、可达工作空间及灵活工作空间等[20]。考虑到六维工作空间很难描述，本文主要分析固定姿态角为(0°,0°,0°)下的可达工作空间。

工作空间的约束条件主要有以下两种：

(1)球铰副转角限制

球铰副转角φ定义为与球铰副连接的连杆方向向量和球铰副底座面的法向量之间的夹角。本文选择球铰副最大转角φmax=45°，则各球铰副的转角应满足

(13)

式中φai、φbi——动平台和滑块上各球铰的转角

nai——与动平台连接的球铰副底座面的单位法向量

nbi——与滑块连接的球铰副底座面的单位法向量

(2)滑块行程限制

受直线导轨长度限制，滑块在各自运行方向行程亦受限，其位移约束为

0≤Si≤S0

(14)

采用极坐标边界搜索法[21]求解可达工作空间边界。首先根据机构结构参数确定工作空间的最低边界点(0,0,Zmin)和最高边界点(0,0,Zmax)；其次用平行于XOY的平面将工作空间分为若干高度为Δz的子空间，在第i个子空间里，位置点的Z轴坐标为zi，极角σ从0开始以增量Δσ增加到2π，在每一个极角方向上，极径ρ从0开始以增量Δρ逐渐增加，直到位置点不满足约束条件则停止搜索，并记录下来该搜索方向的极径ρj；然后开始下一个极角方向的搜索，该方法求解的工作空间体积可表示为

(15)

图3为4种构型的机构可达工作空间及其投影轮廓图。由图3可知，4种构型机构在X、Y、Z方向可达工作空间范围分别为：构型Ⅰ 210、232、90 mm；构型Ⅱ 201、193、76 mm；构型Ⅲ 251、248、89 mm；构型Ⅳ 173、286、55 mm。

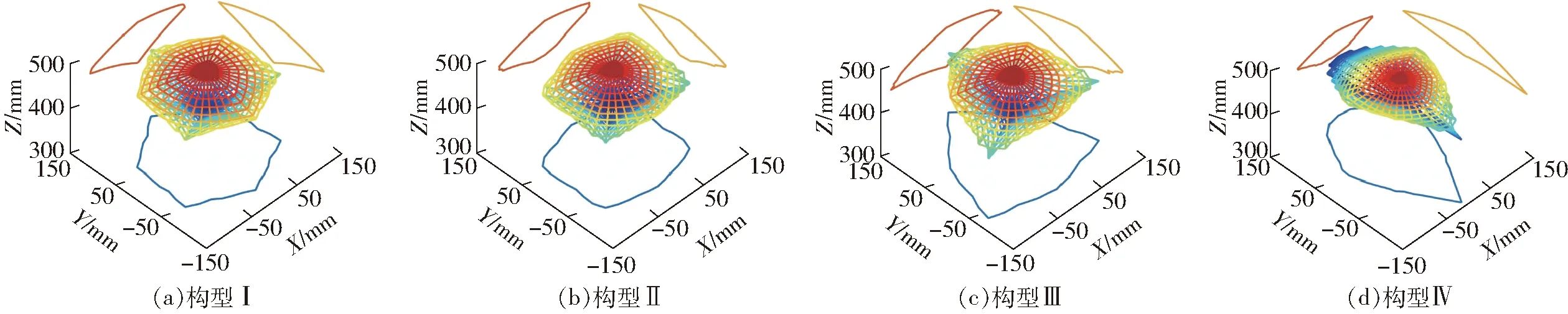
图3 4种构型的平面平台型6-PSS并联机构的可达工作空间及其投影图Fig.3 Reachable workspace and projection of 6-PSS parallel mechanism with planar platform

通过式(15)计算4种构型工作空间体积分别为1.084 5×106、9.789×105、1.222 1×106、6.668×105mm3。构型Ⅳ的工作空间体积相比于其他3种较小。构型Ⅲ在各方向上的可达工作空间范围和工作空间体积都相对较大。

2.2 转动能力

采用边界数值搜索法求解机构在不同高度工作空间平面上的所能达到的最小转角和最大转角。由于机构具有对称性，因此只需对比绕X轴转角α，工作空间k处的高度Hk为

Hk=Zmin+k(Zmax-Zmin) (0≤k≤1)

(16)

如图4所示，构型Ⅳ的转动范围略不同于其它3种构型。构型Ⅰ、构型Ⅱ、构型Ⅲ在各自工作空间高度1/2处到3/4处之间转动范围达到最大，绕X轴转角α为[-18°,18°]，从图4可知，前3种构型的转动能力相差不大。

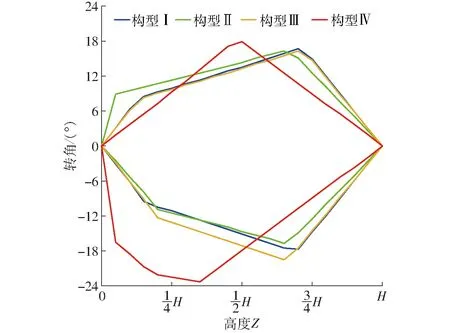
图4 4种构型的机构在不同工作空间高度上的绕X轴转角α范围Fig.4 Comparison of rotation capacity between different configurations

2.3 灵巧性

雅可比矩阵条件数K(J)可定量反映机构输入与输出之间运动/力传递关系。通常1≤K(J)≤∞，一般采用雅可比矩阵条件数的倒数来表示机构局部灵巧度，条件数越小，灵巧度越大，机构运动/力传递性能越好[22]。局部灵巧度指标计算式为

(17)

由于LCI只能判断机构在单个位形下的运动/力传递性能，利用全局灵巧度指标GCI来评价机构在整个工作空间里的运动/力传递性能，计算式为

(18)

式中n——工作空间内离散点的数量

图5 4种构型的6-PSS并联机构的灵巧度分布图Fig.5 Distributions of dexterity of four configurations of 6-PSS parallel mechanism with planar platform

图6 不同结构参数对可达工作空间的影响Fig.6 Influence of different structural parameters on reachable workspace

综上可知，构型Ⅲ可达工作空间范围、工作空间体积、不同工作空间高度上的灵巧度分布、全局灵巧度都较优越，因此本文采用最优构型Ⅲ的6-PSS并联机构。

3 结构参数优化设计

3.1 结构参数

图6为6个结构参数工作空间在Y=0平面上的投影轮廓图。单个结构参数改变，对工作空间投影的影响趋势如表2所示。

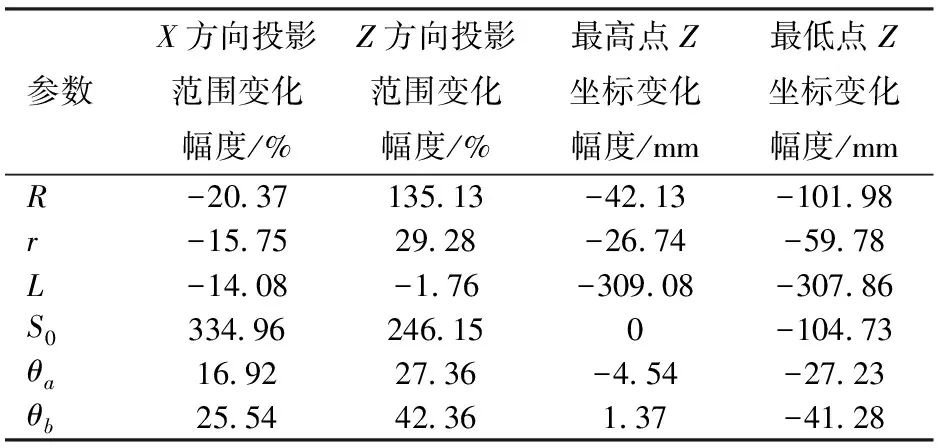
表2 工作空间投影范围的变化趋势Tab.2 Variation trend of workspace projection

由图6和表2可知，R增大，工作空间在X方向的投影范围减小，在Z方向的投影范围显著增大，最高点下移，最低点显著下移，当R增大到一定值，工作空间最低位置不再下降，且由一点变为一个平面；由图6和表2可知，r减小，工作空间在X方向的投影范围减小，在Z方向的投影范围增大，最高点下移，最低点下移，当r减小到一定值，工作空间最低位置不再下降，且由一点变为一个平面；由图6和表2可知，L减小，工作空间整体下移，工作空间在X方向和Z方向投影范围变化较小，当L减小到一定值，工作空间最低位置由一点变为一个平面；由图6和表2可知，S0增大，工作空间投影最高点无变化，工作空间在X方向和Z方向的投影范围都显著增大，当S0增大到一定值，工作空间最低位置不再下降，且由一点变为一个平面；由图6和表2可知，θa增大或θb减小，工作空间在X方向和Z方向的投影范围增大，最高点位置几乎不变，最低点下移。

上文所述及图6中工作空间最低位置为一点的情况如图7所示，当所有滑块都到达最大行程时，动平台下降到最低点。工作空间最低位置为一个平面的情况如图7所示，球铰副转角已达到最大值，但所有滑块尚未达到最大行程，此时滑块仍可移动，从而工作空间最低位置形成一个平面。结构参数改变，当R越大、r越小、L越小、S0越大时均会出现不同程度的最低平面。

为了优化构型Ⅲ的结构参数，通过式(15)、(18)计算机构的工作空间体积和全局灵巧度，由此分析判断各结构参数对性能指标的影响。如图8a～8d所示，可知在一定的结构参数范围内，工作空间体积V和全局灵巧度GCI呈正相关。如图8e、8f所示，θa、θb对全局灵巧度GCI影响较大，但是对工作空间体积V影响较小。

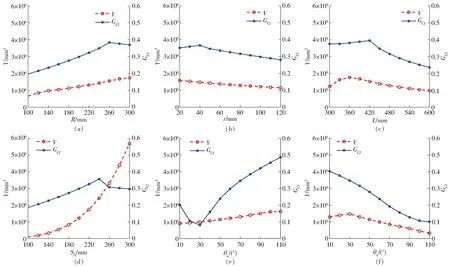
图8 结构参数与性能之间的关系Fig.8 Relationships between structural parameters and performance

究其原因，由第2.3节可知，如图5所示，工作空间内的点，其纵坐标Z越小，局部灵巧度LCI越大; 由图6、 8可知，机构结构参数改变(R增大，r减小，L减小，S0增大)，工作空间均增大，主要是工作空间偏下部分体积增大所致；工作空间逐步偏下，纵坐标Z减小，局部灵巧度LCI越大，而偏下部分体积越大，则高的局部灵巧度LCI比例增大，全局灵巧度GCI越大。随着结构参数在给定范围内继续变化，出现了工作空间最低位置为一个平面的情况，此时工作空间增大变缓，而工作空间偏下部分体积又逐步减小，全局灵巧度开始减小且拐点之后工作空间体积和全局灵巧度不再呈正相关。

在参数优化时，确保机构在每组结构参数下的工作空间最低位置是一个点，即可保证工作空间体积和全局灵巧度正相关，此时只需将工作空间体积作为优化目标，就可得到工作空间大、全局灵巧性好的结构参数。

3.2 优化模型

工作空间体积V作为优化目标函数，可由式(15)计算得到。选取机构的结构参数为设计变量。为了参数优化的标准化和普适性[23]，取导轨长度为固定值S0=200 mm，其他设计变量变化范围如式(19)所示，则优化模型为

(19)

3.3 优化结果

采用粒子群算法求解上述优化问题。该算法中，粒子拥有记忆功能会记录自身最优位置，受到自身经验的引导，同时基于信息共享机制受到群体经验的影响，使得粒子同时具有向自身最优位置和全局最优位置逼近的趋势，具有较好的全局搜索能力和收敛速度[24]。粒子群算法的控制参数设置为：种群规模40，最大迭代次数80，学习因子1和2都取1.5，惯性权重为0.4～0.8。结构参数优化设计的圆整结果如表3所示，其中解1和解2为挑选的局部最优解，解3为全局最优解。

3个解所对应的工作空间投影图如图9所示，可知工作空间体积增大主要是由于竖直Z方向的可达范围增加。3个解所对应的灵巧度分布如图10所示，可知同比例的工作空间高度Z所对应的灵巧度亦增大。由表3可知，随着工作空间体积增大，全局灵巧度也增大，验证了工作空间体积和全局灵巧度正相关的结论以及优化模型的正确性和有效性。

表3 优化结果对比Tab.3 Comparison of optimization results

图9 优化结果对应的工作空间投影图Fig.9 Workspace projection maps of optimization results

解3对应的机构三维模型如图11所示。3个解的共同点是动平台上每组的两个球铰副之间的距离等于每组的两条直线导轨之间的距离，即满足2rsin(θa/2)=2Rsin(θb/2)。

综上所述，结合优化结果可得出平面平台型6-PSS并联机构的设计原则。首先，按照构型 Ⅲ 布置直线导轨，具体为2-2-2分为3组，呈120°对称分布，每组的两条导轨相互平行；然后，由实际应用需求决定导轨长度S0，需获得较大工作空间，则选用较大导轨末端布置圆周半径R和较小的动平台球铰副布置圆周半径r；通过调整连杆长度L，来使工作空间最低位置为一点，即动平台在最低位置时，球铰副转角小于最大转角；通过调整每组动平台球铰副夹角θa和每组导轨末端夹角θb，来满足2rsin(θa/2)=2Rsin(θb/2)，即可得到运动性能优越的平面平台型6-PSS并联机构。本文为平面平台型6-PSS并联机构的设计提供了依据。

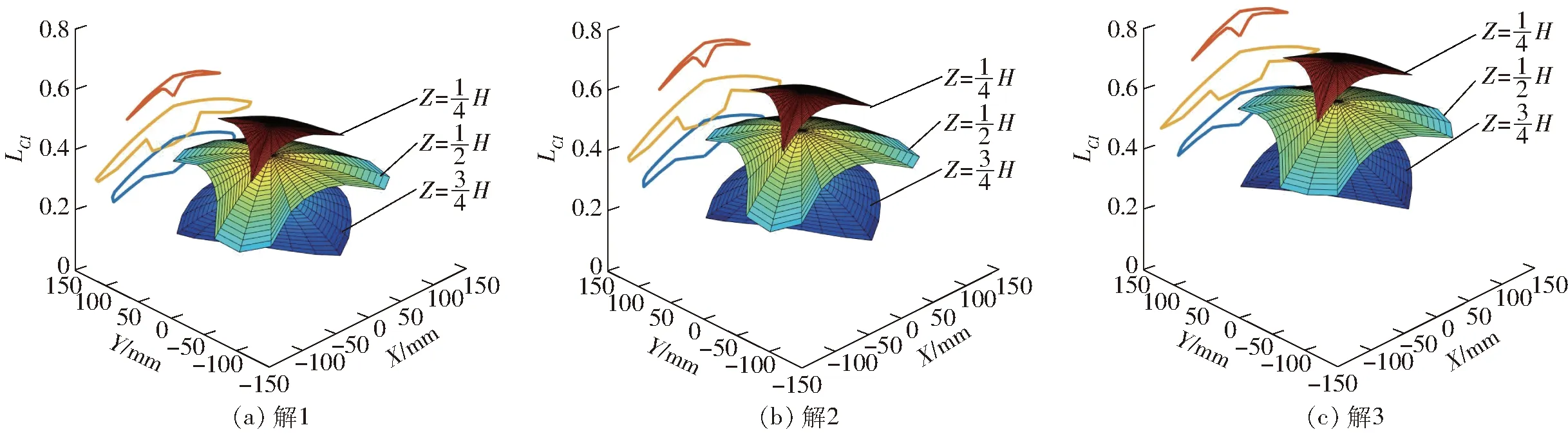
图10 结构优化结果所对应的灵巧度分布Fig.10 Distributions of dexterity of optimization results

图11 最优结构参数对应的三维模型Fig.11 3D model correspond to optimal structural parameters

3.4 误差分析

由于零件制造和机构装配水平的限制，实际结构参数与理论结构参数不可避免地存在误差[25]。并联机构误差来源有驱动误差、间隙误差、变形误差等。本文主要研究结构参数误差，如驱动副安装位置误差δRi、δθb、杆长误差δli、动平台球铰副安装位置误差δri、δθa。

由式(11)可知，任意一条支链有5项结构参数误差，共有30项结构参数误差，数量较多且不易同时进行分析，所以本文将研究单条支链上单项误差对机构末端位姿误差的影响，设长度误差为0.2 mm、角度误差为1°，取机构在工作空间内代表机构升降、平移、俯仰、偏航等运动的几个位姿点，应用Matlab进行仿真计算，结果如表4所示。

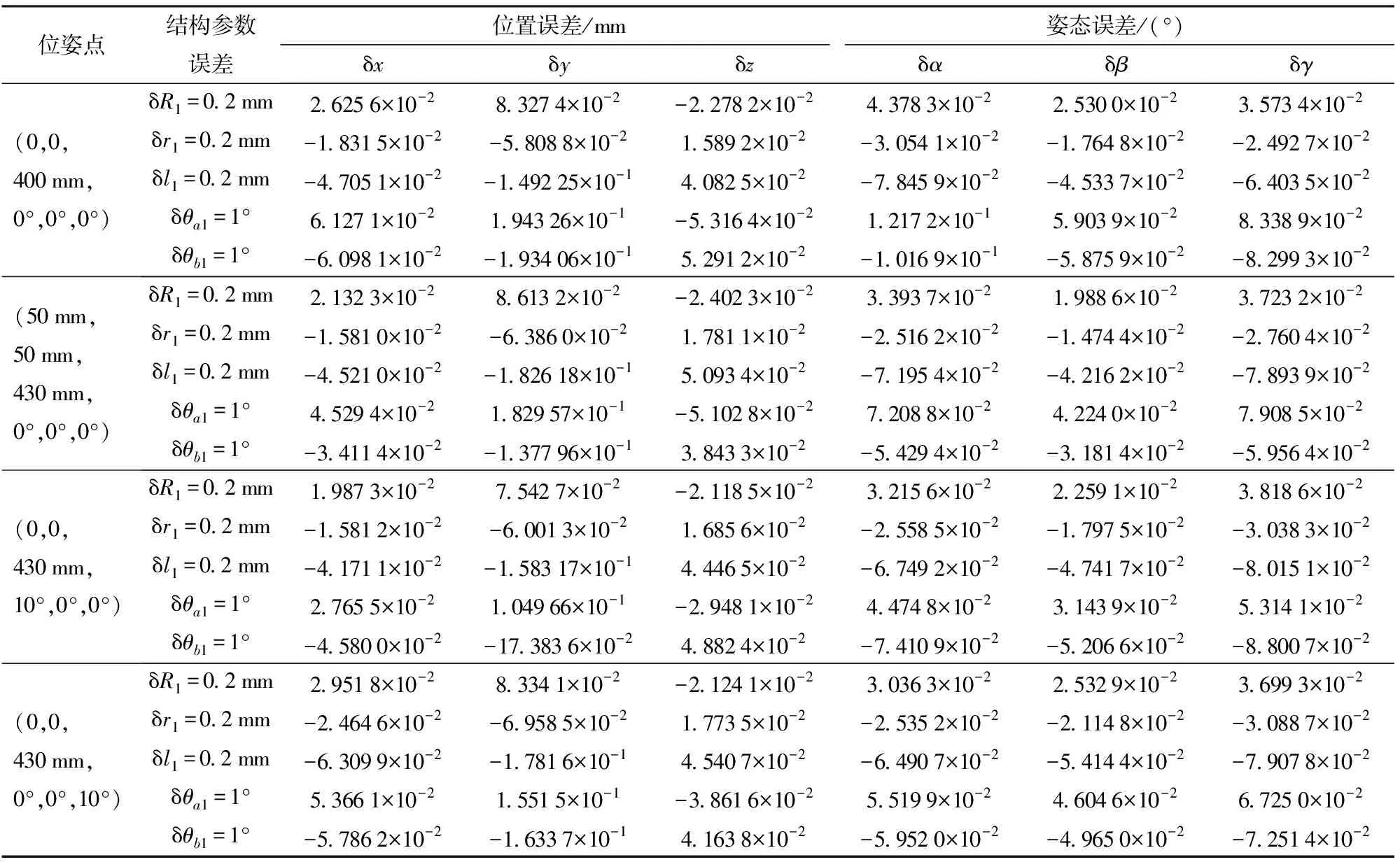
表4 单支链上单项误差对机构末端位姿误差的影响Tab.4 Influence of structural parameter error on pose error of mechanism end

由表4可知，杆长误差和上、下球铰副中心位置误差都是影响机构末端位姿误差的主要因素。不同位姿点对结构参数误差的敏感度不一样，但总的来说，杆长误差δli对机构末端位姿误差的影响大于导轨末端布置圆周半径误差δRi的影响大于动平台球铰副布置圆周半径δri的影响。

4 结论

(1)针对4种典型的平面平台型6-PSS并联机构构型，根据坐标变换及机构几何关系，建立了运动学逆解模型，通过刚体速度投影定理，推导了机构的雅可比矩阵，通过矢量微分法建立了误差模型，并采用ADAMS仿真，验证了运动学模型的正确性。

(2)绘制了4种构型的平面平台型6-PSS并联机构的工作空间图和灵巧度分布图，求解了工作空间体积V和全局灵巧度GCI，经过对比分析得出构型Ⅲ的性能最优。

(3)分析了构型Ⅲ的结构参数对其工作空间和灵巧性的影响规律，结果表明在一定的结构参数范围内，工作空间体积和全局灵巧度正相关。

(4)以工作空间体积为优化目标函数，以机构结构参数为设计变量，通过粒子群优化算法求解，得到了最优结构参数，并与其他局部最优解结构参数进行对比，验证了优化结果的正确性，并对优化后的机构进行了误差分析，为平面平台型6-PSS并联机构的设计提供了依据。