双模融合6-[(RPRRRP)R-R]US并联机构运动学分析

陈宇航 赵铁石 郭建纲 陈丽缓 郝增亮

(1.北华航天工业学院机电工程学院， 廊坊 065000；2.燕山大学河北省并联机器人与机电系统实验室, 秦皇岛 066004;3.燕山大学先进锻压成形技术与科学教育部重点实验室, 秦皇岛 066004)

0 引言

多任务协同、多模式融合是机械装备发展的趋势。为应对复杂的实际应用，机构学领域涌现出一系列新颖的机构形式，如可重构机构、并联冗余自由度机构和含有子闭环的机构等。并且针对多模式并联机构、多任务融合机构、一机多用等方向开展了较多研究。

关于可重构机构、多模式机构等研究成果较多，戴建生团队[1-2]首先阐述了变胞机构的机理和应用，并对相关研究进展进行了系统梳理；于靖军等[3]论述了多模式机构的研究进展以及未来应用的可能；单彦霞等[4]基于TCI指标提出一种能实现多模式机构操作模式平稳切换的方法。刘伟等[5]基于自由度可变的混联支链综合了一类多模式机构，能实现3种运动模式间的变换。沈惠平等[6]提出了一种动平台可重构的三自由度并联机构，具有部分运动解耦性。邹琦等[7]设计了一种运用离合器与齿轮系配合完成机架重构过程的并联机构。石志新等[8]采用方位特征集法对四自由度双模式机构展开综合，并对其中一种进行位置分析。具有冗余自由度的机构，运动输出具有更多可能性。QU等[9-10]提出一种具有冗余自由度的平面机构，并进行了运动学和奇异性分析；ZHAO等[11]提出一种具有冗余自由度的并联机构，由于运动的冗余特性使该机构具有非常大的转角工作空间；GOSSELIN等[12-14]先后提出一类新型的具有转动能力不受限制的平面冗余自由度并联机构，以及一类能够通过冗余特性消除奇异位形并增大转动工作空间的空间机构。在分支中引入子闭环机构，可以改善空间机构性能，并能够合理引入冗余自由度。LI等[15-16]对一类分支含子闭环的并联机构进行研究，通过在分支内引入子闭环综合一类少分支多自由度形式的并联机构，并为步行机器人设计了一种含闭环结构的支腿；朱小蓉等[17]综合了一类分支中含有双驱动五杆闭环回路的并联机构，并提出了7种耦合度为0的回路。文献[18-19]面向调姿隔振应用，在并联机构的分支中引入子闭环机构使原机构具有冗余自由度，并通过子闭环实现高低频混合输入。

多模式机构更多关注不同模式间的切换，而多模式融合应用在实际工程中应用同样广泛，本文拓展多模式机构的范畴，设计一种分支内含有六杆子闭环输入单元的新型并联机构，通过解析与数值相结合的方法对机构进行运动学分析，以期实现“高频低幅值”与“低频大幅值”两种模式运动的融合。

1 机构形式

在6-RUS并联机构中，各分支转动副R为输入。通常对输入副R的实际驱动形式有电机直接驱动和四杆机构间接驱动，如图1所示直接驱动形式，运动学计算相对简单，但动力学性能较差；间接驱动形式，运动学分析较复杂，但动力性能较好。

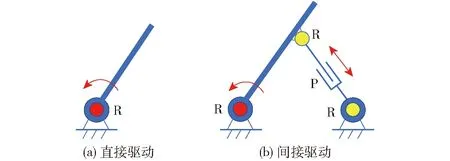
图1 转动副R的驱动形式Fig.1 Driving forms of rotating pair R

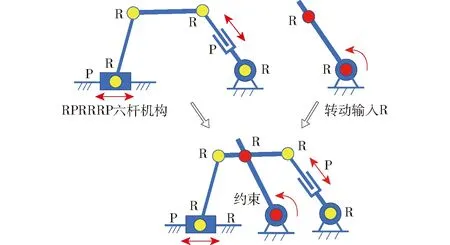
图2 双输入单元组成原理Fig.2 Dual-input unit composition principle

为实现动平台双模融合运动，对驱动副R的驱动形式进行双模融合输入设计，其实现形式为在驱动副杆件的适当位置，通过另一个转动副R′与一个平面六杆子闭环机构(RPRRRP)连接，构成双输入单元如图2所示；也可以将该设计理解为将驱动副R替换为一个局部并联机构，该局部并联机构包含一个驱动分支和一个约束分支，其中约束分支只包含一个R副，驱动分支为包含一个平面六杆机构的混联分支，形式为(RPRRRP)R。

根据Kutzbach-Grübler公式[20]计算可得(RPRRRP)R-R双输入单元的自由度为2，需要两个输入，机构才能有确定运动。以两个P副为实际输入，它们分别对应两种运动模式的驱动，因此通过双输入单元的输出杆可实现双模运动融合。

通过上述方法实现双模融合输入后，机构形式为6-[(RPRRRP)R-R]US，如图3所示。显然双输入局部并联机构的输出杆件即为原6-RUS机构的原动件，且运动形式仍为原输入副R的转动，因此对于动平台，约束形式与6-RUS相同，所以动平台仍能实现空间六自由度运动。对于6-RUS机构，此时驱动副R的输入中包含两种成分，分别对应双输入子闭环中两种性质的驱动，可根据应用需求进行组合。每个[(RPRRRP)R-R]US分支需要双输入，总体机构才能具有确定运动，因此6-[(RPRRRP)R-R]US并联机构自由度数为12，输入数大于末端构件自由度数，属于运动冗余并联机构。

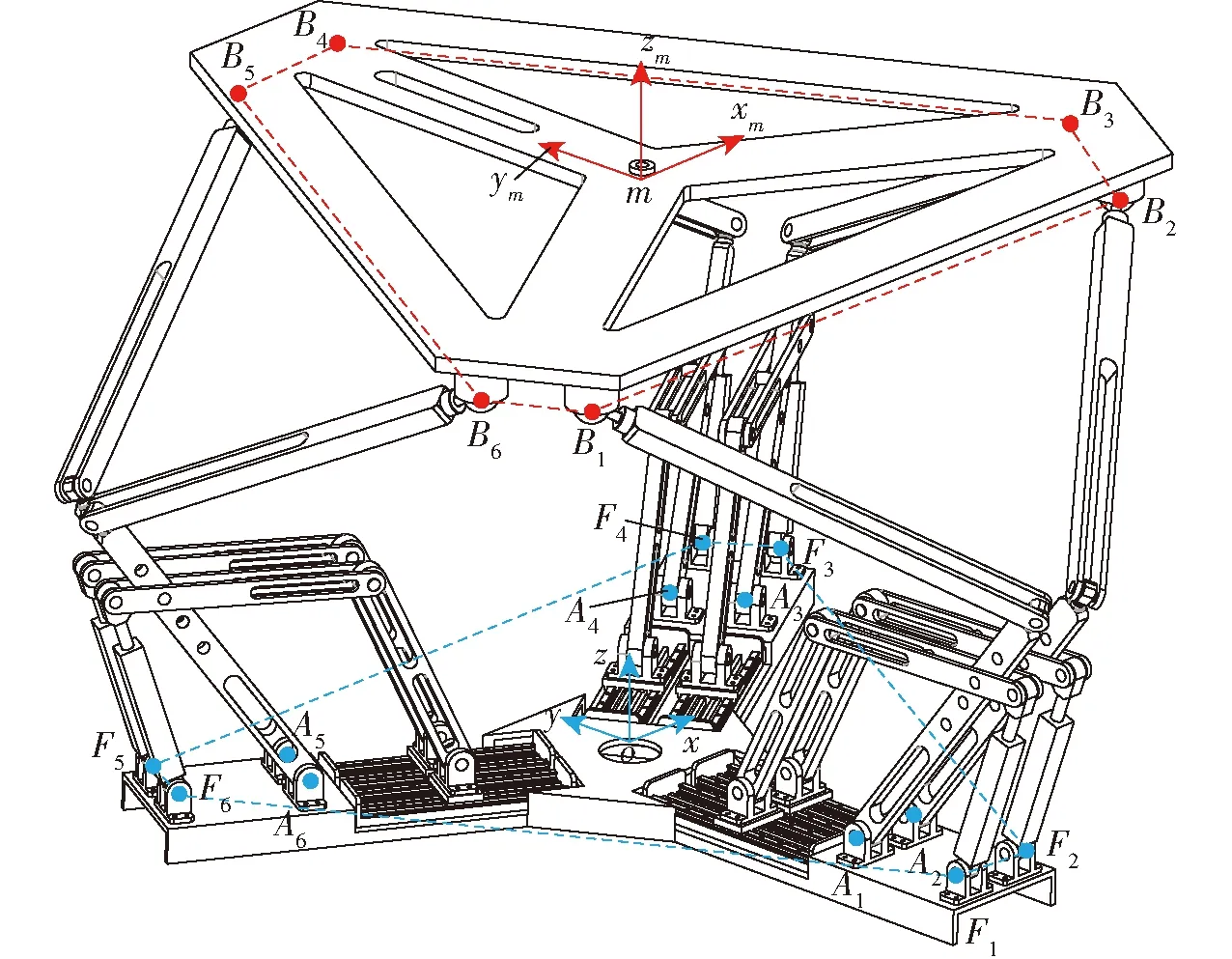
图3 机构形式及坐标系Fig.3 Mechanism form and coordinate system

对该机构的分析，可以将机构划分为内、外两层，内层机构：(RPRRRP)R-R双输入子闭环机构；外层机构：6-RUS。内、外层机构通过共同的R副实现运动和力的传递。

2 单模式机构运动学反解分析

机构由动平台、基座和6条形式相同的分支组成，每条分支与上平台通过球副连接，铰接点记为Bi，其中i为分支标号，i=1,2,…,6；分支底部与基座通过2个R副和1个P副连接，其中2个R副的铰接点记为Ai、Fi。在Ai、Fi所在平面的几何中心建立基坐标系{o},在Bi所在平面的几何中心建立动平台坐标系{m},如图3所示。

每个分支中包含两个驱动副，通过锁定其中一个驱动，可让机构工作于单一运动模式，以灵活适应不同应用场景。

双输入子闭环机构简图如图4所示，将左侧移动副设定为调姿驱动，对应一类低频大行程驱动器，例如电动缸、液压缸等；右侧水平移动副设为振动驱动，对应一类高频小行程驱动器，如作动器、高频直线电机等。

2.1 调姿模式运动学反解

当振动驱动被锁定，机构仅实现低频小幅值的位姿运动。机构的运动学反解分为两步：①对外层6-RUS并联机构进行反解求得各分支输入角θi。②建立内层驱动子闭环的运动学方程，根据θ求得实际驱动l1。

步骤(1)：不考虑驱动子闭环RPRRRP，外层机构形式为6-RUS，分支简图如图5所示，建立分支坐标系{i}，R副与基座铰接点Ai为坐标原点。

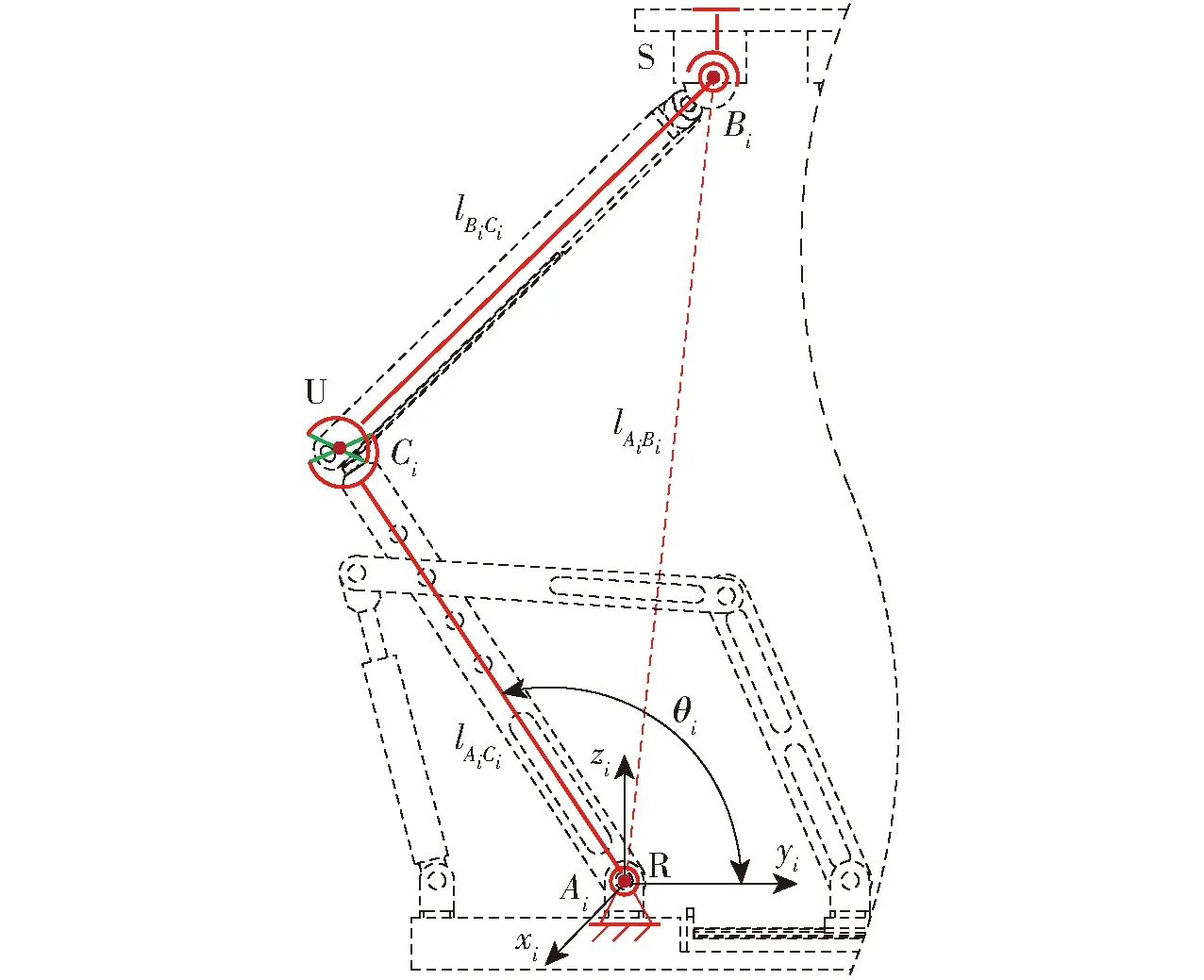
图5 RUS单分支简图Fig.5 Simple diagram of single branch of RUS

根据杆长约束关系可得

(1)

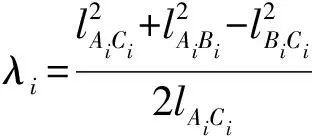
(2)

式中lAiBi、lAiCi、lBiCi——杆AiBi、AiCi、BiCi的长度

xBi、yBi、zBi——铰链点Bi的坐标

步骤(2)：双输入单元机构简图如图6所示。由于任意分支内双输入单元的计算过程相同，为了表达式简洁，除驱动变量外，其余忽略分支下角标i。

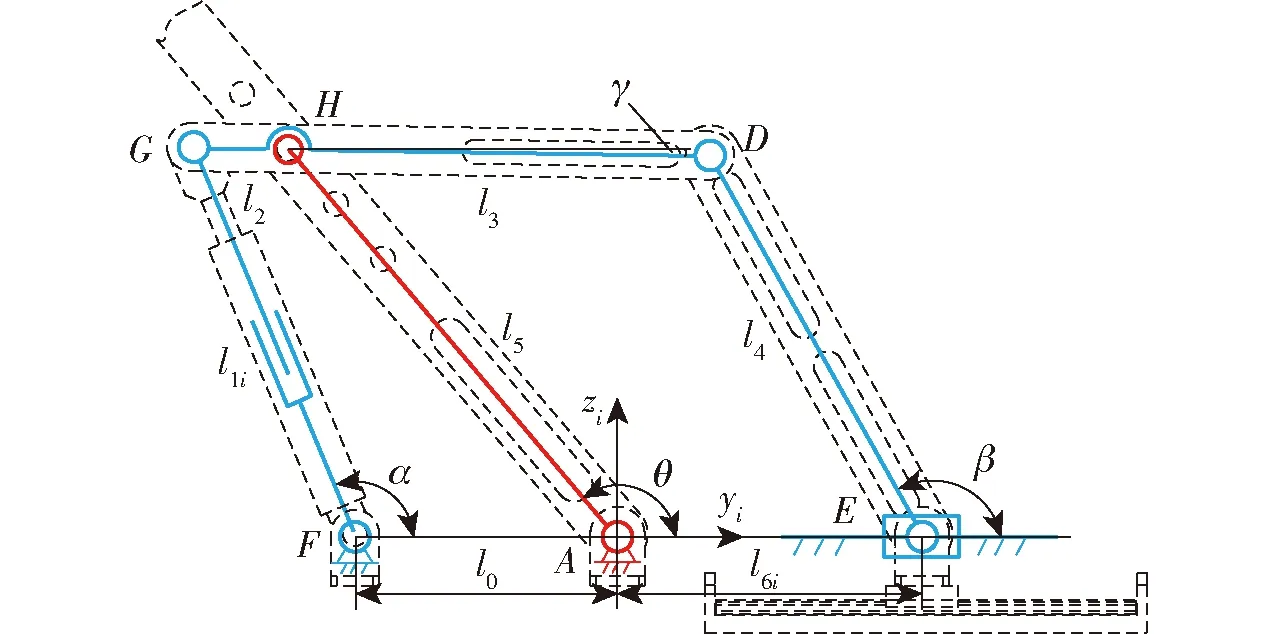
图6 双输入子闭环机构简图Fig.6 Mechanism diagram of dual-input sub closed loop

图6中，l1i、l6i(i=1,2,…,6)是两个驱动尺寸，即第i分支内FG、AE长度，l0、l2、l3、l4、l5分别为杆FA、GH、HD、DE、AH的长度，α为FG与水平方向夹角，β为杆DE与水平方向夹角，γ为杆GD与水平方向夹角。在调姿运动模式下，l1是变量，l6是定值。

根据几何关系建立双输入子闭环机构的矢量封闭方程

l5+l3=l6i+l4

(3)

解得

(4)

其中

(5)

式中ku1、ku2、ku3——中间系数

点D和点H坐标为

(6)

(7)

令

(8)

式中yG——点G的y轴坐标

zG——点G的z轴坐标

K——杆GD斜率

由杆长l2约束关系可得

(9)

驱动量尺寸FG的长度关系式为

(10)

将式(8)、(9)所求值代入式(10)，即求得此时的实际驱动量l1i。

2.2 振动模式运动学反解

当调姿驱动被锁定，机构输出六维振动。此时图6中，l1i是固定值，l6i是变量。其运动学反解同样分两步，步骤1与调姿模式相同，参照式(1)；步骤2为根据θ求得实际驱动l6i。

类似调姿运动求解过程可得α与θ的关系式为

(11)

其中

(12)

式中kv1、kv2、kv3——中间系数

点D坐标表示为

(13)

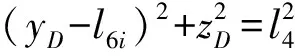
(14)

当动平台位姿已知，由步骤(1)求得外层机构6-RUS驱动角θi，然后根据式(11)、(13)依次求得角α和点D坐标，最后通过式(14)解得振动模式的驱动输入l6i。

3 双模式融合运动学反解分析

机构进行双模融合运动时，驱动输入个数为12，动平台输出运动自由度数为6，属于自由度冗余机构。对于给定位姿，可以得到无穷多组反解。结合一般实际应用工况，设定两种反解求解策略，使得到的反解具有更为明确的实际意义，具体如下：

任意时刻t，动平台输出的融合运动位姿，可分解为两种成分：低频大范围的位姿运动和高频小幅值的振动，即

W(t)=Wu(t)+Wv(t)

(15)

式中W——双模式融合运动位姿

Wu——位姿运动成分

Wv——振动成分

双模融合运动可理解为一种平衡位置不断改变的振动，变化的平衡位置即是位姿运动。因此在反解计算中，可以设定两种驱动求解分配策略：

(1)先Wu(t)后Wv(t)：先求平衡位置后叠加振动

先求解任意时刻t平衡位置Wu(t)的对应的反解输入，即调姿输入，再以Wu(t)为当前平衡位置，求解机构从Wu(t)运动到W(t)的位姿反解，即振动输入，过程如下：

假定各分支内振动输入l6i在驱动中位锁定，l6i的中位值作为求解l1i时一项固定的结构参数。以Wu(t)为目标位姿计算任意时刻t调姿输入的值，即

L1(t)=L1(0)+u(t)

(16)

其中

(17)

式中L1——调姿输入矢量

u——调姿输入增量矢量

ui——l1i的增量

以Wu(t)为当前位姿，Wu(t)+Wv(t)为目标位姿，L1(t)为结构参数，根据振动模式的反解过程计算该t时刻振动驱动尺寸为

L6(t)=L6(0)+v(t)

(18)

其中

(19)

式中L6——振动输入矢量

v——振动输入增量矢量

vi——l6i的增量

在求L6的过程中，L1为时变结构参数，t时刻对应的值为L1(t)。

(2)先Wv(t)后Wu(t)：先求振动再改变平衡位置

以初始位置为平衡位，求解任意时刻t的振动位姿Wv(t)所对应的输入，即振动输入，再求每一时刻，机构从Wv(t)运动到Wu(t)+Wv(t)对应的反解输入，即调姿输入。该策略为策略(1)的对偶过程，具体步骤为：

先锁定L1以其为固定参数，并以Wv(t)为目标位姿，计算任意时刻振动输入L6(t)，再以L6(t)为瞬时结构参数，t时刻，以Wv(t)为初始形位，W(t)为目标形位计算L1(t)。

需要注意两点：①两种求解策略的先后顺序仅是计算逻辑的先后，实际操作时，任意时刻计算得到L1(t)和L6(t)后，两者同时输入系统。②相同位姿下，两种策略计算的双输入结果不同，设定的两种策略所解算出的是机构无穷多组解中的两组，但调姿输入和振动输入各自的反解模型不变。

4 机构运动学正解分析

已知机构的实际输入L1(t)、L6(t)，求动平台的位姿W(t)为机构正解。由于各分支内存在子闭环机构，因此机构正解同样需要分两步完成。

(1) 内层子闭环机构正解

任意分支i内，外层机构6-RUS的分支驱动角θi是关于l1i、l6i的函数，然而θi=f(l1i,l6i)的解析解难以获得。因此采用数值方法求取。当l1i确定，θi随l6i变化呈单调递增关系，因此可以把l1i先给定，采用二分法迭代对比l6i，最终获得满足误差允许要求的解。求解过程如图7所示。

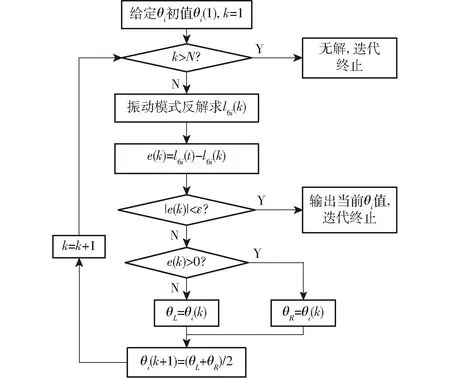
图7 内层子闭环正解流程图Fig.7 Process of positive solution in sub-closed loop

图7中，N为最大迭代次数；e(k)为l6i第k次迭代误差，θL、θR为当前循环下θi取值的边界；ε为设定的求解精度。

(2)外层6-RUS机构正解

根据各分支子闭环内实际驱动，通过步骤(1)求得子闭环输出杆的转角θ，即外层6-RUS机构分支的驱动角。对于6-RUS机构，全部输入θi已知，求动平台的位姿W(t),为机构正解过程。

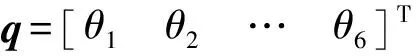
q=f(W)

(20)

方程组(20)为非线性方程组，根据输入q求位姿W，解析方法难以求解，因此考虑采用数值法。为了让求解过程快速收敛，可采用牛顿法[21]，迭代方程为

Wk+1=Wk+G(Wk)qΔk

(21)

其中

qΔk=q-f(Wk)

(22)

式中Wk——第k次迭代位姿

qΔk——q的第k次迭代误差

G——机构一阶影响系数

外层6-RUS机构正解流程如图8所示。

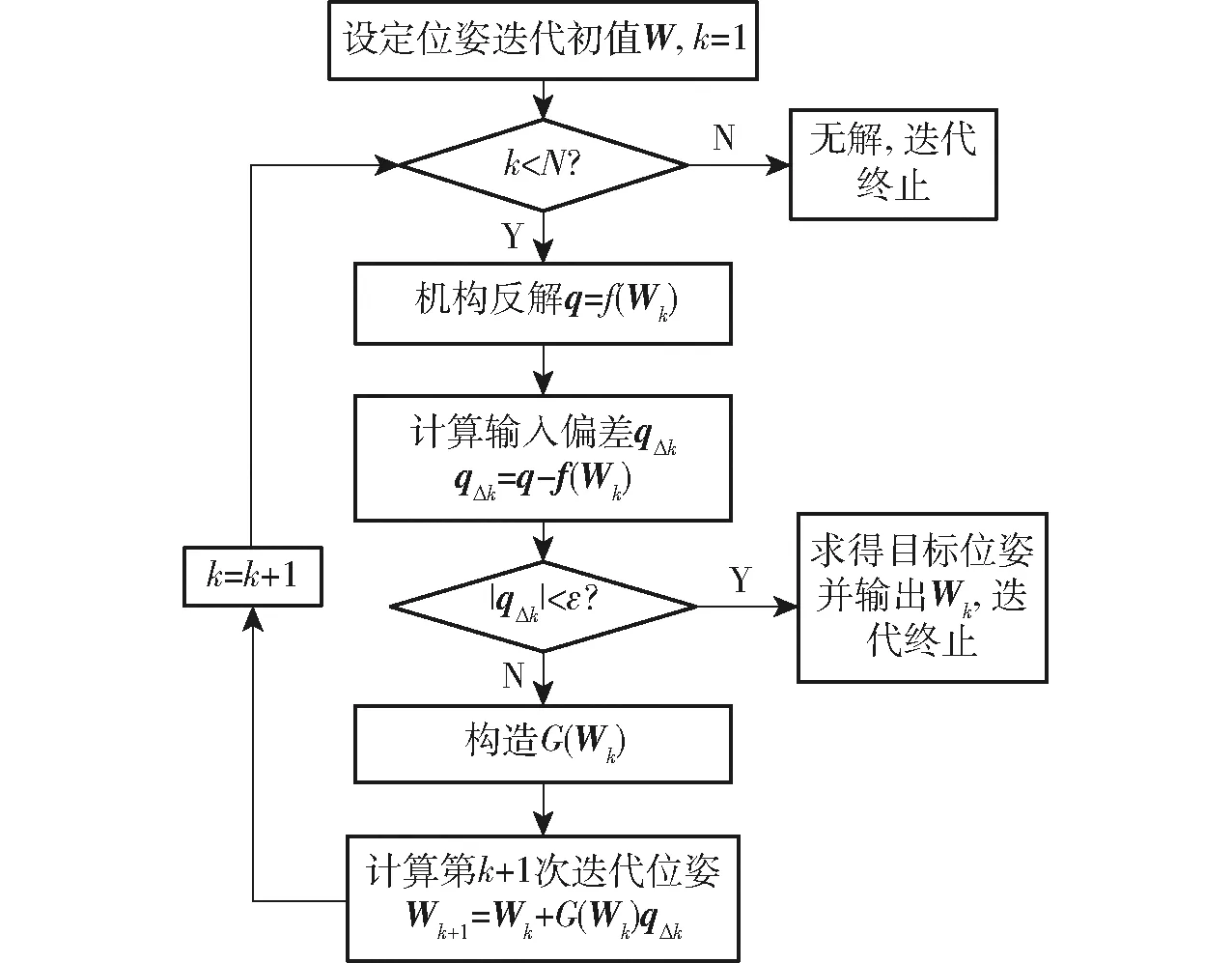
图8 6-RUS机构正解流程图Fig.8 Process of forward solution of 6-RUS mechanism

5 数值算例与仿真

通过理论模型计算和运动学仿真分别对上述理论分析正确性进行验证。不同的反解分配策略得到仅是无穷解中的一组，因此只需按一种策略进行验证即可，本文按先Wu(t)后Wv(t)策略进行。

5.1 机构结构参数

动平台与基座铰链点尺寸如图9所示。

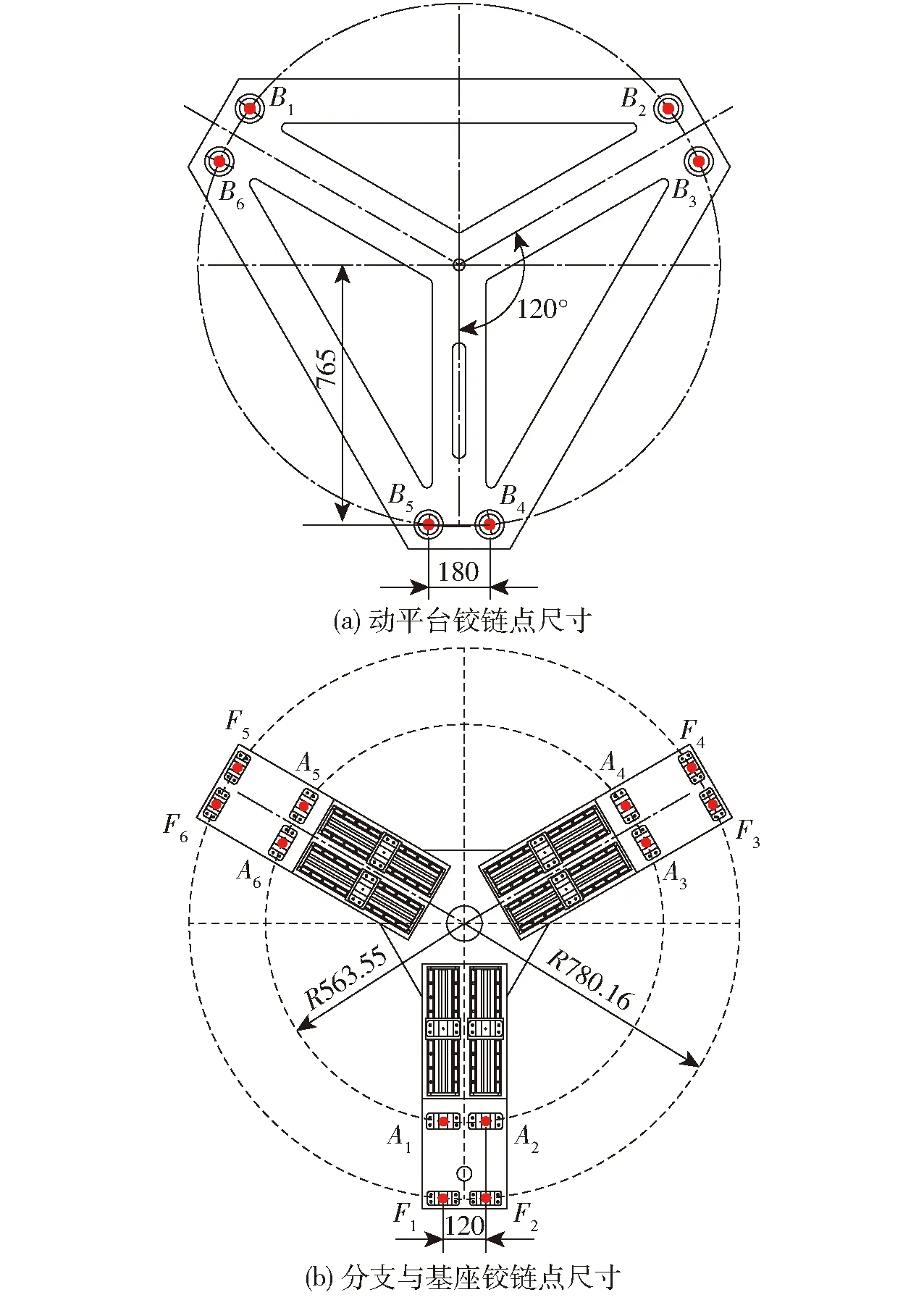
图9 铰链点分布尺寸图Fig.9 Distribution dimension diagram of hinge points

驱动分支内各杆件尺寸见表1。

根据上述参数建立机构三维模型，并导入ADAMS中进行运动学仿真。

表1 杆件尺寸参数

5.2 单自由度运动融合算例

首先验证机构在单一输出自由度方向上的运动融合能力，机构具有6个输出自由度，分别为3转动和3移动，任取其中2个单自由度运动作为数值算例。不失一般性，选取x轴方向转动和y轴方向转动为例。

(1)绕x轴方向转动

给定动平台单轴双模融合运动规律为

(23)

其中

rx(t)=r1x(t)+r2x(t)

(24)

式中rx——x轴角位移

r1x——x轴角位移位姿运动分量

r2x——x轴角位移振动分r1x(t)=10°sin(0.4πt)，r2x(t)=1°sin(2πt)，按先Wu(t)后Wv(t)规则，计算l1i(t)和l6i(t)的驱动增量u(t)和v(t)，理论值如图10所示。

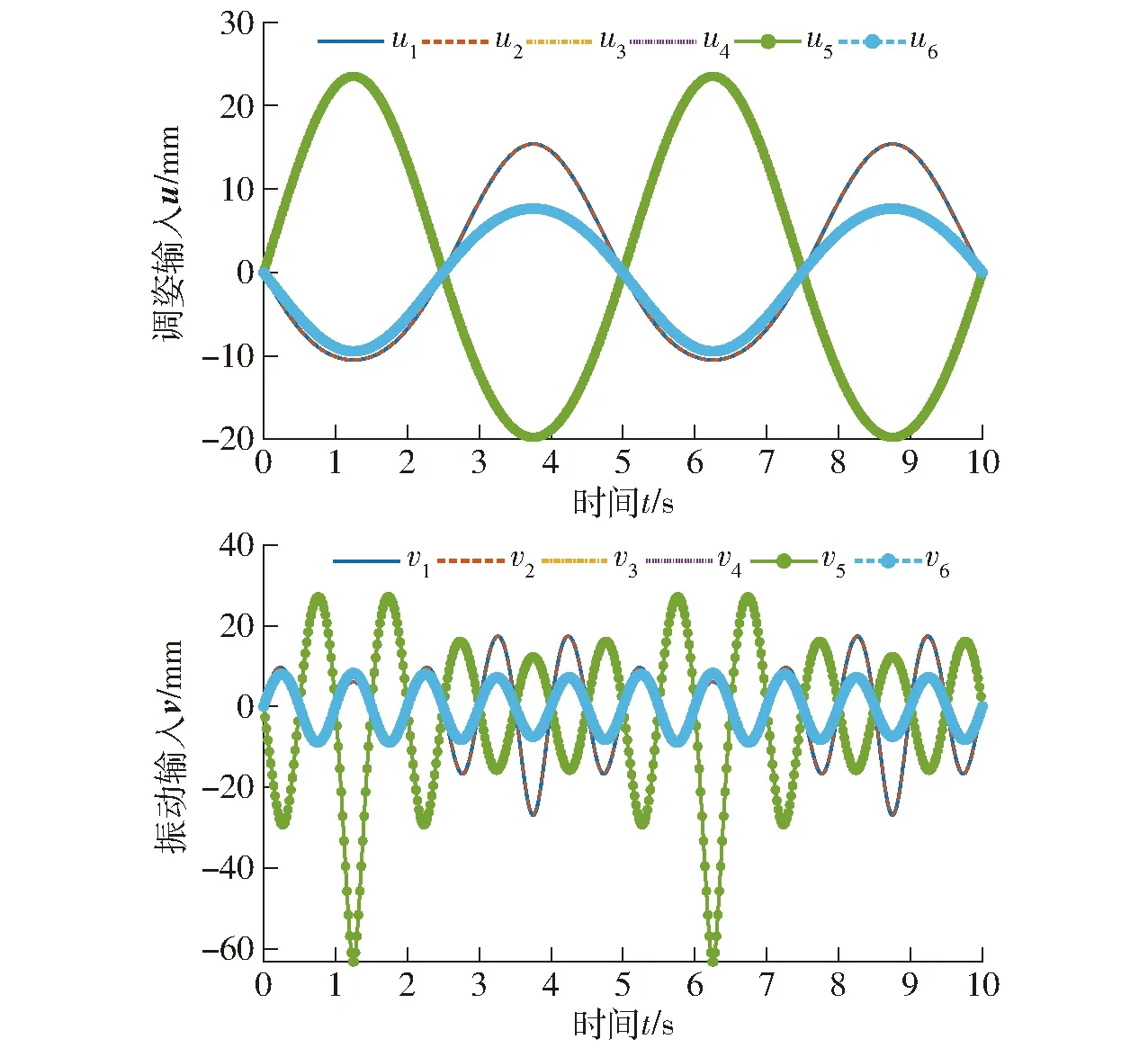
图10 绕x轴转动时双输入理论值Fig.10 Dual-input theoretical value of x-axis rotation

绕x轴转动时，容易判断分支1、2，分支3、6和分支4、5的驱动规律两两相同，因此图10中6条分支的驱动曲线两两覆盖，呈现3种规律。双模融合机构的运动学仿真需要通过2次仿真来验证。第1次，设定动平台运动规律为r1x(t)，并且令v(t)=0，仿真后测量u(t)的变化规律；第2次，设定动平台运动为r(t)，并将上一次仿真所得数据u(t)作为已知条件给入系统，仿真后测量v(t)。两次仿真得到的输入增量u(t)和v(t)的变化曲线如图11所示。

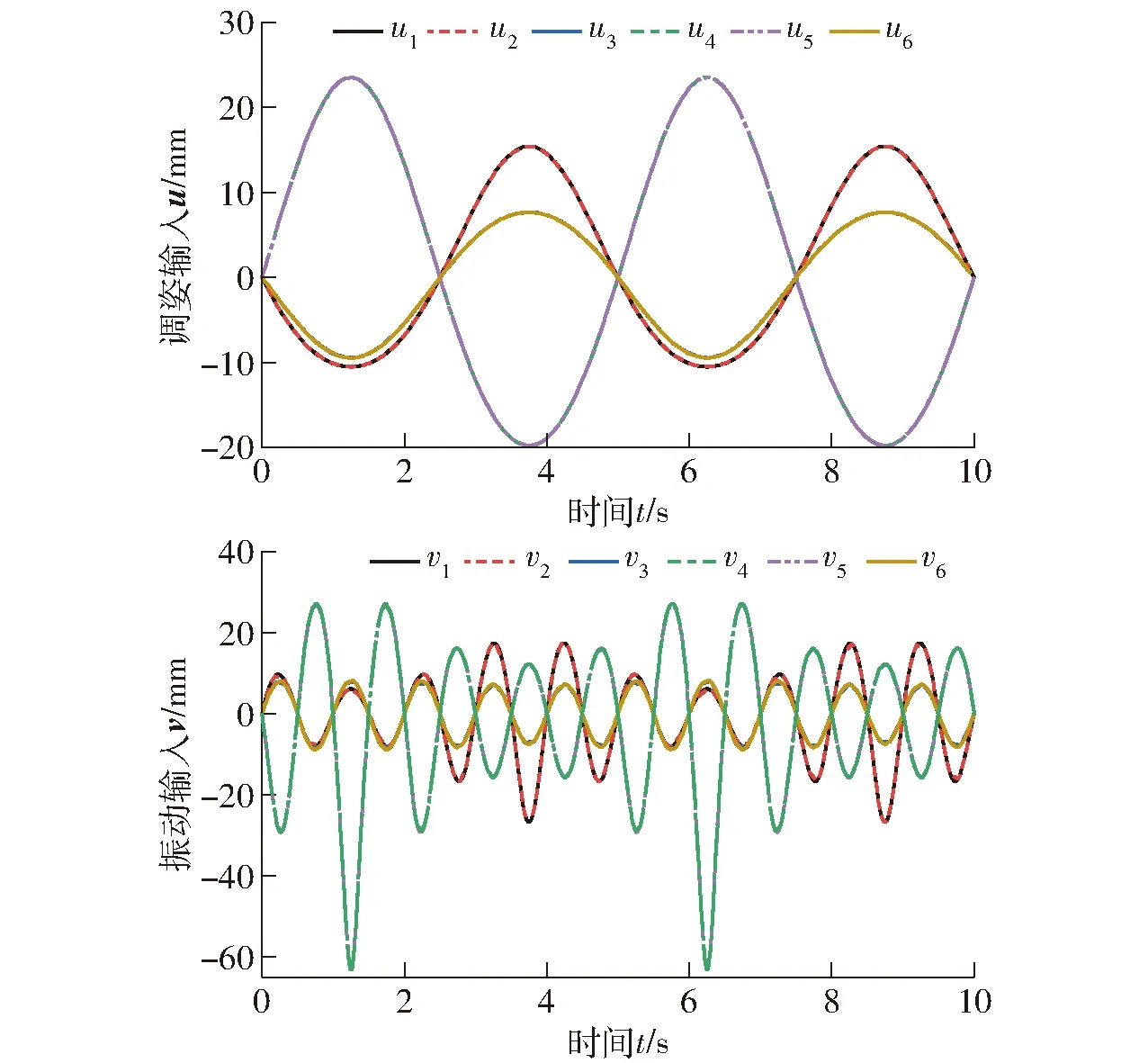
图11 绕x轴转动时双输入仿真值Fig.11 Dual-input simulation value of x-axis rotation

对比图10和图11可知，理论计算值与仿真值的变化趋势一致。进一步精确对比，将仿真数据导出并与每一时刻的理论计算值作差，得双输入偏差曲线，如图12所示。

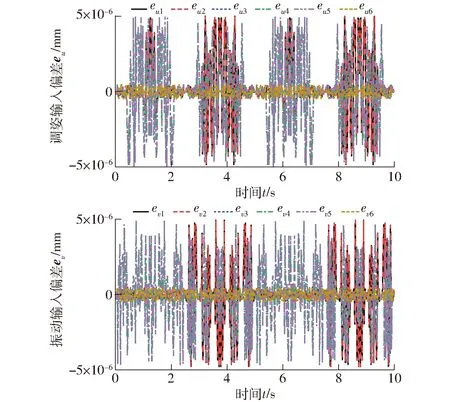
图12 绕x轴转动时理论与仿真输入偏差Fig.12 Input deviation between theory and simulation of x-axis rotation

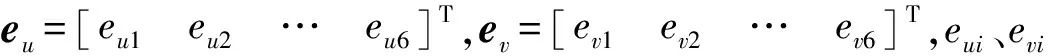
(2)绕y轴方向转动

给定绕y轴转动的双模融合运动规律为

(25)

其中

ry(t)=r1y(t)+r2y(t)

(26)

式中ry——y轴角位移

r1y——y轴角位移位姿运动分量

r2y——y轴角位移振动分r1y(t)=8°sin(2πt/3)，r2y(t)=0.5°sin(4πt)。同样按先Wu(t)后Wv(t)计算u(t)和v(t)的理论值，如图13所示。

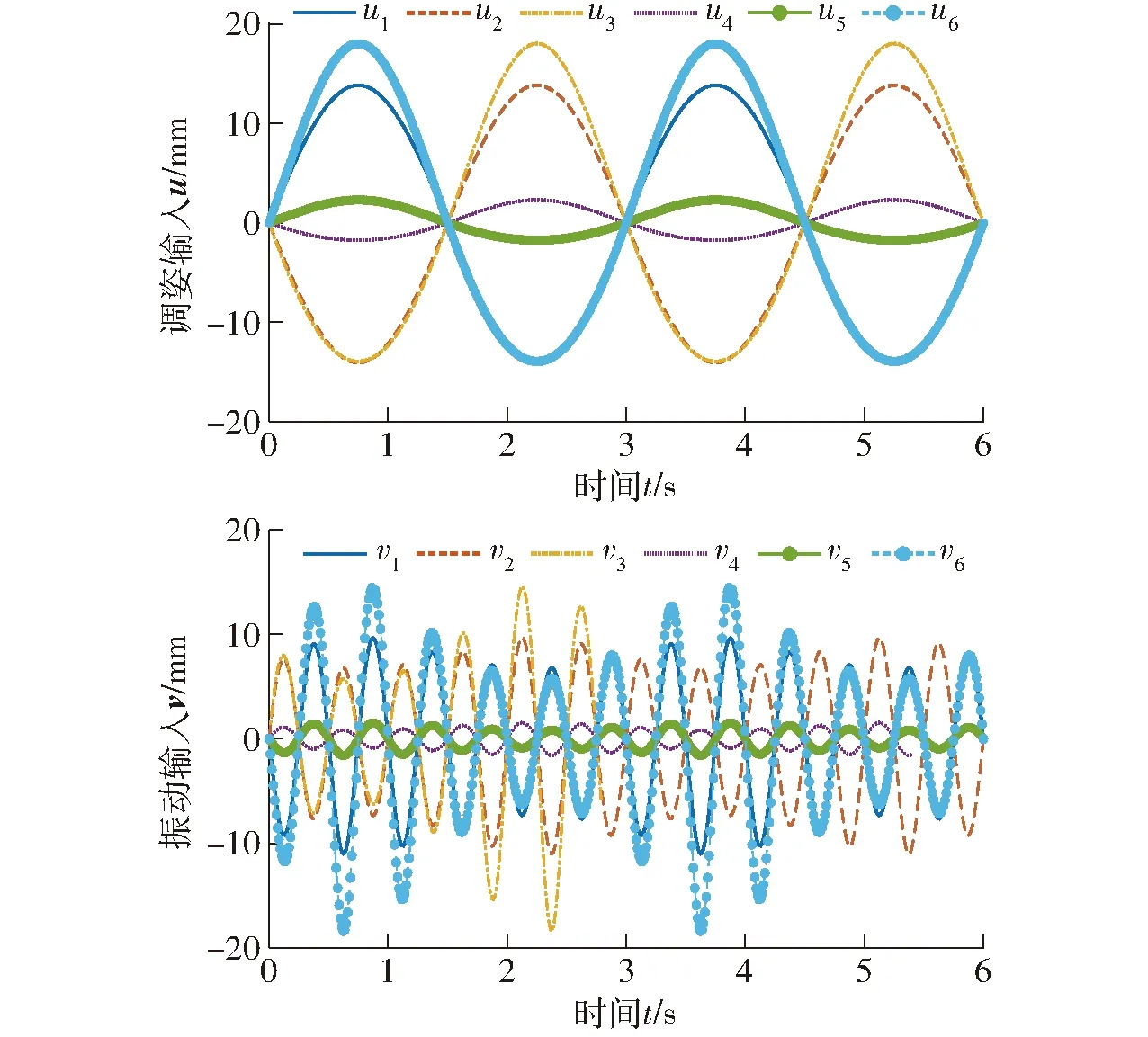
图13 绕y轴转动时双输入理论值Fig.13 Dual-input theoretical value of y-axis rotation

以相同运动规律在ADAMS中仿真，仿真同样需要两次，得仿真结果如图14所示。

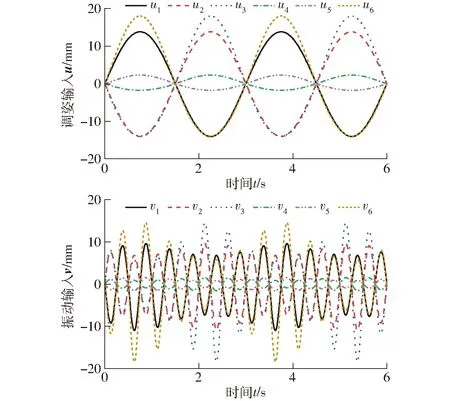
图14 绕y轴转动时双输入仿真值Fig.14 Dual-input simulation value of y-axis rotation

对比图13、14可知，理论计算与仿真结果曲线变化规律基本一致。进一步精确验证，同样作出理论计算与仿真结果的偏差曲线如图15所示。

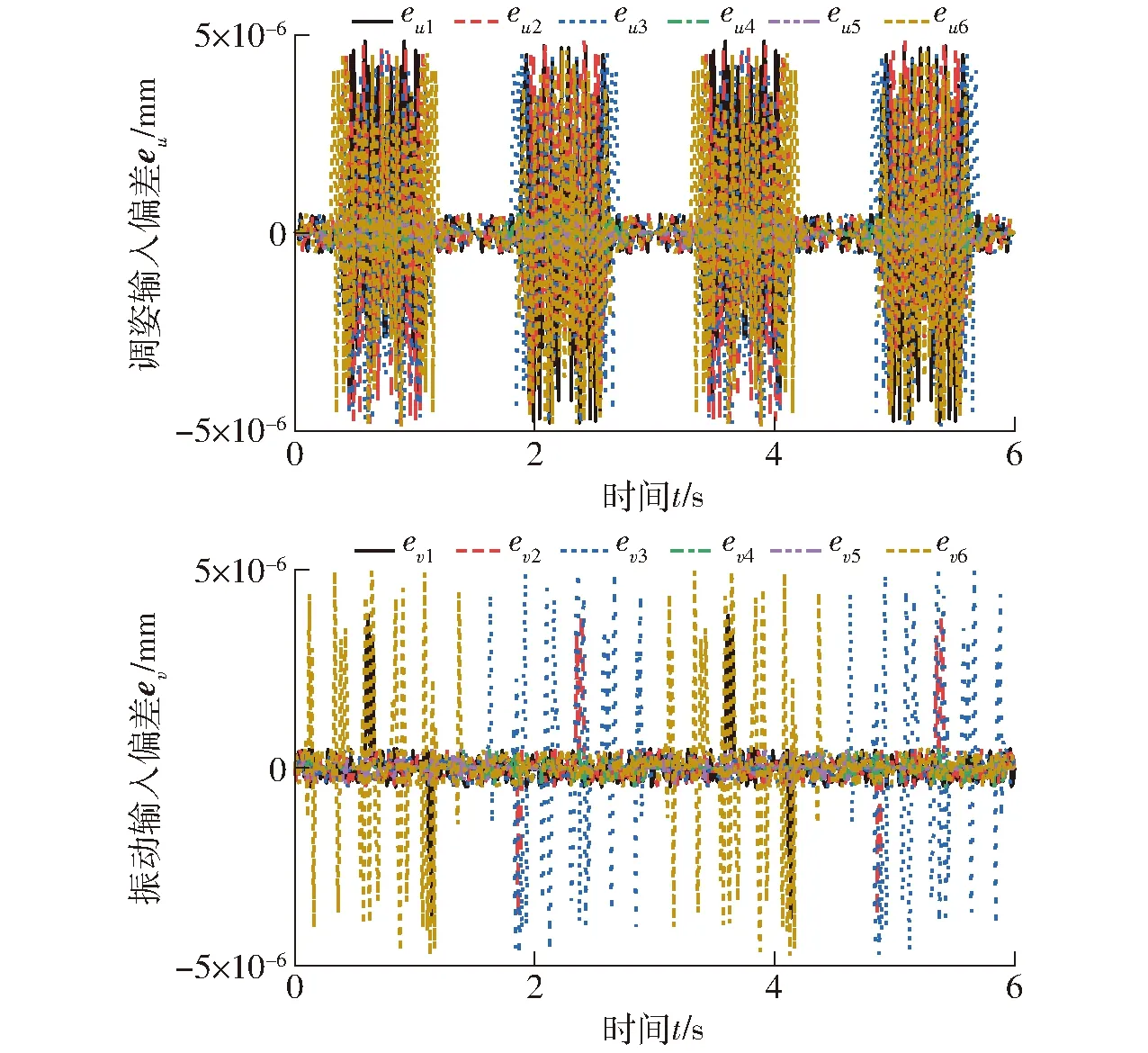
图15 绕y轴转动时理论与仿真输入偏差Fig.15 Input deviation between theory and simulation of y-axis rotation

图15中偏差数据同样为10-6量级，再次证明机构输出单自由度的融合运动时，理论值与仿真值完全一致。通过以上两个算例可以证明，机构反解的理论模型对于单自由度运动是正确的。

5.3 多自由度运动融合算例

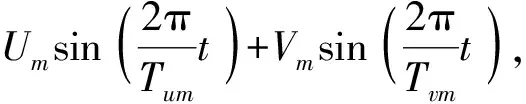
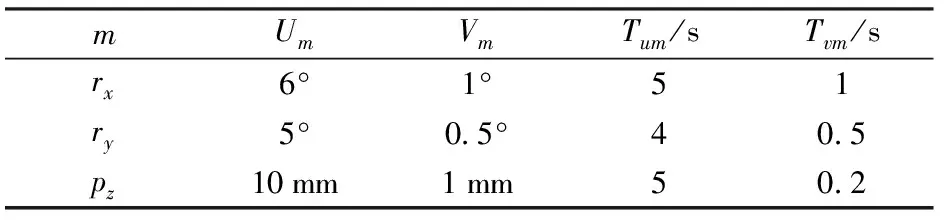
表2 融合运动参数Tab.2 Fusion motion parameters

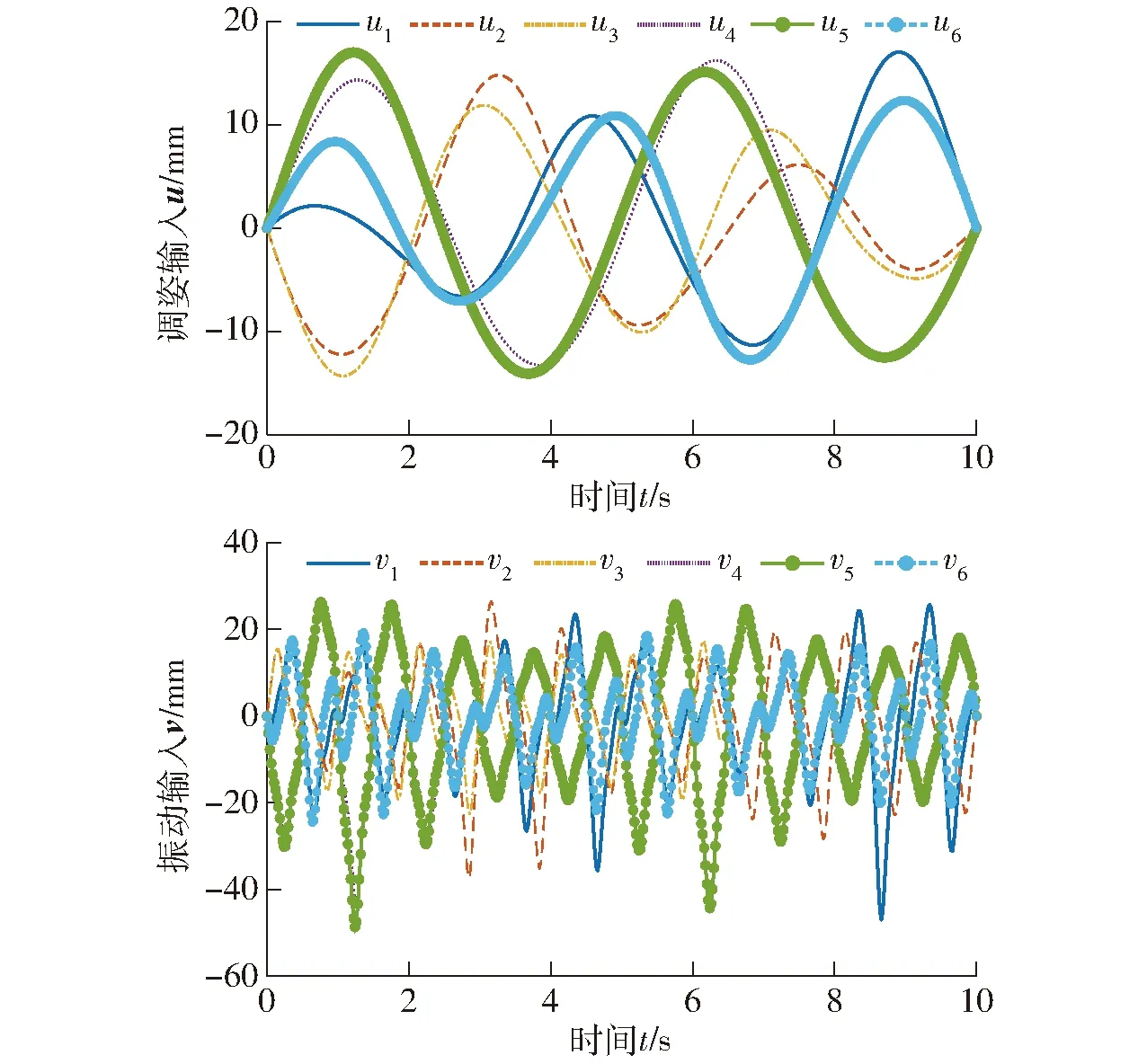
图16 三轴复合下双模融合运动输入理论值Fig.16 Theoretical values of inputs with dual-mode fusion motion under triaxial composite

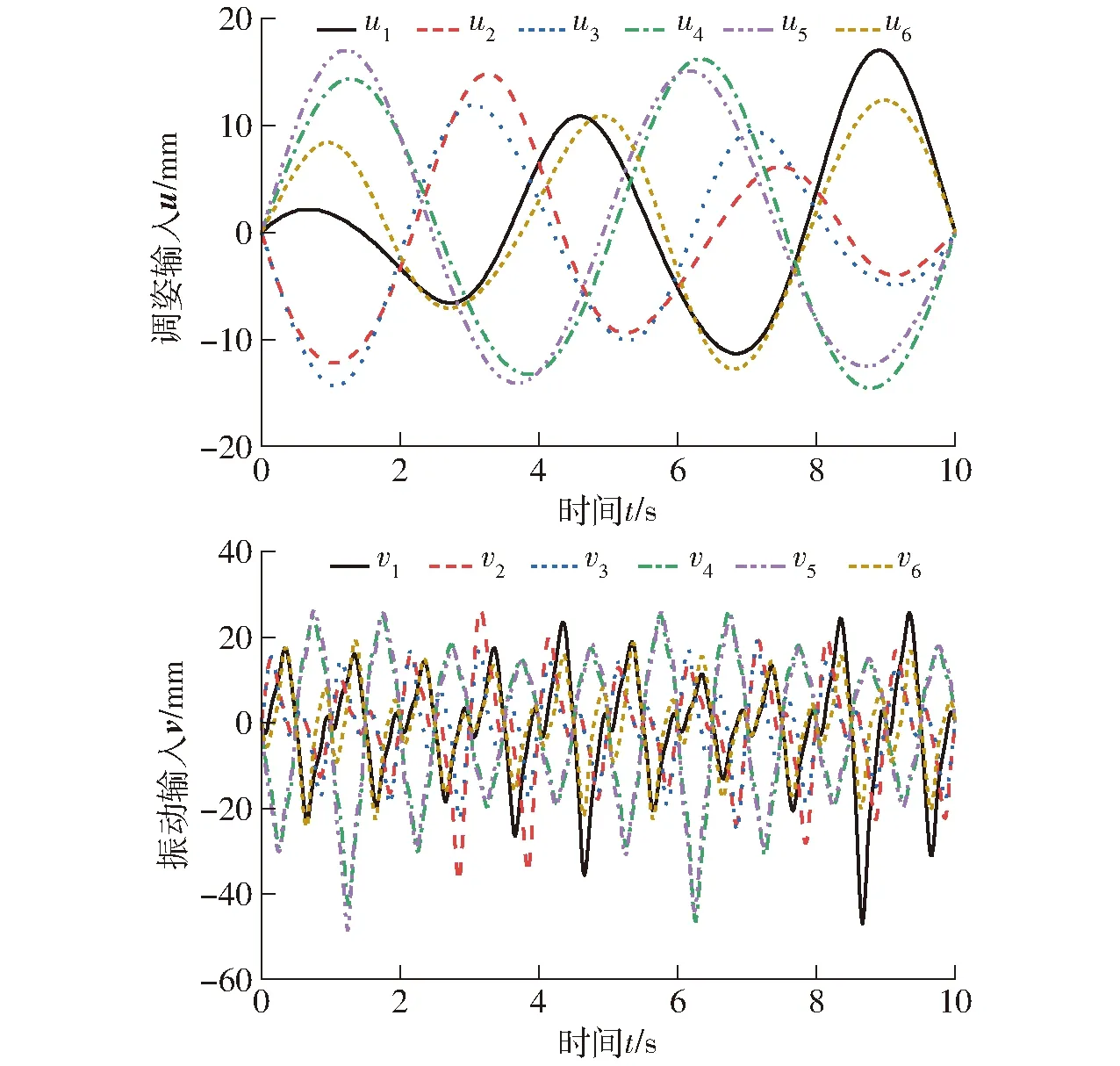
图17 三轴复合下双模融合运动输入仿真值Fig.17 Simulation values of inputs with dual-mode fusion motion under triaxial composite

根据给定的运动规律，并按先Wu(t)后Wv(t)规则，通过理论模型计算得双输入曲线如图16所示。以同样的运动规律和求解规则，运用ADAMS仿真得输入曲线如图17所示。计算、仿真过程与单自由度算例相似。

对比图16、17可知，三轴复合下，平台进行双模融合运动，输入理论计算值与仿真值变化趋势一致。导出理论值与仿真值数据，两者作差，并绘制偏差曲线如图18所示。

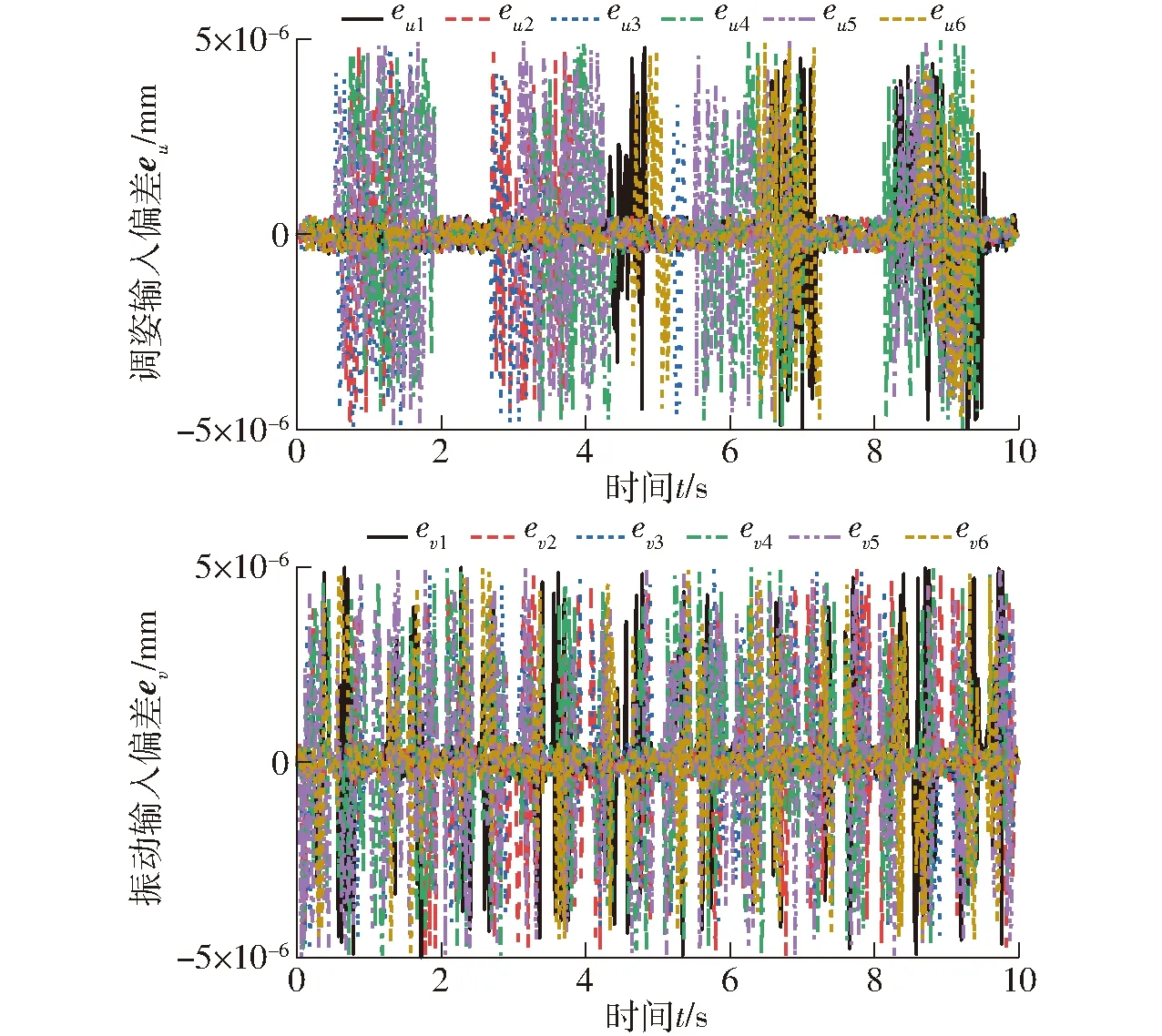
图18 三轴复合下双模融合运动输入偏差Fig.18 Input deviationof dual-mode fusion motion under triaxial composite

由图18可知，任意时刻理论计算与仿真结果的偏差均在10-6量级，可以认定理论结果与仿真结果完全相同。证明运动学反解理论模型对于多自由度复合下的双模融合运动同样正确。

5.4 运动学正解算例与仿真

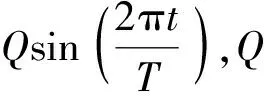
根据上述关系，任意给定一组各输入的幅值和周期，参数如表3、4所示。

表3 调姿输入参数Tab.3 Attitude adjustment input parameters

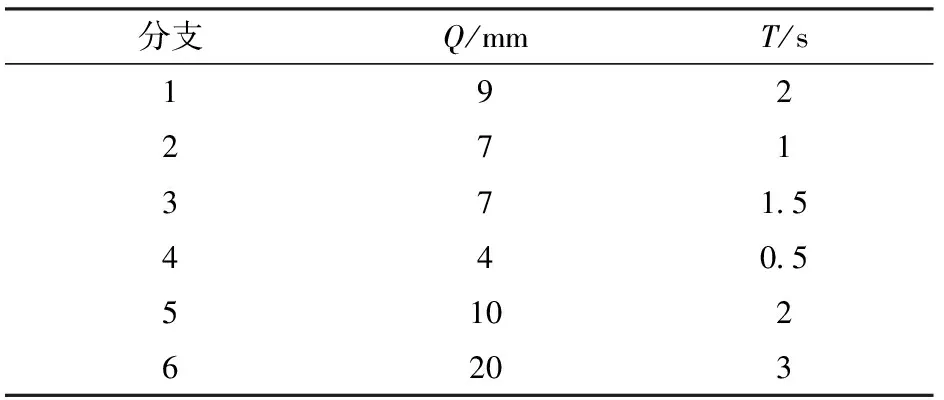
表4 振动输入参数Tab.4 Vibration input parameters

根据运动学正解的理论运算流程，在双输入融合驱动下，动平台的6维位姿输出曲线如图19所示，其中，rx、ry、rz为按x-y-z顺序欧拉角测量，rz为z轴角位移；px和py分别表示x轴位移和y轴位移。并将同样的驱动规律给入仿真模型，仿真后测量动平台的位姿输出，方位度量规则以及位置测量参考点与理论计算保持一致，测量结果如图20所示。

从图19、20可以看出，每个自由度上的运动均呈现大幅值上叠加小幅值的规律，证明机构能够把双输入子闭环内的两个独立的输入进行融合，并在输出运动上得以体现。对比理论结果和仿真结果，可以看出，动平台输出运动的规律是一致的。进一步精确对比，将仿真结果导出，并与理论计算值作差，得到正解位姿输出的偏差曲线如图21所示。

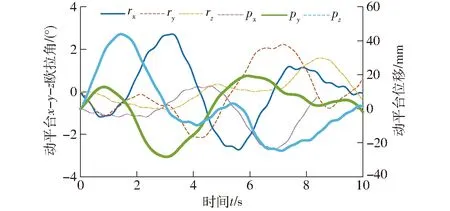
图19 动平台位姿理论值Fig.19 Theoretical posture of moving platform

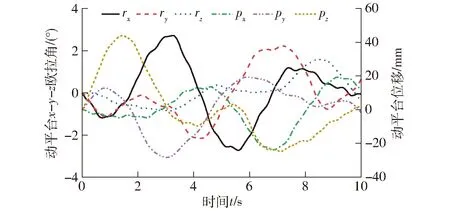
图20 动平台位姿仿真值Fig.20 Simulation posture of moving platform

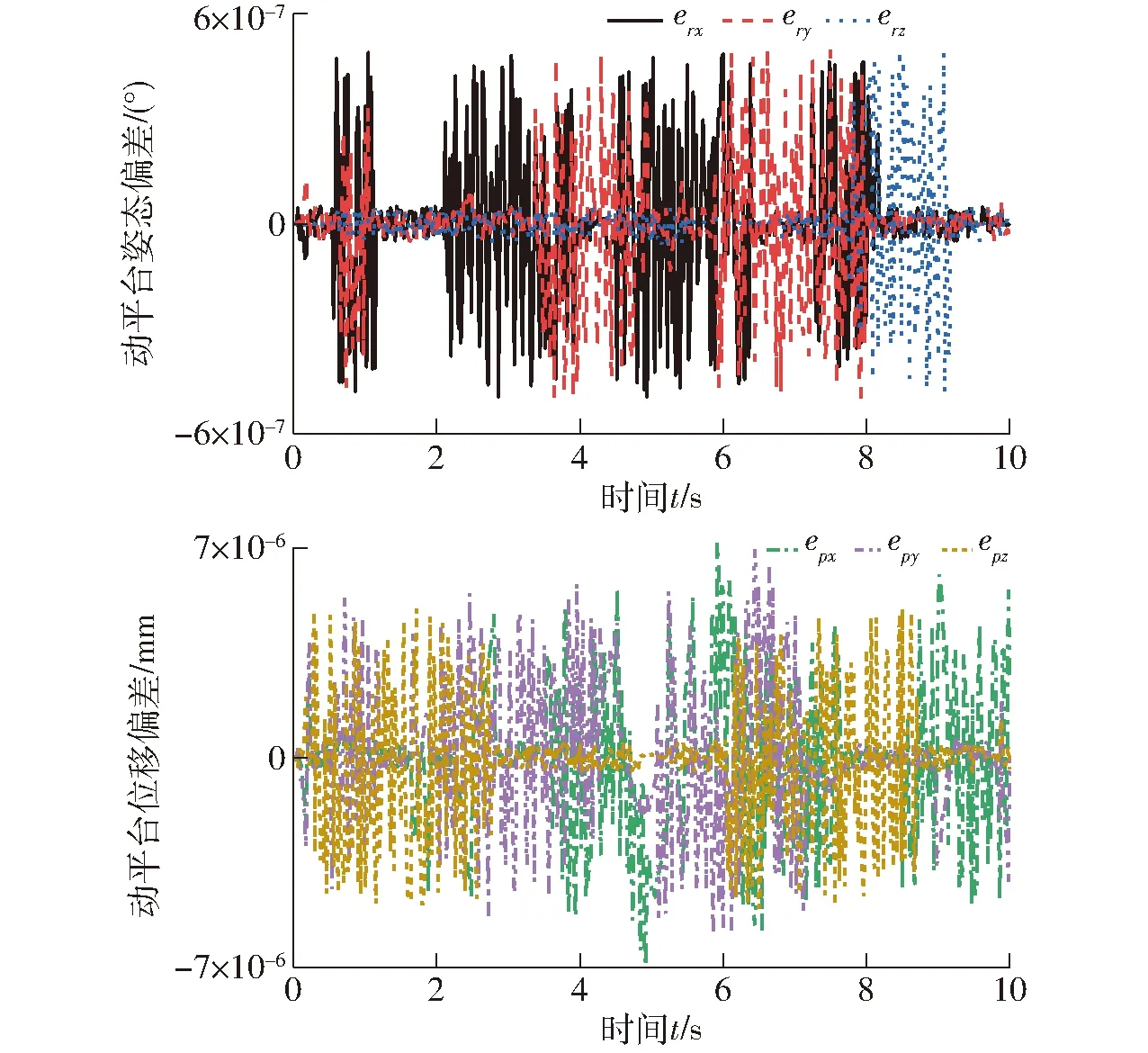
图21 理论值与仿真值位姿偏差Fig.21 Deviation of posture between theory and simulation

图21中，erx、ery、erz分别表示欧拉角3个方向的偏差，epx、epy、epz表示3个方向位移的偏差。由图21可知，偏差最大取值范围仍在10-6量级，可以认定理论结果与仿真结果完全一致。证明机构正解的流程与方法同样正确。

6 结论

(1)提出一种通过六杆机构与机构原驱动杆件组合的新型双输入子闭环结构。使机构既能实现双模式运动融合，又可以保持原6-RUS机构的原动件不变。

(2)建立机构运动学反解模型和内、外层机构数值方法的正解流程，将分析过程分为子闭环内与外主体机构两部分，子闭环的输出运动即为外主体机构的输入，其中外主体即为6-RUS机构，可以直接运用原有结论进行分析，将双输入融合的难点问题集中在双输入子闭环内。

(3)通过算例分别对单轴运动双模融合、多轴复合运动双模融合的反解，以及双输入融合驱动下的正向运动学进行理论计算与仿真验证，结果表明，理论分析结果与仿真结果完全一致，证明了针对所提构型所建立的运动学分析模型以及计算流程的正确性。