公司特征是否和收益率成非线性关系？

魏杰　文欣玥

摘   要：资产定价领域已成为金融学研究的热点。与传统因子模型不同，本文提出了加权非线性因子模型，将公司特征的未知函数作为因子载荷，时变的因子收益作为权重，研究股票超额收益率与公司特征之间是否存在非线性关系，以及模型对我国股票市场的适用性和解释力度。选取1995年7月—2020年6月我国A股上市公司的财务数据，考虑公司规模特征、价值特征和动量特征，采用核函数回归方法同时估计出因子载荷和因子收益，结果发现三个特征都是显著的，并且动量特征与收益率成非线性关系。此外，与美国股票市场相比，本文模型更加适用于中国股票市场，解释力度更强;与Fama-French三因子模型相比，本文估计误差更小。本文提出的模型在基本面分析和因子投资策略领域中具有借鉴意义。

关键词：股票市场;加权非线性因子模型;非参估计;资产定价

中图分类号：F830.91  文献标识码：B  文章编号：1674-2265（2022）05-0080-09

DOI：10.19647/j.cnki.37-1462/f.2022.05.011

一、引言

在我国金融市场中，股票超额收益率的决定因素一直是资产定价领域研究的热点。最为大众所接受的是Fama和French（1993）[1]提出的三因子模型（以下简称FF三因子模型），他们通过构建投资组合研究了公司特征与横截面收益率之间的线性关系，而本文利用非参数估计方法，将公司特征的函数作为因子载荷进行估计，研究公司特征与股票收益率之间的非线性关系。目前，国内文献鲜少运用非参数估计方法，资产定价方向的研究主要分为两类：第一类是通过增加新的因子，构建投资组合，研究流动性风险、投资者情绪、公司治理、全要素生产率对收益率的影响（宋光辉等，2017;齐岳等，2020;张少华和陈慧玲，2021;李双琦等，2021;周学伟等，2020）[2-6];第二类是采用机器学习方法研究多因子选股对交易策略的影响（干伟明，2018;周亮，2021）[7，8]。

资产定价模型的解释力度在不同国家存在差异，田利辉和王冠英（2014）[9]发现我国和美国金融市场的定价因子具有较大差异。Connor等（2012）[10]提出非参因子模型同时估计公司特征函数和因子收益，这种模型在中国股市的适用性也有待验证。

本文以1995年7月—2020年6月的中国股市收益率月度数据为样本，根据公司市值和账面市值比特征构建资产定价模型，其中，将公司特征形成的未知函数作为因子模型中的因子载荷，采用非参估计核函数回归方法，同时估计出特征函数和因子收益，回归结果显著，证明了股票收益率和公司特征之间确实存在非线性关系。此外，本文还和美国股市进行对比，实证结果发现本文构建的模型对中国股市的解释力度更大、误差更小。本文提出的模型适用于公司特征数较多、无法构建投资组合及高维面板数据的情况。

本文的主要贡献在于：第一，研究范围更广。传统因子模型采用排序方式进行分组，只研究了变量间的线性关系。而本文提出的加权非线性因子模型包括传统因子模型的研究范围，把因子载荷看作公司特征的未知函数，函数形式可以是任意的。第二，更符合实际情况。传统因子模型假设因子载荷是已知的，在组内是不变的，根据因子载荷估计因子收益。而本文模型中因子载荷是未知的，也需要估计。第三，本文模型可以解决维度诅咒问题，当传统因子模型出现高维数据时，由于构建投资组合个数有限，过高的维度会导致参数无法估计。本文通过对高维数据进行迭代估计，从而实现降维，可以研究连续变量。第四，本文对传统的三因子模型进行深入探讨，丰富了我国股票超额收益和公司特征存在非线性关系方面的研究。由于我国金融市场还不是有效市场，本文研究发现公司特征对超额收益有非线性影响，可以为基本面分析中国股市的超额收益提供依据。此外，最近较流行的多因子投资策略也是通过分析各种因子实现套利，所以本文提出的因子模型可以作为参考。

二、文献综述

古今中外，关于资产定价模型理论研究的文献非常多，从单因子模型发展到八因子模型。Sharpe（1964）[11]、Lintner（1965a;1965b）[12，13]等提出的模型是最早的单因子模型，用以研究资产收益率和市场系统性风险的关系。但是他们没有考虑规模效应和价值效应。于是，Fama和French（1993）[1]提出FF三因子模型，研究市场、规模、价值因子对股票超额收益率的影响。后来，学者们又引入动量因子（Carhart，1997）[14]、流动性因子（Pastor和Stambaugh，2003）[15]构建四因子模型，而Novy-Marx（2013）[16]把四因子模型中的规模因子换成盈利因子进行研究。Fama和 French（2015;2016）[17，18]在FF三因子模型基础上引入公司的盈利和投资因子，发现价值因子是“冗余”变量。Hou等（2015a;2015b）[19，20]則提出新的考虑规模、投资、盈利因子的资产定价模型。六因子和八因子模型也相继被提出，发现模型可以提高解释力（Barillas和Shanken，2018; Skočir和Loncarski，2018）[21，22]。最近几年，用资产定价模型来研究我国股票市场的文献也逐渐增加，主要集中在资产定价模型对比、模型的实证检验以及多因子选股策略等领域。赵胜民等（2016）[23]发现FF三因子模型比五因子模型更适合我国股市。李志冰等（2017）[24]检验了Fama-French五因子模型在我国股权分置改革前后的因子显著性。Liu等（2019）[25]提出了适合中国的价值因子、规模因子来解释股市的异象，如用净利润与市价比代替账面市值比。但他们都只研究了因子和超额收益率的线性关系，没有扩展到一般情况，未关注公司特征的函数与收益率之间的非线性关系。

国外学者认为因子和资产回报率之间可能存在非线性的关系，于是提出了非线性因子模型。Connor和Linton（2007）[26]改进因子模型的估计方法，把公司特征的函数作为因子载荷，进行非参核回归，同时估计特征函数和因子收益，以核函数为权重，通过格点将规模特征和价值特征对应在一定区间内，构建模仿FF三因子的投资组合，证明了因子收益的估计量比其更有效。但是这种构建投资组合的方法只考虑了离散变量的情况，不能解决因子面临的维度诅咒问题。他们进一步完善估计方法，放松限制，考虑在高维面板数据下，在连续变量存在时变情况下同时估计因子收益和因子特征函数（Connor和Linton，2012）[10]。这种非参估计方法比线性回归和构建组合方法的适用范围更广，不用构建投资组合，不用考虑因子个数，适用所有情况，还能解决维度诅咒问题。

近年来，国外学者深入研究基于公司特征的因子模型，发现公司特征对超额收益率影响很大。Freyberger等（2020）[27]利用LASSO方法筛选出公司特征，用非参估计方法研究这些特征如何影响预期收益，提供增量信息，从而提高预测精度。Raponi等（2020）[28]研究估计预期收益时贝塔资产定价模型的有效性，假设特征和因子载荷在不同资产间具有完全异质性而且允许在横截面上是任意相关的，发现公司特征的解释力比因子载荷更强。

通过文献回顾发现，国外文献较多采用非参估计方法进行研究，而国内文献以传统资产定价模型的实证检验和策略应用为主，形成了丰富的研究成果。但是，很少有学者将国内外研究结合起来，考虑股票收益率和公司特征之间存在非线性关系，将非参估计方法应用到我国股市的资产定价模型上。因此，在我国快速发展的金融市场中，研究非线性因子模型的解释力度具有一定的理论和现实意义。

三、模型构建

（一）模型设定

传统的资产定价模型采用的贝塔因子模型如下：

其中，[Rit]是个股[i]在时间[t]上的超额收益率，[αi]是截距，代表非系统风险为0时的资产收益率，[βiK]是第[i]个资产第[K]个因子的因子载荷，[fKt]是第[K]个因子在时间[t]的收益。

假设因子数据集与股票收益率之间存在非线性关系，即因子数据集形成的未知函数和股票收益率存在线性关系。所以，本文构建基于公司特征的因子模型来刻画股票市场的非线性现象。

其中，[rit]是第[i]个股票第[t]期的收益率;[rf]是无风险收益率;[fut]和[fjt]是因子收益;[Xij]是可观测的股票特征，假设不会随时间变化;[gjXij]是基于股票特征的未知函数，不会随时间变化，是模型估计的非参部分;[εit]是均值为0的股票收益率。因子特征函数[gjXij]可以把特征[Xij]映射到因子收益，所以因子收益[fjt]和因子特征函数[gjXij]相关。

我们可以看到，公式（2）是一种将基于特征的函数加权求和的一元因子模型，其中权重是因子收益[fjt]，会随时间变化，是时变参数。市场因子[fut]反映了和公司特征无關的资产共同收益的部分，所有资产的市场因子都有单位贝塔。它反映了所有股票共同移动的趋势，属于面板数据模型的共同因素。

（二）特征函数识别条件的提出

我们假设观测的特征都是独立同分布的，据此提出识别限制：对于每一个特征，特征函数横截面平均值为0，特征函数横截面的方差为1，即[E*gjXji=0，var*gjXji=1]。其中，[E*]是某个分布[P*]的期望，即[E*gj=gjxdP*jx]。选择不同的分布函数会影响特征的解释，[var*gjXij=1]这一条件设置了因子收益的大小，[E*gjXij=0]这一条件会影响对截距的解释。如果我们使用总体分布，则[E*gjXij=0]表示截距可以被解释为平均资产的收益;如果我们使用流通价值加权的总体分布，则[E*gjXij=0]表示截距是流通价值加权平均资产的收益。为了简化我们的理论，本文使用不加权总体分布。

四、方法对比

（一）构建投资组合回归法

我们先来回顾一下FF三因子模型方法。首先，把所有股票按照流通市值从小到大的顺序排列，前50%作为小市值（S）组，后50%作为大市值（B）组;用同样的方法，把所有股票按账面市值比分为三组，排名前30%的是低账面市值比（L）组，后30%的是高账面市值比（H）组，中间40%的是中间（M）组;从而构建SH、SM、SL、BH、BM、BL六大类投资组合，计算出规模因子（SMB）和价值因子（HML），而市场因子是市场所有股票的加权收益率与一个月国债收益率的差。其次，分别基于市值和账面市值比的大小将所有股票等分为五组，构建出25个投资组合，以流通市值作为权重，计算出加权的组合收益率。最后，以组合的超额收益率作为被解释变量，对市场因子、规模因子和价值因子进行最小二乘时间序列回归。

虽然通过构造投资组合方法可以解释哪些因素影响股票收益率，但是FF三因子模型还存在三点缺陷：第一，当因子个数较少时，可以通过有限的分类形成投资组合，但是当存在大量因子时，该方法不再可靠，无法通过构造多个投资组合来实现估计，这也正是本文需要解决的问题。第二，在估计因子载荷时，该模型没有考虑到动量因子等其他特征因子，误差项中可能存在和股票收益率相关性较高但未被解释的因子，可能会出现测量误差问题。第三，因子载荷的估计是在已知因子收益的前提下进行的，但是在现实中，因子收益和因子载荷都存在未知的可能性，需要同时估计出来。

（二）网格点估计法

Connor等（2007）[26]提出了新的构建组合方法迭。他们的模型采用格点法，每个数据对应一个目标特征向量的网格点。和FF三因子模型相比，他们计算投资组合收益率时采用核函数加权方法而不是流通市值加权平均法，并且根据每个资产的特征向量和目标向量的距离确定核函数的权重。

假设[J]个特征有[M]个不同的目标值，定义随机向量[X]集合中的元素[xmj]成为选中的值，所以目标特征向量的格点有[H=MJ]种组合，定义所有的目标向量组成的集合为[xh=xh1，xh2，…，xhJ′，h=1，2，…，H]，在给定[h]对应的向量[（m1，m2，…，mJ）]，每一个[xh]是[J]向量的目标特征值。从公司[i]中观察的特征值放入[Xi=Xi1，Xi2，…，XiJ′，i=1，2，…，n]。

其中，[rht]是加权投资组合收益率，[rit]是第[i]个股票第[t]期的收益率，[rht]是条件期望[rit]在[Ci=ch]下的非参估计量，[ωhi]是采用高斯核函数构建的核函数权重。

根据（5）式，构建基于核函数的投资组合收益如下：

对于每一个格点[xhj]，都有对应估计的因子特征值，由于[gj0=0]，[gj1=1]，所以[g1j=0]，[g2j=1]，他們对[M-2J]个因子特征函数g（.）和[J+1T]个因子收益进行估计，定义[θ=M-2J+J+1T]列向量参数矩阵，将公式（6）改写成非线性形式，得到：

其中，[δhj，m]是虚拟变量，当组合[h]有目标值[xmj]时，它就是1，否则就是0。

其中，加权矩阵[V]是对称正定矩阵，可以从数据中估计出来。[Qnθ]是四次多项式，有唯一合适的紧集。他们采用迭代加权最小二乘方法找到最小值[θ=gT，fTT]，使它满足：

Connor等（2007）[26]提出的估计方法可以同时估计因子特征函数和因子收益，得到的估计量是一致的且更有效。但是，此方法的缺点在于太过于依赖多元核函数方法创造投资组合，当遇到高维数据时，这些多元核函数会严重限制因子的个数，所以因子个数较多时，该方法变得不可靠。而本文提出的方法不需要多元核函数就可以进行估计。

（三）加权非线性因子模型非参估计

上述两个估计方法要求构建多个投资组合和多元核函数，估计的特征数目有限，而本文提出了一种新的估计策略，能快速估计出因子收益和因子特征函数，并且适用于多特征的情况。在非参估计部分，我们把问题分解成单独估计每个特征的子问题，子问题之间不断地迭代，最终得到估计结果，这是加权非参回归方法中的标准技巧。

我们先建立总体最小二乘标准：

只要满足上文提到的两个识别条件，就可以找到最小化的[QTf，g]了。

由于本文模型中[f]和[g]未知，都需要估计出来，而且最小化问题没有唯一解而是一组向量空间，所以我们采用无约束变量[gjxj]来替代[gjxj]。

其中，[P*jxj]是特征[j]的概率分布函数。

由于真实期望值无法得到，所以我们采用有界可调整的核函数回归估计量。我们估计条件期望[Eyit|Xij=x]如下：

比如，[Khx，y=Kxhx-y=h-1Kxh-1x，y]表示[x]在[Xij]内部支持。[K]是核函数，[h]是带宽。我们假设每个协变量在已知区间[[x，x]]里，协变量密度是非0有界的。我们需要对核函数做出有界调整确保误差在每个地方都是相同大小的。

当资产总体是固定的时候，最小化问题可以看作一系列线性回归问题，采用最小二乘法估计系数。但是当资产总体是随机的时候，我们先固定因子特征函数[g.]，分别对（11）式中的[fut]和[fjt]求一阶导，得到：

接着，我们再固定因子收益[fut]和[fjt]，采用Gateaux对（11）式在[ψ.]函数方向上求点导数。

我们通过不断迭代解决这一问题，共分为四步：

第一步是设置第一次迭代的初始值[f0]和[g0]，满足一致性;第二步是按照（18）式，根据[f0]估计第二次迭代的[g1]：

五、实证研究

（一）数据来源及说明

本文从国泰安数据库中选取了中国A股市场所有股票的个股收益率和公司财务报表等信息，研究区间是1995年7月—2020年6月，总共有300个月，样本量为382884。。因为A股市场于1995年才开始逐渐发展壮大，之前上市公司数量不够多，信息不够齐全，而且每年末的公司财务报表会在下一年的7月份之前全部披露完成，所以选择1995年7月作为样本区间起点。我们把1995年7月—1996年6月的数据看作1995年的年度数据，以此类推。对数据进行筛选和预处理，剔除掉流通市值排名后10%的公司。为了防止出现借壳上市的公司，不考虑上市时间小于6个月的公司、金融行业公司和ST股票。以流通市值加权平均法计算的考虑现金红利再投资的综合A股市场回报率作为市场收益率，以月度化定期整存整取一年的利率作为无风险利率，以考虑现金红利再投资的月度个股回报率作为股票收益率。使用市值账面比（流通市值与所有者权益的比值）作为价值特征，个股超额收益率是个股回报率减去无风险收益率，市场因子收益是市场收益率减去无风险收益率。为了方便研究，以上数据统一转化成月度数据。

以往文献研究发现，规模效应、价值效应、动量效应对股票横截面收益有重大影响。因此，构建基于公司规模、价值、动量特征的非线性因子模型：

其中，[rit]是个股收益率，[rf]是无风险收益率，市场因子[fut]反映了和公司特征无关的资产共同收益的一部分，G（.）表示基于公司特征的特征函数，[Size]是流通市值，[Value]是市值与账面价值的比，[Mom]是个股的前12个月收益率之和，[fit]代表因子收益。

（二）评价模型解释力度

本文评价模型解释力度的指标共有两个，分别是根均方误差（[RMSE]）和平均去中心化的[R2]统计量（[UR2]）。[RMSE]值越小，[UR2]值越大，则代表模型的解释力度越强。

其中，[yit]是真实的个股超额收益率，[yit]是模型估计出的拟合值。

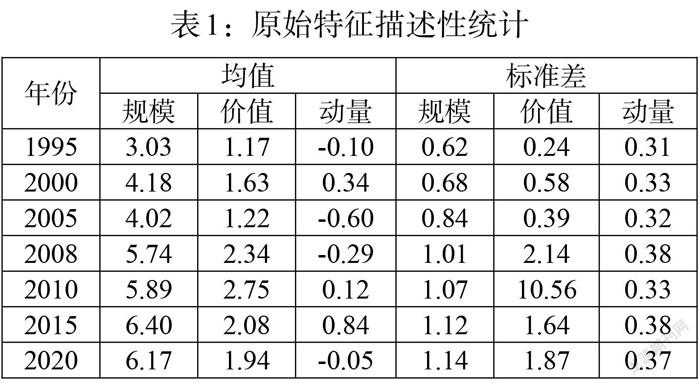
（三）描述性统计

本文对原始三个特征进行描述性统计（见表1）。由于篇幅限制，只列举每隔5年以及中间年的6月份的均值和标准差。结果发现，规模特征的均值最大，动量特征的标准差最小。

把每年的7月作为横截面，将3个公司特征两两匹配得到3组横截面之间的相关系数（见图1）。从图中可以看出，这3个特征之间的相关性都是从负数到正数持续震荡。平均来说，动量特征和规模特征成正相关，动量特征和价值特征成负相关，价值特征和规模特征成正相关。

六、模型效果

（一）估计结果

当解释变量是时变的，直接估计特征函数是不可行的。我们将因子载荷的估计集中在-3和3之间的61个等距网格点上，相邻网格点间隔0.1，使用线性插值法计算因子载荷，再根据资产收益率和因子载荷估计因子收益。由于因子载荷和格点是线性关系，这个过程可以提高算法速度。

选择高斯核进行非参估计条件期望，这种核的优点在于能够平滑地估计连续变量。设置格点的带宽等于样本密度的10%分位数，这就暗示了90%的观测值不在格点内。当带宽越窄时，数据更密集一些，反之，数据更稀疏一些。

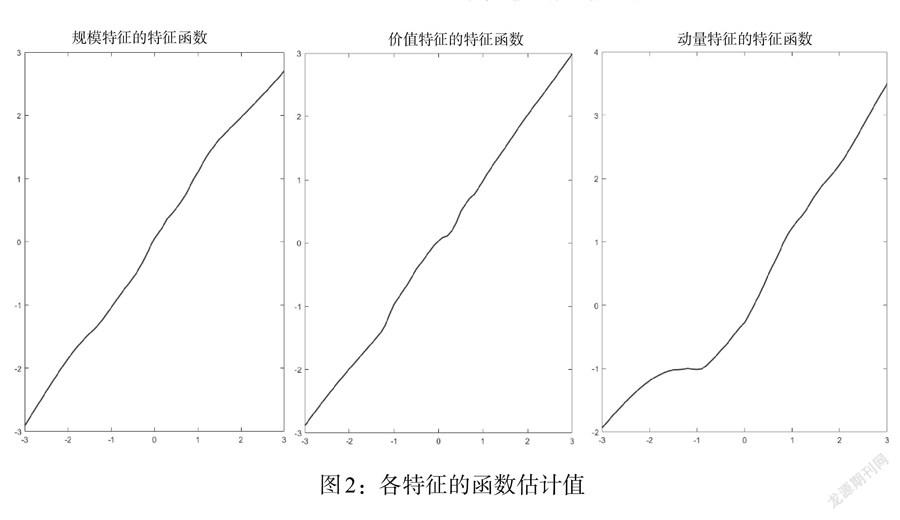
将估计出来的因子载荷进行标准化（见图2）。从图2可以看出，这3个特征函数都是单调递增的，规模特征、价值特征的函数接近于线性，而动量特征的曲线是非线性的。

（二）模型解释力度

在每一步迭代估计中，因子收益是前一个迭代因子特征函数的回归系数。为了衡量因子解释力，我们采用最后一步的特征函数估计值，并且对所有特征、单个特征、剩余特征进行横截面回归（见表2）。表2中第一行是只对当前的特征进行回归得到的[UR2]，第二行是剩余特征的[UR2]，最后一行是三个特征非线性回归得到的[UR2]。从表2中可以看到，市场因素在解释力上是主要的，其次是规模特征、动量特征和价值特征。

为了和Connor（2012）[10]研究美国股票市场的[UR2]进行对比，选择1995—2007年的中国股票市场作为观测區间，计算出[UR2]为35.97%，比美国股市[UR2]19.81%要大一些，说明本文提出的模型解释力度更强，更适用我国的股票市场。

我们通过计算横截面上估计系数的[t]统计量检验每个特征的显著性（见表3），发现在95%置信水平上，每个特征的显著月份的比重都超过50%，说明所有特征是显著的。

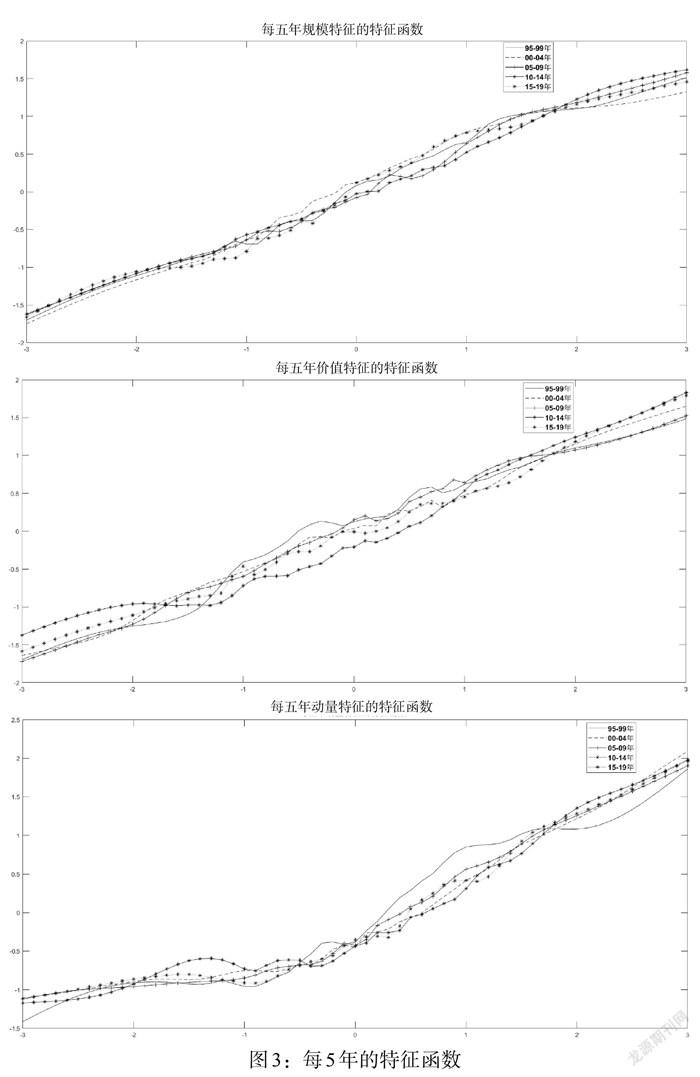
将25年数据拆分为5个5年估计区间，分别估计特征函数，并且进行标准化，如图3所示。结果发现这三个特征的每五年特征函数相差不是很大，大体保持在一条线上。说明本文估计的特征函数具有稳健性。

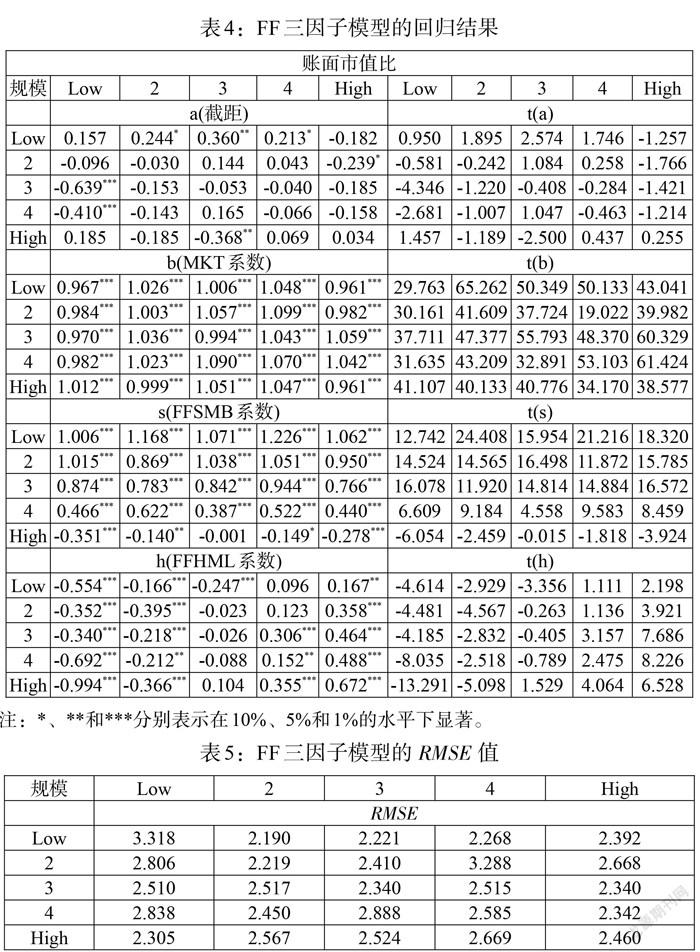
（三）与FF三因子模型对比

本文按照FF三因子模型，构建25个投资组合的加权平均收益率，计算规模因子和价值因子，进行回归（见表4）。结果发现所有投资组合中市场因子均显著，而在有些投资组合中规模因子和价值因子不显著。但是，本文构建的非线性因子模型中市场、规模和价值三个特征都显著，非线性因子模型[RMSE]值为0.324，比FF三因子模型的PMSE值小（见表5），说明本文提出的模型解释效果更好。

七、结论

本文提出一种新的估计方法，构建加权非线性因子模型，研究公司特征与股票收益率存在的非线性关系以及模型的解释力度，能有效解决维度诅咒问题，适用于公司特征数较多、无法构建投资组合及高维面板数据的情况，丰富了我国股票收益率和公司特征存在非线性关系方面的研究。

本文选取了1995年7月—2020年6月我国A股上市公司的财务数据，考虑公司规模特征、价值特征和动量特征，把这些特征的未知函数作为因子载荷，时变因子收益作为权重，采用格点法将特征函数映射到格点区间内，用高斯核估计条件期望，通过对高维数据不断迭代估计参数，从而实现降维，同时估计出特征函数和因子收益，得到回归结果。结果发现，特征函数满足识别条件，是单调递增的，其中动量特征和收益率是非线性关系。我们还通过计算模型的[UR2]研究了模型的解释力度，发现市场因素在解释股票收益率上占主要地位，其次是规模特征、动量特征和价值特征，回归结果中这三个特征是显著的。此外，本文还将中美两国股票市场进行对比，研究发现本文提出的模型更加适用于中国，解释力度更大;将本文的模型和FF三因子模型进行对比，发现FF三因子模型构建的所有投资组合中市场因子均显著，而在有些投资组合中规模因子和价值因子不显著，而且估计误差比本文模型更大，说明本文模型的解释效果比传统三因子模型更好。本文提出的非线性因子模型，有助于通过基本面分析研究我国股市的超额收益，也能为金融市场的多因子投资策略提供参考建议。

参考文献：

[1]Fama E F，French K R. 1993. Common Risk Factors in the Returns on Stocks and Bonds [J].Journal of Financial Economics，33.

[2]宋光辉，董永琦，陈杨炀，许林.中国股票市场流动性与动量效应——基于Fama-French五因子模型的进一步研究 [J].金融经济学研究，2017，（01）.

[3]齐岳，周艺丹，张雨.公司治理水平对股票资产定价的影响研究——基于扩展的Fama-French三因子模型实证分析 [J].工业技术经济，2020，（04）.

[4]张少华，陈慧玲.全要素生产率是有效的资本资产定价因子吗？——基于中国股市的Fama-French因子模型检验 [J].中国经济问题，2021，（02）.

[5]李双琦，陈其安，朱沙.考虑消费与投资者情绪的股票市场资产定价 [J].管理科学学报，2021，（04）.

[6]周学伟，付巾书，宋加山.不同的政策不确定性对股市波动影响相同吗？ [J].金融发展研究，2020，（05）.

[7]干伟明.基于多因子资产定价模型的A股市场配对交易策略研究 [J].金融理论探索，2018，（06）.

[8]周亮.基于随机森林模型的股票多因子投资研究 [J].金融理论与实践，2021，（07）.

[9]田利辉，王冠英.我国股票定价五因素模型：交易量如何影响股票收益率？ [J].南开经济研究，2014，（02）.

[10]Connor G，Hagmann M， Linton O. 2012. Efficient Semiparametric Estimation of the Fama-French Model and Extensions [J].Econometrica，80（2）.

[11]Sharpe W F. 1964. Capital Asset Prices：A Theory of Market Equilibrium under Conditions of Risk [J].The Journal of Finance，19（3）.

[12]Lintner J. 1965. The Valuation of Risk Assets and the Selection of Risky Investments in Stock Portfolios and Capital Budgets [J].Review of Economics and Statistics，47（1）.

[13]Lintner J. 1965. Security Prices，Risk，and Maximal Gains from Diversification [J].The Journal of Finance，20（4）.

[14]Carhart M M. 1997. On Persistence in Mutual Fund Performance [J].The Journal of finance，52（1）.

[15]Pastor L，Stambaugh R F. 2003. Liquidity Risk and Expected Stock Returns [J].Journal of Political Economy，111（3）.

[16]Novy-Marx R. 2013. The Other Side of Value：The Gross Profitability Premium [J].Journal of Financial Economics，108（1）.

[17]Fama E F，French K R. 2015. A Five-Factor Asset Pricing Model [J].Journal of Financial Economics，116（1）.

[18]Fama E F，French K R. 2016. Dissecting Anomalies with a Five-Factor Model [J].The Review of Financial Studies，29（1）.

[19]Hou K，Xue C，Zhang L. 2015. Digesting Anomalies：An Investment Approach [J].The Review of Financial Studies，28（3）.

[20]Hou K，Xue C，Zhang L. 2015. A Comparison of New Factor Models [W].Working Paper Series，Ohio State University，Charles A. Dice Center for Research in Financial Economics，05.

[21]Barillas F，Shanken J. 2018. Comparing Asset Pricing Models [J].The Journal of Finance，73（2）.

[22]Skočir M，Loncarski I. 2018. Multi-Factor Asset Pricing Models：Factor Construction Choices and the Revisit of Pricing Factors [J].Journal of International Financial Markets，Institutions and Money，55.

[23]趙胜民，闫红蕾，张凯.Fama-French五因子模型比三因子模型更胜一筹吗——来自中国 A 股市场的经验证据 [J].南开经济研究，2016，（02）.

[24]李志冰，杨光艺，冯永昌，景亮.Fama-French五因子模型在中国股票市场的实证检验 [J].金融研究，2017，（06）.

[25]Liu J，Stambaugh R F，Yuan Y. 2019. Size and Value in China [J].Journal of Financial Economics，134（1）.

[26]Connor G，Linton O. 2007. Semiparametric Estimation of a Characteristic-Based Factor Model of Common Stock Returns [J].Journal of Empirical Finance，14（5）.

[27]Freyberger J，Neuhierl A，Weber M. 2020. Dissecting Characteristics Nonparametrically [J].The Review of Financial Studies，33（5）.

[28]Raponi V，Robotti C，Zaffaroni P. 2020. Testing Beta-Pricing Models Using Large Cross-Sections [J].The Review of Financial Studies，33（6）.

Are Company Characteristics and Stock Return in a Non-linear Relationship？

——Based on the Empirical Research of Chinese Stock Market

Wei Jie/Wen Xinyue

（School of Economics，Huazhong University of Science and Technology，Wuhan   430000，Hubei，China）

Abstract：Asset pricing has been overwhelmingly researched in finance. A weighted nonlinear factor model is established based on existing research results，with unknown functions of firm characteristics as factor loadings and time-varying factor returns as weights，to investigate whether there is a nonlinear relationship between stock excess returns and firm characteristics，and the applicability and explanatory strength of the model to China's stock market. The financial data of China's A-share listed companies from July 1995 to June 2020 are selected，and the characteristic functions and factor returns are estimated simultaneously by using kernel function regression method considering firm size characteristics，value characteristics and momentum characteristics，and it is found that all three characteristics are significant and the momentum characteristics are nonlinearly related to the returns. In addition，the model in this paper is more applicable to the Chinese stock market and has stronger explanatory power compared to the US stock market; compared with the Fama-French three-factor model，the estimation error in this paper is smaller. The model proposed in this paper has implications in the field of fundamental analysis and factor investment strategies.

Key Words：stock market，weighted nonlinear factor model，nonparametric estimation，asset pricing

（责任编辑    关   健;校对   LY，WY）

收稿日期：2021-12-09      修回日期：2022-01-21

作者简介：魏杰，男，华中科技大学经济学院副教授，研究方向为微观计量经济学、因子模型;文欣玥（通讯作者），女，华中科技大学经济學院，研究方向为资产定价。