基于高斯模型的船舶航行避险航线设计研究

李成海，赵卫健，胡甚平

（1. 山东交通职业学院 航海学院， 山东 潍坊 261206；2. 上海海事大学 商船学院， 上海 201306）

0 引言

船舶航行可能会遭遇狂风巨浪等季节性外部环境，从而引发船舶航行事故性高风险事故，还可能经过船舶密度大且作业渔船多等特定水域，引发船舶航行风险事故。船公司力求避免上述两种事故的意外发生，因而制定规避风险海区的航行路线成为必然。但是，航运公司追求航运利润最大化的目的决定了船公司不可能无限制地舍弃航运收益为规避风险而绕航，所以在综合考虑了船舶航行决策者风险偏好不同的前提下，选取船舶航行最佳避险航线显得非常重要。

关于船舶航线设计问题，相关学者做了大量研究，例如戴厚兴采用模糊评判法构建大风浪环境下海上交通风险评估模型，重点模拟外部环境和重点船舶，提高了评估风险的科学性和合理性。[1]吴恭兴等通过改进A*算法函数，将大风浪引发的船舶失速因素加入航线代价值计算中，从而设计一条避开恶劣海区的航线。[2]石浩等提出基于船舶自动识别系统数据和区域栅格化构建航行模型，运用蚁群算法解算最优航线的设计方法，通过在中国沿海实例验证表明该方法在最优航线设计方面具有经济和安全的效果。[3]李晓岩在构建航线设计数学模型前，对路线设计进行描述，并设定目标函数，根据选定函数作蓝本，使用约束处理结果对设计航线进行分析，获取最优计划航线。[4]刘亮龙提出新的船舶航线数据挖掘方法，将数据分成静态、动态、航行资料及安全信息，选取D-P 算法压缩数据，从而快速挖掘数据。[5]吴向峰提出基于多元船舶航线校正方法，首先校正航线数据的预判计算，根据预判计算数据构建航线校正的动态模型，将模型修正量数据导入修正算法中，实现对航线数据的动态校正，对比实验表明该方法具有较强的可行性。[6]

高斯模型，Dabrowski 将其应用于海上搜救路径研究，作为基于地理信息环境中基本功能被多领域应用。[7]但时至今日，仍没有学者将高斯模型与航线设计结合的研究。本研究将两者结合起来，考虑到航行船舶航线规避风险的要求，并根据当时当地的船舶航行决策者不同偏好，为航行船舶设计避险航线。

1 避险航线描述

船舶海上航行避险航线设计问题，实质上是一种安全和低成本规划设计问题。在规划设计中，预设计划航线海区船舶航行事故性风险与船舶航行风险的年事故统计，船舶出发港和目的港船舶偏好航线，求解一条综合考虑了船舶偏好且相对风险小的航线。采用考虑了预规划设计海区环境条件和起始港限制条件下的，以航线的整体风险成本值最小为目的的数学函数计算结果值的避险航线。如下是描述综合考虑了船舶偏好的避险航线设计过程中所涉及的参数和集合。

A =（a1，a2，…，an），根据历年海上事故统计出的该海区一段时间内的n 次发生事故性高风险的集合，其中 ai表示第 i 次发生事故性高风险，i = 1，2，…，n。

B =（b1，b2，…，bm），根据历年海上事故统计出的该海区一段时间内的m 次发生风险的集合，其中bj表示第 j 次发生事故性高风险，j = 1，2，…，m。

综合分析船舶偏好相对风险小的航线设计问题，是在掌握航经海区风险分布情况前提下，依据航线所经海区风险分布不同及船舶偏好预设计的相对安全航线。[8]本研究需解决如下问题：识别船舶航经海区风险分布情况，根据海区风险分布差异，综合考虑不同船型船舶偏好区别，计算得出相对安全海上航线。

2 构建综合考虑偏好的船舶海上航线设计模型

2.1 船舶海上航行风险模拟模型

在特定海区季节和风浪存在明显的周期性变化规律，导致不同时期同一海区船舶交通事故频次不同，某一海区成为高风险海区。所以，船舶规避高风险海区需绕航。大风浪区更是如此，大风浪区具有鲜明的特征，例如太平洋中高纬（冬季）、北大西洋中高纬（冬季）等海区，冬季频发大风巨浪区。由于特定海区具有季节和地理位置特点因素，根据国际海事组织（IMO）统计的船舶海难事故，可得到船舶海上航行风险模拟分别情况。[9-10]

根据船舶海上航行风险分布特点，运用高斯模型进行模拟计算结果。高斯模型的优点是运用现实生活中普遍存在的非高斯数据概率函数量化后进行密度拟合，构成由诸多高斯概率函数形成的混合函数，符合本研究理论目的要求。[11-12]

本研究的理论中，混合函数可作如下表示：

式（1）和式（2）分别模拟船舶发生事故性险情和船舶海上航行险情的高斯风险分布情况。如果高斯模型待估参数均为非随机性数据求解，可采用函数最大化似然估计。以船舶海上事故性风险高斯风险模型为基础，待估风险参数ξB的似然估计函数为：

似然估计函数对于对数似然函数而言，可将求解待估参数ξB对数化而简便，获得对数似然函数：

从式（4）可知，采用先验经验值求偏导最大值而取得超越方程的多个解。为克服方程求解困难，采用EM法求解待估参数值。EM 法是利用最大可能似然估计从不完全数据聚类方法统计模型求解方法，具有收敛效率高、易实现的优点。本研究采用EM 法进行高斯模型参数估算。[13-14]EM 法以船舶海上交通险情事故高斯模型为例，通过以下四个步骤实现。

第一步，初始设置。从高斯分布情况设置高斯模型阶数及各子高斯待估参数初始数据值。

第二步，期望结果。将船舶海上交通险情待估参数初始数据代入式（5），求取第j 次船舶海上交通险情第h 子高斯分布密度，迭代步数用v 表示。

第三步，求解极大化。将船舶海上交通险情地理船位及船舶密度概率值代入式（6）、式（7）和式（8），对第h 个子高斯重新计算各待估参数。

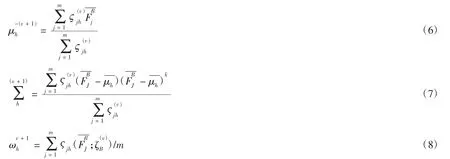
第四步，判断条件。如果满足要求条件则暂停迭代，选取迭代结果为高斯模型最优待估参数。如果不能满足要求条件，则返回第三步重新迭代。

计算得到高斯模型最优待估参数后，绘制航经海区风险分布图，并应用到船舶海上航线设计中。

2.2 船舶航行避险航线设计模型

在航运经营管理中，船舶营运以经济收益为第一目的，经济收益是决定设计船舶避险航线首要因素，因为绕航延长船期势必产生运营成本，所以三者间产生利益冲突时，必有选择。在最终决定船舶海上航行避险航线时，船舶吨位、类型和船公司决策者风险偏好决定了三大因素策略权重值不同[15]。

如上所述，将航经海区按长度单位设定为若干像元，每一海上交通险情风险值对应一像元，经济收益成本和发生事故性险情值，可得出综合考虑了风险偏好的船舶海上航行风险成本计算公式：

式（10）考虑了同一像元船舶发生事故性风险险情风险值，海上交通险情风险值和航运经济收益成本的大小，并综合考虑了船舶风险偏好给予的不同策略权重，获取该船偏好后的风险成本图。得到成本图后可使用Dijkstra 法计算从出发航点到终点间距离成本求解。按照成本累积不减原则从出发航点开始逐渐延伸到结束，从而获得最小成本、最短航线路径。

如上所述，综合考虑船舶偏好的海上航行避险航线设计模型需按如下步骤完成：

第一步，准备数据。最小成本、最短航线距离法需两大数据，即出发航点数据和成本数据。出发航点数据定义了源头像元的地理位置，本研究中对应船舶出发泊位。成本数据表示没有像元成本值。根据像元大小，运用高斯模型模拟获取两种风险分布情况图是计算获取的最初始数据，经标准化处理后，得到航行风险分布图。此外，成本航运经济收益成本具有不可预测性，需要根据自身特点和标准化处理得到。

第二步，转化数据。应用于成本距离算法经标准化处理后的风险数据为离散型，所以需对风险情况分布图重新进行分类处理。

第三步，计算成本。成本距离算法源于Dijkstra 法，因Dijkstra 法将每一像元视为一节点，各节点相互连接，每一像元存有一成本值，节点连接也需不同的成本，对应船舶海上避险航线设计模型，需付出相应风险的最短路径计算方法。例如图 1（a）所示，设定像元序号为 0，1 和 8 的成本为 d0，d2和 d8，则连接成本值 d（0，1）=（d（0）+ d（1）/2）。如果 d（0），d（1）和 d8风险值分别为 2，3，4，则 d（0，1）= 2.5，d（0，8）= 3.0。

第四步，赋予初始值。首先赋予像元成本值为0，并将其输入网格，再运用第三步中方法计算其他有效像元的连接成本，并按大小顺序输入列表。

第五步，寻找路径。选择列表中最小的像元作为首选成本像元，并输入网格，激活其他像元，输入列表，将像元到其他像元的连接成本继续计算，已经输入网格的像元不再重新计算。以图1（a）作为例证，若计算后寻找到 d（0，8）为最小成本，将图 1（a）新选 8 作为新的像元，并重新编排序号为 0，并激活其他像元，如图 1（b）所示。

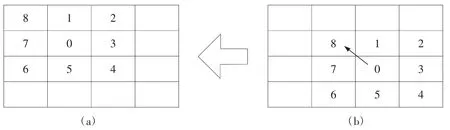
图1 像元成本示意图

第六步，迭代操作。对第五步重复运作，直到表列为空。寻找网格图中像元的最小成本，从而获取开始点到其他像元的最小成本。同时，寻找操作计算中每次迭代路线，即船舶海上航行避险航线。

3 验证分析

本研究选用中国黄渤海水域作为模型应用的分析对象，分析水域为老铁山到成山角附近水域。首先，根据中国海事局官方数据，辽宁海事局和山东海事局辖区2016—2020 年发生航行险情分别为467 起和519起，事故性险情分别为215 起和212 起。因为恶劣天气大风浪致使船舶事故性险情具有季节性，而其他船舶航行险情与船舶自身和外部环境有关，所以选取2016 年航行船舶事故性险情风险事故与航行险情事故相关数据。

本研究采用高斯模型对原始数据两种风险因素分布密度进行模拟，将原始数据经、纬度分别转换为x、y轴坐标值，采用MATLAB R2014 软件进行模型参数计算。经对比似然函数可以看出，海上船舶事故性险情风险模型最良子分布数为4，L 为-722.7471，船舶航行险情风险模型最良子分布数为2，L 为-291.2。计算参数如表 1 所示。

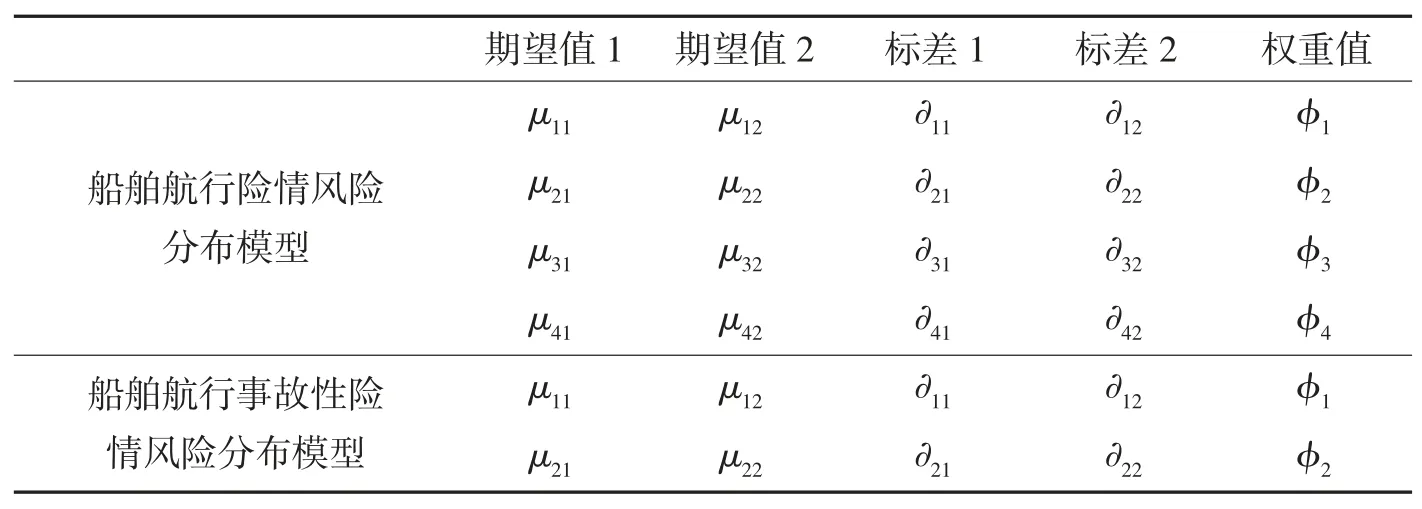
表1 船舶航行潜在风险模型参数计算表

根据已有的高斯模型各个参数值，可绘出船舶航行事故性险情风险事故和船舶航行险情风险事故密度分布图，为了方便理解和计算，将船舶航行事故性险情风险事故和船舶航行险情风险事故密度分布进行标准化优化，船舶航行事故性险情风险事故密度分布赋予最大值为10，因为该点是两大风险密度分布的最大值，所以选择此点，此后以倍数形式对所有点风险密度分布标准化优化，可得到标准优化后的船舶航行事故性险情风险数值和船舶航行险情风险数值分布图如图2、图3 所示。

图2 标准化处理后的船舶航行事故性险情风险分布图

图3 标准化处理后的船舶航行险情风险分布图

因为本研究综合考虑了船舶航行风险偏好而进行的海上航行避险航线设计，所以依据船舶航行事故性险情分布、船舶航行险情分布及经济收益不同权重进行组合。对船舶航行事故性险情风险分布和船舶航行险情风险分布均进行标准化优化处理，获取风险数值分布，但经济收益分布未知。综合以往经验及两大风险数值分布和自身经济收益分布特征，假设经济收益的分布是数值等于1 且在研究海域内均匀分布。

本研究运用Arcgis 软件设计船舶航行避险航线。根据模型第二步期望结果的要求对数据进行转化，采用10 个标准化等级，进一取整优化分类出离散数据。船舶航行决策者的偏好不同而决策各异，所以需全面考虑不同偏好选取最佳的海上航行避险航线。但是，作为航运公司追求经济利润是第一位的，其次是航行风险因素。综合考虑用数学语音表达应满足依据决策权重因子风险因素各异精确度而不同，即使进行全部组合重新计算分析也会有千差万别的组合结果，况且这也不现实。鉴于以往研究成果，本研究以0.1 为一单位，选择13 种偏好且满足的组合进行例证分析，组合情况如表2 所示。

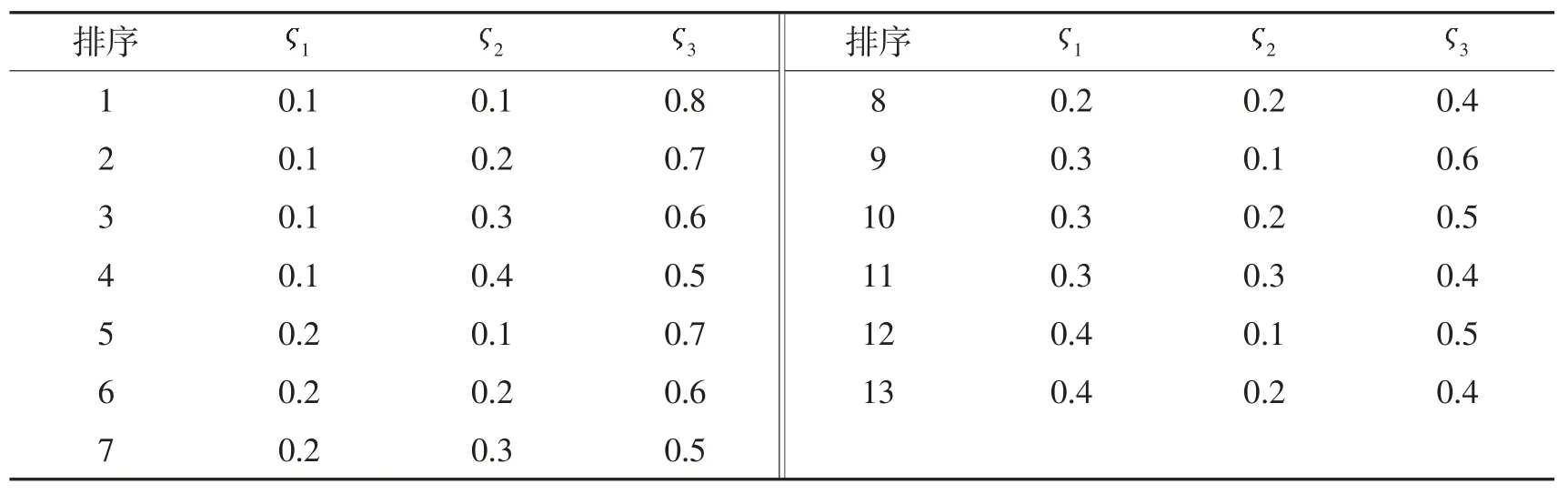
表2 满足要求的权重组合表

在表2 中组合基础上综合考虑船舶偏好进行船舶航行避险航线设计，可根据海事局VTS 船舶实时动态分布特点，结合我国黄渤海航行实际，选取从渤海经长山水道或老铁山水道驶入成山角附近水域的三条航线。线路1 从渤海某港口经长山水道（含庙岛水道）进入成山角附近水域，线路2 从渤海某港口经老铁山水道南下到烟台港以北转向东航入成山角附近水域，线路3 从渤海某港口经老铁山水道航入成山角附近水域，如图4 所示。

图4 综合考虑了船舶偏好的船舶航行避险航线示意图

从图4 中13 种航线偏好得到的船舶航行避险航线看，线路3 最简单，每一路线都能直接驶入成山角附近水域，只是船舶转向点船位不同，但是都能不绕航驶入成山角附近水域，而线路1 和线路2 出现了不同程度的绕航。例如线路1，不管如何取值，其设计的航线均有不同程度的绕航，随着1值增大，前段航程绕航明显，而2值决定中段航程的绕航，所以两者共同影响了线路1，从而这是一条绕航航线。从图4 可知，线路2 在进入老铁山水域前不需要绕航，具有其他偏好的船舶航行决策者可选择绕航。由此可知，当1权重值较小时，线路2 的前段航线不需要绕航，当1值增大时，航线中段出现了明显的绕航，将设计航线和船舶航线实际情况比较，以检验设计的避险航线是否合理。线路3 中少量碍航物不需要绕航，而线路1 和线路2随船舶航行事故性险情风险决策权重和船舶航行险情风险权重增大，均会出现不同程度的绕航，以便选取相对风险小的航线。但无论绕航多少，都看出经济收益这一决策权重的关键作用。综合上述，可得出一条综合船舶偏好的合理的船舶航行避险航线。

4 结束语

本研究在高斯模型模拟船舶航行风险的基础上，采用距离成本算法得出了综合考虑船舶偏好差异的船舶航行避险航线，并选取我国黄渤海部分水域船舶航行事故性险情风险事故和船舶航行险情风险事故数据做案例分析，获得船舶航行避险航线。结论表明，船舶航行决策者的偏好对线路1 和线路2 影响较大，但对线路3 几乎没有影响。本研究提出的既考虑船舶航行可能面临的风险，又照顾到船公司经济效益设计的航线具有很强的经济效益性，同时，对船舶航行决策者偏好差异进行了差异组合，使得应用高斯模型设计避险航线具有很强的实际意义。