兼顾公平和效率的养老机构空间配置优化研究——以上海市闵行区为例

程 敏，崔 晓

(1.上海大学 管理学院,上海 200444; 2.同济大学 经济与管理学院,上海 200092)

0 引言

近年来，我国老龄化进程加快，养老机构作为老年人养老的主要场所之一，在解决养老服务问题方面发挥着重要作用。公平和效率是公共服务设施配置的重要目标，旨在以尽可能少的投入提供尽可能均等的公共服务。养老机构配置的合理性决定了城市养老服务的能力。当前，我国养老机构还存在床位缺口大、空间布局不合理等突出问题，严重影响了养老服务质量和服务能力，也阻碍了养老机构配置公平与效率目标的实现[1]。因此，有必要对养老机构的配置优化问题开展研究。

国内外养老机构的相关研究主要关注老年人机构养老意愿[2-3]、养老机构可达性[4-5]、影响养老机构发展的因素[6-7]等方面。目前，仅有少量研究从3个方面关注养老机构的配置优化问题：一是从规划学角度，采用单床建筑面积、每百位老人拥有床位数等比例指标分析养老机构配置现状，提出优化配置建议[8]。该方法计算简单但考虑因素不够充分。二是从社会学角度，在实地调研机构养老需求基础上提出养老机构优化配置对策[9]。这类研究通常仅考虑机构及其床位数量上的优化，未考虑机构空间布局。三是从地理学角度，通过空间计算探讨养老机构配置合理性和优化方案[10]。这类研究侧重空间布局优化，缺少对设施数量的关注。上述研究仅关注到养老机构数量优化或空间布局优化中的一个方面，具有一定的局限性。

公共服务设施的配置需兼顾公平与效率，现有研究大多采用经典的设施区位-分配模型，仅重点关注设施配置的效率问题[11-12]，少量以公平性为目标的研究则未考虑配置效率[13]。养老机构的配置既要合理规划机构数量，又要科学布局区位，还要兼顾公平与效率，是典型的带有复杂约束条件的多目标非线性动态决策问题。目前，较少有研究关注多目标下同时对养老机构的数量与空间布局进行优化。遗传算法是经典的求解复杂优化问题的方法，但随着求解问题的复杂化，其表现出极易陷入局部最优、求解效率低下等缺点，需加以改进以提高算法性能[14]。虽然智能优化算法可用于研究复杂系统结构和动态行为，但在空间决策上还存在不足。地理信息系统(GIS)作为有效的空间分析工具，可为复杂空间决策提供支持，并实现可视化。因此，将改进遗传算法与GIS相结合可以更好地解决空间优化问题[15]。

当前我国老年人数量增长较快，为使养老机构的设施配置具有前瞻性，应基于未来老年人口数量的预测研究其配置优化问题。本研究以公平和效率最大化为目标建立养老机构空间配置优化模型，以上海市闵行区为例，先从数量、规模和区位3个方面分析现有养老机构的配置现状，然后预测其老年人口峰值及区位分布，再根据人口预测结果，采用改进遗传算法和GIS技术对模型进行求解并实现空间布局可视化，提出配置优化方案，最后探讨优化结果的合理性和算法的优越性，为区域养老资源的合理配置提供参考和依据。

1 研究方法

建立养老机构配置优化模型，并基于对老年人口数量的预测，采用改进遗传算法对模型求解，从符合选址要求的J个养老机构候选点中选择p个最优区位点，以满足I个居民点未来机构养老需求。

1.1 养老机构配置优化模型构建

养老机构属于公共服务设施，政府在其配置决策时会力求在一定成本范围内使居民尽可能公平、高效地获得养老服务，即兼顾公平和效率。因此，以最大化公平性和最大化效率为目标建立养老机构配置优化模型。

1.1.1最大化公平性。公平性体现在每位老年人能均等地获得机构养老服务。养老机构配置的均衡程度可以通过居民点到养老机构的可达性差异来反映,可达性差异越小，表明养老机构配置越均衡，公平性也就越大。计算公式为：

式中：j为养老机构候选点；J为所有养老机构候选点的总数；vj为养老机构候选点j的供给量，用可提供的床位数表示；β为距离衰减系数；dij为居民点i到养老机构候选点j的最短道路距离(不考虑道路的等级、宽度、步道等辅助要素)；Yj为0-1变量，如果候选点j被选为最优区位点，则Yj取值为1，否则Yj取值0。

1.1.2最大化效率。效率分为使用效率和经济效率，使用效率指老年人的机构养老需求得以满足的程度，经济效率则反映养老机构投入资金的经济效益。①最大化使用效率。采用改进P-中值模型计算各居民点到养老机构的总加权出行成本，以表征养老机构的使用效率。出行成本越低，表明越多的老年人可就近享受机构养老服务，养老机构的使用效率就越高。传统的P-中值模型采用“邻近原则”，追求居民点与最邻近的机构点之间的总出行成本最小化，以实现机构使用效率最大化，但现实中老年人通常会在多所养老机构之间权衡选择。老年人选择某机构的概率除与出行成本有关外，与该机构的吸引力(一般表征为规模)也存在一定的关系[11]。因此，将吸引力因子(Aij|Ai)引入传统P-中值模型，构建新的总加权出行成本模型。计算公式为：

式中：E为投资建设养老机构的经济效率；Rj为养老机构候选点j的利润；c0为人均收费；c1为单床运营成本。根据实际情况，取c0=2 050元/月,c1=1 250元/月；Zij为0-1变量，表示居民点与养老机构的对应服务状况，若养老机构j服务于居民点i，则Zij=1，否则Zij=0。此外，在配置养老机构时还需关注以下要求：一是需从养老机构候选点中选取p个最优区位点；二是各居民点均可获得一个养老机构的服务；三是任一被选定的最优区位点均服务于相应的居民点；四是符合《养老设施建筑设计规范》(GB 50867—2013)规定的各类型养老机构床位数量的配置标准。

1.2 遗传算法的改进

遗传算法模拟生物进化过程，使群体经历多次遗传、交叉和变异等遗传学变化，并利用适应度值(模型中的目标函数值)评价群体中个体对环境的适应程度，在适者生存的作用机制下，群体经历不断更新换代，并在整体范围内寻找群体中的最优，直到获取最理想的求解结果。由于遗传算法在自身收敛性上存在不足，容易陷入局部最优，且计算效率不高。为改进传统遗传算法的早熟缺陷，引入自适应交叉率[16]，即当个体的适应度值较小时，高交叉概率可提高其更新速度；当适应度值较大时，低交叉概率可帮助保留优良个体。另外，传统遗传算法中固定变异率的选取会影响计算结果，即当变异率较小时，种群往往会早熟；而当变异率较大时，不但会使收敛时间显著增加，寻优效率也会明显下降。因此，借鉴动态变异率[16]以提高算法寻优能力。此外，由于遗传算法本身并不具有直接求解多目标问题的能力，采用适应性权重方法将多个目标函数值标准化后加权求和，从而获取遗传算法的适应度值。

1.3 人口预测方法

常见的人口预测方法主要有自回归移动平均模型、曲线模型、人口年龄移算模型、灰色系统模型等。其中，等维递补灰色预测法可实现动态预测，使长期预测结果更贴近实际[17]；人口年龄移算模型是相对稳定的人口预测方法，模型简单，易于实现[18]。因此，将等维递补灰色预测法和人口年龄移算模型相结合对具有机构养老需求的老年人口(本研究界定为60岁及以上)数量进行预测。由于计算过程涉及未来年份老年人的死亡率，因此，先采用等维递补灰色预测法对死亡率进行动态预测，以提高预测的精确度，再利用人口年龄移算法对未来机构养老人口数量进行预测。

2 研究对象与数据来源

2.1 研究对象

以上海市闵行区为研究对象。闵行区下辖9个镇、4个街道和1个市级工业区，有132个村民委员会、427个居民委员会。2020年，闵行区老年人口有37.9万人，占总人口的比例高达31.8%，是上海市老年人口最多的区，人口老龄化严重。然而，闵行区目前仅有养老机构41家(图1)，可供床位数仅为10 319张，尚不能满足老年人的养老需求。

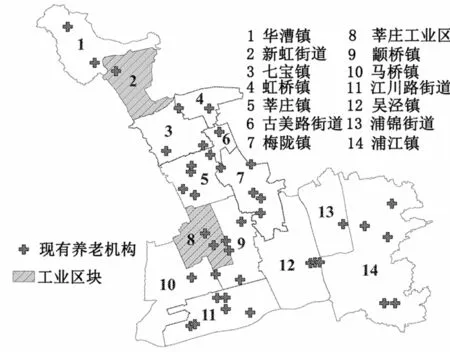
图1 闵行区现有养老机构分布

考虑到居住在闵行区边界的老年人也有可能选择到相邻区县寻求养老服务，为消除这一边界效应的影响，在闵行区周围建立一定距离的缓冲区，对闵行区及其缓冲区开展空间分析，并通过空间剪裁得到研究区最终的养老机构配置结果。参考相关研究[4,13]，老年人普遍可接受1 h车程距离以内的养老机构。因此，将缓冲区宽度设定为1 h车程距离。

2.2 数据来源

2020年老年人数量等相关人口数据通过闵行区统计年鉴及上海社区服务网获得，各养老机构的床位数据从上海市民政局官方网站获取。交通网络通过ArcGIS软件平台构建，采用Network工具计算居民点到养老机构的最短路径距离。

根据《城镇老年人设施规划规范》(GB 50437—2007)，养老机构应选址在具有良好基础设施条件且交通便捷的地段。为得到养老机构的候选点，参考相关研究[19-20]设置公园绿地、医疗机构等基础设施及道路的服务缓冲区半径，并采用ArcGIS软件对其进行缓冲区分析和重叠分析，产生满足选址要求的养老机构候选区域，再综合考虑居民点楼宇位置，在候选区域里设定了580个养老机构候选点。

需明确距离衰减系数β的取值，以计算养老机构的可达性。优化后养老机构的位置会发生较大改变，致使其到居民点的道路网集发生变化。因此，优化前后需选取不同的β值。根据D.Peeters等的研究，β的取值集中在0.90～2.29[21]，本研究在0.8～2.4之间以 0.2为间隔设定9个不同的β值，分别计算9种情景下居民的出行时间，并将其与调查获取的居民实际出行时间比较，发现β=1.8时的计算结果比较符合实际，可用于计算现状养老机构的可达性。进一步探讨养老机构配置优化计算时的β取值，将机构数量在1～41范围内取不同数值，分别计算不同的机构数量在β取不同数值时优化后的养老机构可达性值，均可发现当β=1.0时优化后的养老机构可达性标准差最小，与现状下的养老机构可达性标准差的差距最大，说明此时各机构的可达性差距最小，公平性最好。因此，选取β=1.0计算优化后养老机构的可达性。

3 结果与分析

3.1 人口预测结果分析

对闵行区老年人口数量的预测结果表明，2040年是闵行区老年人口峰值年，为39.334万人。其中，有机构养老需求的老年人有13 767人。当前，闵行区老年人口分布为从中心往外递减，近郊区老年人口密度较小，且南北区域差异不大。根据人口预测，未来闵行区近郊区老年人口增长较快，特别是北部区域增长速度明显高于东南和西南部区域，且工业区内老年人口呈逐渐迁出趋势，老年人口空间分布将呈现中心区域较高、东南和西南区域较低的分布特点。

3.2 养老机构配置现状分析

3.2.1养老床位数量分析。闵行区现有的41家养老机构可供床位为10 319张，根据对有机构养老需求人口的预测，2040年需配置13 767张养老床位，即需新增3 448张养老床位。参考相关研究[4,20]，设定养老机构的有效服务半径为1 h车程，计算各居民点百名老人的可达床位数。在1 h车程有效服务半径下，仅有40.23%的居民点满足《上海市养老设施布局专项规划(2013—2020年)》中提出的“百名老人3.5个床位”要求，供应数量存在较大缺口。

3.2.2规模分析。当前，闵行区中部的七宝镇、虹桥镇、莘庄镇、古美路街道、梅陇镇等街道养老机构的床位数仍存在较大缺口，亟需对现有养老机构进一步优化扩建。闵行区北部的华漕镇以及南部的颛桥镇、马桥镇、江川路街道、吴泾镇、浦锦街道、浦江镇等街道人口规模相对较小且分布相对松散，部分养老机构配置规模较大，部分则供不应求。此区域为快速城镇化区域，是人口导入的重点区域，因此，需结合未来人口发展情况在调整现有机构规模的基础上进行增设。在新虹街道和莘庄工业区等工业区块内，大多数养老机构规模配置过大，造成资源浪费，宜优化规模。

3.2.3区位分析。从580个候选点中计算选出与当前养老机构数量相同的养老机构最优区位点，将其与现有养老机构的区位进行比较(图2)。可以看出，一些养老机构偏离最佳区位，使用效率较低，尚未实现公共服务设施的公平分配，需对该区域养老机构配置进行优化。

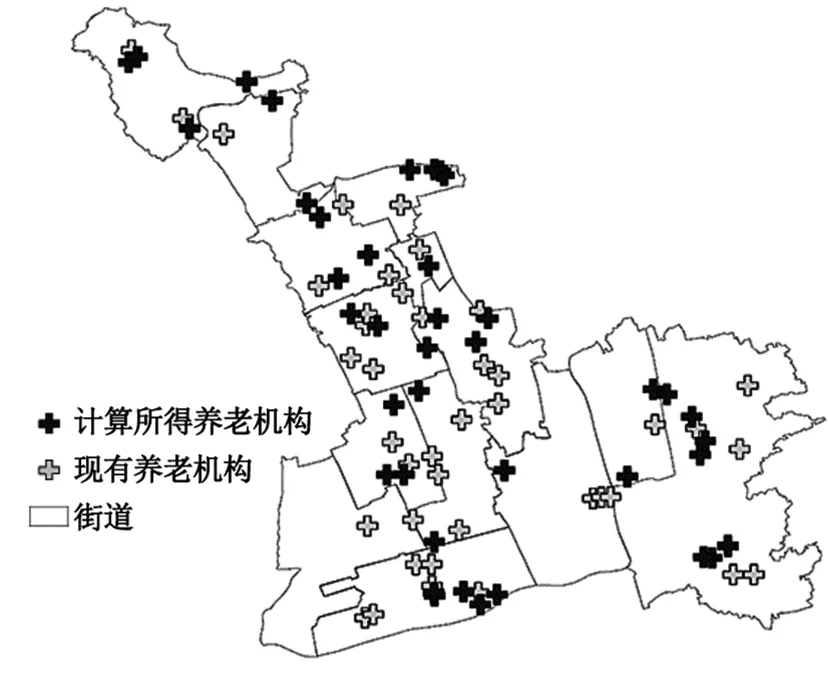
图2 计算选取的养老机构与现有养老机构的区位比较

3.3 养老机构配置优化模型应用

根据闵行区有机构养老需求的老年人口的预测结果，对养老机构的配置进行优化。首先，计算得到区位不合理需调整的养老机构，对其余养老机构进行规模调整，实现调整性优化；其次，识别出经调整性优化仍未满足机构养老需求的居民点，通过改进遗传算法求解优化模型得到需增设的养老机构数量和位置，并根据其与居民点的服务对应关系，确定各增设机构应配置的床位数，实现规划性优化。

3.3.1养老机构调整性优化(图3)。在现有养老机构数量和规模有限的情况下，有3所养老机构因周边养老机构较为集中、老年人口数较少等原因导致其床位供需严重不匹配，在原区位运行不合理，宜调整其区位。根据《养老设施建筑设计规范》(GB 50867—2013)对养老机构最大配置规模的规定及居民点机构养老需求人数，调整其余38所养老机构的规模，确定优化后养老机构床位数与现状养老机构床位数的差值，正值表示需增设机构床位，负值则表示机构床位数量需要减少(图3a)。进行调整性优化后，剩余38家养老机构在原区位运行只能满足10 895人的机构养老需求，仍有2 872人的机构养老需求未得到满足，需增设养老机构(图3b)。

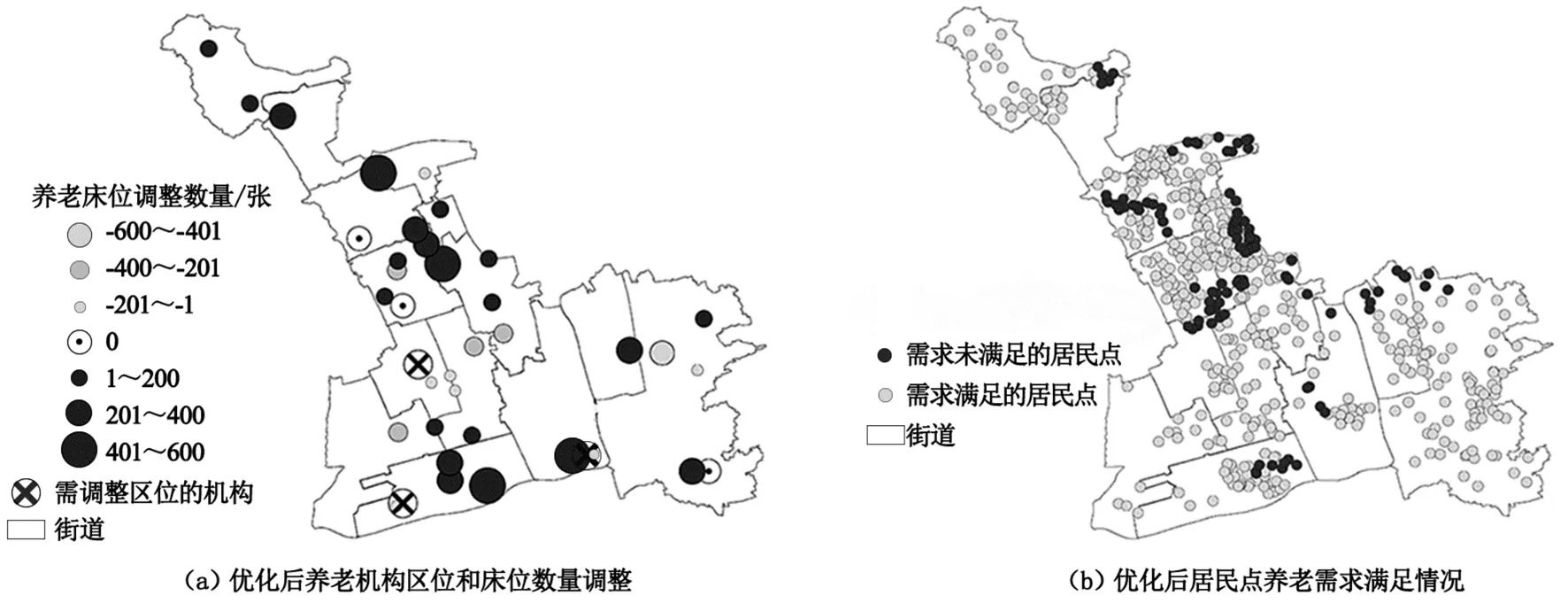
图3 调整性优化结果Fig.3 Adjustment and optimization results

由图3可知：① 对于闵行区中部地区，尽管人口数量趋于稳定，但为满足增长的养老需求，仍需在扩大规模的基础上新增较多养老机构弥补供需缺口。② 对于闵行区北部和南部地区，由于该区域是下一阶段人口导入的重点区域，当前闲置养老机构床位在未来会得到充分利用，部分存量机构亦需提升改造、挖掘潜力、增设床位。同时，有两所养老机构因分布集中造成资源浪费，宜调整区位。在此基础上，未来仍有部分老年人的机构养老需求未能得到满足，需新增养老机构给予补充。③ 对于工业区块，由于工业发展会影响养老服务质量，不宜配置过多数量的养老机构，该区域有1 所机构在现有区位运行欠合理，且大多数养老机构规模可适当压缩，以提高利用效率。

3.3.2养老机构规划性优化。规划性优化是指在养老机构供给不足区域进行新增机构规划选址和规模安排。首先，需确定要新增的养老机构数量。根据《养老设施建筑设计规范》(GB 50867—2013)，养老机构最大规模一般不超过500人。调整性优化结果表明，到2040年全区有2 872人的养老需求还得不到满足，因此，需至少增设6所养老机构。采用改进遗传算法对构建的养老机构配置优化模型进行求解，计算得到不同养老机构数量时的适应度值(表1)。适应度越低，养老机构配置优化结果越好。因此，新增13所养老机构较为合理。

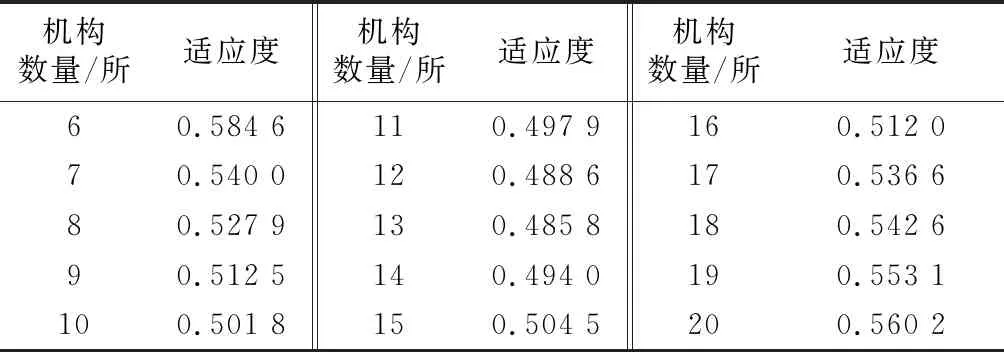
表1 不同机构数量的适应度值Tab.1 Fitness values for different numbers of residential care homes

在养老机构候选点中选取13处作为新增机构(图4)。新增养老机构服务的居民点中老年人数量之和，即为该新增养老机构需配备的床位数。需增设的养老机构位于七宝镇、虹桥镇、莘庄镇、古美路街道、梅陇镇等闵行区中部地区，以及华漕镇、江川路街道、浦锦街道、吴泾镇等街道的边界处，此处老年人口数量较多，当前养老床位数量不足以满足养老需求，增设一定数量的养老机构有助于实现供需平衡，推动养老事业健康发展。

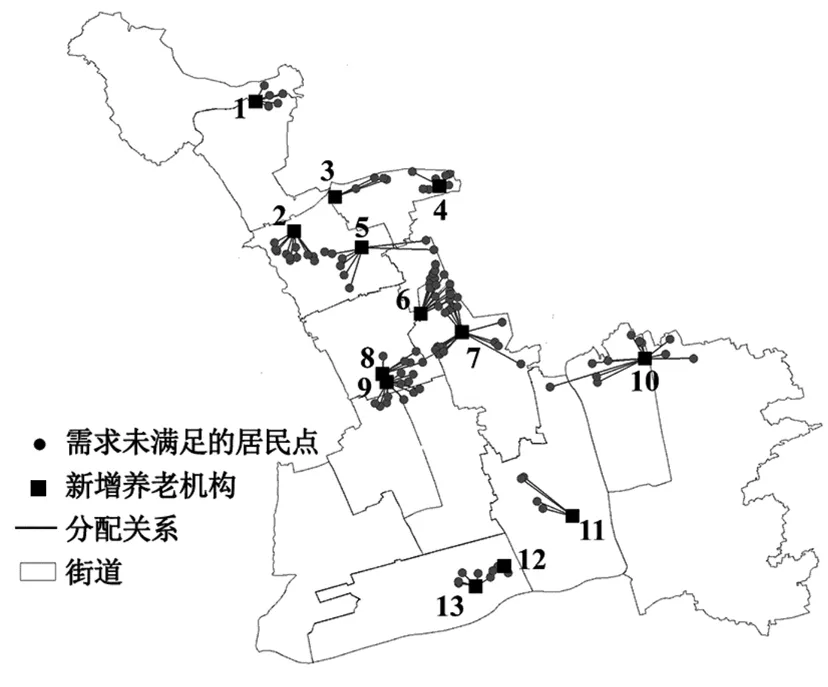
图4 新增养老机构位置及分配关系

3.4 优化结果合理性及算法优越性分析

3.4.1优化结果合理性分析。比较优化方案与现有方案，说明优化方案的合理性。① 养老机构空间配置公平性更佳。优化后的配置方案在公平性方面相对于现有方案优化率达到59.71%；居民潜在可获取服务资源量的基尼系数从0.498 1降至0.193 2(基尼系数越低，公平性越高)；82.41%的居民点优化后的可达性与加权平均值的比值介于0.9～1.1，说明优化后绝大多数居民点居民能公平地获取机构养老服务。② 养老机构空间配置效率提升。养老机构的使用效率和经济效率都得到了提升，优化后的养老机构布局以需求为导向，机构分布更加均衡，更有利于改善配置效率。③ 居民出行更加便捷高效。81.87%的居民点出行效率得到了改善；大部分居民点附近至少有1 所养老机构。居民点至邻近养老机构最大出行距离由8 572 m降至3 380 m，平均出行距离由1 505 m降至941 m，各居民点1 h出行时间平均可达床位数由3.16 提升至4.14。

3.4.2算法优越性比较。为验证改进遗传算法的收敛性和计算精度，对各算法的优化过程进行比较。利用4种算法分别进行计算，改进遗传算法运行时间仅842 s，其求解效率与粒子群算法、模拟退火算法、一般遗传算法相比分别提高了49.82%，32.75%和9.85%，求解精度分别提高了27.85%，38.17%和15.15%。改进遗传算法有良好的收敛性、运行效率及运行结果。

4 结论

基于公平性和配置效率最大化构建多目标带约束的养老机构配置优化模型，并将改进遗传算法与GIS技术相结合，进行模型求解与分析。以上海市闵行区为研究区域，对老年人口峰值数量进行预测，提出养老机构优化配置方案，实现了数量、规模、区位上的同时优化，并进一步分析了优化方案的合理性及算法的优越性。

上海市闵行区现有养老机构在数量、规模、区位等方面还不能满足区域人口快速老龄化发展需求，亟需根据未来人口发展特点，对现有养老机构进行优化。根据计算，现有养老机构中有3所区位不合理，部分现有养老机构需适当调整规模，另需增设13所养老机构以满足未来机构养老需求。通过比较发现，优化后的养老机构公平性和配置效率均得到改善，改进遗传算法相对其他算法在此问题中有良好的计算精度和运行效率。本研究提出的优化配置方法也可用于其他类型的公共服务设施，为有关部门规划决策提供理论支持。