极值Ⅰ型分布设计安全修正值系数的研究

王晓惠，潘晓春，沈旭伟

（中国能源建设集团江苏省电力设计院有限公司，江苏 南京 211102）

根据现行《港口与航道水文规范》，海港工程极端高水位、极端低水位、设计波高及波周期等要素的分析计算可分别采用极值Ⅰ型、Pearson-Ⅲ型概率分布模型，也可以根据实测资料拟合最佳的原则，在两个分布模型之间择优选取[1]。此外，包括海港工程在内的结构抗风设计风速统计，也常采用两个分布模型进行分析计算[2]。

我国设计洪水计算推荐采用Pearson-Ⅲ型概率分布模型，并以设计值的均方误差作为安全修正值来估算抽样误差，通过设计值加上对应频率安全修正值，以确保计算成果的可靠[3]。安全修正值由安全修正值系数B 值、样本标准差及样本容量综合确定，同时与概率分布模型的参数估计方法密切相关[4-10]。目前关于Pearson-Ⅲ型概率分布模型的安全修正值系数B 值已有较多的研究[4-10]，有代表性的成果已被我国规范采用[3]，并应用到工程实践中。然而，现行相关技术标准[1-2]在推荐采用极值Ⅰ型分布模型进行频率分析计算时，仅进行不同频率设计值的点估计，未要求对设计值进行区间估计，忽略了样本抽样误差对设计值的影响，这对海洋水文实测资料短缺海区的海港工程设计极端高低水位和设计波要素可能带来可观的误差。

目前对极值Ⅰ型分布模型的抽样误差的研究较少，未见关于该分布设计安全修正值及系数的相关研究，本文通过统计试验（即Monte Carlo Method）推求基于Gumbel 参数估计方法的极值Ⅰ型分布模型的安全修正值系数B 值、B′值诺模图，并与Pearson-Ⅲ型概率分布模型的B 值诺模图进行比较验证，供工程实践尤其资料短缺的海港工程设计中参考使用。

1 理论与方法

1.1 设计值抽样误差的一般表达

潮位、波浪等海洋水文极值系列是未知的无限总体，而实测资料系列只能是有限样本，用有限样本估计总体参数必然存在不可避免的抽样误差，即由样本的特征推算和估计总体的特征而引起的误差。

用各种估计方法可对随机变量系列X 估得不同频率P 时的变数xP值，并绘出频率曲线。根据抽样原理，从频率曲线上读得的值是点估计值，在其两侧有一定的波动范围。如图1 所示，相应A 点对应的设计值xP隐含一个条件分布，其密度函数为f（xP|P）。此时，设在频率曲线上读得的估计值为xP，即A 点的纵坐标值，这是该条件分布的均值、中值、众值或别的特征值。

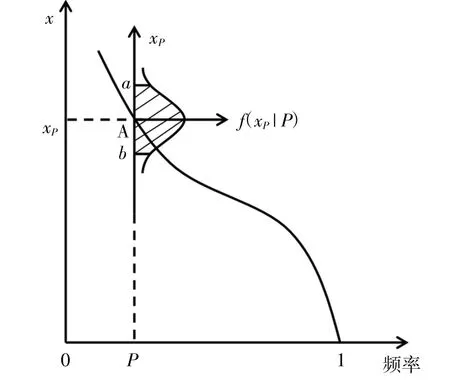
图1 频率分析设计值xP 的条件密度分布图[4]

1.2 统计试验推求B 值诺模图

极值Ⅰ型分布模型表达式如下。

式中，λP，n为极值Ⅰ型分布离均系数，其值可按式（12）计算或查JTS 145—2015《港口与航道水文规范》[1]附录表D.0.2。可见，JTS 145—2015 与GB 50009—2012 中的极值Ⅰ型分布的参数估计式的表达形式不同，但本质一致。

1.2.2 统计试验设计

现行技术标准推荐采用Gumbel 法进行极值Ⅰ型分布参数估计，为便于研究成果的实践应用，下文基于该法估计参数进行统计试验，研究样本设计成果的抽样误差，进而计算B 值。统计试验具体步骤如下。

步骤1：样本序列的生成。为了保证计算结果的一致性和有效性，E（X）= 1，CV=（0.1，0.15，0.20），运用蒙特卡洛方法生成容量n=5、10、15、20、30、50、70 和100 的序列，每组生成N=500个随机序列作为1 个计算小组。

步骤2：统计参数的确定。按照上述式（8）、式（9）计算每组随机序列的尺度参数和位置参数。

周淑蘋女士为前任中西女塾皇后。民国十六年间毕业。各报争刊其玉影。……是晚女士之装束华丽冠全场。粉红色的衣缀以一大红花。衣外复披白狐黑大衣，色彩与式样可称时髦已极。女士之头上浩浩乎平滑无疆，是又不得不归功于司丹康矣。闻今日为其出闺佳期。记者深愿女士能始终得条件之保障。而享受携手白头之乐也。……闻夏璐敏女士为沪大西剧社社员，因家庭反对男女合演，故未加入云。 ”[12]5（图 8、图 9）《新闻报》1929年 3月6日刊载《值得登广告》，详细记载了该剧的本事：

步骤3：计算xP的均方误差SxP。采用式（4）确定每组随机序列的设计值xP，i（P=0.01%，0.1%，1%，2%，3.3%，5%，10%），对于n、E（X）、CV相同的500 组随机序列，计算其理论设计值x0P、小组均方误差每500组序列作为一个小组，分别计算10 000 组的SxP，求得10 000 组的平均值。

步骤4：计算B 值。对n = 5、10、15、20、30、50、70 和100 的序列，根据下式计算对应的B值序列。

步骤5：计算相对偏差。对n = 5、10、15、20、30、50、70 和100 的序列，根据下式计算对应的相对偏差δ。

1.3 统计试验结果分析

1.3.1 CV对B 值的影响

样本容量取10、20、30、50 和100，对应不同的CV值分别进行试验，B 值成果如表1 所示。可见同一样本容量下相同频率，B 值相当接近，可以认为B 值与CV值无关。

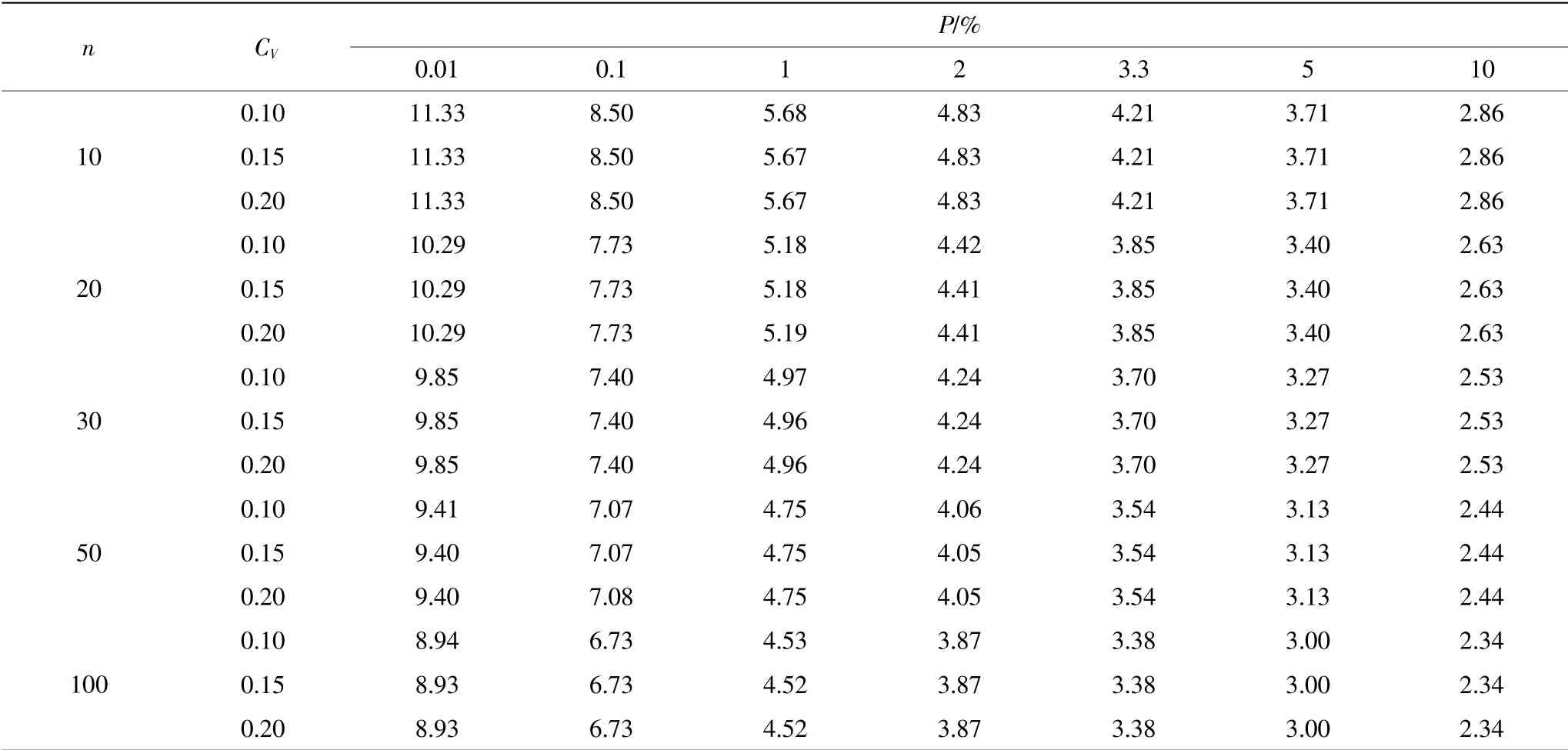
表1 不同CV 值与B 值的关系表（样本容量n=10、20、30、50 和100 共5 组）

1.3.2 样本容量对B 值的影响

1.3.3 B 值诺模图

根据上述分析，B 值与CV值无关，与样本容量n、频率P 关系密切。通过上述的15 组试验方案，统计试验10 000 次后，通过式（12）计算得到B 值表2 所示，绘制成B 值诺模图如图2。为使参数更加清晰，查图使用更加方便，令从而式（1）变为式（15）。

图2 极值Ⅰ型分布B 值诺模图

表2 不同样本容量与B 值的关系表（CV=0.10、0.15、0.20 共3 组，取均值）

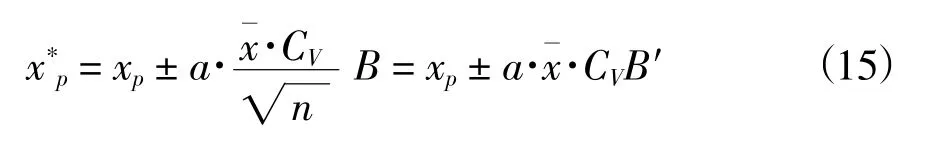
B′值及诺模图，分别如表3 和图3 所示。

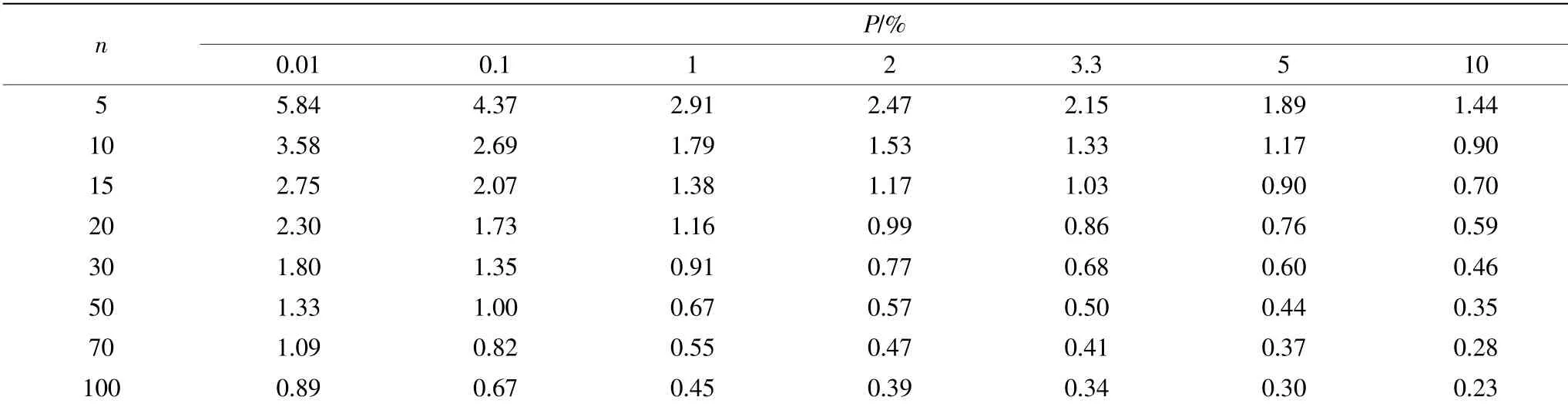
表3 不同样本容量与B′值的关系表（CV=0.10、0.15、0.20 共3 组，取均值）

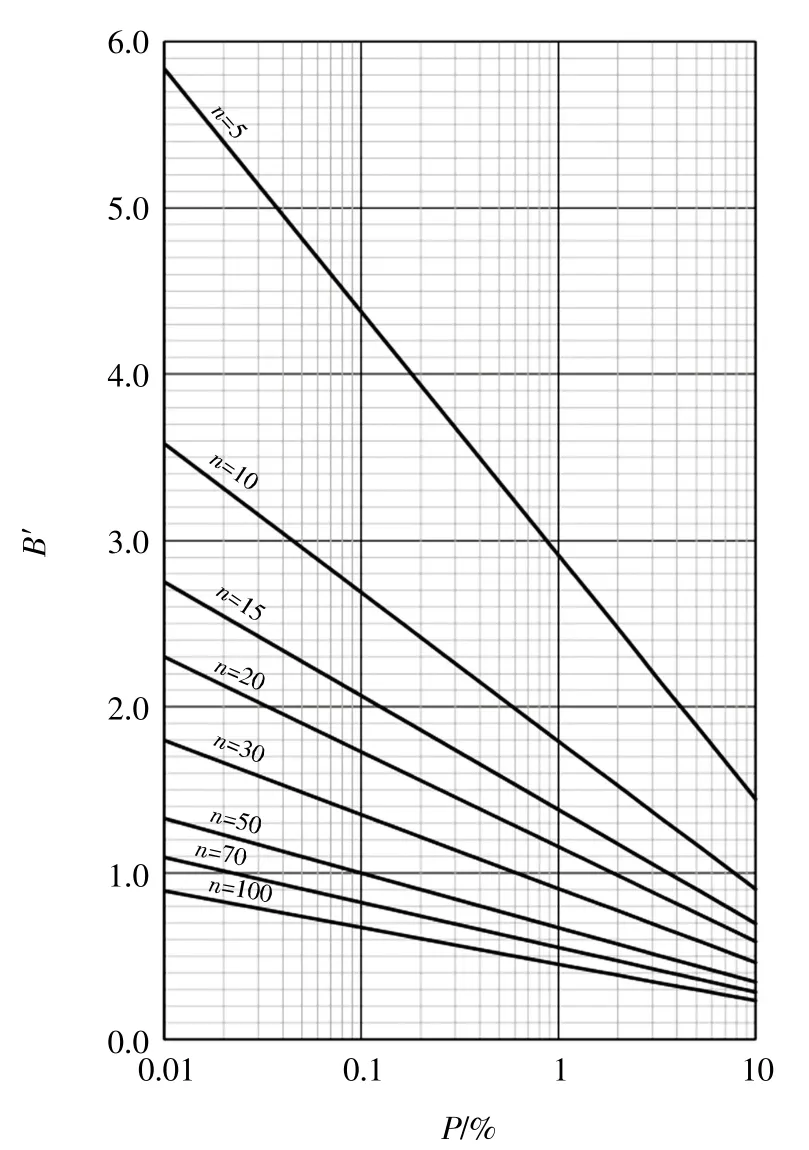
图3 极值Ⅰ型分布B′值诺模图

1.3.4 样本容量与相对偏差的关系

样本容量取5、 10、 15、 20、 30、 50、 70 和100， 对应不同的CV值（CV=0.1、 0.15、 0.2） 分别进行试验， 采用式（14） 计算样本容量引起估计值与真值的相对偏差， 如图4所示。 在值相同的情况下， 样本容量越小相对偏差越大； 样本容量相同的情况下， CV值越大相对偏差越大。

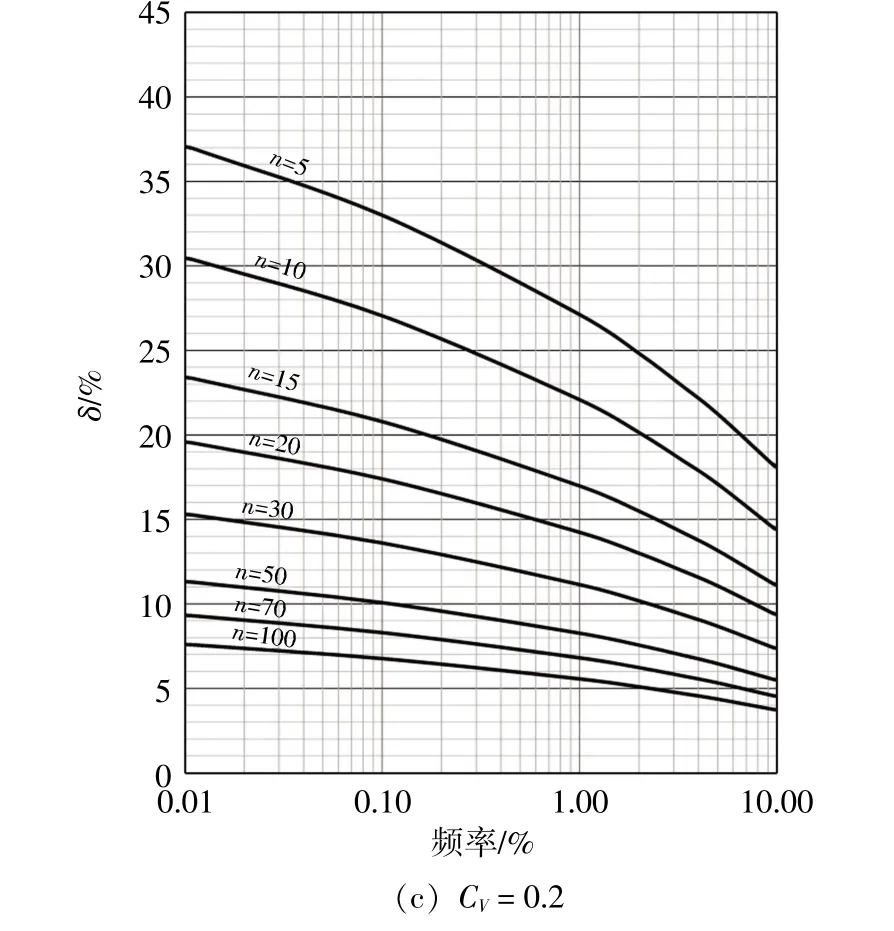
图4 不同样本容量引起的估计值与真值的相对偏差

2 极值Ⅰ型分布B 值的合理性分析

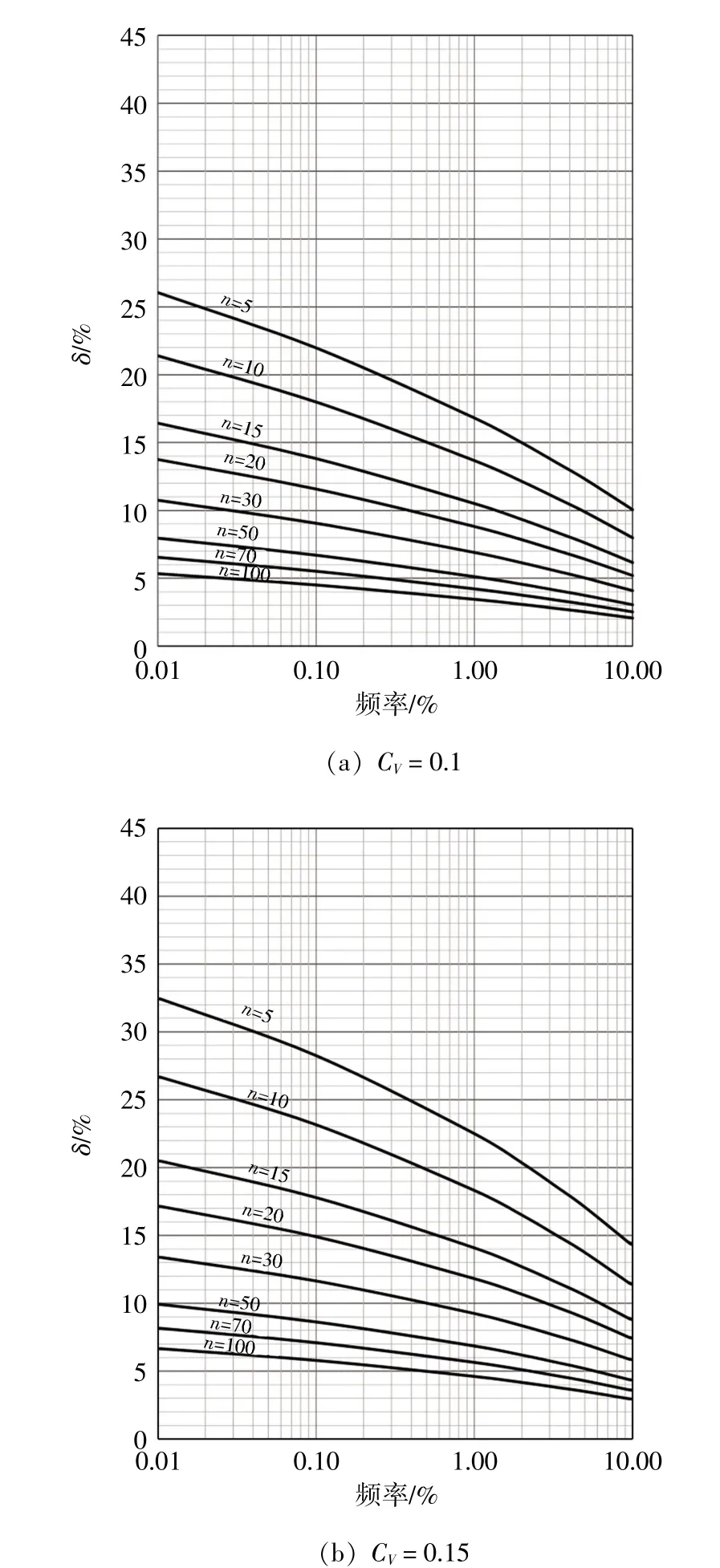
Pearson-Ⅲ型概率分布模型也被常用于水文气象要素极值的频率分析，许多学者及相关的规范采用了优化适线法、绝对值离差和最小法、最小二乘法、线性矩法等进行参数估计，并通过蒙特卡洛试验，得到了安全修正值系数B 值[3-10]。Pearson-Ⅲ型分布的B 值是CS与频率P 的函数，且与参数的估算方法密切相关。为与极值Ⅰ型的B 值对比，本文将n=5、10、15、20、30、50、70 和100 统计得到的B 值取平均值，并与Pearson-Ⅲ型CS= 0、0.5、1.0、1.5 的B 值进行比较分析。

丛树铮等[7]根据绝对值离差和最小（φ2-W）优化适线法，由统计试验方法计算得到了B 值图，如图5（a）所示；金光炎等[4]用统计试验方法，采用绝对值离差和最小法及最小二乘法适线法进行分布参数估计，绘制B 值诺模图，如图5（b）和图5（c）所示；刘攀等[8]认为线性矩法估计频率分布曲线的参数有较好的无偏性和有效性，并采用线性矩法估计Pearson-Ⅲ型的分布参数，绘制了用安全修正值系数B 值诺模图，如图5（d）所示。

图5 基于Gumbel 法估计的极值Ⅰ型与不同参数估计方法的Pearson-Ⅲ型分布的B 值诺模图

对于Pearson-Ⅲ型分布，在不同的参数估计方法中，当CS相同时，B 值由大至小依次为：最小二乘适线法、绝对值离差和最小法、线性矩法、绝对值离差和最小（φ2-W）优化适线法，其中绝对值离差和最小法与线性矩法参数估计相应的B 值非常接近。极值Ⅰ型分布的B 的均值介于Pearson-Ⅲ型分布CS= 0.5～1.5 的B 值之间。在频率P 较小时，极值Ⅰ型分布的B 值介于Pearson-Ⅲ型分布CS=0.5～1.0 的B 值之间；在频率P 较大时，极值Ⅰ型分布的B 值介于Pearson-Ⅲ型分布CS=1.0～1.5的B 值之间；频率P ＞4%，极值Ⅰ型分布的B 值与Pearson-Ⅲ型分布CS=1.5 的B 值大体相当。

3 实例分析

以某潮位站1989—2018 年共30 年历年最高潮位资料为例，进行设计高潮位实例分析。该潮位站1989—2018 年历年最高潮位序列的均值为1.77 m（珠江基面，下同），标准差为0.389，具体系列值如图6 所示。

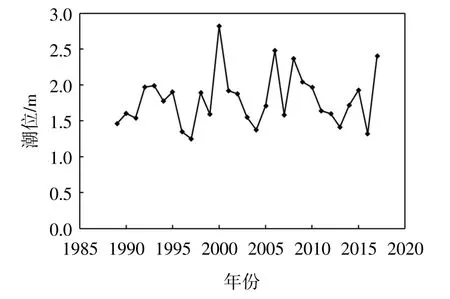
图6 某潮位站1989—2018 年历年最高潮位

3.1 不同频率分布模型的对比

采用极值Ⅰ型分布进行频率分析，参数估计采用我国标准推荐的Gumbel 法估计，得到位置参数μ=1.563，尺度参数α=0.359。采用Pearson-Ⅲ型分布进行频率分析，采用常用的φ2-W 适线参数估计方法得出CV= 0.26，CS/ CV= 4，对应的位置参数、尺度参数、形状参数分别为0.885、3.70、4.18。两个分布考虑安全修正值修正后得到的设计值及B 值汇总如表4 所示。

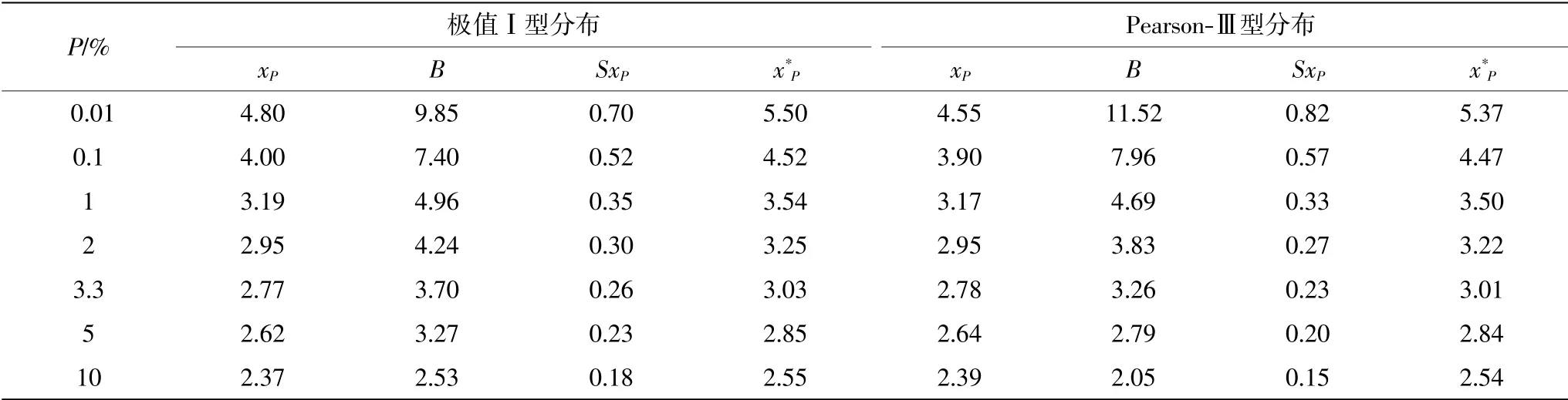
表4 极值Ⅰ型与Pearson-Ⅲ型分布修正后的设计值

极值I 型分布计算得到的设计潮位值xP较Pearson-Ⅲ型分布得到的成果略大，不同频率下差异约-0.02～0.25 m；在考虑安全修正值SxP后，两个分布得到的设计潮位值x*P相当，差异约0.01～0.13 m；频率越小，两个分布的差异越大，常用的P=1%、2%下，两个分布模型得到的xP、x*P基本一致。

在采用极值I 型分布分析计算设计潮位时，安全修正值SxP约为xP的7.6%～14.6%，约为x*P的7.1%～12.7%，即在不考虑安全修正值时，极值I 型分布分析计算设计潮位较x*P小约7.1%～12.7%。在采用Pearson-Ⅲ型分布分析计算设计潮位时，安全修正值SxP约为xP的6.3%～18.0%，约为x*P的5.9%～15.3%，即在不考虑安全修正值时，Pearson-Ⅲ型分布分析计算设计潮位较x*P小约5.9%～15.3%。本例充分说明了为得到更加可靠的设计潮位值，考虑安全修正系数修正抽样误差是十分必要的。

3.2 不同样本容量的对比

采用Gumbel 法对近30 年、20 年、15 年、10年、5 年的历年最高潮位资料进行设计潮位的计算，考虑安全修正值修正后得到的设计值及B′值汇总如表5、图7 和图8 所示。

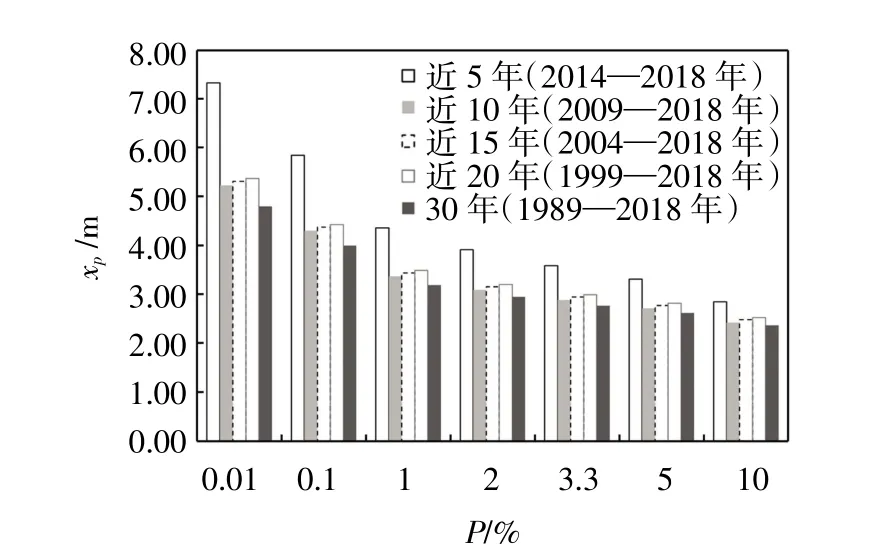
图7 不同样本容量的设计潮位xP 成果对比

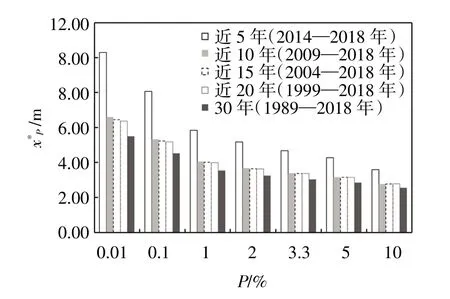
图8 不同样本容量的设计潮位x*P 成果对比

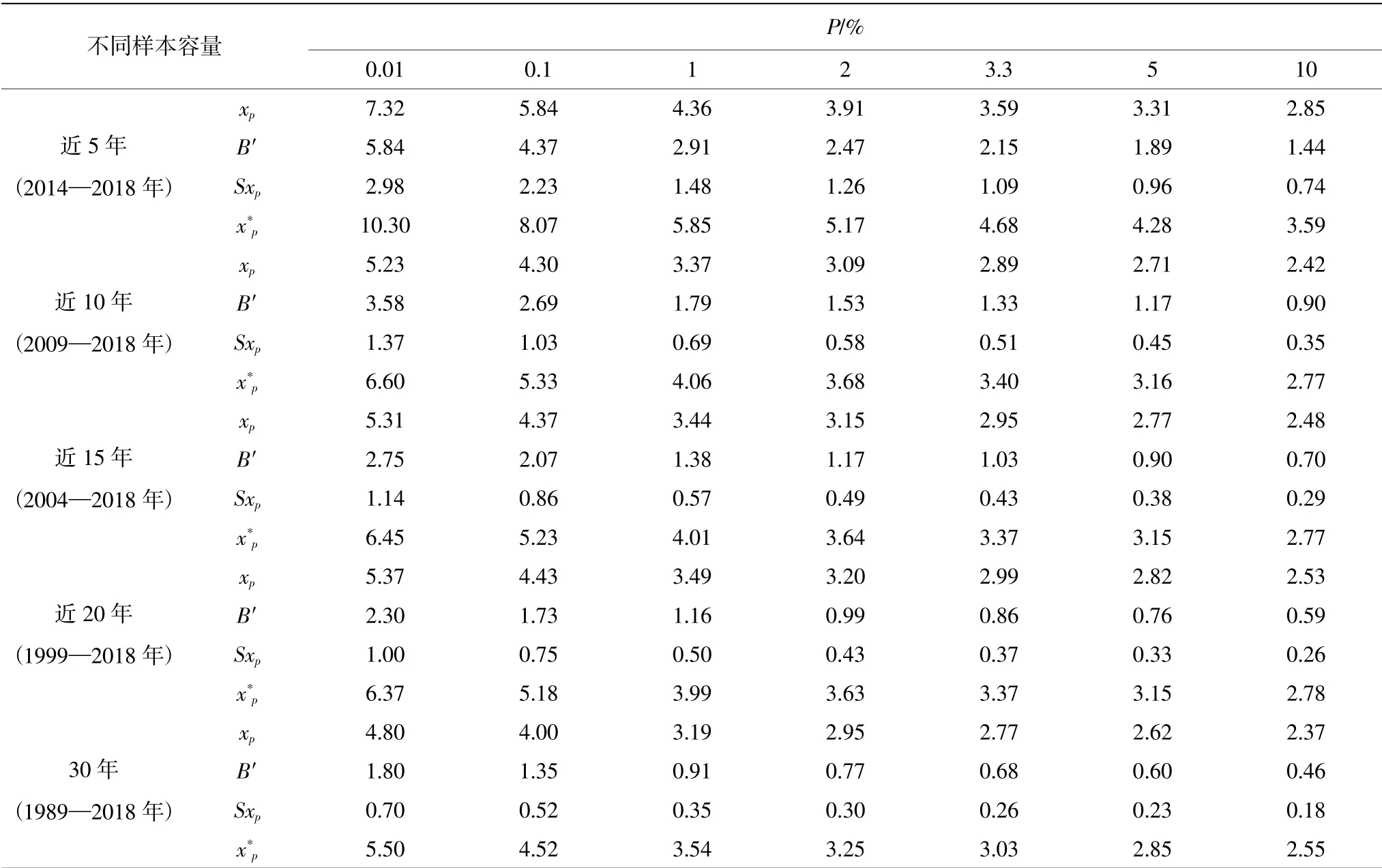
表5 不同样本容量对应的设计潮位成果汇总表

随着样本容量的增加，设计潮位值xP、 x*P大致呈现减小的趋势；近10 年、15 年、20 年的设计潮位值xP大小相当，不同样本容量的xP差异在0.11～0.14 m；以近30 年的xP为基础，频率越小，不同样本长度的xP差距越大，近5 年资料得到的设计值大了约20.3%～52.5%，近10 年、15 年、20 年的设计值大了约2.15%～11.9%。近10 年、15 年、20 年的设计潮位值x*P大小相当，不同样本容量的xP差异在-0.01～0.23 m；以近30 年的x*P为基础，频率越小，不同样本长度的x*P差距越大，近5 年资料得到的设计值大了约40.8%～87.3%，近10 年、15年、20 年的设计值大了约8.6%～20.0%。可见不同样本容量对设计值的影响较大，尤其是样本容量不足10时，引起的偏差达到了50%以上。

在不同样本容量时，不同频率的安全修正值SxP约为xP的7.1%～28.9%，约为x*P的7.6%～40.7%，且样本容量越小，SxP占xP、x*P的比例越大，具体如表6 所示；在使用近5 年的资料时，不同频率的安全修正值SxP约为xP的20.6%～28.9%，约为x*P的26.0%～40.7%；在使用近10 年的资料时，不同频率的安全修正值SxP约为xP的12.6%～20.8%，约为x*P的14.5%～26.2%；在使用近15 年的资料时，不同频率的安全修正值SxP约为xP的10.5%～17.7%，约为x*P的11.7%～21.5%；在使用近20 年的资料时，不同频率的安全修正值SxP约为xP的9.4%～15.7%，约为x*P的10.3%～18.6%。可见，样本容量越短，考虑安全修正系数修正抽样误差越有必要。对于《港口与航道水文规范》规定的不少于连续20 年的资料要求，本例的误差达到了10.3%～18.6%，可见考虑抽样误差十分必要。

表6 不同样本容量设计潮位相对误差汇总表

4 结 论

本文针对基于Gumbel 法进行参数估计的极值Ⅰ型分布，通过统计试验，研究绘制了安全修正值系数B 值的诺模图及考虑样本容量的B′值的诺模图，与多种方法参数估计的Pearson-Ⅲ型的B 值诺模图对比分析，并以某潮位站设计最高潮位计算为例加以验证，得到下列结论。

（1）海港工程设计与结构抗风设计中，常采用极值Ⅰ型分布推求稀遇频率的极端高水位、极端低水位、设计波要素和设计最大风速。本文基于现行技术标准推荐的Gumbel 参数估计方法进行统计试验，证明样本容量过小引起设计值的抽样误差不容忽视。

（2）极值Ⅰ型分布的安全修正值系数B 值与离差系数无关，为频率P、样本容量n 的函数，可采用本文统计试验得出的B 值或B′值诺模图近似估计该分布设计值的抽样误差。

（3）根据丛树铮等、刘攀等[7-8]的研究，对Pearson-Ⅲ型分布，在CS较小时，样本容量n 对B值的影响较小，可忽略n 对B 值的影响。然而，根据本文统计试验及实例分析，对于极值Ⅰ型分布，样本容量n 对B 值进而对极端水位设计值的影响相对显著，不宜忽略。

（4）本文提出的基于Gumbel 法参数估计的极值Ⅰ型分布的设计安全修正系数B 值介于Pearson-Ⅲ型分布CS=0.5～1.5 的B 值之间。

（5）本文实例验证了采用Gumbel 法进行极值Ⅰ型分布参数估计，获得的B 值、B′值诺模图可为海港工程设计极端高水位、极端低水位、设计波要素，以及结构荷载计算中的最大风速分析计算的设计值抽样误差估计提供可靠的依据，并可供相关设计标准修订时参考。