我国大学生成绩预测及专业分流引导实践探究——基于矩阵填充和回归模型的实证分析

韩 研,陈金如,柳宇菲

(1.南京师范大学党委巡察工作办公室,江苏 南京 210023)(2.南京师范大学数学科学学院,江苏 南京 210023)(3.太原师范学院数学系,山西 晋中 030619)

2019年10月8日,教育部印发了《关于深化本科教育教学改革 全面提高人才培养质量的意见》(教高〔2019〕6号),明确提出深化专业供给侧改革,构建自主性、灵活性与规范性、稳定性相统一的专业设置管理体系. 起源于20世纪80年代初的大类招生基础上的专业分流制度,成为培养模式的一个主流方向. 大类招生基础上的专业分流制度是指高校将相同或相近学科门类的专业合并,按一个大类进行招生,学生在入校经过1-2年的通识教育和学科基础培养后再进行专业分流. 这样的制度既有利于学生志愿的满足,体现了以生为本,又有利于因材施教和复合型创新人才的培养. 但就实践而言,由于学生对其专业能力的自我评估缺乏明确认知,而高校专业分流研究又相对薄弱,大多还处于初步阶段,只是表面现象的描述,对其内涵及构成要素缺乏分析,缺乏系统的实证实践研究[1-2],特别是缺少可操作性的实施体系,导致专业分流以后学生专业学习难以实现预期效果,培养质量下滑.

近年来,随着高等教育的大众化和高校办学自主权的扩大,特别是新时期对人才培养规格的要求和学生主体意识的增强,专业分流问题又再次引起了人们的关注. 毋庸讳言,目前我国本科大类招生基础上的专业分流制度问题很多,原因复杂. 但是作为专业分流活动执行与调控主体的高校,引导学生实现理性选择专业、根据学业规划自主发展是其应尽之责,也是高校实现立德树人根本任务的前提和基础. 本文对专业分流引导的范式建构进行探索,纵观学生的成绩预测研究方法,主要集中于四大类方法:关联规则法[3]、决策树法[4]、线性回归法[5]、贝叶斯算法[6]. 实际上,矩阵填充法被广泛地应用到各个领域,其中,最著名的就是美国一家最大的网上在线影片租赁公司Netflix应用这种数学方法建立了消费者与喜欢影片之间的一种关系,从而研发出“Cinematch”影片推荐系统,其推荐的准确率比以往的系统提高了10%.

本文采取矩阵填充这一类数学模型奠立对学生专业分流前的学力评估基础,继而以多元线性回归为工具,为专业分流的现实场域建构范式. 下文以某普通师范院校的小学数学教育、小学语文教育、小学英语教育3个专业的分流引导作为样本说明,所有数据及处理流程来自本研究实验的真实采集.

1 数据处理

以下为招生信息系统和教务管理系统中提取出研究所需要的初始数据样本集. 采集到的原始数据是关于此院校小学教育3个专业从一年级到三年级的文科类学生共188条记录,有效记录为187条,包括高考各科及专业基础课程共38门课程的成绩. 除成绩之外,数据还包括通过问卷调查得到的学生对自身数学、语文、英语发展的一个评估. 评估层次分为好、一般、差3个等级. 对于定类数据进行数字化处理,“好”“一般”“差”分别赋值为“3”“2”“1”. 如表1所示.

表1 原始数据结构Table 1 Raw data structure

为了数据的统一化,对成绩进行了百分制的归一化处理,使得所有的成绩分数取值范围处于[0,100]区间内. 部分数据如表2所示.

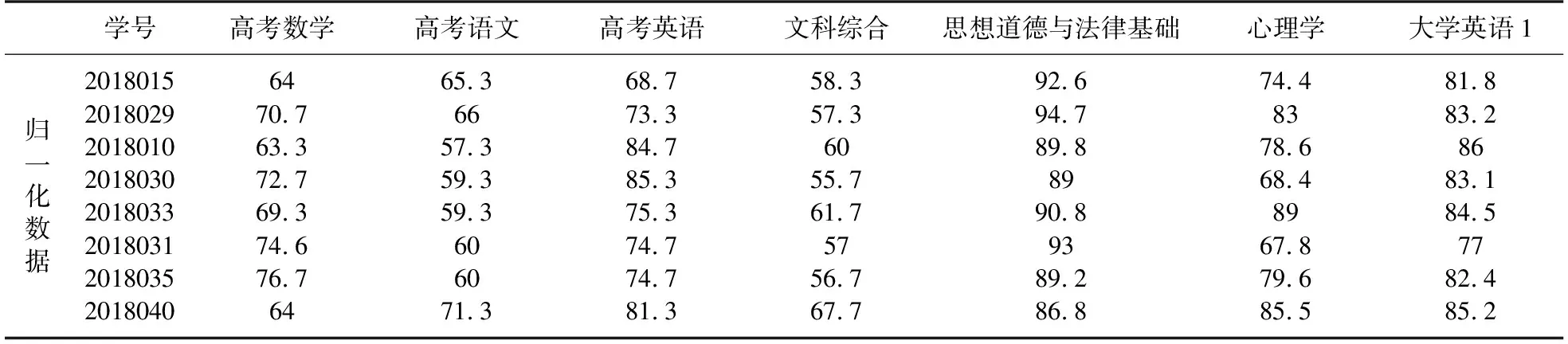
表2 部分原始课程成绩等级划分前数据Table 2 Part of the original course grades before classification data

2 矩阵填充模型的成绩等级预测

首先,将收集到的数据整理成矩阵的形式,每一行代表每个学生的各门课程成绩,未知成绩视为0.

其次,考虑到矩阵填充问题就是对于一个部分元素缺失的低秩数据矩阵M(矩阵M中所有已知的元素的下标集合用Ω表示),保证M矩阵中已有元素不变的情况下,准确填充缺失元素的方法.其数学表达式可描述如下:

min rank(X)
s.t.PΩ(X)=PΩ(M).

(1)

其中X,M分别为优化变量和待填充矩阵. 优化模型(1)的实质就是将缺失的元素数据填充后使得矩阵的秩尽可能低,即优化矩阵结构. 在此方案中,引导学生专业分流只需要对学生的成绩进行等级划分,从而满足矩阵填充这一数学方法的应用条件,也使得专业引导更有普适意义.

去除原始数据集中通常包含的学生姓名等冗余信息,剩余的数据构成一个187×38的矩阵A.对于成绩数据A,利用Matlab程序语言实现其等级划分. 其中,第一等级(90-100分)对应值为5;第二等级(80-89分)对应值为4;第三等级(70-79分)对应值为3;第四等级(60-69分)对应值为2;第五等级(0-59分)对应值为1. 为了更加清晰地展示成绩等级划分的结果,列举部分数据如表3所示.

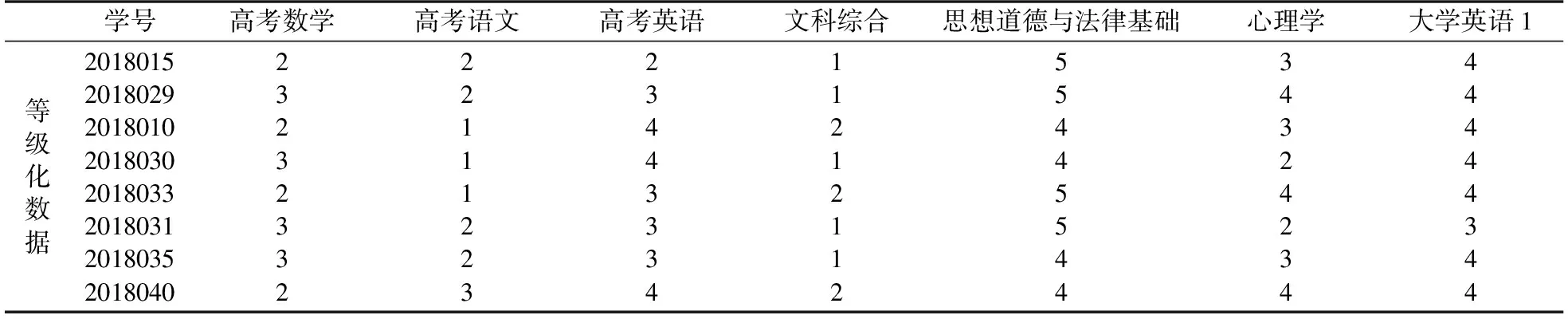
表3 部分课程成绩等级划分后数据Table 3 Data after grade division of some courses

最后,矩阵填充在图像恢复、系统识别等领域发挥着重要的作用[7]. 目前针对矩阵填充问题已有很多有效算法:内点算法、奇异值阈值算法、正交秩1矩阵跟踪法等. 本文所使用的算法是奇异值阈值算法[8],具体步骤如下:

第一步:给定下标集合Ω,样本元素PΩ(M),参数τ,步长δ,误差ε,给定初始矩阵Y0=δPΩ(M),k=0;

第二步:矩阵Yk的奇异值分解:

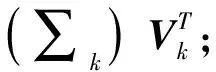
第三步:若

‖PΩ(Xk+1-M)‖F/‖PΩ(M)‖F≤ε,

停机;否则,转第四步;

第四步:Yk+1=PΩ(Yk)+δPΩ(M-Xk+1).

得到未知课程成绩等级状态,由于数据庞大,现以8名一年级学生6门课程预测成绩等级为例进行展示. 如表4所示.

表4 部分预测成绩等级Table 4 Part of the prediction grade

3 线性回归模型的专业分流

回归分析是数理统计中最基本也是最重要的方法之一,它通过回归建立模型处理变量之间存在的关系问题,应用数学模型将这种关系表达出来. 当变量之间的关系式是线性的则称为线性回归模型.

从监督学习角度来讲,每个实例都是在学习器中输入一个对象,得到一个期望的输出,这些实例的数据构成一个训练集,这个样本的形式是属性向量. 通常,给定了样本的向量形式之后,选择合适的假设函数进行分类. 在这些假设函数中,线性函数有着突出的特点:最简单,最易理解. 因此解决这种分类问题最常用的方法是线性回归. 其本质就是寻找一个线性函数

f(x)=〈w·x〉+b,

(2)

使其能够拟合一个给定的训练点集S={(xi,yi)}的误差最小,其中xi∈X⊆Rn,yi∈Y⊆R.

求解模型(2)最常用且有效的方法是最小二乘法.最小二乘法是以偏离数据的误差平方和(损失)最小为目标,根据这个目标来选择参数(w,b),其中

被称为损失函数.其具体计算方法如下:

通过对损失函数的参数(w,b)分别求偏导,并且令所有的偏导数为0,即,

求解上述方程可得(w,b),从而求得线性回归函数. 如果系数矩阵是奇异的,则可以使用伪逆. 从上面可知,应用线性回归进行预测主要步骤如下:

第一步:提取实验数据,组成训练样本集;

第二步:利用二次规划对训练样本求解最优化问题,从而求得最优的预测参数;

第三步:利用新的函数关系进行分类预测.

利用学生38门课程的等级成绩及自身对数学、语文、英语发展的评估数据分别对数学、语文、英语专业发展趋势建立线性回归模型,其中成绩及评估数据作为训练集. 3个专业的回归模型如图1所示.

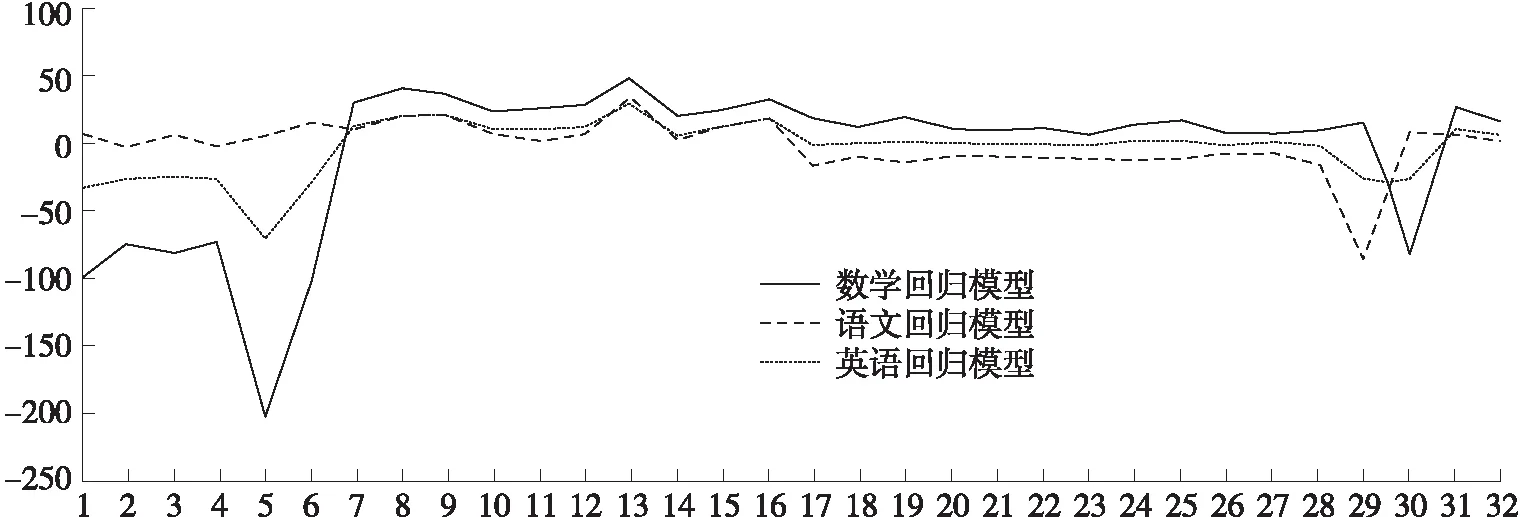
图1 数学、语文、英语专业发展趋势预测图Fig.1 Forecast chart of the development trend of mathematics,Chinese and English majors

表5 数学、语文、英语专业发展能力预测Table 5 Prediction of mathematics,Chinese and Englishmajor development ability

根据这3个模型及学习成绩计算出学生在每个专业发展方面能力的预测数据,即预测学生的数学、语文、英语专业发展趋势,从而确定合理的专业引导方向. 以学号为2018040同学为例,其数学、语文、英语专业发展能力预测数据如表5所示.

由表5可得,这位同学英语专业发展趋势最好,建议其选择小学英语教育专业. 通过调查,该同学也偏向选择小学英语教育专业.

4 专业分流引导方案设计

利用教育数据挖掘技术,通过数据驱动的方式构建学生专业分流引导方案. 具体来讲,基于矩阵填充和线性回归的专业分流引导方案步骤如下:

第一步,收集、整理数据. 收集学生的高考成绩、已有的基础课成绩;之后,将收集的数据整理成矩阵的形式,每一行代表每个学生的各门功课的成绩,未知课程成绩视为0.

第二步,成绩等级划分. 第一等级(杰出):90-100分;第二等级(优秀):80-89分;第三等级(良好):70-79分;第四等级(合格):60-69分;第五等级(不合格):0-59分. 根据成绩划分,学生成绩数据矩阵转化为等级划分之后的数据矩阵.

第三步,成绩预测. 针对上述的矩阵,利用矩阵填充模型及奇异值阈值算法进行学生成绩预测. 矩阵填充所得到的结果就是每个同学每门课程的成绩,即未知课程将根据此数学方法预测其成绩等级状态.

第四步,专业分类. 利用上述数据及学生自评的专业能力排名数据建立针对专业的线性回归模型. 利用学生的成绩,通过模型给出学生每个专业的发展趋势数据,并根据此数据引导学生进行专业分流.

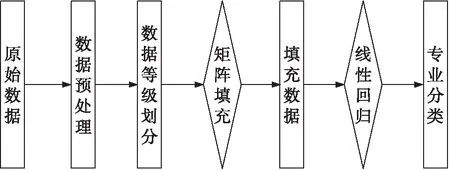
图2 流程图Fig.2 Flow chart

在此方案中,第二步进行成绩等级划分的原因:首先,引导学生专业分流只需要了解学生在哪个专业能够学到什么程度,不需要知道具体的分数,这样等级划分对于专业引导更有实际意义. 其次,矩阵填充问题的模型(1)的目标函数要求是矩阵的秩最小,也就是说要求数据矩阵是低秩矩阵,对学习成绩进行等级划分满足这一数学方法使用的条件,这样才能利用此方法解决成绩预测问题. 为了更好地展示专业分流引导方案,绘制流程图2.

利用我们提出的方案对一年级70名学生都进行了专业发展能力预测,其预测的专业分流情况部分数据如表6所示.

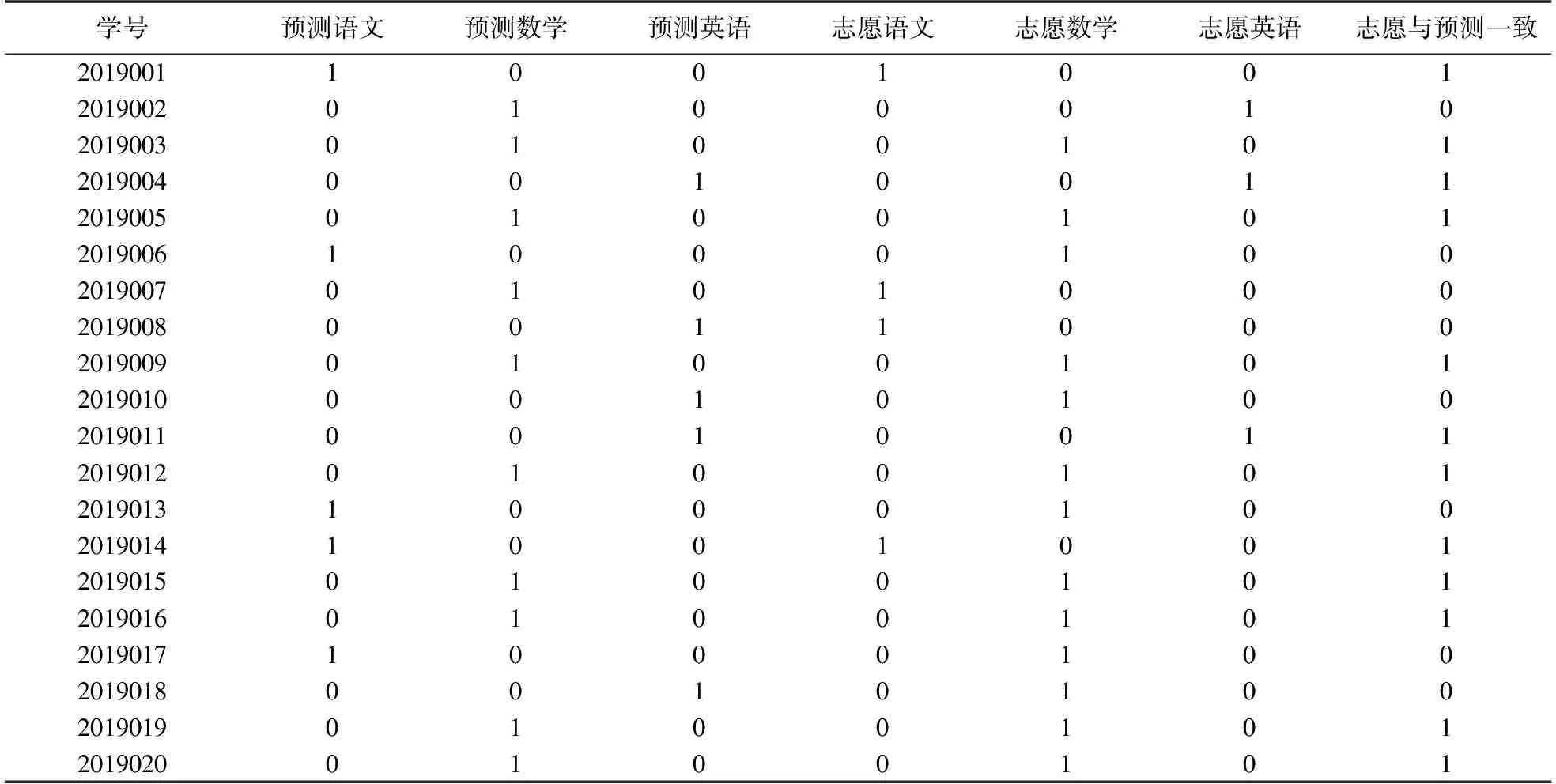
表6 部分一年级同学专业分流情况Table 6 Part of the first grade students major diversion situation

表7 数学、语文、英语预测与志愿人数Table 7 Mathematics,Chinese,English forecastand the number of volunteers

根据表6预测数据,从专业发展能力角度考虑,有15名学生适合选择小学数学教育专业,30名学生适合选择小学语文教育专业,25名学生适合专业小学英语教育专业. 结合之前问卷调查得到的学生对自身语文、英语、英语发展的一个评估得到表7.

由图3(a)可知,各专业预测人数与学生自主志愿人数基本相同.

由图3(b)可知,文科生更倾向于选择小学教育语文专业方向.

由图3(c)可知,适合小学数学教育专业的人较少,这与文科专业学生的学力分布特点一致,也是对本方案科学性的佐证. 在接受调研的70名学生中有49名学生自身目标意愿与方案推荐专业一致,一致性为69%,与科学预测及本人自我认知比例相当.

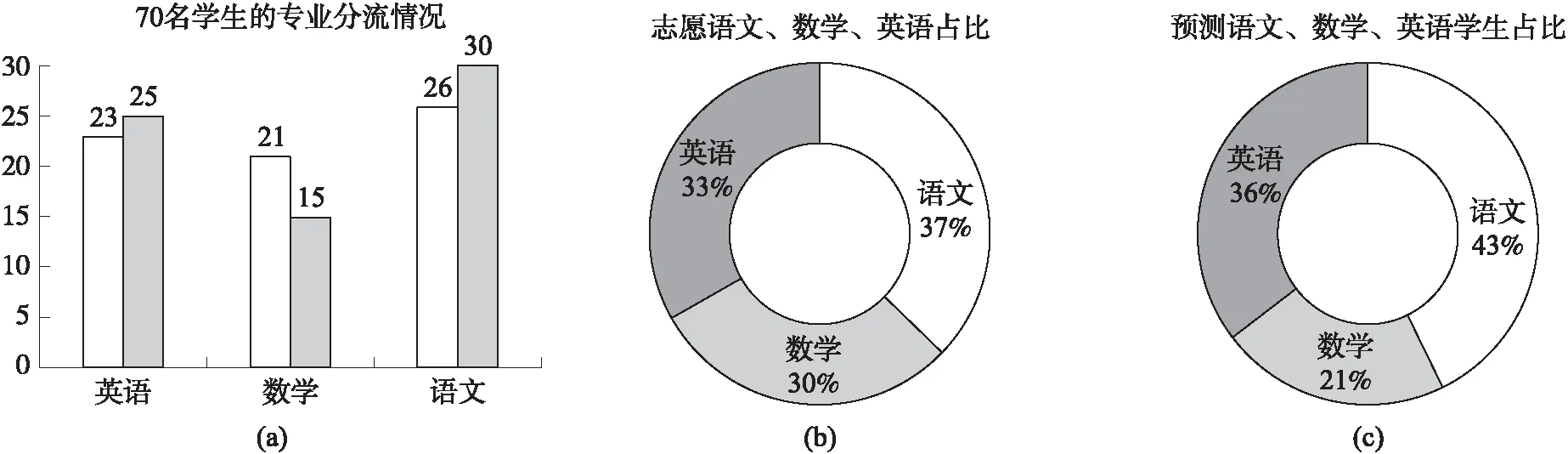
图3 各专业分流情况统计图Fig.3 Chart of majors partition

5 结论

高校专业分流表面是学生专业选择的个体行为,但实则是涉及到珍惜教育资源,实现立德树人,培养合格人才的模式问题. 面对这一困惑,我们不断进行高考制度改革,大学教育教学制度改革,在某种程度已有所改进,但仍然缺乏科学有效的具有可操作性的方法. 高校专业分流引导方案试图解决这一问题.

首先,受教育个体专业成绩预测可以通过数据化工具加以呈现. 上述个案研究结果和实践验证表明,充分利用大数据的特征规律,通过矩阵填充、线性回归的数学方法可以作为方法论得出科学合理的模型范式. 即通过收集学生的高考成绩及大学已有的基础课成绩,进行成绩等级划分,采用矩阵填充的方法,预测学生未知课程的成绩等级,在此基础上再采用线性回归法进行专业分类. 为了显示此方案的有效性和可行性,对70名学生进行了专业发展能力测试. 我们方案的分类结果与测试结果一致性可达70%左右. 这一方法,利用大数据资源,从不同视角采用数学分析法进行初步探索,为解决长期困扰我们的专业分流问题提供参考方案,避免了专业分流过程中出现的随意性、主观性、盲目性,丰富了专业分流方案的相关理论.

其次,成绩预测结果有利于高校专业分流引导实践,实现精准对标、因材施教. 高校专业分流引导方案针对目前高校管理和教育教学中的实际问题,从实践中来,又回到实践中进行检验、完善、丰富. 高校和教师作为专业分流方案主要实施者,一方面要把专业分流纳入招生制度改革、教育教学管理制度改革的范畴之内,以学生为本,关心学生的专业取向、专业成长、专业发展,克服传统模式弊端,突破专业分流环节的瓶颈,提升培养人才质量;另一方面,要面向学生个体,结合影响专业分流的因素,包括学习兴趣、专业认知、个人理想、教育背景、家庭环境、素质能力、国家政策、社会需求、经济待遇、就业机会、发展前程等综合研判,有的放矢,对症下药,对每个学生提出富有建设性的建议,帮助学生更好地规划学业生涯,提高高校本科教学培养质量.