基于微控制单元的彩色图像加密无线通信方案

贾晓霞,邢进生

(1.太原学院计算机科学与技术系,山西 太原 030000)(2.山西师范大学数学与计算机科学学院,山西 临汾 041081)

随着智能化设备、通信技术和互联网协议的技术进步,使用电子设备或嵌入系统ES,通过公共信道交换私密信息的服务和应用也呈指数增长[1]. 预计到2025年,使用嵌入系统的物联网(internet of things,IoT)设备全球数量将达到1 000亿台. 然而,威胁通信系统信息安全的攻击手段也在不断进化,必须确保信息传输的安全性[2]. 经典加密方案,例如数据加密标准(data encryption standard,DES),高级加密标准(advanced encryption standard,AES),国际数据加密算法(international data encryption algorithm,IDEA)等,在文本加密时性能较强,但由于数字图像加密中要区分的特征涉及的数据容量大,原始像素冗余性高,邻近像素关联性强,这些经典方案在数字图像加密中不能提供令人满意的安全性[3]. 且计算时间长,能耗高,不适用于数字图像的快速通信或实时加密[4].

混沌加密被视为保护机密信息的最安全方法之一,有着许多优秀属性,包括对初始条件的高敏感性和依赖性、行为不可预测性、遍历性、随机性、拓扑复杂性、对安全通信的高度适应性等[5]. 混沌映射已被广泛应用到数字图像加密中,与连续时间混沌系统相比,其运算量很小,需要的硬件资源也更少[6]. 经典混沌映射方法包括Henon、Tinkerbell、Chen和Logistic映射等. 当前,随着入侵手段越来越成熟,安全问题也逐渐复杂,这些方法的安全性已经不能满足通信要求[7]. 有必要开发新的嵌入式加密系统,提高安全性和效率[8].

文献[9]提出了基于Josephus问题和过滤扩散的图像加密方案,但其中至少需要两个加密轮,造成加密效率较低. 文献[10]提出了用于实时图像加密的一维混沌映射方案,该方案加密速度较快,能够满足实时处理要求,但该加密方案的随机性不足,容易被破解. 文献[11]提出了基于混沌logsitic映射,结合Haar小波变换和AES的图像加密方法. 文献[12]提出了基于DNA编码和超混沌算法的图像加密方案,利用SHA-3算法计算明文图像哈希值作为超混沌系统初始值并进行DNA序列运算,然后利用超混沌系统进行图像置乱. 文献[13]提出了超混沌系统与AES结合的图像加密算法,通过混沌序列产生每轮加密中的S盒和轮密钥,改善了密钥随机性. 文献[14]提出的图像加密技术中结合了4种不同加密算法(DNA-RSA-DES-Chebyshev,DRDC). 但对于嵌入式系统或MCU来说,这些算法的计算负荷过大.

本文针对无线链路上的图像传输安全问题,设计了适用于低功耗设备的图像加密方案,使用MCU构建基于混沌映射的PRNG,加强了输入混沌序列的随机性,仅利用单个混沌映射算法就能够确保彩色图像的传输安全性,显著提高了处理速度. 大量安全分析证明所提方案具有密钥空间大,加密图像的像素相关性低,传输过程中保密信息无损失的优点,且处理速度显著优于AES等经典加密方法.

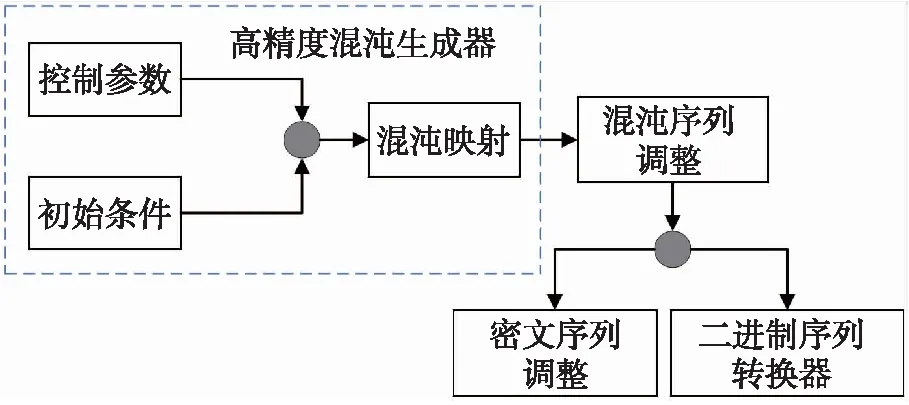
图1 伪随机序列生成器Fig.1 Pseudo random sequence generator

1 基于混沌映射的密码系统

所提密码系统基于简单的对称密钥流编码[15],通过加密运算,利用密文字符串S={s1,s2,…,sn}对包含n个元素的消息M={m1,m2,…,mn}进行加密.为提高加密方法安全性,S编码的序列中必须包含唯一随机元素,利用混沌映射,设计了混沌发生器,以生成用于密文序列的伪随机序列X,Y,…,Z.本文实施的伪随机序列生成器如图1所示.

1.1 系统实施

在SOC Raspberry Pi 3上实施伪随机序列生成系统,其中包含3个基本实体:控制参数,初始条件和混沌映射.混沌映射相关的每个状态X={x0,x1,…,xn},…,Z={z0,z1,…,zn},对应于一个浮点元素的伪随机序列.

混沌映射的动态行为具有离散性和复杂性,适合在加密算法中实施.本文在所提密码系统中测试了 3个经典混沌算法,即Henon、Tinkerbell和Chen混沌映射[16].

Henon混沌映射可表示为:

(1)

其动态性取决于两个参数,x0=0.10,y0=0.15.

Tinkerbell混沌映射可表示为:

(2)

式中,a=0.9,b=-0.6013,c=2,d=0.5.

Chen超混沌映射可表示为:

(3)

式中,a=1.95,b=1,初始条件x0=0.025,y0=0.025.

1.2 位伪随机序列生成器

基于图1,且仅考虑混沌映射的输出状态X,通过所提高精度混沌发生器实体生成预定义数值精度的元素,其后通过“混沌序列调整”得到整数元素序列D={d0,d1,…,dk-1}.将得到的D序列输入二进制序列转换器,得到序列B={{b0,0,b0,1,…,b0,nb},{b1,0,b1,1,…,b1,nb},…,{bk-1,0,bk-1,1,…,bk-1,nb}},如图2所示.将nd定义为每个元素dn包含的位数(通过将元素转换为位序列得到),将高精度混沌序列的每个xn数据与1×10np相乘,以得到整数dn,代表最大nd=np+1的整数位数.子实体“二进制序列转换器”中的每个元素得出的位序列的最大长度为nb=log2(1×10nd)+1(包括符号位),其中n为十进制整数.

1.3 数字图像加密

使用所提密码系统进行数字图像加密的程序如图3所示. 针对数字图像加密,遵循IEEE 754标准,利用32位浮点计算得到混沌序列,再将其映射为8位二进制序列. 所提加密程序中,将混沌序列与常数 1×106相乘,以得到32位整数,其后使用mod 255函数将其转换为8位格式的二进制序列. 使用二进制序列,通过XOR操作对数字图像进行加密,由此提升混沌信号的随机性.

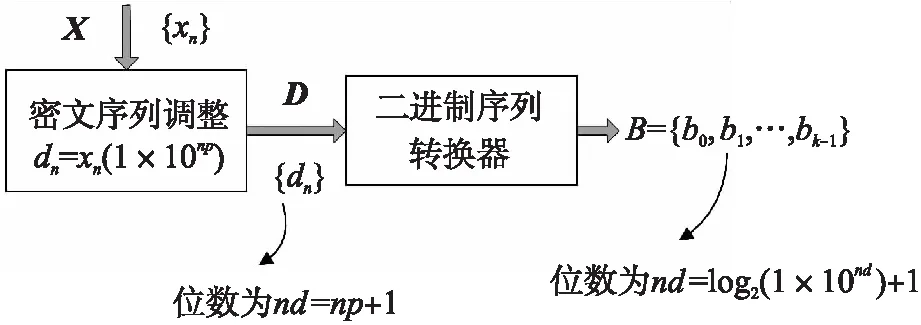
图2 生成位伪随机序列的程序Fig.2 Program for generating bit pseudo-random sequence

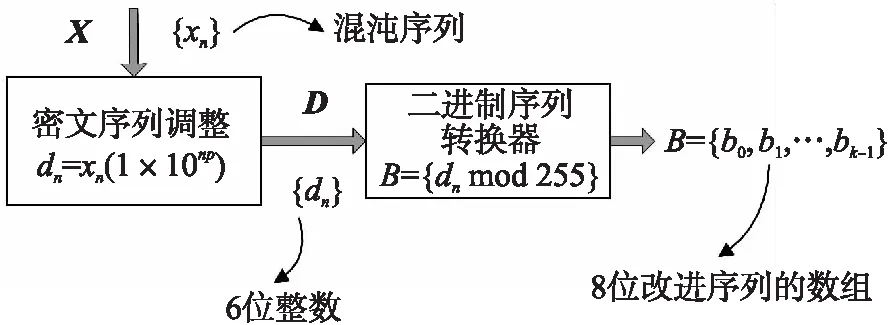
图3 混沌序列改进方法Fig.3 Improved method of chaotic sequence

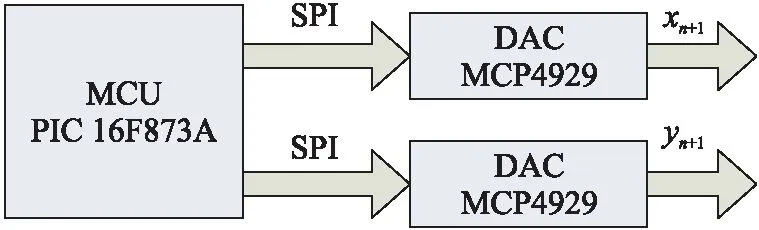
图4 PRNG框图Fig.4 Block diagram of PRNG

1.4 基于MCU的PRNG

基于MCU PIC 16F873A的电路区块方案如图4所示,以生成混沌序列. MCU执行混沌映射以生成伪随机数(PRNG). 为观察并验证生成混沌序列的行为,通过DAC MCP4929对序列进行数模转换.

2 加密图像的无线通信方案

当前的芯片系统(SOC)通常包含作为实时中央处理单元的微处理器或微控制器,RAM和FLASH存储器,以及一些通信端口,例如RS-232、USB、蓝牙,WiFi等. 其中嵌入了时钟振荡器,用于内部操作和能量子系统的同步化. 为保障运行和信息管理,应使用通信协议防火墙,通过无线信道(例如Zigbee,Wifi等)发送信息. 所提方案的功能模块如图5所示.

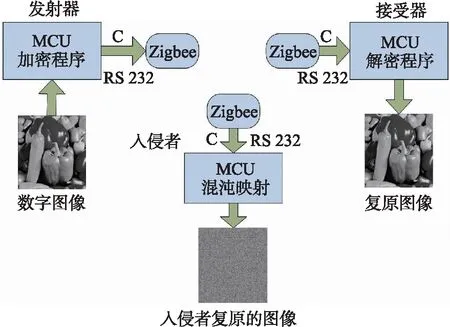
图5 本文方案的各个模块Fig.5 Each module of this scheme

使用RF发射器(例如ZigBee或Wifi模块),通过RS-232端口发送嵌入式加密系统的输出. 在接收器中执行与加密相反的操作. 通过Zigbee标准将3个MCU PIC16F877A连接在一起,分别代表M2M方案中的发射器、接收器和入侵者. 使用XCTU软件完成Zigbee发射器的设置. 无线通信参数配置为:Baud=115200,FlowControl=NONE,DataBits=8,Parity=NONE,StopBits=1. 调制解调器参数配置为:PAN ID,Destination Address High,Destination Address Low(Serial Number Low). 假设入侵者可连接到Zigbee信道,并尝试提取保密信息. 要加密数字图像时,通过MCU的RS-232/USB串口接收. 在接收器侧,执行与加密相反程序,恢复通过RS-232/USB串口发送到PC的保密信息.

为实施所提方案,使用以C语言编码的中央设备MCU PIC 16F873A,执行混沌映射,生成PRNG. 其后,MCU使用本文所提密码系统,通过XOR操作对数字图像进行加密.

本文图像加密程序中,将混沌序列与常数1×106相乘,以得到32位整数,其后使用mod 255函数将其转换为8位格式的二进制序列. 使用二进制序列,通过XOR操作对数字图像进行加密,由此提升混沌信号的随机性. 如下算法给出了通过MCU对保密信息进行加密和传输的主要过程. 在接收器中执行相反操作.

算法:本文无线通信中的图像加密算法

输入:混沌映射的条件、变量,以及无线通信参数和调制解调器参数;

输出:Zigbee信道发送出的加密信息;

1 初始化 混沌映射的条件和变量(针对不同的混沌映射会有不同的条件初始化,见式(1)、式(2)、式(3);

2 初始化 参数(无线通信参数和调制解调器参数配置);

3 计算混沌序列;

4 通过(1×106)调整混沌序列,得到xadj;

5 使用mod(xadj,255)改进混沌数据,并转换为二进制;

6 读取数字图像;

7 在混沌二进制数据和数字图像的每个像素之间执行XOR操作;

8 通过Zigbee信道发送加密结果.

3 实验结果与分析

本节将通过安全分析,检验所提方案的稳健性、统计特征和安全性等.

3.1 密钥空间

表1 密钥空间大小Table 1 Space size of key

密钥空间是在加密或解密程序中使用的不同密钥总数量. 有效安全的密码系统的密钥空间应足够大,以抵御蛮力攻击. 所提密码系统的密钥包含两部分:(1)初始条件;(2)混沌映射参数. PRNG的密钥必须包含超过2 100个可能密钥,以抵御穷举攻击. 本文使用IEEE 754标准的单精度和双精度浮点数计算分别实施了3个混沌映射,将混沌序列临时保存在32位和64位存储寄存器中. 所提嵌入式密码系统使用不同混沌映射时的密钥空间如表1所示. 从中可发现,所有混沌映射均满足最小密钥空间标准,证明本文方案可以抵御蛮力攻击.

3.2 统计检验

利用NIST SP800-22统计检验套件,应用到不同混沌映射生成的二进制序列的比较结果如表2所示. 所有测试中,序列流包含100个序列,序列流长度为1 000 000位. 测试中,使用的决策规则为1%水平,即α=0.01.若计算出的P值大于等于α,则可认为该序列是随机的,且置信度为99%. 否则,可认为该序列是非随机的,置信度为99%. 此外,若成功率大于0.96,则可认为该序列通过了NIST检验,证明该序列是随机序列. 表2中可发现,除了块内最长连续“1”测试之外,应用本文方案的混沌序列成功通过其他NIST测试.

3.3 直方图分析

为执行数字图像直方图上的统计分析测试,使用Lena 512×512灰度图像. 选择改进Tinkerbell混沌映射的x1状态执行信息加密,并给出直方图分析. 图6(a)是原始图像,相应直方图如图6(d)所示. 加密图像如图6(b)所示,可发现该图像对于入侵者毫无价值. 图6(e)给出了加密图像的相应直方图,从中可发现信息在0到255灰度等级的整个范围上分布,即以随机数据的形式均匀分布,由此证明所提密码系统可以很好地抵御统计攻击. Lena的恢复图像如图6(c)所示,可发现与原始图像相同,证明在加密和无线通信过程中没有信息损失. 最后,恢复图像的直方图如图6(f)所示,从中可发现与图6(d)的原始图像直方图基本相同,这证明了没有保密信息损失.

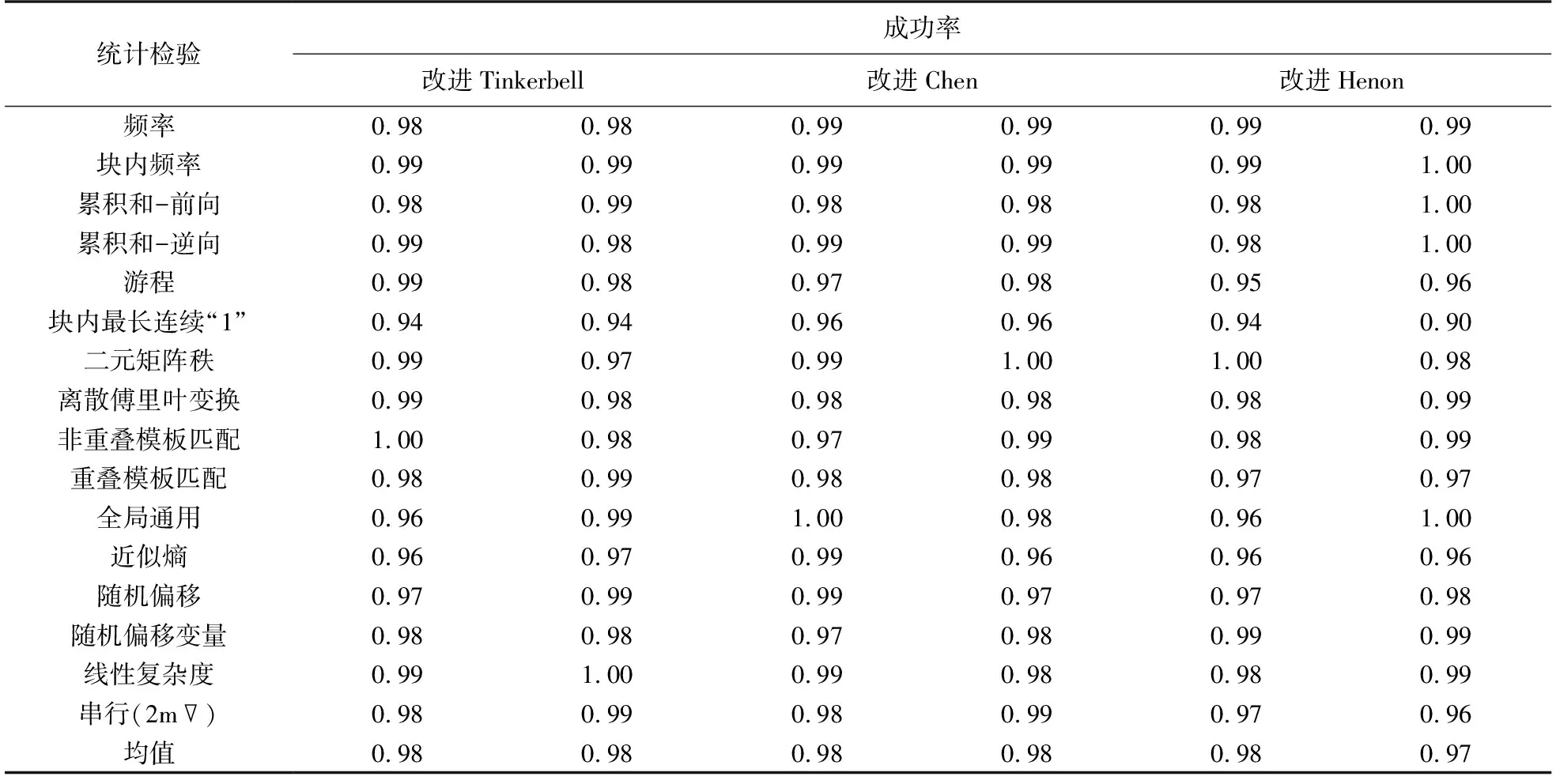
表2 所提方案的NIST统计分析结果Table 2 NIST statistical analysis results of the proposed scheme

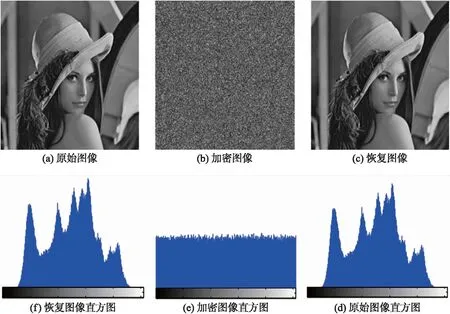
图6 加密数字图像Lena的直方图分析Fig.6 Histogram analysis of encrypted digital image lena

3.4 相邻像素相关性分析

通过加密图像中相邻像素的相关性检验[17],分析加密程序设计的扩散和混淆性能. 随机选择要分析的数字图像(原始或加密)的5 000对像素(xi,yi),然后计算相应的相关系数rxy:

(4)

式中,

(5)

式中,cov(x,y)为协方差,D(x)为方差,x和y表示数字图像中灰度等级的标度值.使用以下离散形式:

(6)

(7)

式中,E(x)为像素平均灰度等级.

原始Lena图像和通过改进Henon混沌映射的x1状态进行加密的图像的5 000对相邻像素在水平、垂直和对角方向的相关性分布如图7所示. 其中,图7(a)是原始图像的相邻像素相关性分布图,可发现相邻像素是高度相关的,像素值与邻近像素值接近,且大多集中在对角线两边的区域. 图7(b)给出了加密图像的像素相关性,可发现邻近像素的相关性完全不同,无明显像素堆积情况或明显的空白区域,平面上可观察到非常大的离散性.

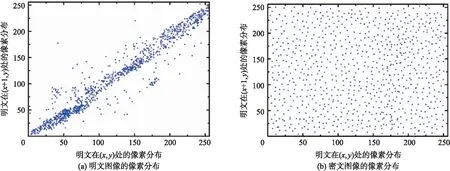
图7 原始图像和加密图像中的邻近像素相关性Fig.7 Correlation between adjacent pixels in original image and encrypted image

相关系数rxy值如表3所示,可发现原始图像相关系数接近1,即相邻像素非常相似. 加密图像的理想相关系数应等于0,可发现大部分情况下相关系数接近0. S-box、AES和DRDC与0差距较大,证明这些方法不能很好地完成图像加密.

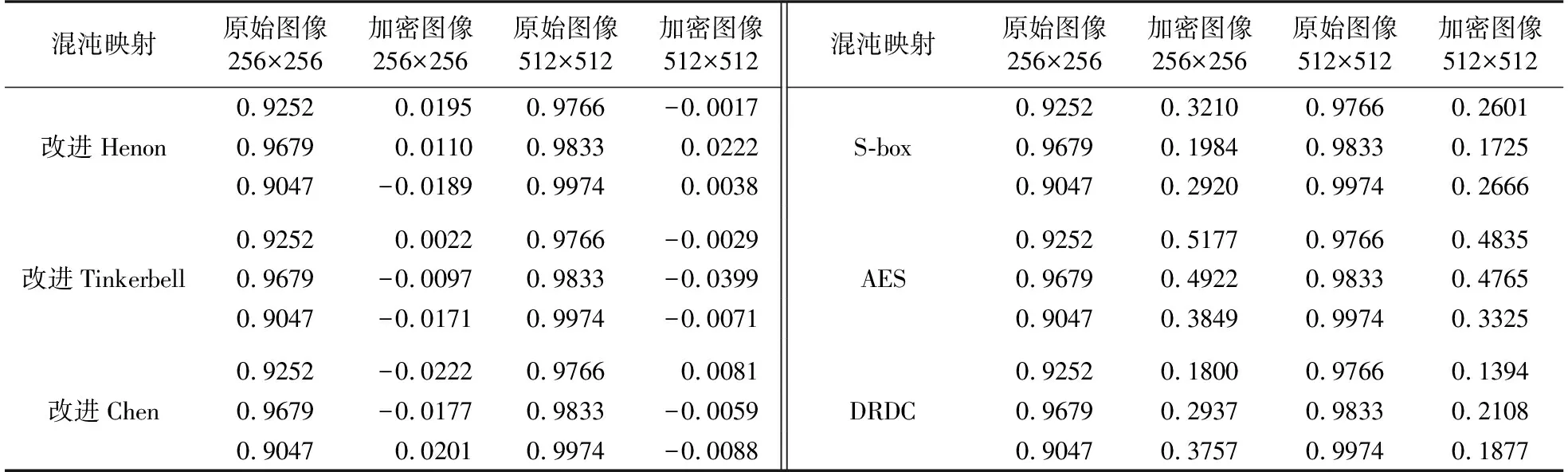
表3 邻近像素的相关系数Table 3 Correlation cofficient of adjacent pixels

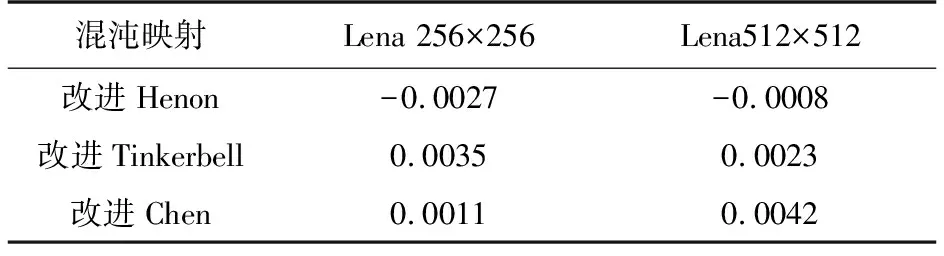
表4 相关系数rTable 4 Correlation coefficient r

原始图像和加密图像之间得到的相关系数r如表4所示.可发现大部分情况下,相关系数r非常接近0,表明原始图像和加密图像之间不相似.这也表明所提方法适用于任何图像大小.

3.5 信息熵分析

信息熵是测量数据随机性的指标[18],也用于评估加密安全性,计算如下:

(8)

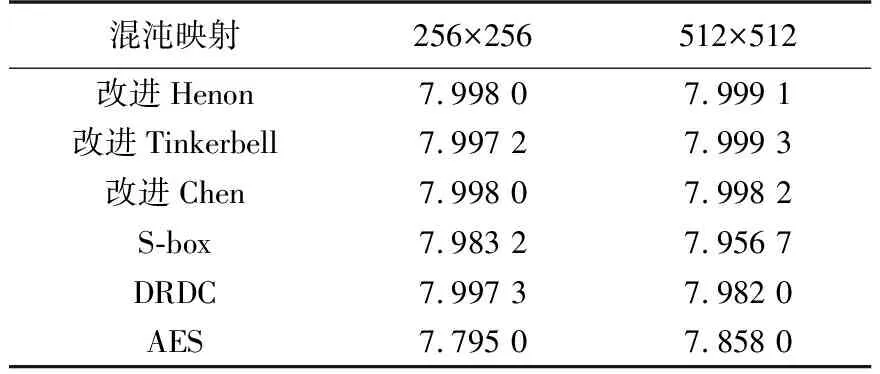
表5 密文图像的熵值比较Table 5 Entropy comparison of ciphertext images

式中,P(si)表示si符号的概率. 对于以相同概率给出2N个符号的纯随机源,熵H(s)=N,即对于完全随机像素组成的8位图像,熵的理想值为H(s)=8bit.对于数字图像加密,理想熵值为8.加密系统发出的符号(密文)的熵值低于8,则存在一定程度的可预测性,存在安全隐患.使用8位格式Lena图像,使用的5个混沌映射与其他方法得出的熵值比较如表5所示.从中可发现,熵值不受图像大小影响,且各方法性能接近.此外,经典加密算法AES的熵值与8差距较大,有一定程度可预测性,存在风险.证明其不适用于图像加密.

3.6 NPCR差分攻击

为执行差分攻击,使用两个常用指标,NPCR和UACI.其用于测量整个加密布局中像素变化的影响.使用512×512的Lena灰度图像,接收器的加密密钥x1有着1-10的差异,得到两个有着细微差异的密文C1和C2.NPCR检验结果如表6所示,从中可发现,所提方案在使用3种混沌映射时,均通过了NPCR差分攻击检验.经典S盒和AES加密算法通过了NPCR检验,但DRDC加密算法未通过检验.证明本文方案有效改善了输入混沌序列的随机性,提高了加密图像的安全性.使用双浮点精度PRNG的处理速度为13.52Mbit/s,如表7所示,结果证明所提方案适用于现实应用和电信设备.

表6 NPCR检验结果Table 6 Test results of NPCR

表7 处理速度(Mbit/s)比较Table 7 Comparison of processing speed(Mbit/s)

4 结论

本文提出了无线链路上彩色图像实时加密传输方案,其中通过在MCU上实施的PRNG,提高了输入混沌序列的随机性,增强了无线信道上传输的彩色图像的安全性. 使用单个混沌映射方法和XOR操作完成图像加密,显著降低了计算量和处理时间,支持彩色图像在M2M链路上的实时通信. 在PIC微控制器上的仿真和实验结果表明,所提方案在使用不同的混沌映射算法时,均能够提供彩色图像加密所需的安全性,抵御各种已知攻击,顺利通过了 NPCR和UACI差分攻击检验,且处理速度能够满足M2M和IoT环境中低功耗设备的加密图像实时传输要求.