国家农业科技园区对区域农业经济增长的影响研究*

薛庆根，朱瑾

(扬州大学商学院，江苏扬州，225127)

0 引言

20世纪90年代，为应对全球激烈的农业产品竞争，我国在北京和上海建立了农业示范区，引进以色列、荷兰在农业生产方面的先进设施。2001年，我国正式开始第一批国家农业科技园区的试点工作，截至2020年12月，经科技部、农业农村部等6部门批准建设的九批国家农业科技园区共304个，其中274个国家农业科技园区已经通过验收。作为以技术创新为核心的新型农业发展模式，国家农业科技园区逐渐发展成为技术组装集成、科技成果转化及现代农业生产的示范载体。历经多年实践，园区在孵化培育、创新产出、集成示范方面的效益显著，创新监测报告显示，前八批建立的278个国家农业科技园区核心面积达92.58 hm2，园区入驻企业33 152家，引进新技术、新品种和新设施18 108个[1]。

新经济发展格局下，在注重二三产业提质增效的同时要进一步加强现代农业产业体系建设，通过不断优化农业产业结构、提升农业生产效率来提高农业供给质量。2020年中央一号文件指出，要强化科技在推进农业现代化建设中的作用，加强现代农业技术体系建设，扩大名特优农产品的覆盖范围，面向农业产业配置科技资源，加强国家农业科技园区等农业科技创新平台的建设。《国家农业科技园区发展规划(2018—2025)》同样指出，在经济高质量发展时期，必须以实施创新驱动发展战略和乡村振兴战略为引领，深入推进农业供给侧结构性改革，不断提高农业综合效益和竞争力。

纵观现有农业科技园区相关研究，大致可分为3类。一是对农业科技园区的发展绩效进行评价，艾洪娟等[2]基于企业带动、产业带动、技术引领、技术推广、企业孵化5个功能分析园区发展成效；谢玲红等[3]从农业、农村、农民3个层面构建指标并计算权重，结果显示国家农业园区在推动农业升级方面表现得更好。二是分析农业科技园区的创新能力，王秀芳等[4]、钱政成等[5]、霍明等[6]将创新投入、创新支撑、创新产出、创新绩效作为一级指标构建评价体系，分析农业科技园区的创新能力；夏岩磊[7-8]研究发现，相较于传统要素，创新要素对国家农业科技园区经济增长的影响更强，并且园区创新产出会受到地理差异的影响。三是分析农业科技园区的经济效益，此类研究相对较少。赵黎明等[9]运用CES模型研究发现，农业科技园区发挥着产业集聚作用；钱政成等[5]指出，国家农业科技园区通过农业科技成果转化、农业产业升级、农业科技人才培养等手段发挥了减贫作用；夏岩磊[10]指出，国家农业科技园区可通过极化和扩散效应形成所在区域的农业经济增长极。以上关于国家农业科技园区的研究大多局限于构建评价体系分析园区自身的发展绩效和创新能力，研究农业科技园区经济效益的文献较少，并且鲜有学者关注国家农业科技园区对园区外农业产业发展的影响。鉴于此，本文将探究国家农业科技园区与区域农业经济增长之间的关系，识别国家农业科技园区在农业经济增长中发挥的政策效应，为进一步加强国家农业科技园区的建设提供可靠的定量证据。

1 理论分析与研究假说

增长极理论认为，增长极在离心力的作用下，将增长的方向通过技术、组织、要素、信息等渠道向其周边地区扩散，从而使区域经济通过多层次的增长极在不同的点上带动经济增长。国家农业科技园区的建设初衷就是通过农业科技成果转化促进农业增长、农村发展、农民进步。在园区建设初期，地区政府会加大对园区的资金等要素的投入，随着地区国家农业科技园区经济实力不断增强，扩散和辐射效应便会发挥作用，园区将集聚的生产要素进一步投入到农业生产中，扩大农业生产规模，实现园区对农业经济增长的促进作用。

高新技术改造传统农业理论指出，要将高新技术渗透到生产的各个环节，从而使农业资料不断变革、农业劳动对象不断扩大、农业劳动者素质不断提高，形成全新的农业生产力系统[11]。国家农业科技园区是科技创新与成果转化的核心平台，园区通过自主研发新品种、新工艺和引进新的农业技术和生产方式两种途径不断提升科技创新水平，将高新技术融合到农业生产的各环节。一方面，新品种、新技术的应用能够提升农产品的核心竞争力；另一方面，新的生产方式、新工艺也将不断提升农业产业的生产效率。

基于上述理论，本文提出如下两个假说。

假说1：国家农业科技园区对区域农业经济增长具有显著的促进作用。

假说2：国家农业科技园区通过提升区域技术创新水平来促进农业经济增长，即技术创新是国家农业科技园区促进区域农业经济增长的路径之一。

2 数据来源与研究方法

2.1 样本选择和数据来源

我国于20世纪末提出建立农业科技园区的发展方案，并于2001年、2002年开始第一、二批国家农业科技园区的试点，之后分别在2011年、2012年、2013年、2015年2月和12月、2018年、2019年批准第三至第九批国家农业科技园区的建设工作。虽然前两批国家农业科技园区早在20世纪初就已建立，但科技部直到2009年才对这些园区进行验收，因此这一时期政府和地方对于国家农业科技园区的建设仍处于探索阶段。随着政策的不断完善，2010年以后国家农业科技园区进入良好发展阶段，园区建立的数量和发展质量都取得了巨大突破。因此，本文在进行样本筛选时剔除了前两批建设的国家农业科技园区，只保留第三至第七批建设并且已经通过科技部验收的国家农业科技园区。其次，实证分析部分的数据区间为2010—2019年，考虑到部分城市数据缺失严重，故只将全国22省的254个地级市纳入研究范围，删除自治区和三沙市样本。最后，对于拥有多家国家农业科技园区的地级市，只保留最先建立的园区样本，本文最终将114个地级市样本归入处理组。

实证分析部分选用的数据主要来源于各省、市的《统计年鉴》及《中国城市统计年鉴》，部分缺失数据通过查找地级市统计公报补齐。其中衡量区域技术创新水平的中介变量选取北京大学企业大数据研究中心公布的中国区域创新创业指数。

2.2 模型设定

本文将国家农业科技园区视为一项准自然实验，借鉴甘天琦[12]、王佳楠[13]在政策评价中使用的双重差分法，分析国家农业科技园区对区域农业经济增长的影响效应。双重差分法不仅能在很大程度上避免内生性问题，而且模型设置科学，能更加准确地估计政策效应，因此备受学者们青睐。本文的研究对象为国家农业科技园区，考虑到各地区的农业科技园区建设批次并不一致，因此借鉴Autor[14]的研究，构建多期双重差分模型，模型设定如下

yit=α0+α1didit+∑xit+γi+γt+εit

(1)

式中：i——城市；

t——年份；

yit——城市i在t年的农业经济增长情况；

didit——虚拟变量，如果城市i的农业科技园区在t年被批准为国家农业科技园区，则该年及以后赋值为1，反之为0；

xit——一组可能影响区域农业经济增长的控制变量；

γi、γt——城市、时间固定效应；

εit——随机扰动项。

本文重点关注式(1)中α1是否显著，若显著为正，则表明国家农业科技园区的建立对区域农业经济增长发挥了促进作用。

理论分析部分的假设2指出技术创新可能会在国家农业科技园区影响农业经济增长中发挥中介作用，因此在基准回归模型的基础上，进一步检验技术创新发挥的中介效应，本文基于逐步回归系数检验方法[15]，在式(1)的基础上构建递归模型

innovationit=λ0+λ1didit+∑xit+γi+γt+εit

(2)

yit=β0+β1didit+β2innovationit+∑xit+γi+γt+εit

(3)

式中：innovationit——城市i在t年的技术创新水平；

λ1——国家农业科技园区对地区技术创新水平的影响程度；

β1——加入中介变量后国家农业科技园区对区域农业经济增长的影响水平。

若回归模型中系数λ1、β2显著，且系数β1小于α1，则说明技术创新发挥了部分中介效应。

2.3 变量说明

2.3.1 被解释变量

已有研究中，部分学者选择农林牧渔业增加值或农民人均纯收入衡量农业经济增长水平，为消除价格变动带来的影响，本文借鉴王佳楠[13]、黄龙俊江[16]、邓翔[17]的研究，选取地级市农林牧渔年度总产值作为区域农业经济增长水平的代理变量，并取对数处理。

2.3.2 核心解释变量

本文的核心解释变量是国家农业科技园区，若该城市拥有国家农业科技园区并已经通过验收则进入处理组，组间虚拟变量为1，反之为0；该城市建立农业科技园区的当年及之后的时间虚拟变量均取值为1，其余为0；将组间虚拟变量和城市虚拟变量交乘后得到核心解释变量didit，本文重点关注系数α1。

2.3.3 控制变量

在控制变量的选择上借鉴庞金波[18]、李兆亮[19]的研究，选取主要农作物播种面积作为土地要素的代理变量，农作物播种面积的扩大能直接提升农业种植规模，从而促进区域农业经济增长。采用农林牧渔城镇从业人员衡量地区农业发展中的劳动力投入水平，随着农村劳动力的不断外溢，劳动力要素对农业经济增长的影响逐渐减弱。使用农业机械总动力、农用化肥施用折纯量衡量地区农机和化肥投入对农业经济的影响，农业机械和化肥的广泛使用能够提高农业的生产效率和产出水平，推动农业经济增长。最后将粮食总产值也纳入控制变量，粮食产值能够直接体现区域农业产出水平，进而影响区域的农业经济增长。以上变量除农林牧渔城镇从业人员外均进行对数处理。

2.3.4 中介变量

表1是主要变量的详细说明及描述性统计结果。

表1 主要变量说明Tab. 1 Description of main variables

考虑到地级市层面缺乏衡量农业技术创新水平的数据，因此本文选取北京大学企业大数据研究中心公布的中国区域创新创业指数作为区域技术创新水平的代理变量，该数据能客观反映地级市层面的技术创新水平。

3 实证结果

3.1 基准回归

本文通过双向固定效应检验国家农业科技园区对区域农业经济增长的净效应，表2模型(1)仅将农林牧渔总产值对数值作为被解释变量进行回归，回归结果在1%的水平上显著，表明国家农业科技园区对区域农业经济增长具有明显的提升作用，具体而言，建立国家农业科技园区的区域，其农林牧渔总产值会有4.7%的提升。在模型(2)～(5)中依次加入控制变量后回归结果依然十分显著，但是影响系数从0.047降至0.039。从控制变量的回归结果来看，农作物播种面积、农业机械总动力、粮食总产值的回归结果均在1%的水平上显著为正，而农林牧渔城镇从业人员与农用化肥施用折纯量的回归结果并不显著。科布道格拉斯生产函数认为增加土地要素的投入能直接增加产出，相较于传统的以人为主的农业生产活动，机械化种植、收割、加工的生产方式具备规模效应，在提高农业生产效率的同时降低了单位农产品的生产成本，从而提高商品的剩余价值。粮食产值能直接体现地区农业的产出水平和农业结构，农业产出水平越高，地区的农业经济增长水平越高。

表2 基准回归结果Tab. 2 Baseline regression results

3.2 平行趋势检验

从回归结果可知，国家农业科技园区对区域农业经济增长起到了显著的促进作用。但双重差分法的适用前提是满足平行趋势，即在建立国家农业科技园区前，实验组和对照组具有相同的变化趋势。国家农业科技园区从批准建设到完成验收通常要经历最低3年的建设周期，受政策制度、设施要素等的影响，处于不同时期的国家农业科技园区对农业经济发展发挥的效用水平可能具有差异。平行动态趋势检验图如图1所示。

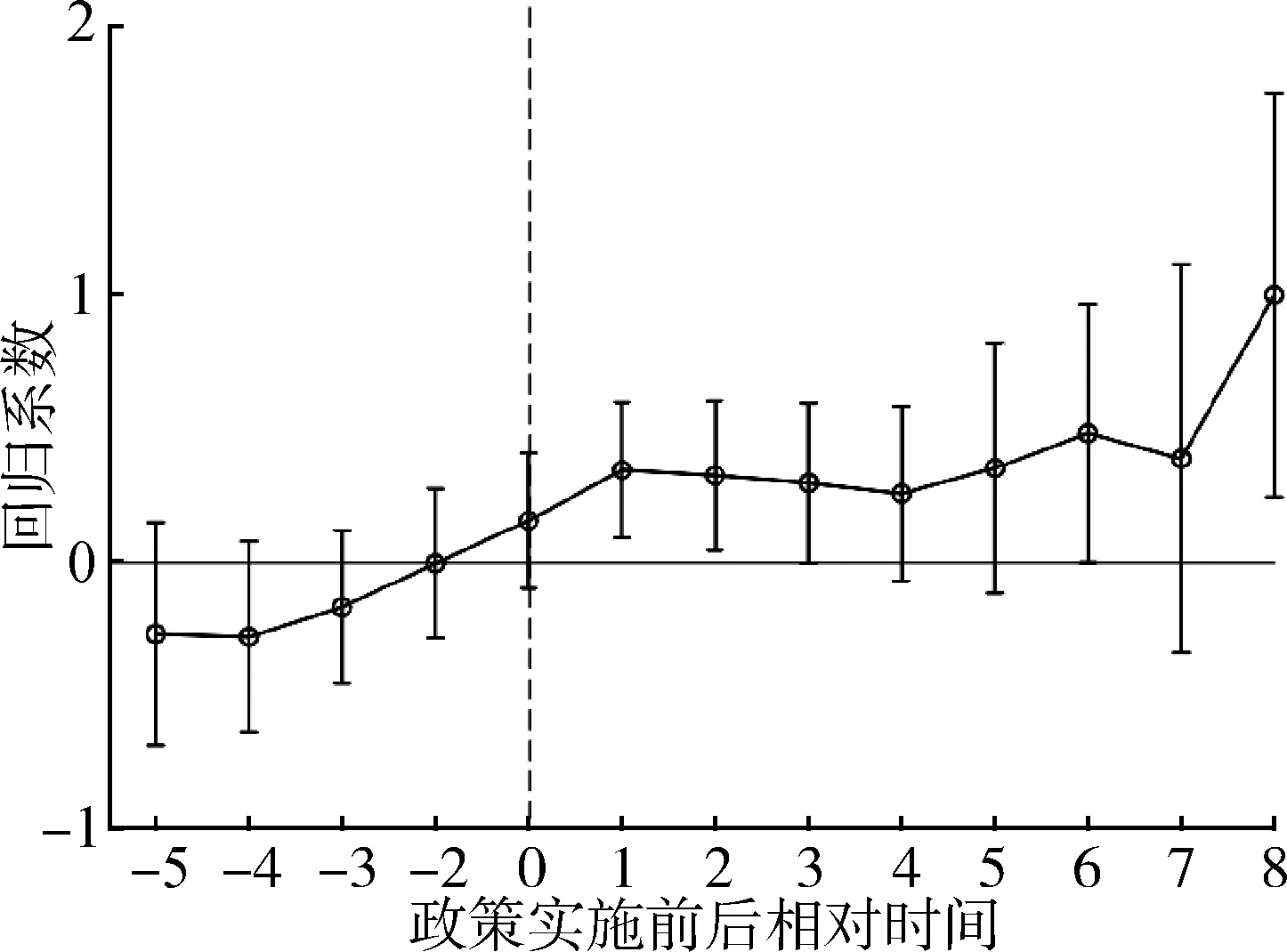
图1 平行趋势检验

基于上述原因，本文借鉴Beck等[20]的做法，对国家农业科技园区建立的平行趋势进行检验，并给出动态趋势检验图。从图1中可以看出，在政策实施之前，国家农业科技园区对农业经济增长影响的回归系数并没有通过显著性检验，说明在建立国家农业科技园区之前，建立国家农业科技园区与尚未建立国家农业科技园区的城市之间不存在显著性差异，因此满足平行趋势检验。

3.3 稳健性检验

3.3.1 替换被解释变量

考虑到中国各省份产业发展水平存在差异，运用农林牧渔总产值对农业经济增长进行衡量可能存在偏误，因此在表3的模型(3)、(4)中替换被解释变量为农林牧渔业增加值对数值(lnadd)，进一步分析国家农业科技园区对区域农业经济增长的影响。回归结果显示，无论是否考虑控制变量，国家农业科技园区均对农林牧渔增加值发挥了显著促进作用，但是回归系数较模型(1)、(2)稍有下降，具体地，国家农业科技园区的建设能够带动区域农林牧渔增加值提升3.5%。

表3 稳健性检验Tab. 3 Robustness test

3.3.2 考虑国家农业科技园区建设“强度”的影响

表2与表3的模型(1)～(4)中，一直将国家农业科技园区视为二元变量。在整理数据时发现，部分地级市拥有2个及以上的国家农业科技园区。因此在稳健性检验部分，用地级市拥有国家农业科技园区的数量(number)作为核心解释变量进行回归，观察国家农业科技园区的建设强度是否会对地区农业经济发展有不同的影响。从表3模型(5)的回归结果可以看出，国家农业科技园区的建设强度越大，越能提升当地的农业经济增长水平，并且提升水平达到了19.1%。

3.4 中介效应分析

基于技术创新的中介效应分析，如表4所示。

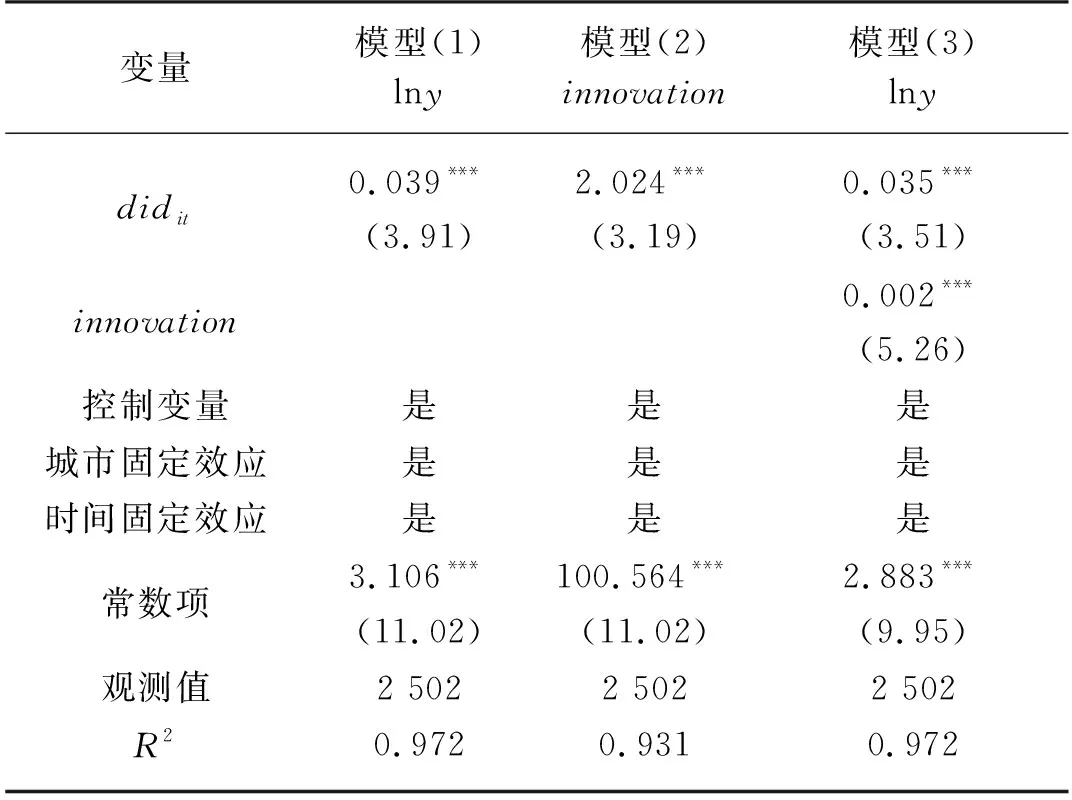
表4 基于技术创新的中介效应分析Tab. 4 Analysis of mediating effect based on technological innovation

表4中的模型(1)～(3)的回归结果均在1%的统计意义上显著，表明国家农业科技园区通过提升区域技术创新水平进而促进区域农业经济增长。技术创新在国家农业科技园区影响区域农业经济中发挥着部分中介效应。为稳健中介效应效果，本文在逐步回归系数方法的基础上又进行了Bootstrap检验，表5的Bootstrap检验结果显示偏误校正BC后的置信区间均不包含0，说明中介效应成立，国家农业科技园区对农业经济增长的总效应等于间接效应0.026加上直接效应之0.151，总效应为0.177，中介效应占比14.69%。

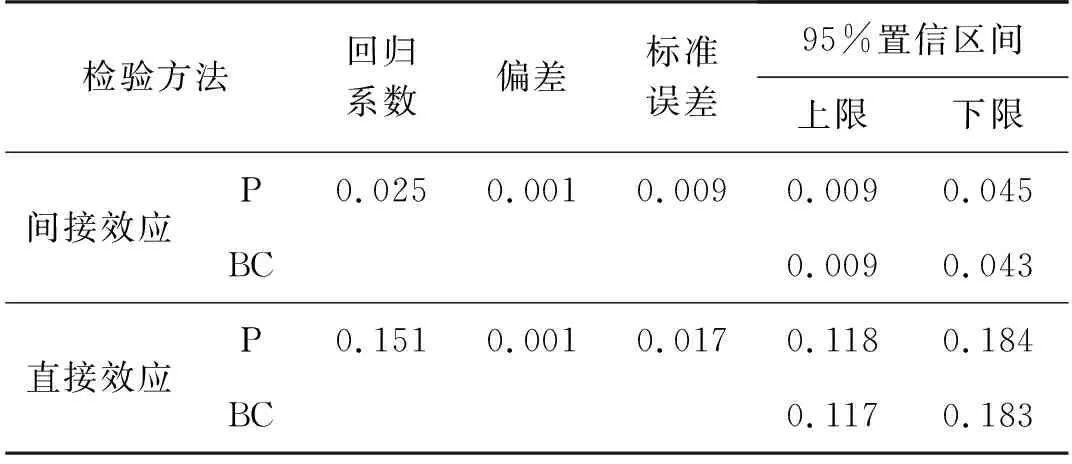
表5 Bootstrap检验结果Tab. 5 Bootstrap test results

3.5 异质性分析

3.5.1 按地理位置划分

中国长期存在区域发展不平衡的问题，相较于东部地区而言，中西部地区更加注重农业产业的发展，因此在异质性分析中，进一步探究国家农业科技园区对东部地区、中西地区农业经济增长的不同影响。按照国家统计局的划分方式对东、中西部城市进行分组，分别构建东部城市虚拟变量(eastcity)、中西部城市虚拟变量(middleweastcity)，并与didit交乘后纳入回归模型，结果如表6所示。从表6模型(1)、(2)可见，东部城市虚拟变量与didit交互后进行回归的结果并不显著，并且系数为负，可见国家农业科技园区对东部城市的农业经济增长可能存在抑制作用；中西部城市虚拟变量与didit的交互项的系数在1%的水平上显著为正，中西部地区的国家农业科技园区能够促使当地农业经济增长提升7%。一方面，我国东部地区二三产业在经济中的占比大，而第一产业占比小，因此国家农业科技园区的作用效果不强；另一方面，东部地区制造业发达，农业科技园区的技术创新成果可能更多地外溢到二三产业的发展中，从而对地区农业经济发展产生排挤效应。

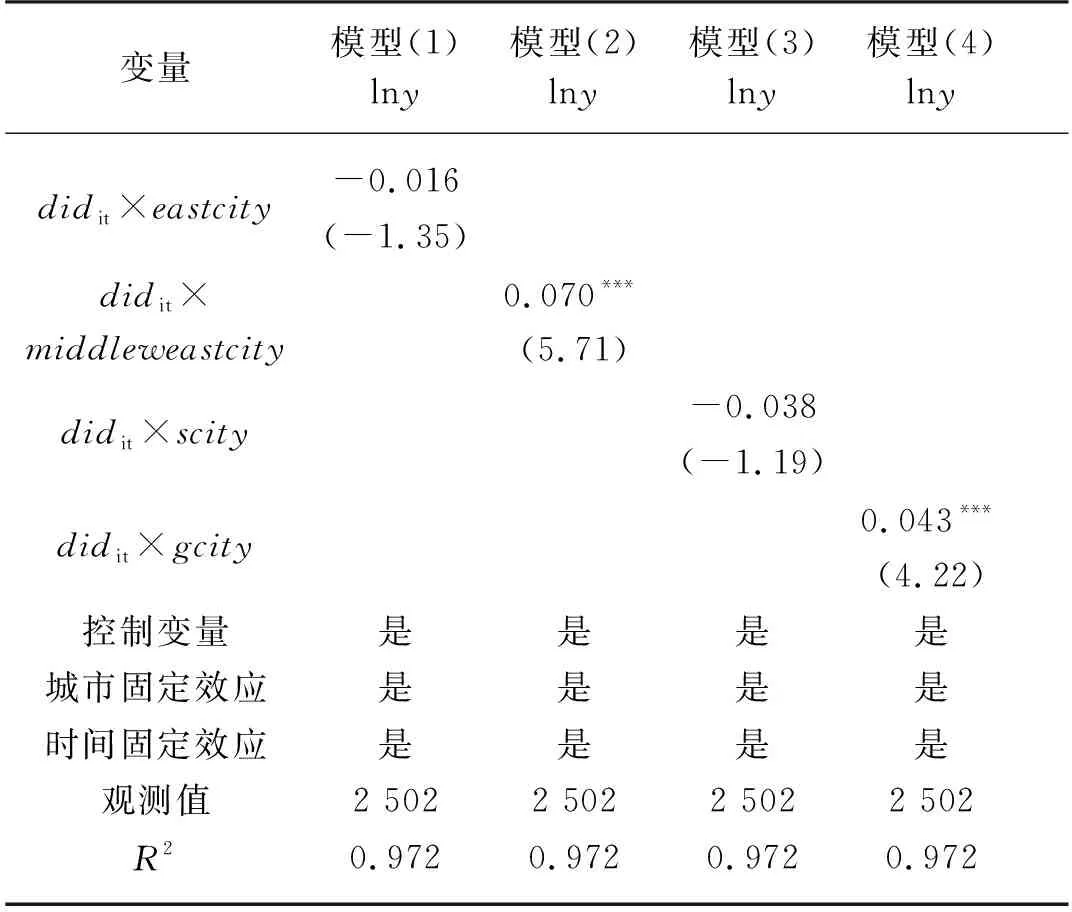
表6 异质性分析Tab. 6 Heterogeneity analysis

3.5.2 按行政层级划分

城市发展中，行政等级高的城市往往在资源集聚、技术创新更具备优势，经济发展的水平也更高。因此，不同行政层级的城市在建设国家农业科技园区的过程中可能会存在差异，本文借鉴刘哲[21]、朱金鹤[22]的研究，将254个地级市按照省会城市、一般城市分组，其中省会城市22个，一般城市232个，分别构造省会城市虚拟变量(scity)、一般城市虚拟变量(gcity)，与核心解释变量didit交互后进行回归，回归结果与按地理位置分组的结果一致。相较于省会城市，一般等级城市的国家农业科技园区能够使得区域农业经济增长水平提高4.3个百分点，这是因为相较于省会城市，一般的城市在第一产业发展上的资源投入更多，国家农业科技园区通过孵化培育农业高新技术企业，集聚农业发展要素，调整农业产业结构，提升农业综合发展效益。

4 主要结论与政策启示

4.1 主要结论

通过构建多期双重差分模型，对国家农业科技园区在区域农业经济增长中的政策效应进行检验。

1) 国家农业科技园区对区域农业经济增长发挥了显著的促进作用，建设国家农业科技园区的区域，其农业经济增长水平比尚未建设国家农业科技园区区域的农业经济经济增长水平高3.9%，结果的显著性在更换被解释变量为农林牧渔增加值和考虑到国家农业科技园区建设强度的情况下依然稳健，就控制变量的回归结果来看，农作物播种面积、农业机械总动力、粮食总产值分别能促使区域农林牧渔总产值提升28.9%、16.8%、10.4%，但农林牧渔城镇从业人员与农用化肥施用折纯量对农业经济增长不存在显著影响。

2) 中介效应的回归结果显示，技术创新在国家农业科技园区促进区域农业经济增长中发挥着部分中介效应，中介效应占比为14.69%，即国家农业科技园区能够通过提升所在区域的技术创新水平，进而影响区域农业经济增长。

3) 异质性分析中，将区域虚拟变量和城市等级虚拟变量与didit交互后进行回归，其中中西部及一般等级城市的回归结果显著为正，东部及省会城市回归结果不显著且系数为负。其中，中西部地区及一般等级城市的国家农业科技园区分别能够促使区域农业经济增长提升7%和4.3%，但是东部地区以及省会城市的国家农业科技园区对农业经济增长可能存在抑制作用。

4.2 政策启示

首先，要继续贯彻乡村振兴战略和创新驱动发展战略，坚持走科技兴农、富农的道路。我国从20世纪末开始建立国家农业科技园区至今，园区建设在质量和数量上都取得了丰硕的成果，并且农业科技园区的建设逐渐形成国家级、省级、市级的三级建设体系。园区在示范带动、产业集聚、创新孵化等方面取得了卓越成效，有力地带动了地区产业发展融合。经济高质量发展时期，要继续严格执行国家农业科技园区的申报、建设和验收工作，切实发挥好科技园区对三农的积极作用。

其次，各地要继续加强区域内的国家农业科技园区建设。从第一批试点发展至今，国家农业科技园区已经基本实现地级市的全覆盖，在新型工业、服务业快速发展的时代，应该充分利用好农业科技园区这一平台，提高园区自身的技术创新成果转化率、新品种技术的引进率，通过高技术投入和高效率产出提升农产品的经济附加值。更要因地制宜，在不断完善地区的农业产业结构的同时加快农业工业化建设，依靠国家农业科技园区形成新的产业增长极，加快三产融合发展。

最后，根据国家农业科技园区对各类人才的现实需求，建立对企业经营管理者和市场开拓人才及农业劳动者的分类培养机制。在互联网、人工智能快速发展的时期，传统的农民就业主体已经无法适应现代农业经济的发展，国家农业科技园区作为技术创新型农业组织形式，拥有丰富的科研技术人才，因此必须要发挥园区的教育培训功能，园区要定期开展对园区内外的农民的教学工作，通过实地参观、视频教学的方式，为农民普及先进的农业生产技术，培育一批职业农民投入到地区的农业发展中，提高地区农业发展中的人力资本水平。