船舶氢储电力推进系统燃料电池功率变换器设计

胡 鑫，王国玲，许顺孝，李振宇，罗成汉

(1.集美大学轮机工程学院，福建 厦门 361021；2.福建省船舶与海洋工程重点实验室，福建 厦门 361021)

0 引言

随着航运经济的发展，船舶CO2排放逐渐成为影响全球气候环境的主要因素。据统计，船舶的CO2排放量约占全球CO2总排放量的3%[1]。为解决船舶碳排放对环境的污染问题,国际对新能源船舶的需求日渐迫切。随着科学技术不断地进步，能源的持续开发，氢燃料电池以其能量转换效率高、能量密度高、零碳排放、振动噪声低、寿命长等优点，成为船舶电力推进装置的最佳选择[2]。

目前有学者对氢燃料电池功率变换器展开了研究。文献[3]采用两个交错式升压转换器作为第一部分升压电路，三级升压转换器作为第二部分升压电路，克服了传统Boost电路因为电感饱和等原因存在的升压倍数受限制问题，但未实现电气隔离；文献[4]采用四开关Buck-Boost变换器作为前级直流变换器，对氢燃料电池进行升压与稳压，该变换器无源元件少、器件应力低，效率高，适用于氢燃料电池大电流、宽电压输出的功率变换，同样的也未实现电气隔离；文献[5]采用Boost与推挽正激变换器组合的方式，实现了电气隔离，且响应速度快，但推挽正激变换器采用开环控制，易造成变换器不稳定；文献[6]采用推挽Buck型直流变换器，在氢燃料电池输出电压变化时，能够保证系统输出电压达到设定值，高效可靠，但推挽型变换器只适用于中小功率场合，且采用两个变压器，硬件电路较为复杂；文献[7]采用两个二极管和两个开关管组成全桥整流桥，能够控制变压器一次侧、二次侧开通和关断，利用变压器漏感进行能量转移，最终获得较高的能量转化效率，但增加了两个开关管，导致驱动电路较为复杂，成本较高。为了有效转换氢燃料电池的电能，本文建立了电池功率变换器的状态空间平均模型，提出电路参数以及关键控制参数设计准则，设计了变换器控制系统，最后搭建了船舶氢储电力推进系统的仿真平台，并对仿真结果进行讨论。

1 系统组成

船舶氢储电力推进系统通过氢燃料电池的能量传递以实现船舶运行的推进，在设计船舶氢储电力推进系统时，不但要考虑船舶工况，而且需结合氢燃料电池输出外特性。

深远海的海况相对较复杂，会受到天气、水流速度、风速、暗礁等诸多因素的影响，船舶工况变化呈现出随机特性。氢燃料电池输出外特性软、动态特性差，故需与储能单元并联，利用储能单元平衡负荷变化引发的功率波动，构成船舶氢储电力推进系统，如图1所示，系统参数设置如表1所示。

图1 船舶氢储电力推进系统

表1 系统参数

当船舶运行在启动、加速或者过载等暂态工况下，驱动船舶行驶所需的功率大于氢燃料电池所能提供的运行功率，由于超级电容的快速动态响应，所需的额外瞬态功率立即由超级电容补充，但超级电容能量密度低，能量存储有限，只能够持续提供大约1 min的峰值功率，当大于超级电容所能提供的额外功率时，切换锂电池，与氢燃料电池共同提供峰值功率；当船舶运行在低速、减速或者制动等暂态工况时，驱动船舶行驶所需的功率低于氢燃料电池输出功率，此时系统瞬间电流较大，由于超级电容的充电速度快于锂电池的充电速度，氢燃料电池将先向超级电容充电，避免了大电流充电对锂电池寿命的损坏。此后氢燃料电池再向锂电池充电，存储富余的能量，同时吸收存储再生制动能量。

2 氢燃料电池功率变换器功率电路设计

由于氢燃料电池输出特性软，输出电压低，峰值功率输出不足、动态响应慢，如果直接连接在船舶氢储电力推进系统的直流母线上，氢燃料电池则难以承受高比例船舶电力推进负载工况的频繁变化，从而导致船舶电力系统源-载侧功率不匹配，引起氢燃料电池输出特性改变、母线电压振荡，造成系统不稳定，因此需要增加直流变换器来提升和稳定氢燃料电池的输出电压，使其运行在最佳工作点。在此转化过程中会造成较大的电能损耗，因此，应选择合适的电路结构，提高直流变换器变换效率，以保证燃料电池电能利用率及氢燃料电池的寿命。

本文采用如图2所示的移相全桥直流变换器，通过控制四个MOSFET管S1～S4，对输入电压进行逆变，经过变压器T1升压后，在变压器副边得到交流电压，最后利用整流二极管D1～D4的单向导通特性进行整流，并通过电感电容的滤波作用减少纹波，完成DC-AC-DC的电压转换过程。

图2 直流全桥变换器电路结构

2.1 基本工作原理

移相全桥变换器驱动波形如图3所示。其中:θ表示移相角;0表示开关管关断状态；1表示开关管处于导通状态。为避免桥臂直通，开关管S1和S2的驱动信号PWM1、PWM2互补，S3和S4的驱动信号PWM3、PWM4互补，且PWM3落后PWM1一个相位角θ(0<θ<180°)。

具体工作过程如下：在[0，t1]时间段，S1、S4导通，S2、S3关断，变压器原边电压v1=Vg，与此同时，根据变压器同名端关系，变压器副边电压v2=N·Vg,次级二极管D1、D4导通，变压器原边向负载提供能量，t1时刻PWM3、PWM4反向，S4截止，由电感原理可知，变压器原边电感中的电流不能突变，S3不能立刻导通，S3的反并联二极管D7导通续流,S1与D7同时导通，此时变压器原边、副边绕组电压均为零；t2时刻，PWM1、PWM2反向，S1截止，而S2不能立刻导通，其反并联二极管D6导通续流，和D7构成电流通道，变压器原边电压为v1=-Vg，当变压器原边电感电流过零并开始反向时，S2、S3开始导通，变压器原边电压仍然为v1=-Vg，此时变压器副边电压为v2=-N·Vg,次级二极管D2、D3导通，变压器原边向负载提供能量；t3时刻,PWM3、PWM4再次反向，S3截止，而S4不能立刻导通，其反并联二极管D8导通续流，变压器原边电压再次为零。此后的过程和上面类似，这样通过改变移相角θ的大小即可调节系统输出电流，实现输出电流恒定，进而实现系统输出功率恒定，使氢燃料电池运行在最佳工作点。

2.2 功率开关器件的选型

功率开关管是移相全桥直流变换器的重要组成部分，其功能特性的优劣在很大程度上影响着整个系统的转化效率。目前常用的功率开关管主要有两种：绝缘栅极型晶体管(IGBT)和大功率场效应管(MOSFET)。IGBT在低压大电流的工作场合下，如果不能实现零电流关断，会产生较大的损耗，而MOSFET很容易实现零电压关断，并且开关速度更快，具有较好的频率特性，直流变换器的开关频率可以做得更高。

本文所设计的氢燃料电池功率变换器要求功率开关器件具有较大的电流应力，此外考虑到功率开关器件的开关速度以及系统的效率，移相全桥直流变换器的开关管采用MOSFET。

在稳态工作过程中，当S1、S4导通，S2、S3关闭或者S2、S3导通，S1、S4关闭时，桥臂上的单个开关管所承受的电压最大，最大电压即氢燃料电池的输出电压，大约45 V左右，通常保留1.5倍到2倍的裕量，因此MOSFET的耐压值取100 V较好；系统所选择的氢燃料电池模型为6 kW/45 V，此时氢燃料电池的输出电流为134 A，保留1.5倍到2倍的裕量，则单个开关管至少需满足250 A的过电流能力；此外，还应考虑导通损耗和开关损耗，因此应选择导通电阻较小，具有快速体二极管恢复特性的MOSFET。综上考虑，本文移相全桥直流变换器的开关器件选用英飞凌公司100V/290 A的IRFP4468功率MOSFET。

2.3 LCL滤波器参数设计

在直流变换器中，变换器的脉宽调制会产生大量的开关频率次谐波，为了满足系统开关频率次和倍频次谐波电流的抑制要求，必须设计合理的入网滤波器。LCL滤波器在高频段具有较好的滤波性能，可以以-60 dB/dec的速率衰减PWM引入的高频段谐波，其等效电路模型如图4所示。其中：v2为变压器副边输出电压；vo为直流母线侧电压;vx为滤波器电容C1电压；io为变换器输出电流。

由图4可得变换器输出电流与变压器副边输出电压的关系[8]，即：

(1)

(io/v2)vo=0=1/(s3L1L2C1+s(L1+L2))。

(2)

(3)

将s=jωs(ωs为系统开关频率)代入式(3)中,可得：

(4)

通常采样变换器侧电感电流时，LCL滤波器的谐振频率应小于开关频率的1/6；采样网侧电感电流时，LCL滤波器的谐振频率应大于开关频率的1/6，且小于开关频率的1/2[9]。在此系统中开关频率为10 kHz，本文采用采样网侧电感电流的控制方法，谐振频率取开关频率的1/3，变压器副边电压为v2=N·Vg，将表1中的参数代入式(4)可得L=100μH，综合考虑取L1=35μH，L2=65μH。

高频谐波输入时，滤波电容支路的阻抗随频率的增大而减小，所以滤波电容支路为高频谐波提供了低阻通路，极大减少了输出电压的高频谐波含量,取变换器的输出电压纹波ΔV=Vo×1%=4 V，输出电容在一个充放周期内吸收的能量可用式(5)表示,

C1(V0+ΔV)2/2-C1(V0-ΔV)2/2=P·(Ts/2)。

(5)

其中：Ts为系统开关周期。

由式(5)可得：C1=P/(4·fs·V0·ΔV)=6/(4×10×400×4)=94(μF)。

(6)

满足设计要求。

3 氢燃料电池功率变换器控制系统设计

由移相全桥直流变换器工作原理分析可知，在[0，t1]以及[t2，t3]时段，v2=N·Vg；在[t1，t2]以及[t3，t4]时段，v2=0。假设输入电压与v2连续且周期内变化量很小，其大小用开关周期平均值表示，则一个开关周期内平均值为：

(〈θ(t)〉Ts/180)N·〈vg(t)〉Ts。

(7)

采用线性PID控制器控制移相全桥直流变换器，由于上述系统建立在一个开关周期内，所以选取的变量都是开关周期平均值，包含了稳态值和扰动量，是非线性模型，不便于对其进行线性控制器设计。为了方便设计线性化控制器，对大信号系统模型进行线性化处理，在稳态工作点附近加入小信号扰动，即有：

(8)

其中：V2、Vg、θ分别表示稳态工作点对应的变压器副边输出电压、变压器输入电压和移相角。

将式(8)代入式(7)中，忽略直流分量以及二阶交流量可得：

(9)

经过拉式变换后，相关传递函数为：

(10)

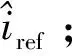
Gi(s)=(Vgkps+kiVg)/[(s4L1L2C1·180+s2(L1+L2)·180)]。

(11)

将s=jωc代入式(11)，其中ωc为系统开环截止频率，可得：

(12)

由式(12)可得幅频特性A(ω)及相位φ(ω)如下：

(13)

电流环的控制目标主要是使变换器输出电流能够快速准确地跟踪系统输出电流设定值，要求具有较强的抗扰动性能，所以要考虑系统的稳态误差。当闭环传递函数的模为1时，系统的稳态误差为0，相位滞后也为0，系统的动态响应速度无穷大[10]。此外，当系统的相角裕度为30°～60°时，系统具有良好的性能，令A(ω)=1,取ωc=0.3ωs，相位裕度取45°，由式(13)可得kp、ki。

4 仿真结果与讨论

为了验证本文所提出的移相全桥直流变换器的拓扑设计与控制设计的有效性，使用MATLAB/Simulink软件搭建包含移相全桥直流变换器、船舶电力推进单元以及储能单元的系统仿真模型，如图7所示。其中氢燃料电池所选取的模型为6 kW/45 V，船舶电力推进单元用恒功率负载代替，储能单元采用电感串联理想电压源的形式，移相全桥直流变换器系统相关参数如表1、表2所示。

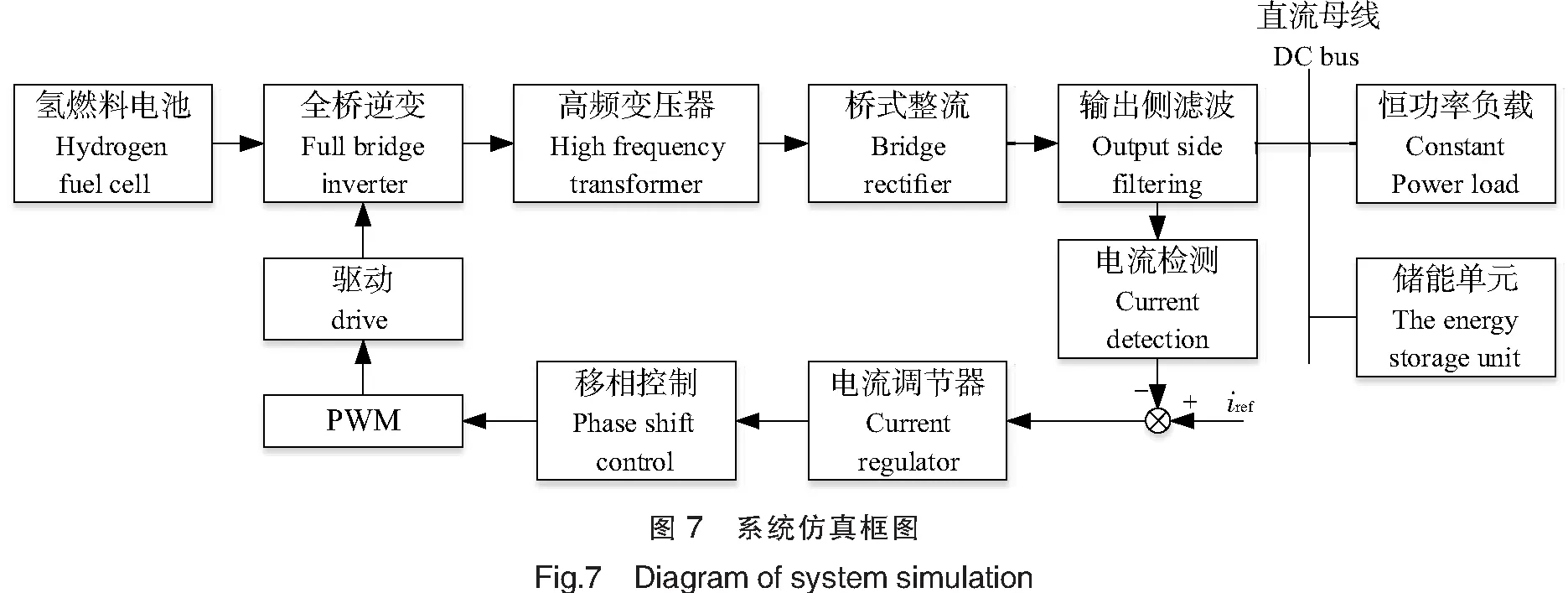
表2 系统相关参数

当开关管S1、S4导通，S2、S3关断时，此时变压器原边电压v1=Vg，副边电压为v2=N·Vg;当开关管S1、S4关断，S2、S3导通时，变压器原边电压v1=-Vg，副边电压v2=-N·Vg;其余情况变压器原边、副边电压为零。变压器原边、副边输出电压波形如图8所示。从图8中可看出，变压器原边电压约为45 V，经过变压器升压后副边输出电压约为750 V，由表1可知变压器原副边匝数比为30∶500，可见变压器工作波形正常。

设定作用于移相全桥直流变换器的初始驱动信号PWM1、PWM2、PWM3和PWM4频率均为10 kHz，占空比为50%，其中PWM1与PWM2互补导通，PWM3与PWM4互补导通，且PWM1与PWM3相位相差为180°。通过MATLAB/Simulimk软件中的示波器工具，可以观察驱动波形是否正常，测试波形如图9所示。

由图9可看出，横格每格为0.00005 s，因此一个周期为0.0001 s，对应工作频率为10 kHz。此外,开关管PWM1和PWM2互补导通，PWM3和PWM4互补导通，PWM1、PWM3或PWM2、PWM4之间的相位差为θ(0<θ<180°)，驱动波形正常，与设计一致。

对船舶氢储电力推进系统进行仿真实验，获取移相全桥直流变换器在负载突变时的输出波形，如图10所示。

系统开始工作时，变换器能够快速稳定在输出电流设定值，稳定输出功率6 kW，且输出电流纹波、输出电压纹波以及超调量都较小，控制效果良好。当t=0.373 s时，投入6 kW的恒功率负载；当t=0.69 s时，切除6 kW的恒功率负载。

从图10中可看出，变换器能在0.5 ms的时间内快速稳定在输出电流设定值，基本稳定输出功率为6 kW，最大电压变化量为0.3 V，最大电流变化量为±0.1 A，满足设计要求。

仿真结果表明，移相全桥直流变换器在负载发生突变时输出电流能够在短时间内达到所设定的值，变换器功率恒定输出为6 kW,保证了氢燃料电池工作在最佳工作点。

5 结论

本文从氢燃料电池的输出特性出发，采用移相全桥直流变换器来提升和稳定氢燃料电池的输出电压，使其工作在最佳工作点，解决了当船舶工况频繁变化时船舶电力系统源-载侧功率不匹配问题。仿真结果表明，移相全桥直流变换器作为船舶氢储电力推进系统中氢燃料电池功率变换器的电路拓扑方案具有良好的工作特性，当负载突变时能够快速准确地跟踪系统所设定的输出电流基准，恒定输出功率6 kW,改善了氢燃料电池的输出特性，实现了电气隔离，提升了系统的安全性能。