电驱动引发液滴弹跳过程中的能量转换*
刘小娟 李占琪 金志刚 黄智 魏加争 赵存陆 王战涛†
1) (中山职业技术学院机电工程学院,中山 528400)
2) (西安交通大学能源与动力学院,西安 710049)
1 引言
固液分离在许多工业过程(如凝结散热[1,2]、机翼除冰[3]和燃料电池[4])中扮演着重要的作用.在凝结散热过程中需要将冷凝液滴迅速从表面清除以改善传热效果,重力去除液滴是最常见的机制,但是这种方法限于重力作用方向,并且仅对一定尺寸的液滴有明显效果.为了从固体表面脱离,液滴往往需要获得额外的能量.这种外加的能量可以通过两个或多个液滴聚合获得[5-7],也可以通过外加激励输入能量来实现[4,8,9].冷凝水可以在超疏水表面上通过液滴聚合自动离开表面,液滴合并变形会制造出多余的表面能,这部分表面能可以帮助液滴克服表面吸附和摩擦力,进而从所接触的表面跳起,促进凝结散热.该过程被称为逐滴冷凝(dropwise condensation),其散热效率比基于薄膜冷凝(film-wise condensation)的效率高一个数量级.通过液滴自发合并达到固液分离是一个被动的过程,不便于主动控制.另外,粘附在固体表面的液滴也可以通过对底面瞬间加热形成Leiden Frost 液滴从固体表面脱离[8],但是这种做法能耗太大,而且容易造成固体表面或液滴成分的破坏,因此不适合推广.
近年来,相关研究表明电润湿可用来提高冷凝散热的效率[10],用于引发液滴弹跳[11-13]和驱动液滴三维传输[14].电润湿是一种利用电场激励改变液体在固体表面润湿性的一种方法,最早由德国科学家Lippmann 提出[15],后来Vallet 等[16]在Lippmann 实验的基础上引入了介电润湿概念,通过在电极上涂覆介电(绝缘)薄层,极大地减小了液滴中的电流,并显著增大接触角的调控范围,从而使该操作成为非常流行的一种主动式微流控技术.目前介电润湿(下文统称为电润湿)技术已经在液滴透镜、光电显示和芯片实验室中取得了愈加广泛的应用[17,18].
近期同济大学Zhang 等[19]以及南洋理工大学Vo 和Tran[20]对电场驱动的液滴弹跳的条件提出了理论预测,但他们仅考虑了直流电场激励下液滴变形始终为球缺的条件,而没有考虑交流激励下的液滴振荡变形的情形.中国科学院钱学森空间技术研究所Wang 等[21]利用逆电润湿效应驱动油相液滴在水相环境中弹跳,并对激励液滴弹跳的阈值电压提出了理论预测,同样他们的模型中没有考虑液滴振荡变形的黏性耗散.我们之前已经报道了电润湿激励引发的液滴弹跳并分析了激励信号和弹跳高度的关系[13],指出在引发液滴弹跳中交流脉冲比直流信号更有效.在由电润湿引起的液滴弹跳过程中,会发生电能、表面能、动能和内能的相互转换,这一复杂的能量转换过程至今还没有被系统报道过.本文将对该过程中涉及的能量传输进行具体分析,为相关应用提供理论参考.
2 研究方法
2.1 实验方法
电润湿驱动液滴弹跳是通过引发液滴变形并获得额外的界面能而发生的.在电压激励下,输入的电能以等效电容方式改变固-液界面能,引起宏观接触角减小、液滴变形和整体表面积增大.在脉冲移除以后,固液界面张力恢复,三相接触线回缩,驱动液滴接触角和整体形状的恢复.本研究设计加工了用于液滴弹跳的数字微流控芯片,芯片采用间隔对称分布的共面电极,利用直流和交流电压激励超疏水芯片上的水滴,在空气环境中实现液滴的弹跳.另外,利用高速摄像机捕捉超疏水表面的液滴在交流脉冲激励下的从固体表面的脱离、振荡和弹跳的现象,进而分析液滴的运动轨迹和内部流动.通过对液滴形状进行勒让德分解,量化在液滴变形、弹跳、飞行和撞击过程中的各种能量形式.
本实验中使用的数字微流控芯片采用多层分布.如图1 所示,芯片的底层是玻璃,上面是磁控溅射形成的ITO(氧化铟锡)电极,ITO 上面是经旋涂的厚度约为5 µm 的聚四氟乙烯.聚四氟乙烯经氧气等离子处理形成纳米至微米级粗糙度,结合其自身的疏水性获得超疏水材料.芯片采用对称分布的共面(co-planar)电极.电极包括驱动电极和参照(接地)电极,驱动电极和参照电极间隔排列,间隔20 µm .同类电极串联在一起,连接到电源的同一极.激励装置包括信号发生器和放大器.利用信号发生器(33220 A,Agilent) 产生直流和交流激励,其中交流激励为长度可调的脉冲(10 kHz 正弦波).电压信号经放大器 (Trek PZD700A)放大以后激励体积约为4 µL 的微小液滴,之后利用高速摄像机(Fastcam Ultima)结合背景光源以2000—5000 帧/s 的速度捕捉液滴运动.PC 用于存储和处理高速摄像机记录的图像和视频.试验在万级洁净室中进行,液滴是去离子水(MilliQ water),通过流量精确控制的注射装置将预定体积的液滴放置到芯片的中心,确保液滴的底部同时和参照电极和驱动电极重叠.
2.2 液滴在电场激励下变形和振荡的理论分析
如果附加的表面能量足够克服表面的吸附功和摩擦力,液滴就会脱离表面发生弹跳(见图2).因为液滴的半径约1 mm,而实验中使用的超疏水表面接触角很大(θ0≥155°)且接触角滞后非常小(Δθ≤8°),在阈值估算中忽略重心位置变化的影响,即液滴弹跳仅需克服固体表面和液滴之间的吸附功[19].在共面电极配置下,考虑到超疏水表面的Cassie 润湿接触角方程和吸附功的表示方法[22-24],得到以下表达式:
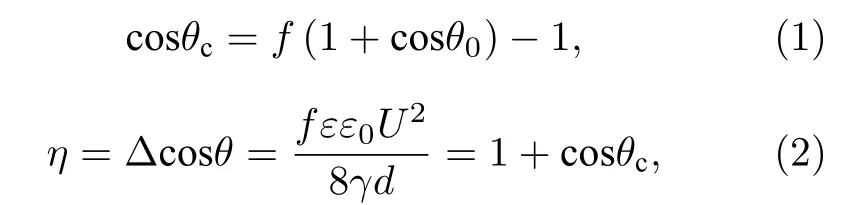
其中θ0为芯片最表层C4F8 的原始接触角,经测量为103°,θ为液滴的电润湿接触角,η为表征电润湿效应的电润湿数,θc为液滴在超疏水表面处于Cassie 润湿状态的初始接触角,f为固-液接触面积分数,ε和ε0分别为绝缘层的介电常数和真空的介电常数[21].γ是液滴的表面张力,约为 72 mN/m ;d为绝缘层的厚度,设计为5 µm .
在直流电压激励下,液滴的变形遵循等体积球缺的原则.在移除电压时,电容放电速度远大于液滴界面的变形速度,固液界面张力瞬间恢复,但液滴整体仍然保持着原来的形状[25].在移除电压时液滴界面的能量是球缺的上盖表面能和基底的界面能之和.根据球缺的面积计算公式,液滴的界面为
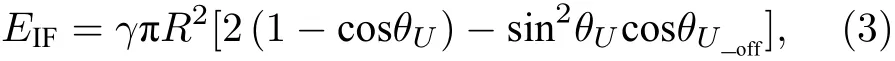
其中θU代表液滴在电压激励下的接触角,θU_off为移除电压以后的接触角.移除电压时固液界面张力瞬间恢复,则 c osθU_off=cosθc≈-1,以上方程可以简化为
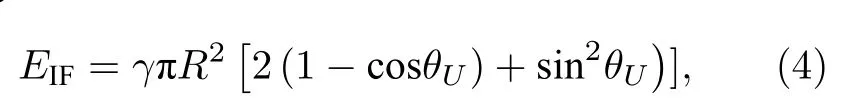
即EIF成为θU的函数.
为方便计算,假设在直流激励下液滴从表面脱离后呈理想球体(图2),其体积为V=R0为球体半径.与理想球体相比,液滴因在电润湿激励下变为球缺所引起的界面能的增大为


图2 250 V 直流电压激励下液滴的变形和弹跳,从左至右分别为液滴在激励前,激励中和激励移除以后的状态Fig.2.The deformation and bouncing of the droplet under the excitation of 250 V DC voltage,from left to right are the states of the droplet before excitation,during excitation and after excitation removal.
假设表面能可以全部转化为液滴的重力势能,则液滴大弹跳高度应为

交流电压激励下的液滴受到随时间变化的电场力,继而在表面张力的作用下引发液滴产生动态形变[26-29](见图3).在激励电压超过一个特定阈值时,液滴会发生弹跳现象(见补充材料录像).液滴在空中飞行一段时间以后,会在重力作用下重新撞击固体表面,进而发生在固体表面的反复弹跳直至最后静止.因为表面张力的作用,液滴在整个运动过程中会以一定的频率振荡,这种振动在黏性阻滞作用下会随着时间衰减,并且会因为和固体表面的撞击而变化.

图3 电润湿激励下的液滴变形和弹跳,从左向右每帧间隔为1 msFig.3.Droplet deformation and jumping under electrowetting excitation,the interval between two adjacent images is 1 ms.
液滴在交流激励下的变形相对复杂,难以用一个准确的分析模型描述.为了研究液滴的质心运动和振荡变形,在Matlab 中利用边缘检测的方法从图1 所示的侧视图中将液滴轮廓(边线)提取为时间函数,并使用勒让德多项式将液滴的轮廓相对于其几何中心的坐标分解为球谐函数.变形后的液滴轮廓被利用勒让德多项式进行正交分解,得出各个模式对液滴变形的贡献系数:
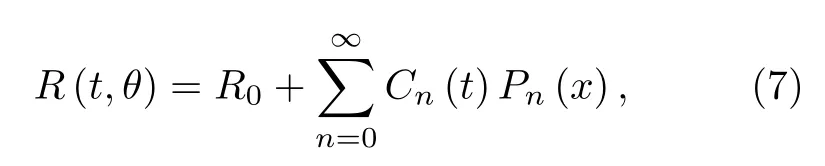
其中Pn(x) 是n阶勒让德多项式,Cn为勒让德多项式的系数,x=cosθ.令液滴的质心的纵坐标为y0,C1表示液滴质心的几何位置相对于初始质心位置的偏移,二阶以上的系数Cn给出了其余对应变形模式的贡献.系数Cn可以通过下面的公式进行计算:

在提取液滴的轮廓线时,对液滴进行轴对称处理,利用Matlab 中编写的边缘检测程序得到液滴一半的轮廓点集合 (xi,yi),并相对于对称轴x=x0进行镜像;在-1 ≤cosθ≤1的区间取迭代步长 Δcosθ=10-3,使用初始值的y0和(xi,yi)得到对应极坐标下的轮廓点集合R(t,θ) .液滴形状的变化可以完全被系数cn(t) 表征,而液滴质心轨迹可以表示为
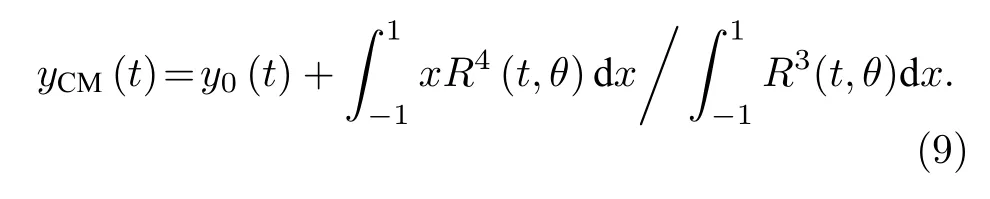
液滴质心的飞行轨迹可以拟合为一个抛物线,通过将质心的纵向位置yCM(t) 在[t-2Δt],[t-Δt,t,t+Δt,t+2Δt]的区间进行二阶多项式的拟合,取 Δt=0.25 ms,得出的一阶导数和二阶导数即为质心的速度和加速度.质心的势能和动能分别为yCM和的函数:
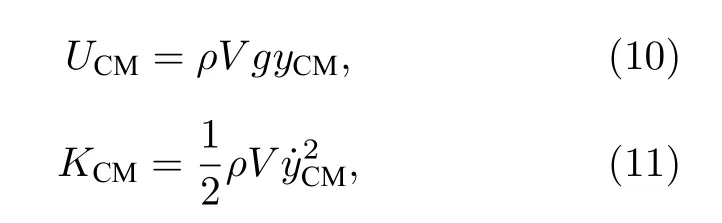
其中ρ和V分别为液滴的密度和体积,分别是1 kg/dm3和4.2 µL.另外,液滴轮廓相对中心随时间的变化速率,即内部势流的速度和加速度是勒让德多项式系数的一阶导数和和二阶导数,也是通过类似上述的方法得到的.
液滴的振动势能是变形状态下的液滴的表面能,其在球面坐标下的计算法方法为

其中R是液滴轮廓上一点对应的半径,随着该点相对于质心位置的角度而变化.利用液滴轮廓的勒让德多项式分解,液滴的表面势能可以表示为系数Cn的函数:

其中有效弹簧常数为keff,n=4πγ(n-1)(n+2)/(2n-1),在n≥2 时该系数收敛为keff,n=2nπγ.
液滴振动变形引起的动能(区别于质心动能)是由液滴内部的势流决定的.在忽略液滴黏性的前提下液滴内部势流简化为v=∇ϕ.由于液滴不可压缩,势流应满足拉普拉斯方程∇2ϕ=0 .利用∇(ϕ∇ϕ)=∇ϕ·∇ϕ+ϕ∇2ϕ=∇ϕ·∇ϕ和散度定理,液滴的体积分可以转化为对界面的面积分:
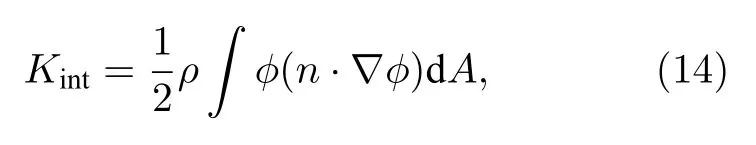
利用勒让德分解对上式进行变形得到:

虽然上述分析势流假设流体是无黏性的,可以在流体低黏度的限制下计算流场中的耗散.以应变张量的速率D表示内部耗散率,则流场中的内部耗散W可以表示为
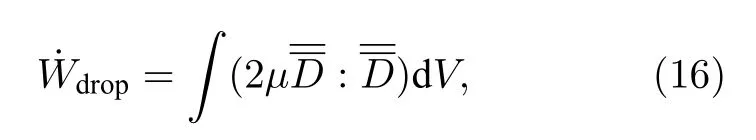
其中µ为液滴的黏度,利用勒让德分解,可以推导出[29]:
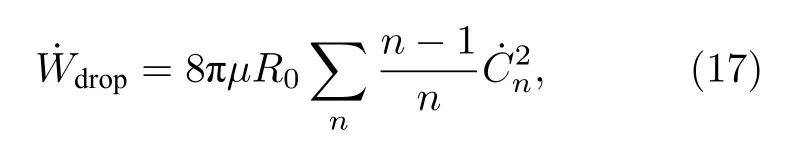
另外,液滴自由振荡的瑞利频率为
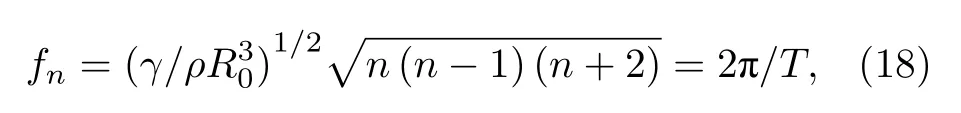
其中,T为液滴对应模式n的振荡周期.
3 结果和讨论
图4 所示为400 V 直流和交流激励下液滴的弹跳高度.其中,在直流激励下,一个电压幅值对应一个弹跳高度,与信号的作用时间无关;在交流激励下,液滴的弹跳高度不仅与电压幅值有关,而且随着脉冲长度而变化.液滴弹跳高度随脉冲长度的变化主要是由交流激励下液滴的振荡变形引起的,这种液滴在交流激励下的周期性衰减变形可以被用于优化激励信号,以提高表面能向动能的转化效率[13].
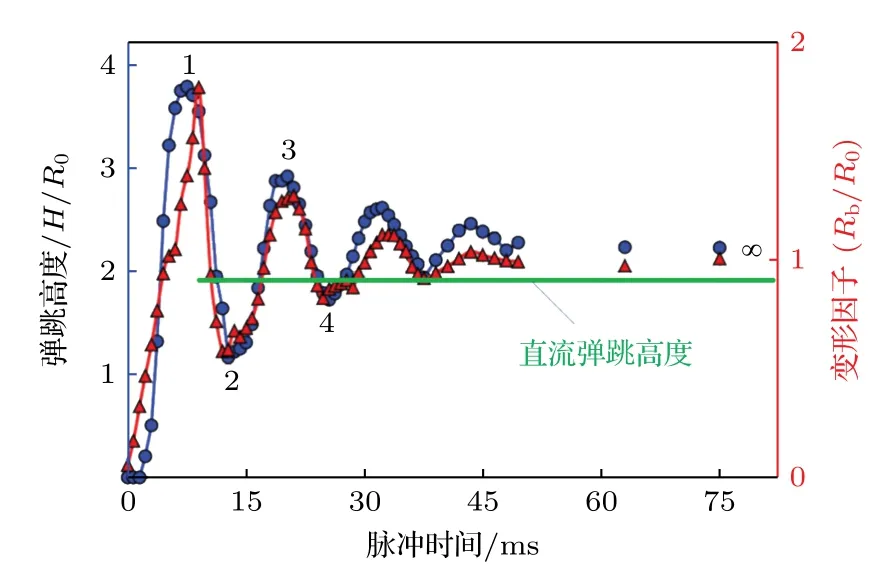
图4 无量纲化的液滴弹跳高度(蓝色)和形变因子(红色)随400 V 交流正弦波(10 kHz)脉冲长度的变化,绿色直线代表直流激励下的弹跳高度Fig.4.The dimensionless droplet jumping height (blue) and deformation factor (red) as a function of 400 V sine wave(10 kHz) pulse duration.The green straight line represents the bounce height under DC actuation.
图5 代表液滴在直流电润湿作用下的界面能(实心方块)以及移除电压以后的界面能(空心圆圈),X轴代表液滴球缺的底面半径,即液滴的变形因子,利用等效半径R0进行了无量纲处理.两条曲线代表了电场的施加和移除所引起的固-液界张力的变化,利用γπR2进行了无量纲处理.在固-液界面张力一定的情况下,同一条曲线代表液滴总界面能随着底面半径Rb即液滴形状的变化.同一个Rb对应的两条曲线的纵坐标之差代表在移除电压的瞬间因为固液界面张力的变化(恢复)而引起的总界面能的增加.从图5 可以看出,在直流电压激励下,液滴接触角由164°降为100°,液滴从一个近似球体变为一个球缺.在电压被移除的瞬间,液滴虽然保持球缺的形状,但其固液界面张力已经恢复,总界面能已经大幅增大(ΔE).

图5 液滴在电润湿作用下界面能(空心圆圈)以及移除电压以后的界面能(实心方块),Rb 代表液滴球缺的底面半径.两条曲线上相同的Rb 对应的两点具有同样的形状,同一条曲线上不同的点具有相同的固-液界面张力 γSL .注意液滴的界面能和底面半径均经过了无量纲处理Fig.5.The interfacial energies of the droplet under electrowetting (open circles) and after removing the voltage(solid squares),the X-axis represents the base radius of the droplet.The same abscissa (Rb) represents the same droplet shape,and different points on the same curve have the same solid-liquid interfacial tension.Note that both the interfacial energy and base radius of the droplet are dimensionless.
因为本实验所用的液滴等效球体半径约为R0=1 mm,远小于毛细长度(2.7 mm),因而重力对形状的影响可以忽略[23].液滴的表面张力约为72 mN/m,超疏水表面的原始接触角经测量为103°,液滴在超疏水表面处于Cassie 润湿状态的初始接触角取值为155°.绝缘层的厚度d经测量约为5.1 µm.通过方程(1)可以得到超疏水表面固-液原始接触面积分数f约为0.09.通过(2)式得到激励液滴弹跳的阈值电压为237 V,这和实验得到的可以引发液滴弹跳的阈值电压(225 V)十分接近,其微小误差很可能是因为方法中没有考虑触角滞后的影响.
液滴在脱离表面以后会在重力和表面张力的作用下发生反复弹跳,并伴随着振荡变形,这在交流激励下尤为明显.液滴的弹跳高度和表面积随时间的变化如图6 所示,在300 V 直流电压激励下液滴的起跳高度约为2 个等效半径(R0≈1 mm).液滴的形变所引起的表面积的变化约为液滴总表面积的23%,也即输入电能所引起的表面能的增大幅度.根据液滴的起跳高度,可得出液滴动能与表面能的比值ρv2R0/γ,即韦伯数(Weber number),约为0.27,即表面能高出动能数倍.跳起后的液滴在超疏水表面上弹跳高度因为能量耗散的原因逐次递减,液滴弹跳的恢复系数(restitution coefficient)约为0.85.液滴的表面积也随着液滴的弹跳逐次递减,并伴随着高频阻尼振荡.其振荡周期约为8.3 ms,与利用(14)式计算所得基本模式(即模式2)的周期相吻合.

图6 液滴质心高度和表面积在液滴弹跳过程中随时间的变化Fig.6.Variation of droplet centroid height and surface area with time during droplet bouncing.
交流激励引发液滴动态变形,相对直流激励产生更多的表面能,因此同样的脉冲幅值下跳得更高.图7 显示了交流电场驱动的液滴弹跳过程中的质心能量转化.激励初期由于液滴在电润湿作用下获得初始速度,接触线铺展导致液滴质心下移,其动能小幅增大,同时重力势能减小.液滴底面半径在脉冲移除的瞬间达到最大值,此刻液滴的速度和动能同时减为0,其重力势能因为质心达到最低点处于最低值,因此液滴的质心能量处于最小值.在移除激励后液滴接触线迅速回缩,此时液滴质心向上移动,动能和重力势能同步增加.液滴动能在其脱离固体表面的瞬间达到最大,之后因为重力作用液滴的质心速度减小,其动能和势能随着液滴的谐振做小幅振荡.
在液滴的飞行和振荡过程中,其质心动能和势能相互转换,质心总能量在 9×10-8J 左右小幅振荡,振荡频率和液滴的固有频率一致.液滴的质心动能在液滴达到最高点时候再次减为零,此时重力势能达到最大值.之后,液滴下行,液滴重力势能向质心动能转化.液滴动能在液滴重新接触固体表面的时候达到最大值,然后在固体表面作用下液滴被纵向压缩,质心动能和重力势能同时减小,直至达到最小值(见图7).然后液滴在表面张力和固体反作用下向上弹跳,动能在和势能同步增加,动能在液滴脱离固体表面的瞬间达到最大,然后向势能转换,液滴在多次的弹跳中重复这个循环.

图7 液滴在弹跳过程中质心能量随时间的变化,其中液滴质心的动能(红色)和势能(蓝色)是分别结合实验数据利用方程(10)和(11)计算得出,质心的质心总能量(黑色)是以上两部分的总和Fig.7.Variation of the droplet centroid energy with time during the bouncing process.The kinetic energy (red) and potential energy (blue) of the droplet are calculated using Eqs.(10) and (11) based on experimental data,respectively,and the total energy (black) of the centroid is the sum.
液滴在和固体表面接触时变形幅度最大,其表面积变化也最大,而在表面张力一定的情况下,表面积大小与表面势能成正比.图8 所示是液滴振动过程中内部势流所携带的动能和液滴振荡变形所产生的表面势能随时间的变化.在固体表面的反作用下液滴发生横向变形,振动势能即表面势能先增大然后减小,其最大值约为 1.55×10-7J .内部势流流场中的动能具有两个最大值,一个在液滴最大变形之前约为 0.5×10-7J,一个在液滴最大变形之后约为0.4×10-7J,在液滴质心达到最低值,即流动反向时几乎为零.在过渡到随后的飞行阶段(脱离固体表面)时,液滴继续振荡,振幅和振动能量锐减,但动能和势能仍然在不断转换(见图8).液滴振动(表面)势能和振动动能(内部势流)在脱离固体表面之后保持一定程度的耦合关联,振动总能量在液滴飞行阶段相对稳定,并小幅衰减,并在接触表面之前的瞬间达到最小值.液滴会在弹跳周期里面重复上述变化,直至最后静止.

图8 液滴的振动能量转化图谱,其中振动动能(粉色)和振动势能(蓝绿)分别是结合实验数据利用方程(13)和(15)计算得出,液滴的振动总能量(紫色)是以上两部分之和Fig.8.Vibrational energy conversion spectrum of droplet.The vibrational kinetic energy (pink) and vibrational potential energy (blue-green) are calculated using Eqs.(13) and(15) based on experimental data,respectively.The total vibrational energy (purple) of the droplet is the sum.
图9 显示了液滴在多次弹跳过程中质心能量、振动能量以及两者的总和(总能量),内部的黏性耗散以及液滴总能量和内部耗散之和.超疏水表面的液滴在交流脉冲的激励下会发生动态变形和弹跳,在此过程中液滴的能量通过多种途径发生耗散和转化.液滴的附加能量来自交流脉冲激励输入到固液界面双电层中的电能.脉冲激励首先引发液滴变形(使液滴偏离球体)产生附加的表面能(即振动势能).表面能的一部分在随后的液滴接触线回缩中转化为质心的动能和重力势能,一部分通过内部黏性阻滞所耗散.

图9 液滴在多个弹跳周期中的总体能量演化,其中内部耗散是结合实验数据利用方程(17)计算得出Fig.9.Overall energy evolution of a droplet over multiple bounce cycles.The internal dissipation is calculated using Eq.(17) in combination with experimental data.
液滴的质心动能和重力势能在飞行阶段存在耦合关联,其总值只有小幅振荡.液滴在飞行阶段保持阻尼振荡,其内部势流所携带的动能和表面势能在飞行阶段也存在一定程度的耦合关联.在飞行阶段,质心能量和振动能量之间不存在耦合,这是符合理论预期的.该阶段液滴内部能量的周期性下降完全归因于液滴中的黏性耗散,因为两条线的方向正好相反.
液滴的振动能量(内能)每经历一个振荡周期会有所衰减,这是由内部黏性耗散所引起的,内部耗散可以通过对(17)式进行积分而得出,从图9可以看出,黏性耗散随着液滴在固体表面的弹跳递增,最后占总能量的25%左右.然而总能量在所示5 次弹跳过程中的损失约为70%,这表明另外约45%的能量是通过其他渠道耗散的.有关文献表明该部分是通过液滴在撞击超疏水固体表面时所形成的气膜耗散的[30,31].对该部分能量的定量分析需要对气膜形态的动态演变进行表征,这超出了本文的研究范围,将在后续研究中进一步探讨.
通过(14)式估算出液滴的固有振荡频率为126 Hz,即液滴的铺展周期约为8 ms.因此可设计脉冲长度使之与铺展周期吻合,这样可将电润湿激励和液滴自身的振荡同步起来,用以提高弹跳的高度和能量转化的效率.通过比较图7 和图8 可以得出,在最佳脉冲长度下,界面能向重力势能的最大峰值转化效率可达30%以上.
4 结论
电润湿激励是实现液滴从固体表面脱离的一种有效可控的方式,在凝结散热和液体空间传输中具有巨大的应用潜力.本文结合实验数据和理论分析,系统研究了该过程中的能量转换过程,得出以下结论.
液滴在直流激励下的变形遵循体积不变的球缺模型,液滴的最终弹跳高度只与固液界面有效张力变化有关,即取决于激励电压的幅值.交流激励下液滴发生动态变形,不再遵守球缺模型,弹跳高度和脉冲长度有关.
液滴弹跳过程中会发生表面能、动能、重力势能和内能的相互转化.液滴质心的动能和势能在液滴脱离表面飞行期间存在明显的耦合转换关系,总量有小幅振荡.其中表面能向重力势能的峰值转化效率可达30%以上,这可通过同步脉冲长度和液滴振荡周期来取得.液滴的振动能量包括振动动能和振动势能(表面能).振动能量在液滴质心最低时达到最大,在液滴跳起以后迅速衰减,并在液滴的弹跳过程中呈现周期性衰减.振动动能和势能在飞行阶段也存在一定的耦合关系.液滴黏性引起的内部耗散随着液滴振荡变形的幅度增加,并一直存在于液滴弹跳的周期性运动中.本研究得出的结论对利用电润湿激励实现液滴三维传输具有有益的参考价值.荷兰特温特大学复杂流体物理组的Frieder Mugele 教授在理论方面给作者提出了有益的建议,在此诚挚感谢.

