基于大掠射角海底反射特性的深海地声参数反演*
黎章龙 胡长青 赵梅 秦继兴 李整林 杨雪峰
1) (中国科学院声学研究所东海研究站,上海 201815)
2) (中国科学院大学,北京 100049)
3) (中国科学院声学研究所,声场声信息国家重点实验室,北京 100190)
1 引言
海底声学参数的获取对于海洋声学研究,特别是对水下声传播及海底声学勘探等研究领域有着十分重要的意义.声学方法反演地声参数拥有测量范围大、高效且低成本等优点,反演结果的精度往往可以满足工程需求.因此,声学反演方法是获取海底声学参数的重要手段.
目前国内外对海底声学参数的声学反演做了大量的研究.海底反射系数或海底反射损失[1-8]是海底对声场作用的直接体现,是重要的地声参数反演物理量,利用其幅值、干涉周期、角度域或角度-频率域等特征可进行反演方法的设计.船舶噪声、环境噪声[9-13]等机会声源因获取方便也被利用进行地声参数反演,将机会声源的时频特性、垂直或水平相干性等特征结合贝叶斯估计、时间反转镜等方法,实现地声参数的被动反演.联合反演[14-18]主要利用了地声参数与不同匹配物理量之间的敏感性差异,如脉冲到达波形、简正波频散特性、第一影区上的传播损失、低声速沉积层下的海底反射损失干涉结构等对海底声速敏感,而远距离上的传播损失对海底吸收系数敏感等.联合反演使得地声参数可逐步、独立地反演,参数间耦合降低,这一点在分步反演策略中值得借鉴.
前人对地声反演的研究大部分集中在浅海,因为海底在浅海声传播中作为重要的边界,与声波作用次数较多,实验所获得的信号拥有着大量的地声参数信息,有利于声学反演工作的开展.相比于浅海,深海由于波导特性的缘故,往往需要在大掠射角情况下进行实验测量,此时声波与海底充分作用,海底反射信号携带着地声参数信息.本文认为大掠射角为声线出射掠射角大于海底临界掠射角.
因为深海波导中经海底反射的信号具有地声参数信息,本文选择海底反射系数进行深海地声反演,并主要针对以下几个方面展开研究.
一是理论分析分层吸收介质下吸收系数对海底反射系数的影响.分层海底引入吸收系数后,吸收系数与反射系数各子项都有关.在前人利用海底反射系数进行地声反演研究中,鲜有关注吸收系数影响分层海底反射系数物理机理的研究.
二是提出1/4 振荡周期频率下,沉积层吸收系数与基底声速的解耦合.在前人利用海底反射系数幅值进行地声反演时,沉积层吸收系数往往由于与其余地声参数耦合而无法准确反演[4,19,20].本文从海底反射系数角度,发现了在1/4 振荡周期频率下,相比于其他频点,沉积层吸收系数与基底声速的耦合程度较低.通过在1/4 振荡周期频率下合理假设沉积层吸收系数,实现基底声速和沉积层吸收系数分别一维反演,实现一定程度上的解耦合.
三是提出基于大掠射角海底反射特性的分步反演深海地声参数方法.在前人利用海底反射系数进行地声参数反演的研究中,大部分都直接构建以海底反射系数幅值为匹配参量的代价函数,并利用遗传算法等全局寻优算法进行非线性反演,可以给出各地声参数的全局最优解.但高维反演的效率较低,特别是将海底建模成两层时,不考虑剪切效应,反演参数维度就高达七维,且需要通过后验概率密度分析进行寻优结果的判断.本文利用海底反射系数在大掠射角下,不同频率下具有的特征构建分步反演方法,实现深海地声参数的线性反演.
2 分层吸收介质的海底反射系数
对于两层海底模型,可看作是三种介质间的反射问题,如图1 所示.

图1 两层海底模型的反射Fig.1.Reflection of the two-layer seabed model.
海水、沉积层与基底声速分别为cw和cs,cb,密度分别为ρw和ρs,ρb,沉积层厚度为d,沉积层和基底吸收系数分别为αs和αb,三种介质中入射角和透射解分别为θw,θs和θb.
布列霍夫斯基赫[21]给出了三层吸收介质下的反射系数表达式:

其中,Vws和Vsb分别表示海水-沉积层界面、沉积层-基底界面的反射系数.在布氏反射系数的基础上,令

Zj=γj+iµj,j=w(water),s(sediment),b(bottom),(3)
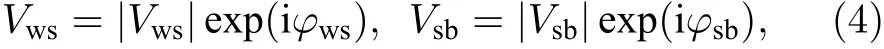
其中
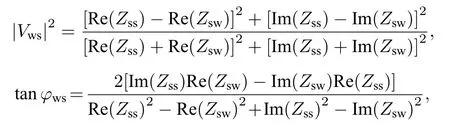
式中的Zsw和Zss分别为海水法向声阻抗率和沉积层法向声阻抗率.将下标做相应的替换,即得到|Vsb|2和 t anφsb,代入布氏反射系数表达式得:
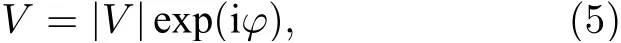
其中|V|为反射系数幅值,φ为反射系数相位:
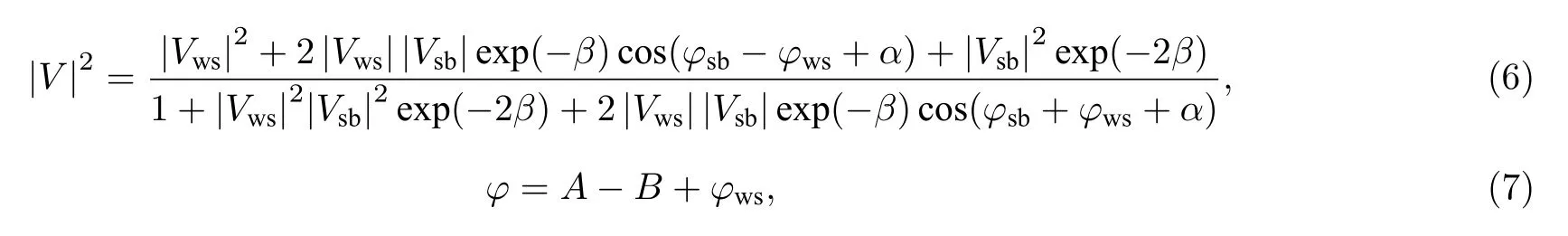
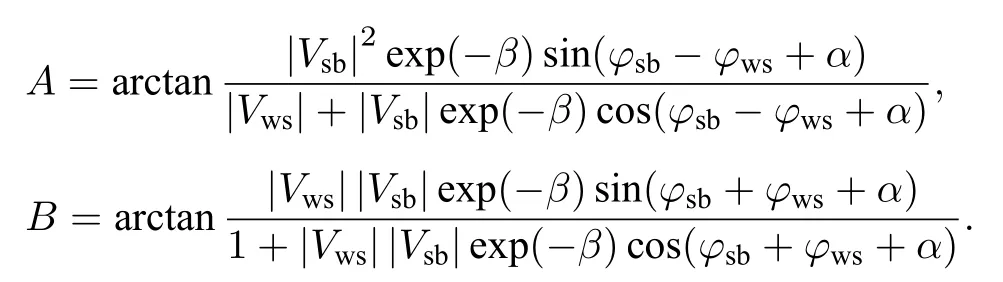
但表达式(5)只是形式上的,无法利用该表达式定量分析介质存在吸收时,入射声波的频率、角度及介质参数如何影响反射系数,因为此时的介质吸收系数掺杂在(5)式的各项中.在利用海底反射系数进行地声反演的角度,讨论分析介质存在吸收下的海底反射系数与各介质参数的敏感性是有必要的.吸收介质下的两层海底模型反射系数表达式推导见附录A.
3 海底吸收系数对海底反射系数的影响
除吸收系数外的地声参数对海底反射系数的影响,前人已进行了仔细的讨论分析,本文着重分析吸收系数对海底反射系数的影响.因引入的沉积层吸收系数与(6)式的各子项都有关,所以着重分析沉积层吸收系数的影响.
(6)式仿真参数如下:入射角为45°;海底海水声速cw为1515 m/s,密度ρw为1 g/cm3,满足大掠射角条件;入射频率为50 Hz—1 kHz.其余仿真参数在表1 给出.
考虑沉积层垂直相移满足半波层条件:
在不考虑介质吸收时,(1)式满足半波层条件时,仅与入射声波的入射角、频率以及沉积层声速和厚度有关.而考虑吸收时,(6)式同样具有这两种特殊情况,此时来源于(6)式的干涉项

与不考虑吸收的(1)式不同,此时干涉项的贡献不仅来源于沉积层中的垂直相移的实部,还与海水-沉积层界面、沉积层-基底界面的反射系数相位有关.
沉积层声速和厚度对入射声波的干涉周期影响是明确的,但在引入介质吸收后,吸收系数对干涉周期的影响并不明确.介质吸收与入射声波频率有关,因此给出(6)式干涉项中的两个界面的反射相位φws,φsb和沉积层垂直相移的实部α随入射频率和沉积层吸收系数的变化,以此分析吸收系数是否影响着干涉周期,以及干涉项的主要贡献的来源.仿真结果如图2 所示.
从图2 可知,在相同的参数范围内,φws,φsb的变化量要远远小于α.此时φws,φsb对干涉项(9)式的贡献远远小于α.


图2 各项参数随频率和沉积层吸收系数的变化 (a) 海水-沉积层界面反射系数相位;(b) 沉积层-基底界面反射系数相位;(c) 垂直相移实部Fig.2.Various parameters vary with frequency and the absorption coefficient of the sedimentary layer:(a) Phase of the reflection coefficient of the seawater-sedimentary layer interface;(b) phase of the reflection coefficient of the sedimentary layer-substrate interface;(c) real part of the vertical phase shift.
干涉项的主要贡献来源于α,同时可以观察到沉积层吸收系数并不影响干涉周期,影响干涉周期的是入射频率、入射角以及沉积层的声速和厚度.
此时,假设获取了不同入射角度下海底反射系数的干涉周期,建立(11)式所示的代价函数,用穷举法反演沉积层的声速和厚度:
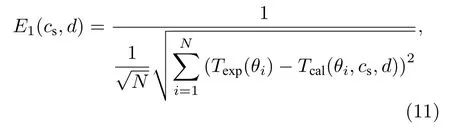
其中,Texp为实测数据提取的海底反射系数干涉周期,Tcal为利用(8)式计算的干涉周期,N为提取的干涉周期对应海底入射角的个数.
由于引入介质吸收,此时海水-沉积层界面、沉积层-基底界面的反射系数模|Vws|和|Vsb|,也与沉积层吸收系数有关.给出界面反射系数的模随入射频率和沉积层吸收系数变化的结果,如图3 所示.
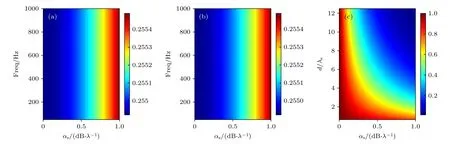
图3 各项参数随频率和沉积层吸收系数的变化 (a) 海水-沉积层界面反射系数模;(b)沉积层-基底界面反射系数模;(c) 衰减项Fig.3.Various parameters vary with frequency and the absorption coefficient of the sediment layer:(a) Reflection coefficient of the seawater-sedimentary layer interface;(b) reflection coefficient of the sedimentary layer-substrate interface;(c) attenuation term.
从图3(a)和图3(b)可知,|Vws|和|Vsb|与入射频率无关,随着沉积层吸收系数的增大,|Vws|略微增大,|Vsb|略微减小,但变化范围较小,可以认为界面反射系数的模项与沉积层吸收系数无关.对于基底的吸收系数,也可以得到类似结论,即可认为沉积层-基底界面反射系数模与基底的吸收系数无关.衰减项来源于沉积层垂直相移的虚部β,由于衰减项体现的是沉积层对入射声波的吸收,此时不仅与频率和沉积层吸收系数有关,还与沉积层厚度有关,为方便讨论,图3(c)纵坐标为层厚与入射声波波长比值.由图3(c)可知,在频率和沉积层吸收系数的参数范围内,衰减项的变化剧烈,说明吸收系数对(6)式中与衰减项有关的子项幅值大小有着重要影响.当沉积层厚度过大或入射频率过高时,衰减项接近于0.
图4 给出海底反射系数模随入射频率和沉积层吸收系数变化的结果.可以看出,由于沉积层吸收系数对海底反射系数的模随频率变化的振荡周期没有影响,在低频和沉积层吸收系数较小的情况下,海底反射系数呈现了稳定的振荡结构.但随着频率的增大,衰减项对海底反射系数的幅值影响逐渐明显,此时振荡结构逐渐消失,当频率过高时,海底反射系数等同于海水-沉积层界面的反射系数,为一常数值,即认为入射到沉积层内的声波能量被吸收殆尽.
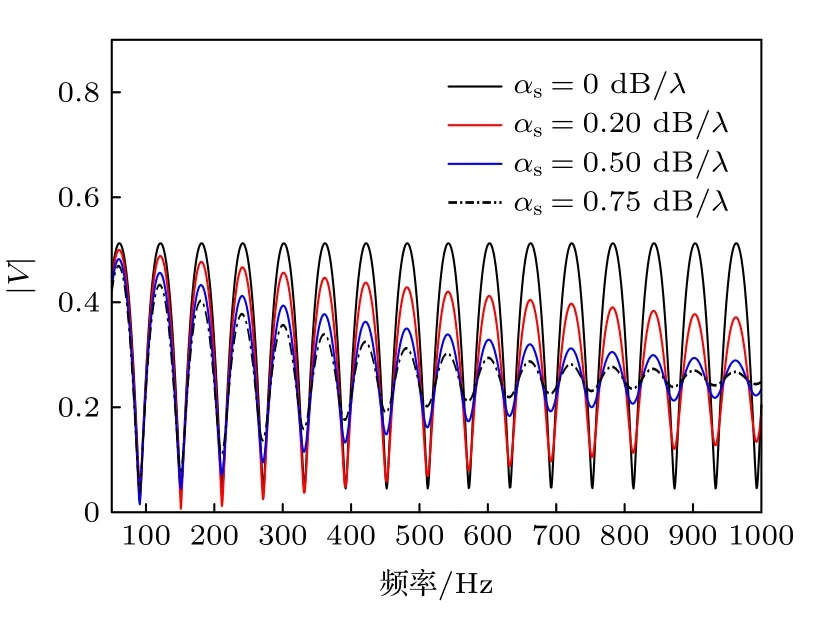
图4 海底反射系数模随频率和沉积层吸收系数的变化Fig.4.Seabed reflectance varies with frequency and absorption coefficient of sedimentary layer.
此外,图4 表明,(6)式的衰减项对海底反射系数幅值影响相对明显的是海底反射系数随频率振荡的极大极小值位置.考虑频率满足(8)式时,海底反射系数的模为如下形式:

可认为频率满足半波层条件时,对应的海底反射系数对沉积层吸收系数是敏感的.
从图4 可以看出,当频率位于半波层和1/4 波层间时,沉积层吸收系数对海底反射系数基本无影响,海底反射系数等于沉积层表面反射系数.此时干涉项数值上满足以下条件:
纳入标准:(1)均为接受产前检查的孕妇;(2)参与本次研究的孕妇,研究人员应与其讲述本次研究的全部过程,同时孕妇家属应在场,对于本次研究的全部过程清除了解后,孕妇属于自愿参与,并签署知情同意书;(3)孕妇的意识清晰、表达能力优良、精神状况佳;(4)ECGO评分处于0~1分。

将该条件定义为1/4 振荡周期频率,频率满足该条件时海底反射系数的模等同于海水-沉积层界面的反射系数模.此时,对应的物理意义为透射入沉积层的声波与基底界面反射的声波发生干涉相消,除沉积层表面反射及透射到基底的声波外,其余经基底反射的分裂波都被抵消了.当频率满足1/4 振荡周期频率条件时,将沉积层吸收系数、基底地声参数对海底反射系数的影响从模转移到频率间隔上,即所有的地声参数都影响着1/4 振荡周期频率的频点位置,此时各地声参数对海底反射系数的影响出现了不同.
取图4 中沉积层吸收系数为0.2 dB/λ下的海底反射系数,取其1/4 振荡周期频率523 Hz 分别计算海底反射系数随沉积层吸收系数、基底地声参数等的变化.同时给出相邻阶数的半波层频率542 Hz 和1/4 波层频率512 Hz 的结果,如图5 所示.
首先考虑半波层频率下,除基底吸收系数外,其余参数对反射系数的影响都较为明显.由(12)式可知,在半波层频率下,基底反射系数模和衰减项为主要贡献,即对应着基底地声参数和沉积层吸收系数.而由图3 可知,基底反射系数模基本不随沉积层和基底的吸收系数变化,所以反射系数不随基底吸收系数变化.
在1/4 振荡周期频率下,由于沉积层吸收系数体现了对声波的吸收,海底反射系数随着沉积层吸收系数增大而趋于海水-沉积层海底反射系数,且在参数范围内海底反射系数变化平缓,即认为海底反射系数基本不随沉积层吸收系数变化.在1/4 振荡周期频率下,海底反射系数随基底声速、密度增大而增大,虽然相比于半波层频率时变化幅度较小,但依然具有一定的敏感性.由此可见,基底声速和密度的改变对1/4 振荡周期频率位置的影响大于沉积层吸收系数.
结合图5 和上述分析,以海底反射系数幅值作为匹配参量时,有以下结论:
1) 在频率满足1/4 振荡周期频率条件时,可认为基底声速和密度敏感性大于沉积层和基底的吸收系数;
2) 在频率满足半波层频率时,相比于其他参数,沉积层吸收系数更为敏感.
3) 相比于其他参数,基底吸收系数基本不影响海底反射系数,可将其假设为经验值.
4 反演方法构建
假设利用(11)式获得沉积层声速、厚度后,并通过Hamilton 经验公式获得沉积层密度,那剩余待反演的地声参数分别为沉积层吸收系数、基底声速、密度和吸收系数.实现分步优化,线性反演地声参数,必须利用海底反射系数在不同条件下,与地声参数敏感性差异进行反演参数降维.从第3 节的结论可知,可利用海底反射系数在1/4 振荡周期频率和半波层频率下,地声参数的敏感性差异进行待反演参数的降维.
Hamilton 经验公式[22]为
首先对基底声速和密度进行反演.由于基底吸收系数始终对海底反射系数不敏感,假设为经验值1.0 dB/λ.利用海水-沉积层界面反射系数模提取了实测海底反射系数的1/4 振荡周期频率.计算出1/4 振荡周期频率下,随沉积层和基底的吸收系数变化的平均海底反射系数模,该均值对应的沉积层吸收系数参与反演基底声速和密度,如图5 注释点所示.图5 标注的仿真假设值和平均值几乎一致,进一步说明在1/4 振荡周期频率下将吸收系数设置为常数是合理的.在实际反演中,无法知道基底声速和密度的具体值,需要在基底声速和密度穷举的上下边界来计算吸收系数的均值.
此时,在1/4 振荡周期频率下,基底声速和密度参数范围内:

可认为实测获得的频域海底反射系数带宽内有M个用于反演的频点:
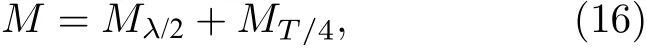
其中,Mλ/2为半波层频率的个数,MT/4为1/4 振荡周期频率的个数.
在1/4 振荡周期频率时,认为海底反射系数模仅与基底的声速和密度有关.构造以下代价函数:
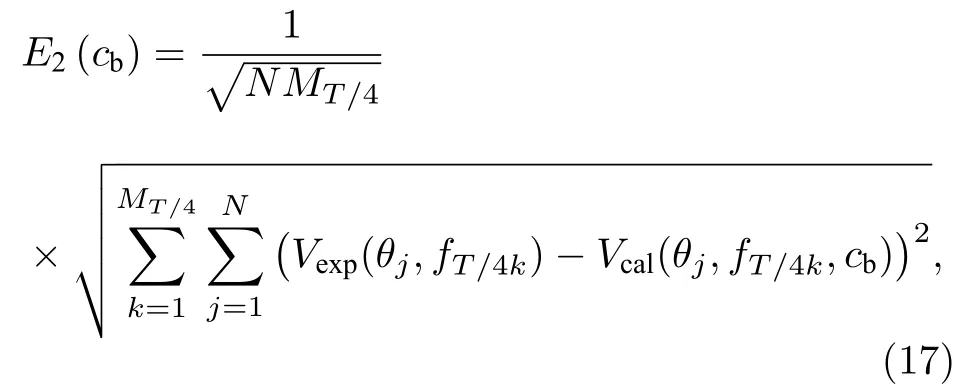
其中Vexp和Vcal分别是实际测量和模型计算的反射系数,基底密度由Hamilton 经验公式获得.
通过(17)式获得基底声速和密度后,对沉积层吸收系数进行反演.在半波层频率时,反射系数对沉积层吸收系数敏感,因此利用半波层频率下的反射系数对沉积层吸收系数进行反演效果更佳.此时的反射系数仅与吸收系数有关,一维寻优过程,吸收系数的敏感性不言而喻.构造以下代价函数:

在前人的研究中,也曾将吸收系数设为常数而进行待反演参数的降维,但给出的解释基本认为海底作用次数较少导致吸收系数的影响不大,可以认为是某一常数值.本文从不同吸收系数下反射系数随频率的振荡变化进行解释,定量地分析了在1/4振荡周期频率下将吸收系数假设为常数更为合理,并给出了吸收系数假设值的计算方法.
根据上述提出的反演模型,建立反演方案如图6.

图6 反演流程图Fig.6.Flow chart of inversion.
5 实验验证与分析
5.1 实验介绍
2021 年5 月,中国科学院声学研究所声场声信息国家重点实验室在东印度洋北部海域进行了一次深海声学综合实验.实验中使用“实验1”号科考船进行了声传播测量,并同步开展温盐深的同步测量.声传播实验采用单船走航式作业方式,使用宽带爆炸声源发射声信号,利用垂直阵接收声信号.实验设备布设如图7 所示.
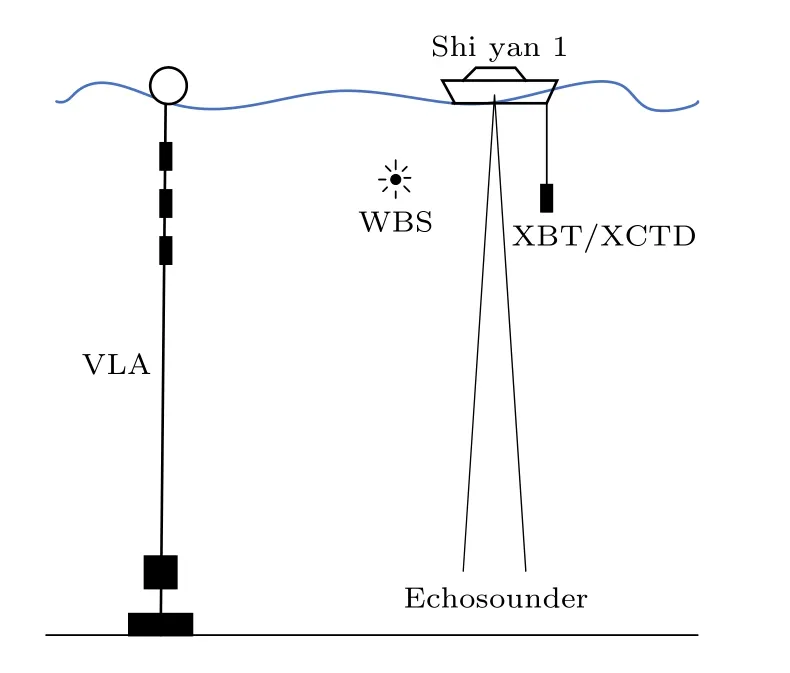
图7 实验作业方式示意图Fig.7.Schematic diagram of experimental work.
垂直阵由34 个分布在不同深度上的水听器单元组成,覆盖了38—3087 m 的深度范围.水听器灵敏度为—170 dB,单通道采样频率为16 kHz.发射船实验1 号沿测线航行,过程中交替投放50和200 m 的定深爆炸声源.走航的实验海域平均海深约为3100 m,总测线长度约为180 km,为满足本文方法大掠射角的条件,选取6 km 以内的实验数据进行深海地声参数反演.图8 为在接收阵附近使用CTD 测量并利用历史数据延拓至全海深的声速剖面,可见实验海区为典型的不完全深海声道.

图8 实验海区声速剖面Fig.8.Sound speed profile of the experimental sea area.
由于提取海底反射系数需要将各种多途信号分离,利用射线模型Bellhop 对实验海区前10 km接收的信号进行时延分析.图9 为声源深度200 m,接收距离为1.7 km 时的多途信号的时延值.可观察到明显的多途信号为直达波D、海面反射S、海底反射B,海面-海底发射SB 等.在接收深度300 m处,B 与SB、BS 以及SBS 的时延值出现交叉现象,不利于分离海底反射信号.本文选取了397—2000 m 的多途可分离接收信号进行海底反射系数的提取.
图10 为声源深度200 m,接收距离1.7 km,接收深度800 m 的水声多途信号,多途信号的相对时延值与图9 基本一致.
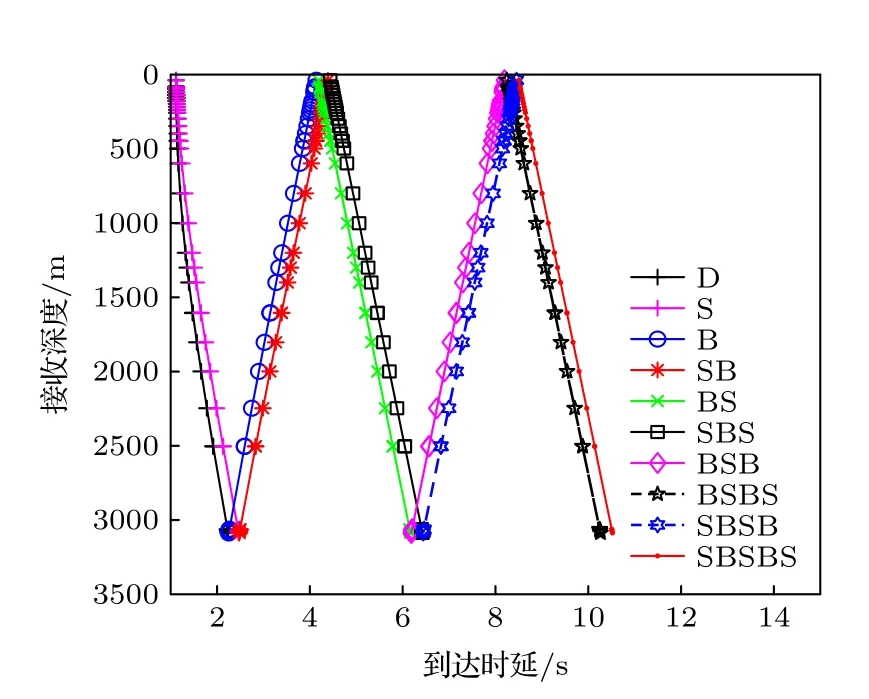
图9 声源深度200 m,接收距离1.7 km 的多途到达时延Fig.9.Multi-path arrival delay at source depth of 200 m and receiving distance of 1.7 km.
5.2 海底反射系数的提取
经过一次海底反射后到达的声压幅度Prb满足[23]:
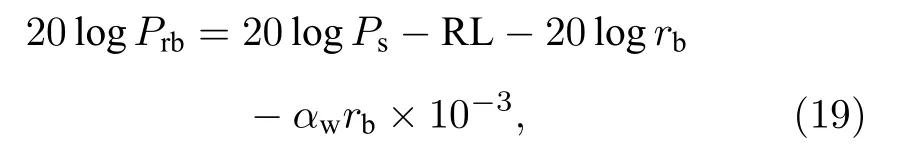
其中 R L 为海底反射损失(提取的 R L 包括(1)式中由沉积层-基底界面反射的能量);Ps为声源级声压幅度;rb(m)为一次海底反射声波传播的距离,由射线模型计算获得;海水吸收系数
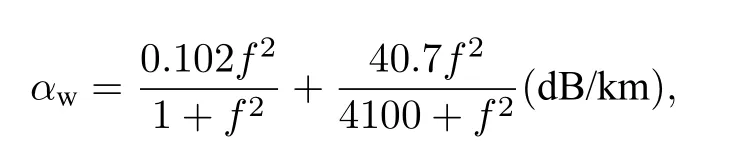
其中f(kHz) 为发射信号频率.获得海底反射损失后,转化为海底反射系数的模,为
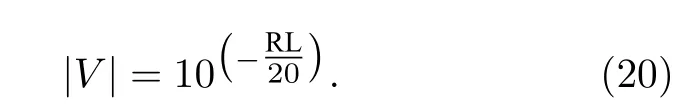
在实际海试中,获取的海底反射系数往往因为复杂的海底分层而导致振荡结构包含多个周期.由于本文方法假设海底为两层模型,所以需提取出反演频段内最主要的干涉周期,即对应实际海底最大的沉积层厚度,忽略其小的分层.从海底反射系数表达式(6)式可知,海底反射系数随频率的振荡来源于干涉项(8)式,所以构造以下函数与海底反射系数做相关,提取海底反射系数的干涉周期.
构造类似干涉项形式函数:
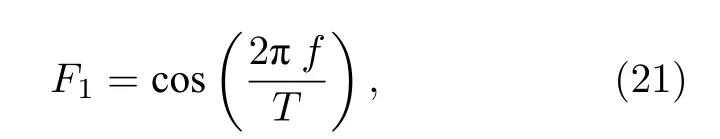
利用(21)式与频域海底反射系数做相关:
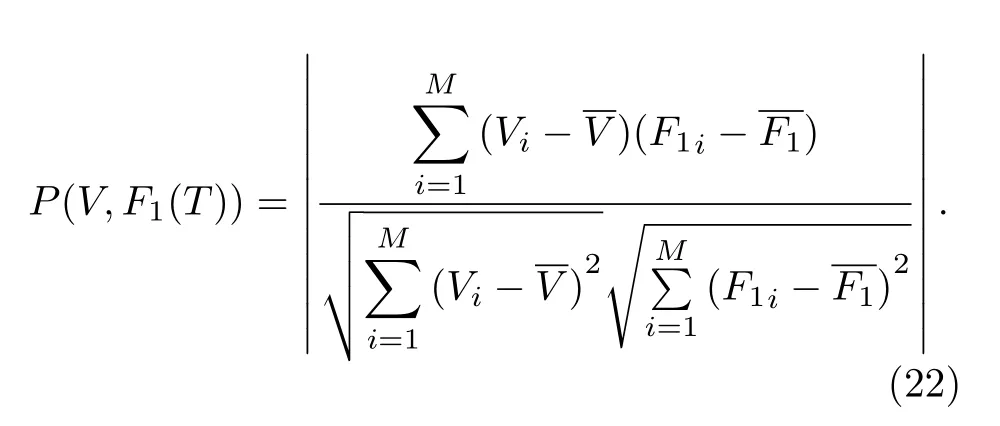
P(V,F1(T))为(21)式和海底反射系数的相关系数模,M为海底反射系数的频点数.当干涉周期T令P(V,F1(T))为最大时,T即为所需的干涉周期.
图11 为所有接收掠射角下的干涉周期提取结果,颜色轴数值大小代表(21)式与海底反射系数的相关系数,基本都在0.35 以上,具有较好的相关性.
5.3 深海地声参数反演
利用提取的干涉周期,结合代价函数E1反演沉积层声速和厚度,模糊度如图12.白色“+”号标记点标记为反演结果,沉积层声速反演结果为1570.6 m/s,厚度为2.4 m,利用 (14) 式反演得密度为1.61 g/cm3.从图12 可知,对于沉积层厚度而言,反演结果较为集中.即使利用多角度数据进行反演,沉积层声速和厚度依然存在一定的耦合.
利用第一步反演获得的沉积层声速和密度,提取海底反射系数的1/4 振荡周期频率,并以海底反射系数极大值为标准提取半波层频率,提取频点结果如图13 所示.在1/4 振荡周期频率下,计算各接收掠射角下基底声速穷举的上下边界对应的沉积层吸收系数均值,作为反演基底声速的沉积层吸收系数假设值.基底声速的穷举空间为1700—2200 m/s,沉积层吸收系数平均值如图14 所示,可以看出,假设的沉积层吸收系数此时与掠射角有关,这是因为不同掠射角下的1/4 振荡周期频率频点位置不同.
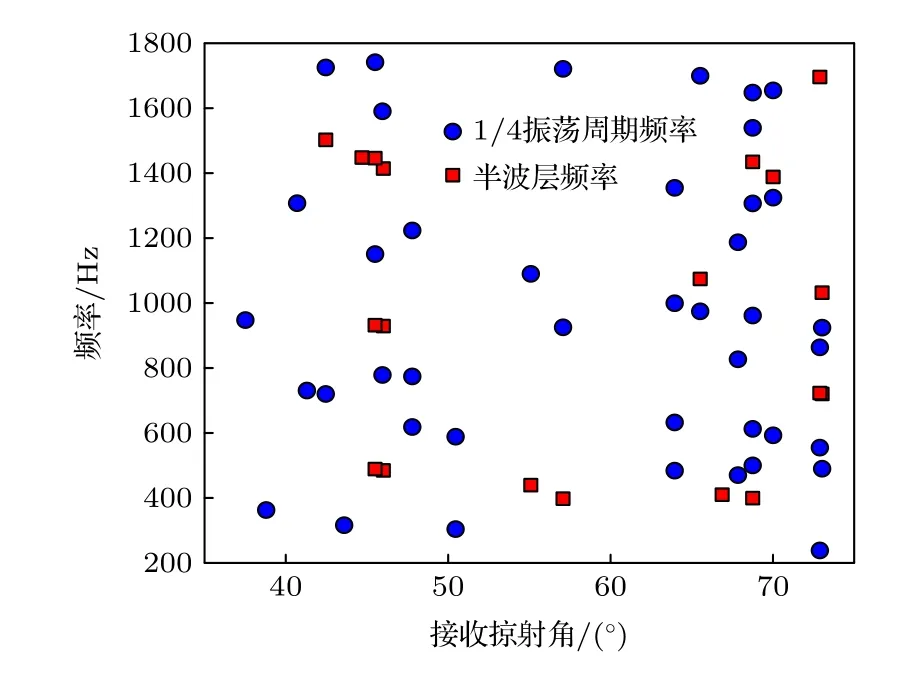
图13 提取海底反射系数的1/4 振荡周期频率和半波层频率Fig.13.1/4 oscillation period frequency and the half-wave layer frequency of seabed reflection coefficient.

图14 不同接收掠射角下对应的沉积层吸收系数平均值Fig.14.Average value of the absorption coefficient of the sedimentary layer under different receiving grazing angle.
利用代价函数E2结合沉积层吸收系数平均值,对基底声速进行一维反演,结果如图15 所示.虽然反演结果出现了多解现象,但代价函数最小值明显,基底声速反演结果为1809.5 m/s,(14)式计算的基底密度为2.06 g/cm3.
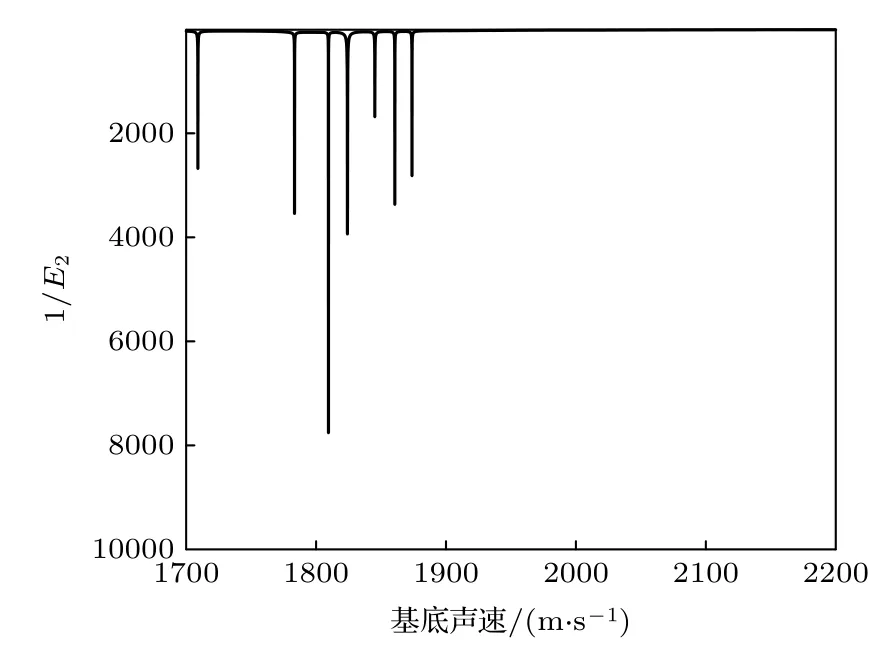
图15 基底声速反演结果Fig.15.Inversion result of the substrate sound speed.
最后,在半波层频率下,利用代价函数E3反演沉积层吸收系数,反演结果如图16 所示.在一维反演下,沉积层吸收系数得到了较为集中的结果,沉积层吸收系数反演结果为0.18 dB/λ.将沉积层吸收系数单位从dB/λ转化为dB/m,频率单位为kHz,有


图16 沉积层吸收系数反演结果Fig.16.Inversion result of the sedimentary layer absorption coefficient.
本文方法反演得到的沉积层吸收系数为多个频率反演下的均值,此时沉积层吸收系数(dB/m)与频率成线性关系.
图17 给出了单频下沉积层吸收系数的反演结果.当声波垂直波长大于沉积层厚度时,对声波起主要作用的是基底,本文对基底的吸收系数假设仅为经验值,错误的假设以及沉积层、基底地声参数之间的耦合,将会导致反演得到的沉积层吸收系数偏大;而当声波垂直波长小于等于沉积层厚度时,对声波起主要作用的是沉积层,此时不同频率下的反演结果围绕均值浮动,该均值为0.18 dB/λ.
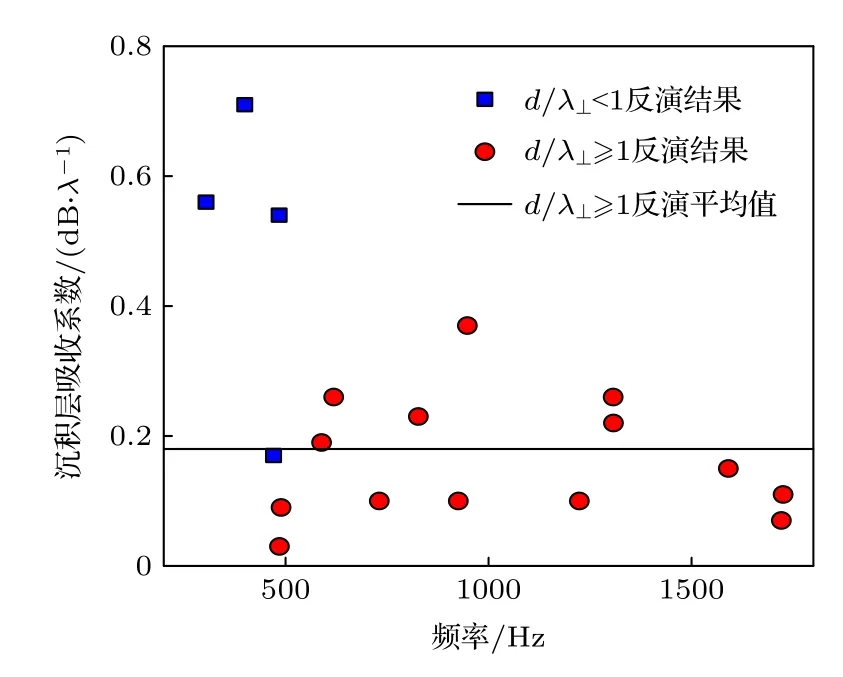
图17 单频沉积层吸收系数反演结果Fig.17.Inversion results of sedimentary layer absorption coefficient under single frequency.
对于海底反射系数幅值而言,沉积层吸收系数和基底声速之间存在耦合.沉积层吸收系数估计结果偏大时,导致衰减项偏小,基底阻抗的估计结果可以偏大,使得沉积层-基底界面的反射系数偏大,来平衡衰减项对海底反射系数幅值的影响.单纯假设沉积层吸收系数反演基底声速使得结果并不可信.因此,有必要讨论1/4 振荡周期频率和半波层频率下,沉积层吸收系数和基底声速的耦合程度差异.
图18 和图19 给出了两种频率条件下,利用(24)式对沉积层吸收系数和基底声速进行二维反演的模糊度图,白色“+”号为反演结果,并对代价函数值进行了归一化.前人利用海底反射系数进行多维地声反演的目标函数为其中m为待反演的参数向量.为方便讨论,这里的m仅包含沉积层吸收系数和基底声速两项,M为频点个数.
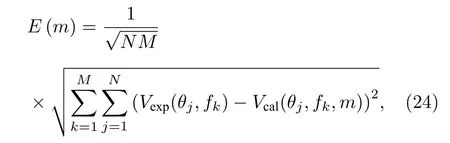
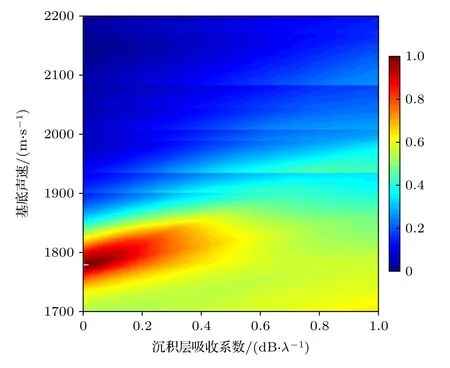
图18 1/4 振荡周期频率下沉积层吸收系数和基底声速的二维反演结果Fig.18.Two-dimensional inversion results of absorption coefficient of sedimentary layer and sound speed of substrate at 1/4 oscillation period frequency.

图19 半波层频率下沉积层吸收系数和基底声速的二维反演结果Fig.19.Two-dimensional inversion results of absorption coefficient of sedimentary layer and sound speed of substrate at half-wave layer frequency.
从敏感性来看,半波层频率下海底反射系数对沉积层吸收系数和基底声速的敏感性要强于1/4振荡周期频率,而1/4 振荡周期频率下,基底声速的反演结果更为集中,海底反射系数对于基底声速的敏感性要强于沉积层吸收系数,这都与前文结论一致.从耦合程度来看,半波层频率下代价函数最大值从[0 dB/λ,1780 m/s]一直延伸至[0.7 dB/λ,1900 m/s],远大于1/4 振荡周期频率下的区域,说明半波层频率下沉积层吸收系数和基底声速的耦合程度更强.
该结果原因在于(12)式与(13)式.当频率满足半波层频率时,基底反射系数和衰减项影响着反射系数的模,而频率满足1/4 振荡周期频率时,基底反射系数模和衰减项影响着频点位置.在相同参数范围内,海底反射系数模的变化量远大于频点的位置变化量;在1/4 振荡周期频率下,由于沉积层吸收系数的取值基本不影响海底反射系数的模,起主要贡献的为基底反射系数模.
图18 的反演结果为沉积层吸收系数0.01 dB/λ,基底声速为1779 m/s,图19 反演结果为0.04 dB/λ和 1787 m/s.沉积层吸收系数反演结果掉落在穷举边界,一方面是因为1/4 振荡周期频率下海底反射系数对沉积层吸收系数的不敏感,另一方面是因为两种频率条件下,沉积层吸收系数和基底声速都有着不同程度的耦合,二维反演难以获取沉积层吸收系数可信的结果.
综上,1/4 振荡周期频率下沉积层吸收系数和基底声速的耦合程度更低,将沉积层吸收系数进行合理假设对基底声速的反演结果影响较小,在1/4振荡周期频率下假设沉积层吸收系数具有一定的解耦合意义,且一维反演过程更有利获取准确的反演结果.
本文方法反演的地声参数结果如表2 所列.由于在实验过程中未进行底质采样,无法利用采样验证反演结果,因此利用Hamilton[23]总结的沉积物分类结果以及反演得到的地声参数进行传播损失计算与实验值对比,以作反演结果的验证.Hamilton分类结果如表3 所列.
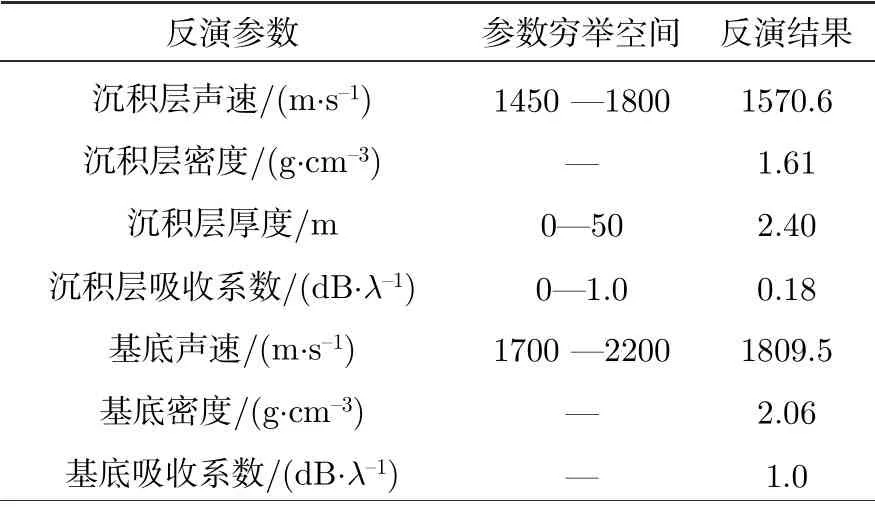
表2 本文方法反演结果Table 2.Inversion results obtained by using the method in this paper.
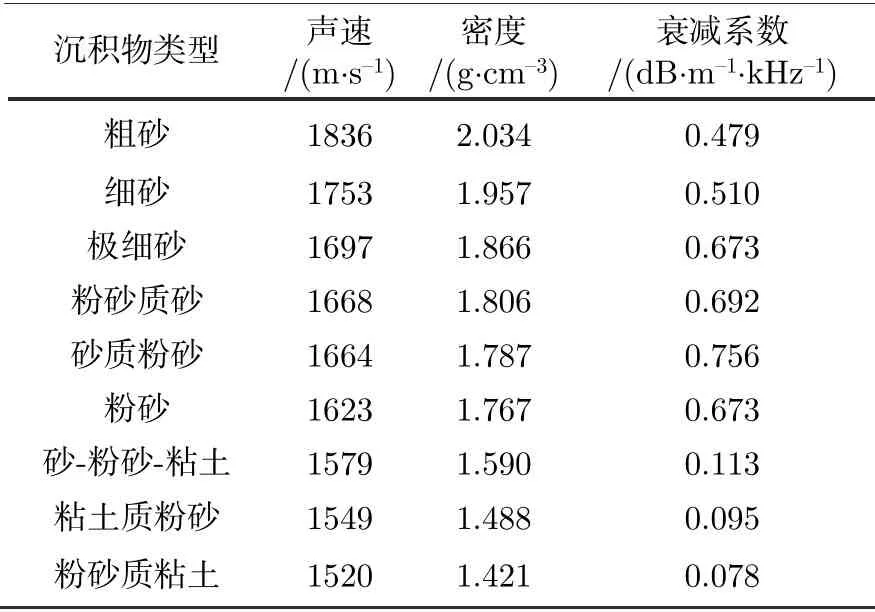
表3 Hamilton 沉积分类参数Table 3.Hamilton sedimentary classification parameters.
因为本文利用Hamilton 经验公式反演密度,所以仅从声速和衰减系数的反演结果分析.本文沉积层声速反演结果为1570.6 m/s,对应表3 沉积层类型为砂-粉砂-粘土,衰减系数为0.113 dB/(m·kHz),与本文反演结果0.1146 dB/(m·kHz)接近.
计算声源深度200 m,接收深度为垂直阵水听器分布深度,中心频率分别为800 Hz,1 kHz,1.2 kHz,1/3 倍频程下的传播损失.图20—图22 给出部分接收深度和中心频率的传播损失以及不同接收深度下传播损失均方根误差.图20 还给出了图19 中反演结果的传播损失.
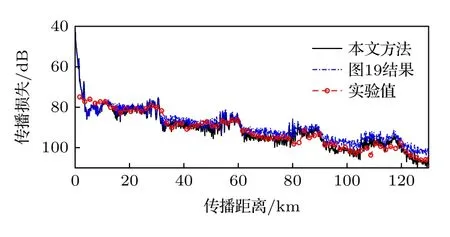
图20 声源深度200 m,接收深度97 m,中心频率1 kHz时的传播损失Fig.20.Transmission loss at source depth of 200 m,receiving depth of 97 m and center frequency of 1 kHz.
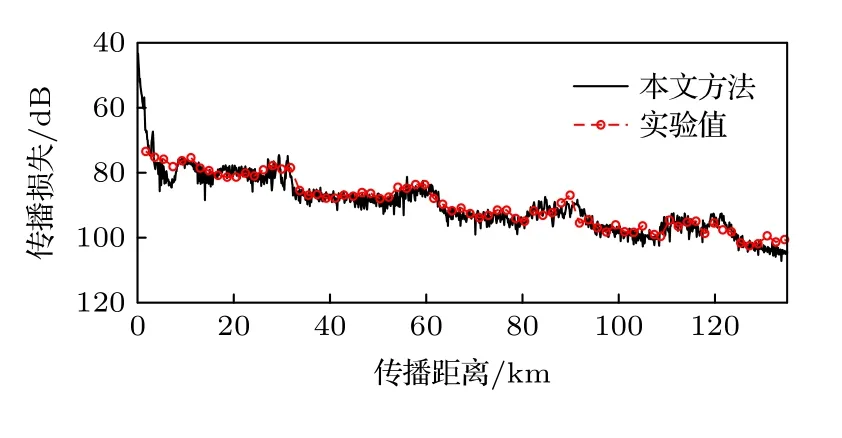
图21 声源深度200 m,接收深度97 m,中心频率800 Hz时的传播损失Fig.21.Transmission loss at source depth of 200 m,receiving depth of 97 m and center frequency of 800 Hz.
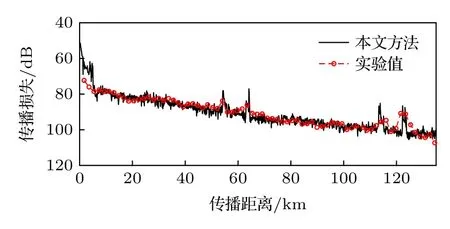
图22 声源深度200 m,接收深度598 m,中心频率1.2 kHz时的传播损失Fig.22.Transmission loss at source depth of 200 m,receiving depth of 598 m and center frequency of 1.2 kHz.
从图20—图22 来看,本文方法反演结果的传播损失理论值与实验值总体上在100 km 前符合较好,误差主要出现在直达波区和会聚区,而影区的传播损失符合较好.直达波和海面一次反射的能量相比于海底反射能量较大,底质反演结果对传播损失的影响较小.考虑到声速剖面、相对距离、收发深度有可能存在测量误差,导致前三个距离点上的传播损失符合较差.
就整体而言,本文方法反演的海底参数可以给出相对符合的传播损失结果.本文所使用的数据在不完全声道下实验获得,声场能量主要由海底反射为主,即使较远距离下的传播损失依然受海底的影响.结果显示远距离下的传播损失依然符合较好,说明本文反演的地声参数能较为有效地描述该实验海区的海底特征.但对于其他实验海区,近距离反演的结果是否能适用于较远距离的传播损失预报,还需通过实验验证.
图20 中,随着传播距离的增大,声波经海底多次反射,沉积层吸收系数的影响明显,图19 给出的反演结果显得不可靠,而本文方法反演的结果与实验数据更符合.图23 和图24 分别给出了不同接收深度下,传播距离为前180 km 和前100 km的传播损失均方根误差,可以看出,前180 km 时均方根误差大于前100 km 时,100 km 前的传播损失均方根误差主要分布在2.5—4.0 dB.随着接收深度的增大,均方根误差增大.
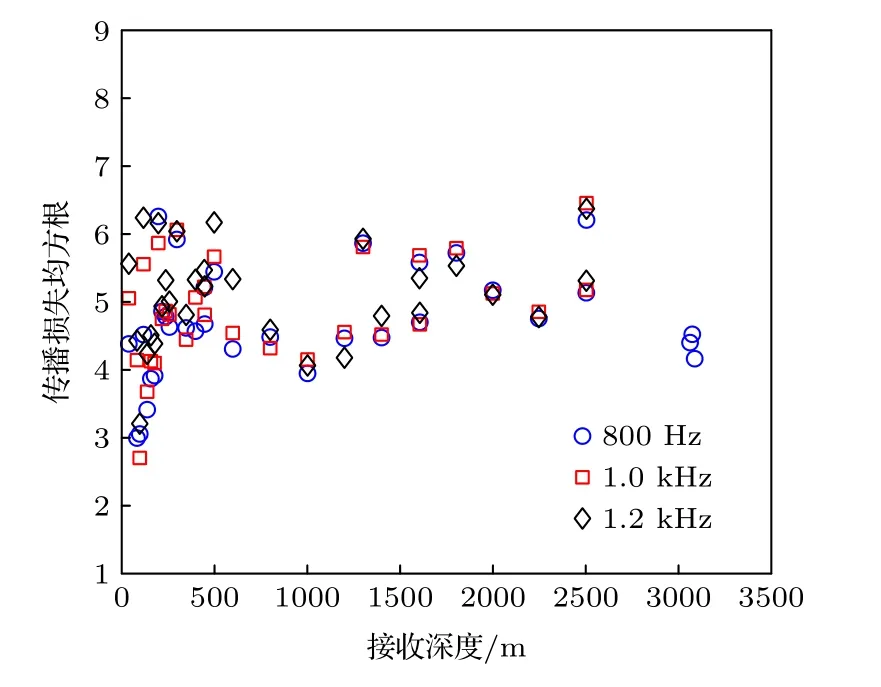
图23 不同接收深度下前180 km 传播损失均方根误差Fig.23.RMSE of transmission loss of 180 km at different reception depths.
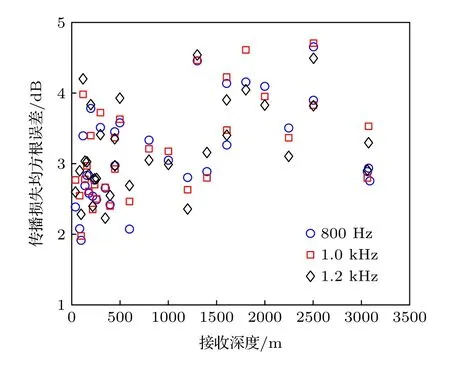
图24 不同接收深度下前100 km 传播损失均方根误差Fig.24.RMSE of transmission loss of 100 km at different reception depths.
综上,本文方法反演的地声参数可以有效预报一定传播距离内不同接收深度、不同频率的传播损失.
6 结论
针对利用海底反射系数反演深海地声参数问题,通过推导分层吸收介质下的海底反射系数表达式,着重分析了大掠射角下沉积层吸收系数对(6)式各子项的影响,并发现在1/4 振荡周期频率下,沉积层吸收系数基本不影响海底反射系数模的现象.利用这一特性,结合分步优化策略,本文提出了一种深海地声参数线性反演方法.通过在1/4振荡周期频率对沉积层吸收系数做出合理假设,结合分步优化和一维反演,实现强耦合参数(沉积层吸收系数、基底声速)较为准确的获取,在一定程度上实现了沉积层吸收系数与基底声速的解耦合.利用2021 年印度洋实验获得的宽带声传播信号进行反演的结果,表明了该反演方法在大掠射角测量条件下反演的深海地声参数,可有效应用在一定范围内的传播损失预报.
诚挚感谢2021 年东印度洋航次全体科考人员的辛勤作业,让本文能拥有可靠的实验数据以作方法验证.
附录 A
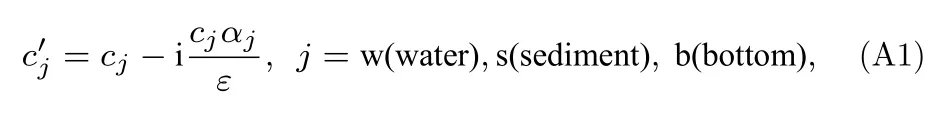
其中cj和αj分别为介质的声速(m/s)和吸收系数(dB/λ),ε为一常数,ε=2π×8.686 .
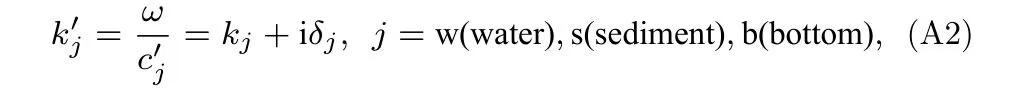
其中
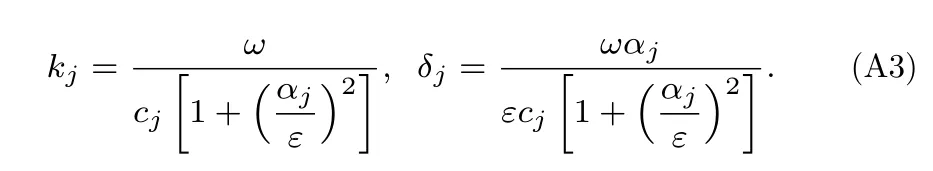
在正入射下,各介质声阻抗率为
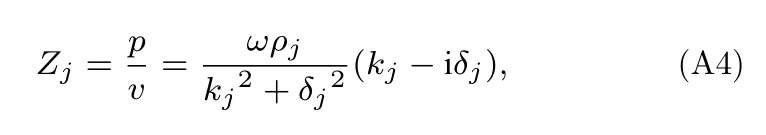
考虑水中声波入射角为θw,且有边界水平波数相等:
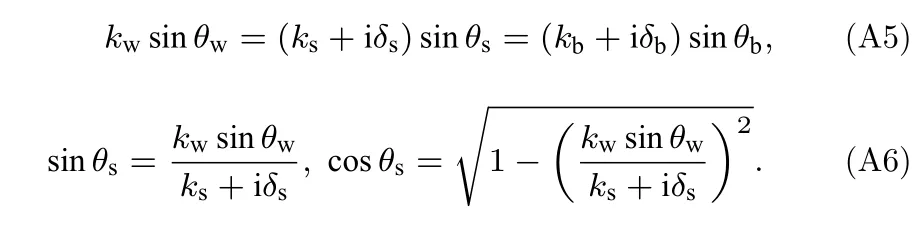
至此,由于引入了介质吸收系数,此时无论是吸收介质的波数还是对应的折射角都为复数形式,即使水中入射角为实数.
沉积层法向声阻抗率为

化简得

将Zss实部与虚部分离:
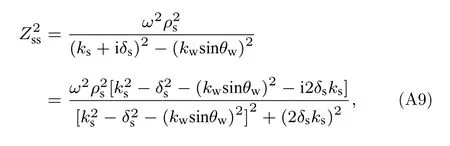
令
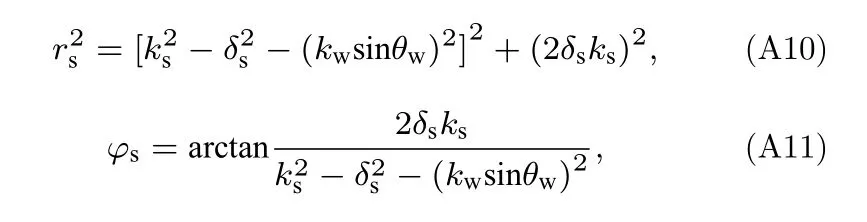
即
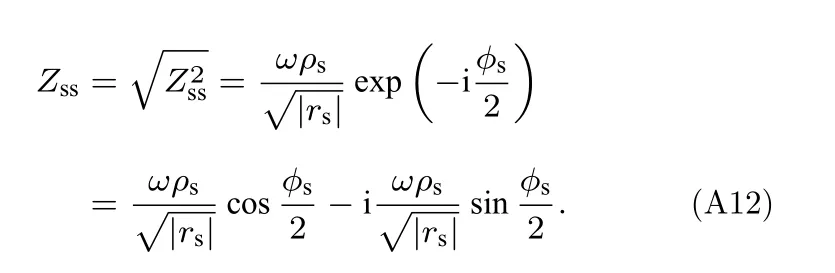
以此类推,基底的法向声阻抗率为
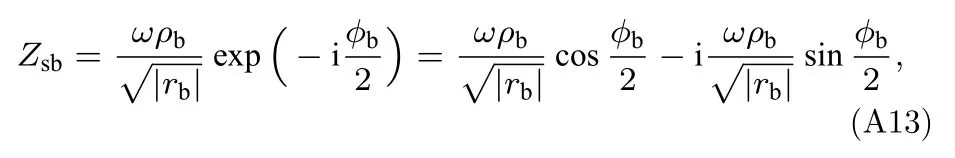
对于沉积层中的垂直波数,可以表示为
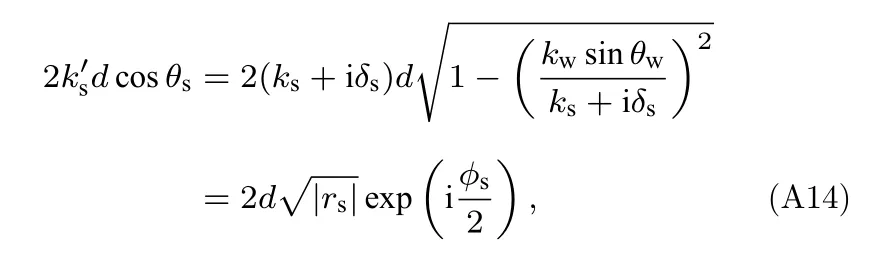
将实虚部分离,并令
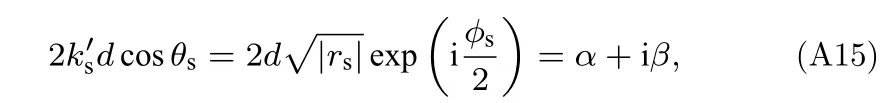
所以
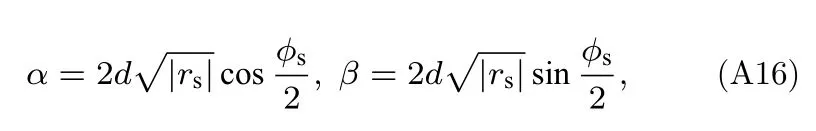
其中α和β分别为沉积层垂直波数的实部和虚部.(A15)式表明,在考虑存在吸收时,沉积层的垂直相移不仅与沉积层厚度、声速有关,还与沉积层的吸收系数有关.
将(A12)式—(A16)式代入(6)式得:


