结合相关系数及改进层次分析法的油浸式变压器质量评估
云玉新,赵富强,张 磊,秦佳峰,陈新岗,谭 悦,朱莹月
(1.国网山东省电力公司电力科学研究院, 济南 250003;2.重庆理工大学 电气与电子工程学院, 重庆 400054)
0 引言
随着我国电网技术的不断发展,油浸式变压器因独有的优势在整个电力系统中得到了越来越广泛的应用[1]。在对变压器质量和运行工况的评估中,较长时间内都是通过定期检修、电气试验、停电预防性试验、油色谱分析来实现。这一系列试验都有相应的标准,但只能反映某试验中的指标是否达标。目前,国内外的研究也较多将重点聚焦于静态、定量的基于部分指标的评估分析方法[2-4]。
在油浸式变压器质量评估中,对试验数据的分析是必不可少的一个环节[5]。徐振乙等[6]和王英洁等[7]利用试验数据构建评估数据库,根据国家电网的相关标准及评价导则对各项指标进行合格判别,但没有深入挖掘各类数据之间的关联关系,没有一套综合的评估模型;云玉新等[8]和李连结等[9]采用组合赋权对评估对象的各项指标进行权重分配,但其中2种赋权方法的权重值在融合时没有考虑各自的比例系数,也未充分结合2种赋权方法的优势;张海瑞等[10]采用反熵权法进行评价,优化了熵值法因差异度灵敏性带来的指标极化问题;付学谦等[11]运用理想解法对评估对象进行排序,具备一定参考性,但没有对电能质量等级进行明显的划分;刘晋芳等[12]的研究考虑了各指标的不同影响程度,但存在一定的主观性,没有充分利用数据的客观性。因此,在对变压器进行质量评估时,要从全局和系统的角度出发,充分考虑各个指标的影响程度,并考虑指标数据的极值、数据分布情况和整体恶化度。在进一步对各评估指标进行赋权时,既要考虑评估需求和目的,也要利用数据本身所具有的客观信息,以充分、有效地结合主、客观信息,构建油浸式变压器的质量检测评估模型。
综上,基于综合变权的层次分析法及相关系数对10~35 kV油浸式配电变压器进行质量评估。首先,对油浸式变压器的各类影响因素进行分析,确定评估指标体系,参考专家经验及国家电网各类物资质量的相关标准与评价导则,利用层次分析法(AHP)进行主观赋权;其次,利用反熵权法对油浸式变压器的试验数据与实际检测情况做定量和定性分析,进行客观赋权,根据2种方法的权值修正得到一个综合的可变权重,再结合相关系数,得到油浸式变压器各评估指标的重要性排序和内在关联关系;最后,根据建立的模糊评估模型对油浸式变压器的质量水平进行评估。质量评估流程如图1所示。
1 油浸式变压器评估指标体系
在配电变压器运行过程中,存在众多影响其质量水平且又相互关联的因素,这些因素间的关联程度互不相同,存在较大的不确定性和模糊性。因此,油浸式配电变压器质量评估指标的确定和整个评估体系的建立十分重要。
1.1 确定评估指标集
为了全面、系统、客观、真实地表征油浸式变压器的质量水平,在征求专家及现场运维人员意见的前提下,从油浸式变压器的运行可靠性、运行工况、固有电气特性和历史环境信息4个角度出发,选择了16种状态参量作为油浸式变压器质量水平的评估指标,其中包含实时检测数据、试验数据、历史运维信息和环境信息。
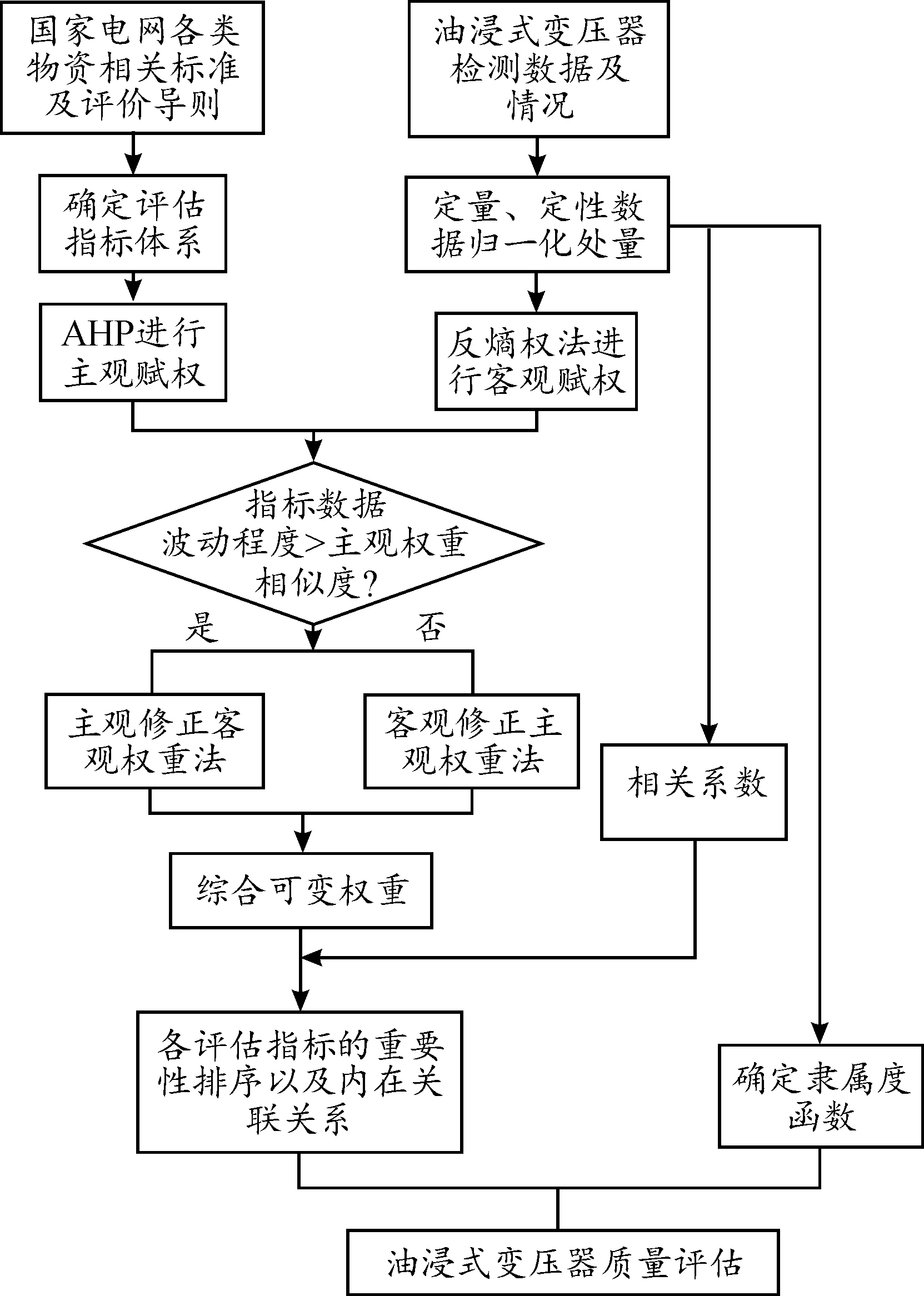
图1 质量评估流程框图
评估体系分为3个层级。顶层的目标层为油浸式变压器质量水平X,分解到中间准则层的4个评估子项目为X=(X1,X2,X3,X4),每个子项目又各自包含了4个评估指标,构成了底层的指标层。其中,感应耐压试验X11、外施耐压试验X12和故障检修记录X43为定性指标,其余13个指标为定量指标。最终建立的油浸式变压器质量评估指标体系如图2所示。
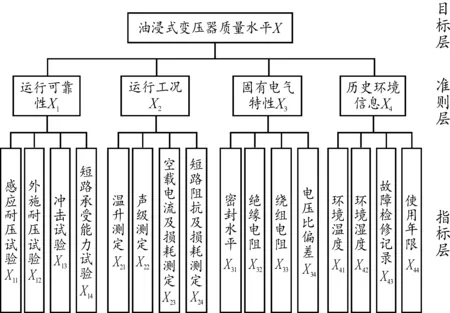
图2 油浸式变压器质量评估指标体系
1.2 评估等级划分
在油浸式变压器评估指标体系中,最终要对变压器的健康状况进行等级判别。综合实际情况和相关文献中的等级划分,将油浸式变压器的质量水平划分为良好、合格、异常、不合格4个等级,令评估等级集合U={U1,U2,U3,U4}[13-14]。U1为“良好”,代表变压器整体质量良好,能够安全稳定运行;U2为“合格”,表示变压器整体性能略微下降,但依然能够保证安全稳定运行;U3为“异常”,表示变压器质量情况不佳,存在一定的运行风险,应定期检修维护;U4为“不合格”,表示变压器已受损,某些指标无法达到国家标准,运行安全无法保证,需要立即进行检修。
2 油浸式变压器综合质量评估模型
油浸式变压器的质量水平不仅关乎其使用寿命,还影响整个电力系统的运行安全性和稳定性。进行配电变压器的质量评估时,需要准确描述具体工作状态和健康水平,而油浸式变压器质量评估指标的权重直接决定了最终结果的准确性,因此指标赋权方法的选取极为关键。
2.1 层次分析法确定主观常权
2.1.1因素间相对重要性判断矩阵的建立
根据图2中评估体系所确定的层次结构,每个元素与该元素所支配的下层元素构成一个子域,其中的所有元素构造若干判断矩阵[15]。构造矩阵的意义在于将上层元素支配的所有子层元素间相对重要程度进行定量分析。文中采用1~9比例标度法构建判断矩阵D,如表1所示。

表1 1~9比例标度法
2.1.2单层排序及一致性检验
根据矩阵论,各维度的权重对应判断矩阵D最大特征根λmax的特征向量,对其归一化处理后记为A。
DA=λmaxA
(1)
A矩阵各元素为相同层次中元素相对于上层级中因素较其余因素的相对重要性的排序权重,该过程也称层次单排序。此时还需对矩阵D进行一致性检验,表示为:
(2)
引入随机一致性指标fRI衡量一致性指标fCI,fRI由矩阵阶数n决定,本文中阶数为4,因此fRI=0.9。定义一致性比率fCR为两者的比值:
(3)
当fCR<0.1时,表示矩阵D通过一致性检验。
2.1.3总排序及一致性检验
为计算指标层中各因素相对于总目标层的权重,从而找出能够表征变压器质量水平的有效指标,还需进行总排序。准则层m个因素X1,X2,…,Xm对目标层X的排序记为a1,a2,…,am;底层n个因素对准则层中Xi的单层排序为b1j,b2j,…,bnj(其中j=1,2,…,m)。则底层指标对于目标层的权重即主观常权,表示为:
(4)
总排序的一致性比率fCR为:
(5)
同理,当fCR<0.1时,表示总排序的一致性检验通过。
2.2 反熵权法确定客观变权
熵体现了系统的无序程度,具体到指标层面则体现了数据的离散性和不确定性。熵值法是基于数据驱动的客观赋权方法。本文中采用反熵权法修正熵值法对指标从差异度敏感性不足的问题,当指标的数据差异性越大时,反熵越大[16-17]。
2.2.1指标数据预处理
上文中对油浸式变压器的质量评估所选取的指标特征分为定性和定量2种。对于定量指标,其数据拥有确定的数值;对于定性指标,则根据试验结果分配其值,合格为“1”,否则为“0”,再统一将所有指标的数值进行预处理。
对m个指标,相应有n个数据,则aij为指标层中第i个元素的第j个样本的数据(i=1,…,m;j=1,…,n)。对于存在最优特定值的指标,其标准化处理为:
(6)
式中:aov为该项指标最优值。
指标数据值越大代表该项试验情况越好的称为效益性指标(正指标),如绝缘电阻等,其标准化处理表示为:
(7)
指标数据值越小代表该项试验情况越好的称为成本性指标(负指标),如温升等,其标准化处理表示为:
(8)
2.2.2反熵权法
根据归一化后各项数据建立评价矩阵C,维数由指标决定。求出各项指标中数据所占比重后,可得该指标的熵为:
(9)
则修正后的反熵为:
(10)
最终得到权重为:
(11)
当指标数据发生变化时,基于数据驱动的权重也会随之改变。
2.3 确定综合可变权重
之前对变压器的质量水平的评估研究大多只选取了指标单一的主观权重、客观权重,或者仅为两者间简单的拟合,会导致最后的评估结果出现偏差[18-19]。组合赋权方法中使用最多的为线性组合,如下所示:
Zi=αWi+(1-α)Hi
(12)
由于线性组合过程中,对2种权重系数的确定依然是主观过程,为避免上述问题,考虑根据主客观权重偏差来对最终的综合可变权重进行修正。
2.3.1主观修正客观权重
将各评估指标中主观权重的极值分别定义为最大值wmax与最小值wmin,则主观修正客观权重的计算如下:
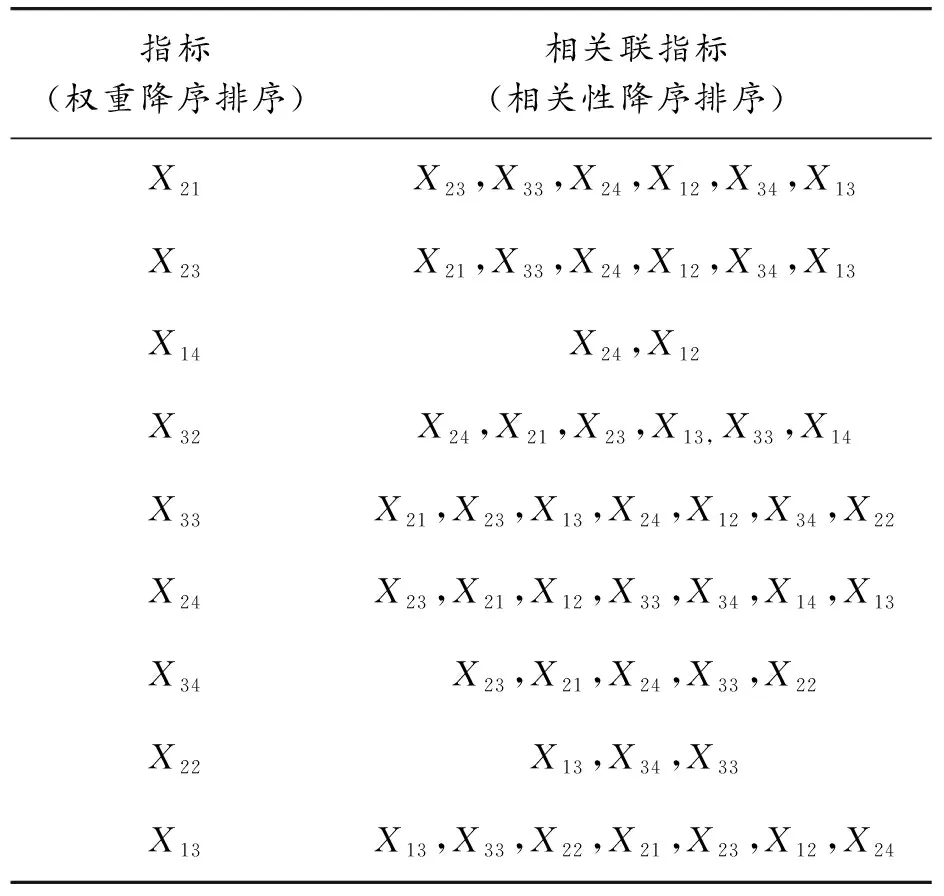
1) 若Hi (13) 2) 若Hi∈[wmin,wmax],则Zi=Hi。 3) 若Hi>wmax,则该项指标的综合权重Zi=wmax,其余指标的综合权重为: (14) 式中:k=i+1,i+2,…,n。 2.3.2客观修正主观权重 客观修正主观的综合权重时,将熵作为常规线性组合赋权的比例系数,具体表示为: (15) 上述2种修正法的具体选择方式:将所选的指标数据波动情况与主观权重相似程度进行比较,若指标数据中存在较大的波动情况,则利用主观修正客观权重;反之,选择客观修正主观权重,最终获得各个指标的综合可变权重。 为了探索多个指标间的关联关系,探索多指标数据间的相关性,可通过Person相关系数度量两变量间的相关程度[20]。由此,可以将Person相关系数用于探索多指标间的关联关系,表示为: (16) 式中:r为两试验指标间的Person相关系数;X、Y分别为各试验指标;下标k为指标数据组序列。r取值范围为[-1,1]。通常,当r取值在0.00~±0.30时,两指标相关程度为不相关;当r取值在±0.3~0.5时,两指标相关程度为微相关;当r取值在±0.50~±0.80时,两指标相关程度为显著相关;当r取值在±0.80~±1.00时,两指标相关程度为高度相关。本文中取多指标间相关程度为微相关及以上值,代表两指标间具有相关性。当计算出多指标间具有一定相关性后,在后期对油浸式变压器的检测中可按照各指标综合权重大小和与之相关联的指标、试验项目的排序优先对靠前列的项目进行检测,从而提高设备检测效率。 利用隶属度函数对油浸式配电变压器的质量评估做等级划分,通过将综合变权与隶属度函数计算出的模糊综合评判矩阵相结合,最终确定待测油浸式变压器的质量水平[21-23]。隶属度函数为: (17) (18) (19) (20) 将标准化后的指标数据依照划分区间分别代入相应隶属度函数中,所得评判矩阵为: Rn=[un1,un2,un3,un4] (21) 式中:n为准则层中的4个层次,即X1、X2、X3、X4。由此可以得到目标层的模糊综合评判集B为: Bn=WnRn=[b1,b2,b3,b4] (22) 式中:Wn为各准则层中各项指标的综合可变权重。利用所得集合代入式(23)中进行综合分值计算: (23) U值与变压器质量等级的对应关系如表2所示。根据表2,当U的取值范围在[1,2]时,油浸式变压器的质量水平处于正常状态,即合格,且值越靠近1说明质量水平越好;当U的取值在其余范围时,对应油浸式变压器的质量水平处于异常或不合格状态,U值越大说明质量水平越差。 表2 U值与质量等级的对应关系 为保证可靠性,本文中数据均来源于电网对油浸式变压器的相关试验和实际检测数据。 根据国家相关技术标准,考虑变压器常见故障类型,对应故障发生机率,同时征求一线运维人员及专家的意见,构造相应判断矩阵D为: 进一步得到其最大特征根λmax=4.118,对应特征向量。其一致性比率fCR=0.043<0.1,一致性检验符合要求。 同理,得到{Xi1,Xi2,Xi3,Xi4}关于Xi的判断矩阵。对应特征向量Bi(i=1,2,3,4)矩阵为: 对应最大特征根λi为[4,4.106,4.01,4.01],其一致性比率fCR均小于0.1,一致性检验符合要求。 由层次分析法得到的主观常权为: 代入数据得到由数据驱动的反熵权法的可变客观权重为: 将2种权重进行比较之后,选择主观修正客观权重法,可得各指标综合变权值的矩阵Z为: 将综合变权与相关系数相结合得到各指标的关联性(表3)。在油浸式变压器的质量检测中,应首先遵从“先进行特性试验、再进行破坏性试验”的原则,然后依据综合权重及相关程度大小,按顺序检测相应试验及指标是否正常[24-25]。 由表3中各指标按相关程度大小排序的结果可知:按照“先进行特性试验、后进行破坏性试验”的原则,同时根据权重顺序及相关性,可先进行温升试验(X21)的检测,再进行绕组电阻测试(X33)、空载电流及损耗测定(X23)、短路阻抗及损耗测定(X24)等试验的检测。当排行靠前的任一检验项目不合格时,可直接判定该变压器处于故障状态,从而极大缩减检测时间及一线检修人员的工作量。 表3 各指标间关联关系 将检测数据标准化后代入隶属度函数得出目标层的模糊综合评判集后,结合综合变权值,得到6台待测油浸式变压器的质量等级(表4)。其中,有5台变压器的质量水平介于良好与合格之间,1台变压器的质量呈现异常状态,与原始数据的实际检测结果一致。 表4 6台变压器质量等级划分结果 利用层次分析法(AHP)及反熵权法对油浸式变压器的试验数据与实际检测情况进行定量及定性分析,通过主客观赋权和相应权重的修正获取各指标最终的综合可变权重;结合相关系数得到油浸式变压器各评估指标的重要性排序和内在关联关系,按照“先进行非破坏性试验、再进行破坏性试验”的检测顺序,根据综合权重及相关程度,按顺序检测相应试验及指标是否正常,缩减检测时间和一线检修人员的工作量;通过算例验证了所建立的油浸式变压器质量评估模型的准确性。 本研究中对油浸式配电变压器的质量评估能体现该类变压器中各指标间的关联性,保证对油浸式配电变压器质量评估的有效性。2.4 指标重要性排序及关联关系
2.5 建立油浸式变压器质量评估模型
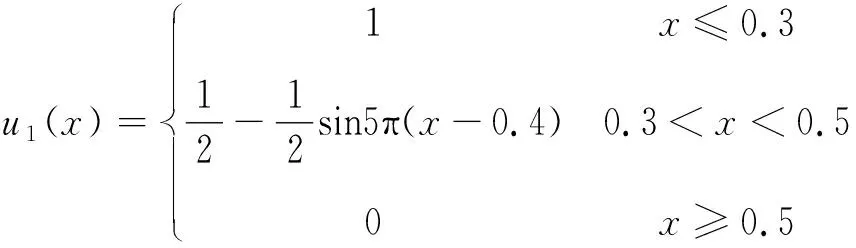

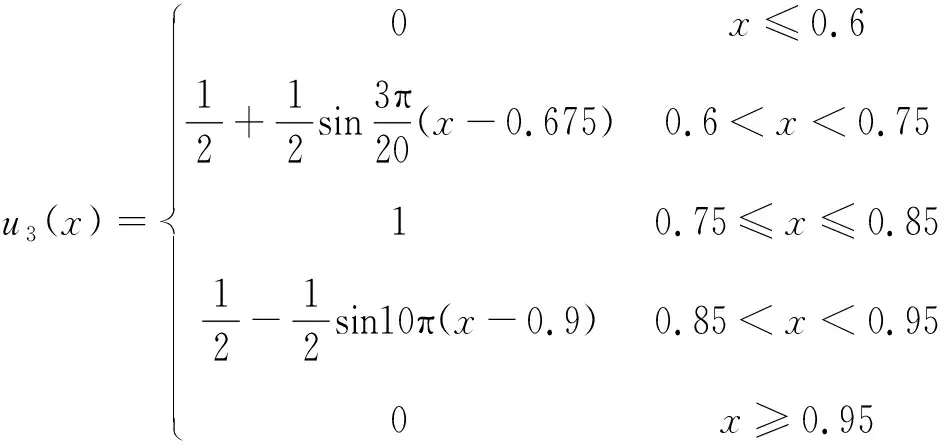
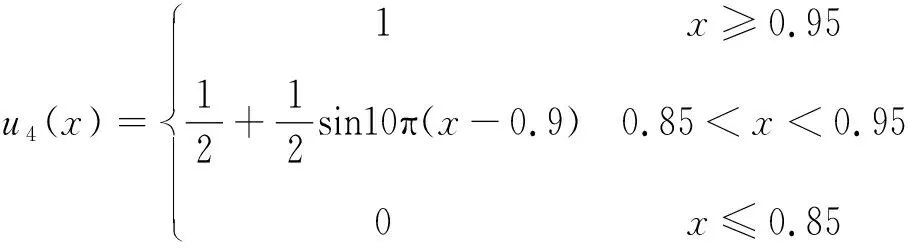

3 算例分析
3.1 综合可变权重的计算
3.2 指标重要性排序及关联关系
3.3 变压器质量等级确定

4 结论

